Data Science: About love, names and more

What does the name mean? The rose smells like a rose,

Though call it a rose, though not.



• Shakespeare "Romeo and Juliet" (trans. Pasternak)

This article can not serve as a reason for the expression of intolerance or discrimination on any grounds.

In this article I will tell you that, no matter how strange it may seem to an educated person, the probability of being lonely / alone depends on the name . That is, in fact, we will talk about love and relationships .

It is about the same as saying: the probability of being hit by a car, if your name is Seryozha, is higher than if you were called Kostya! Sounds pretty crazy, doesn't it? Well, at least, unscientific. However, social networks made it relatively easy to verify the above statement.

In detail, we will look only at girls, but let's talk about men at the very end. Moreover, I do not set my goal to establish the cause of what is happening or even put forward any serious hypothesis of any kind, but I just want to tell you about my observations and facts that can be measured.

Story

It all started with the fact that I set myself Tinder and flipped it to the end in a solid radius. That is, I looked through quite a lot of profiles of girls. After some time, I noticed that among all the names of girls, some are more common than others, but about the same amount. Specifically, it is about the names of Dasha and Ksyusha, and I have never at that time made a single swap to the right (that is, like) for girls with that name. I could somehow explain myself to myself why I paid attention to girls with the name Ksyush (for example, remembering my own experience), but I knew almost nothing about girls with the name Dasha. I also did not know much about the distribution of names, but my intuition told me that something was wrong here. The idea itself, as already noted, seemed extremely strange and unscientific to me, but I remembered it. The next time I noticed a similar result, I could not stand it anymore. I thought that either Tinder knows something that I don’t know or my assumption is not so absurd and decided to turn to statistics. I do not have access to Tinder's data, and I decided to look into the resources that are available to me - and this is Odnoklassniki (where I actually work) and open data from VKontakte.

For a start, there was at least some kind of hypothesis explaining the unevenness of the distribution of names in Tinder (adjusted for the natural frequency). I assumed that for some reason Dasha and Ksyusha are more lonely than other girls. It sounds absolutely unbelievable, and an adequate person expects that the question of loneliness, like any such indicator, is quite equally distributed among people regardless of their name, zodiac sign, and other similar nonsense. For me, the very thought of what might be different still seemed seditious, akin to homeopathy or astrology .

In Odnoklassniki, the status of a relationship can be determined by the type of relationship in the graph, and what interested me is marital and love relationships. It must be said that not very many people explicitly note the corresponding attitude. However, even the initial inspection showed that Dashis are really somewhat out of the ordinary statistics, if you enter some average value; with Ksyusha things were a little better. But my initial assessment was not very accurate. As an indicator of loneliness, I simply divided the number of women in a relationship by the number of all women with that name. But even such a simple calculation indicated that not everything was as smooth as expected.

It seemed to me that it would be nice to normalize the names in the right way, and, maybe, not to take the mean value, but simply to compare different names with each other. In addition, I really wanted to understand how this phenomenon is global and does not depend on the data source. Then I, of course, went to the VKontakte site, where there is a good search taking into account the normalization of names and you can get a sample by simply clicking on the drop-down lists, which I did.

Analysis based on VK data

To begin with, we fix a list of names, it can be arbitrary. But we will definitely take high-frequency names, such as Anastasia, Ekaterina, Elena, Maria and Natalya (more than one million, according to VC). Slightly less common, such as Daria, Alina, Ksenia and Alexandra (about 800 thousand). You also need to take something more exotic, let it be Cyrus and Inessa. Well, as a very large exotic - Leila.

Moreover, there is a known problem that the frequency of names changes, some names are always relatively popular, and some become popular in a small range of several years. To assess the impact of this issue, we consider three cases. Take the girls aged 20-35 and consider separately (interesting to me personally) the age of 28 and very young 22 years old. I deliberately did not work with the status of "civil marriage" (because it is rarely affixed) and "everything is difficult" (because its meaning is still very vague for me), well, or "engaged" (still we are not in that country we live where it has some weight), so I limited myself only to considering the most common options that act as the name of the columns in our small dataset: married , relationship , love , single and searching . We will also find how many of them are all . Each column will contain the number of girls with the desired name in this status. Of course, we must immediately make a reservation associated with the name Xenia. The fact is that Ksyushi is also called girls named Oksana, so this question requires more laborious work and we will return to it later.

Let's define how we will consider single girls. To begin with, we introduce the following first coefficient, let's call it simply v :

 v = (single + searching) / all 

those. we just take all unmarried and all those who are actively searching and share on everyone with that name. But this is only one way, you can also build an addition to those who have some kind of relationship:

 u = 1 - (married + love + relationship) / all 

thus, it is the proportion of those who are not in a relationship, and it includes the proportion that characterizes the number v .

Here I’ll act a bit unfairly, but this will reduce the size of the article in a substantial way. It turns out that it is much more interesting to consider some function q = f(v, u) or even from a larger number of parameters as an integral indicator of loneliness. For reasons of simplicity and common sense, we simply take the arithmetic average as such a function:

 q = (u + v) / 2 

It is also interesting how much girls with this name are generally inclined to write anything about their relationship - let's call this value w :

 w = (single + searching + married + love + relationship) / all 

And it would also be necessary to normalize actively seeking (this is about the same as v , only we do not take into account those who have the status of unmarried ):

 a = searching / all 

Let's see what we did.

Girls 20-35

Below is a table with calculated values ​​for VK data.

Any sensible person assumes to see approximately the same value of v and u within some small error, but not a scale from 0.125 to 0.226 for the case of v ! In the table, the rows are sorted by q (in fact, all because sorting by q gives more stable results than by v and u ). More specifically, girls named Kira are statistically significantly more lonely than girls named Natalia. Thus, the higher the value of v , u or q - the more lonely the girls with the given name.

In general, such an observation is counterintuitive, it should not be so, and one might think that we did something so wrong that the expected approximately equal values ​​of v diverged so much.

The significant difference between the top of the table and the bottom is obvious. The first thing that comes to mind is probably the distribution of names in such a large age range has some significant peaks, and they influenced the overall picture - still 15 years. That is, one would assume that if we took any one age, then the situation would be fundamentally different. Let's do this and see what happens if we take only girls 28 years old.

Girls 28 years old

')

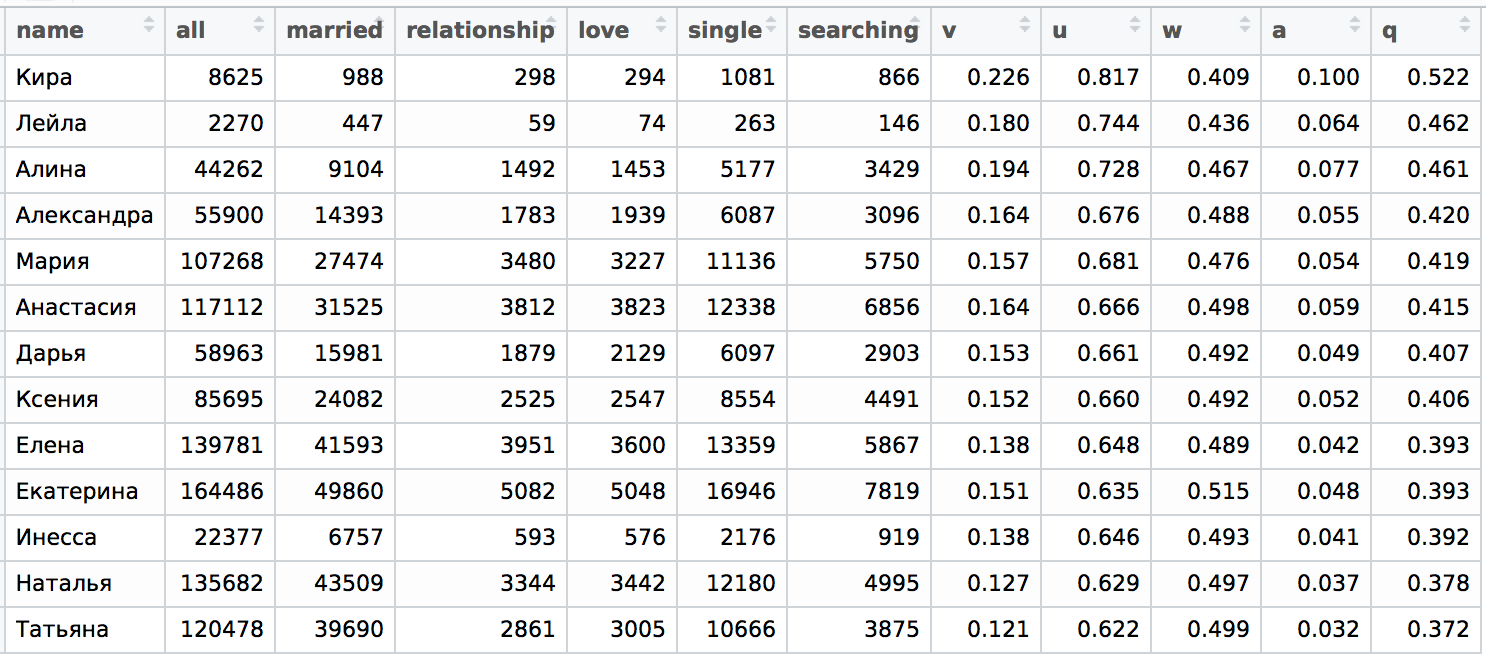
It must be said that the situation has not changed in a qualitative sense compared with a sample of 20-35 years, i.e. here we also see a significant difference between the top and bottom of the table. The structure of the upper and lower parts of the table coincides for the most part, only the middle part has changed significantly.

Thus, we can state that girls of 20-35 years old in aggregate and girls of 28 years old in a relationship behave in a similar way within their name!

Here we can hardly easily raise the question of the connection between loneliness and the frequency of a name. But there is absolutely nothing obvious here. In the following sections, we denormalize the names and consider this issue in more detail.

Well, this is a girl of 28 years, i.e. about the average age in our initial range, you say! And what actually happens to younger people, well, let's say, at 22? Let's get a look.

Very young persons of 22 years

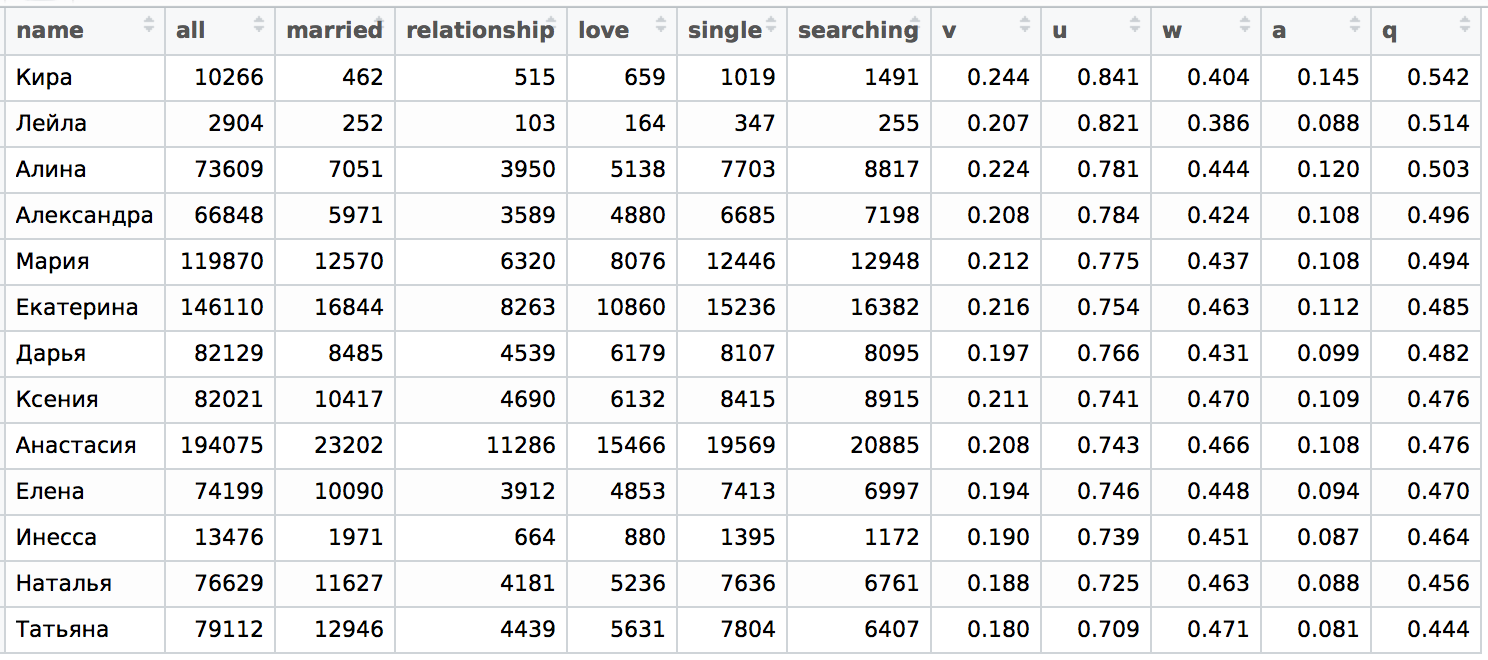
Now this is more interesting, here everything is the same, that in the case of 28 years old, Catherine and Anastasia just changed places. The rest of the table structure turned out to be the same (I remind you, we sort by q ).

Statistics by region

The next thing to check is what happens to the regions. Suddenly everything is different there? In this case, some kind of compromise was needed due to the fact that there are rare names, and I preferred to make a calculation for ages 20-35 in order to have enough data.

Let's start with St. Petersburg:

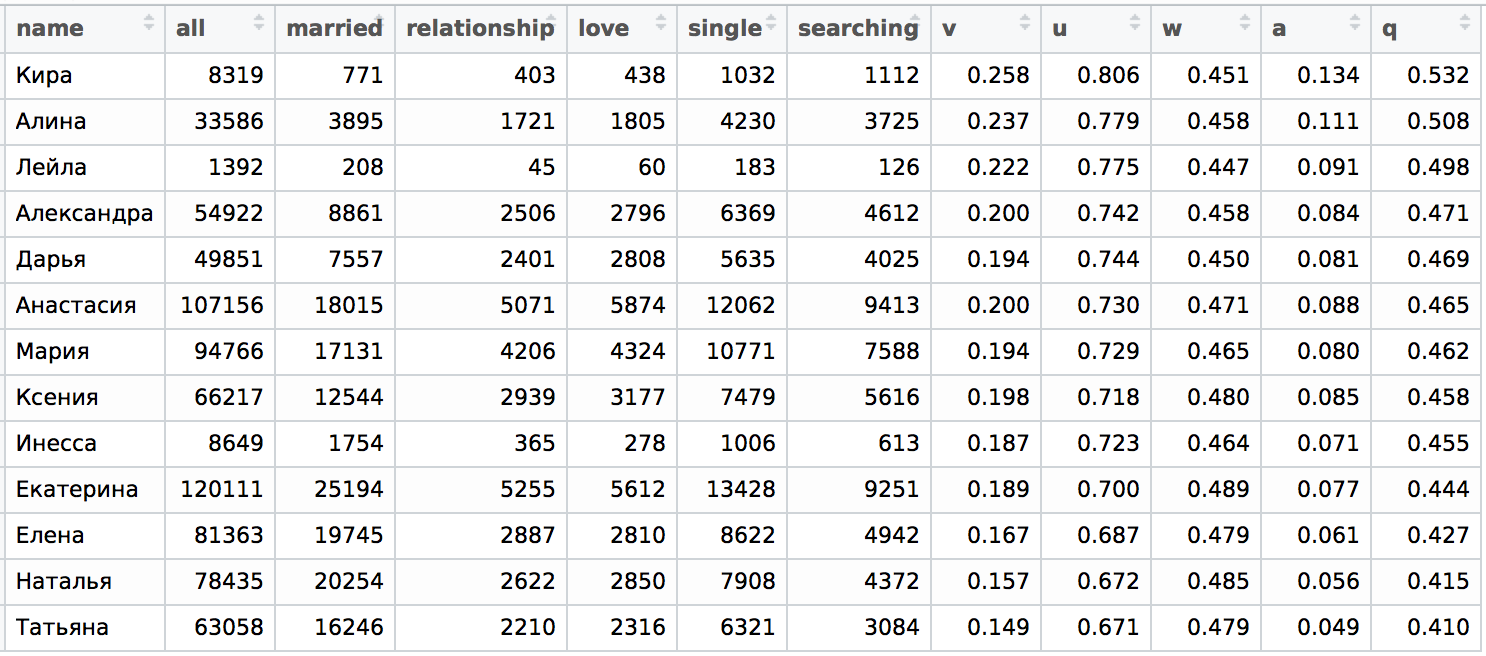
As might be expected, the situation in Moscow is very similar with one significant exception - girls named Inessa are much more lonely than girls named Anastasia, whereas in St. Petersburg the situation is exactly the opposite:

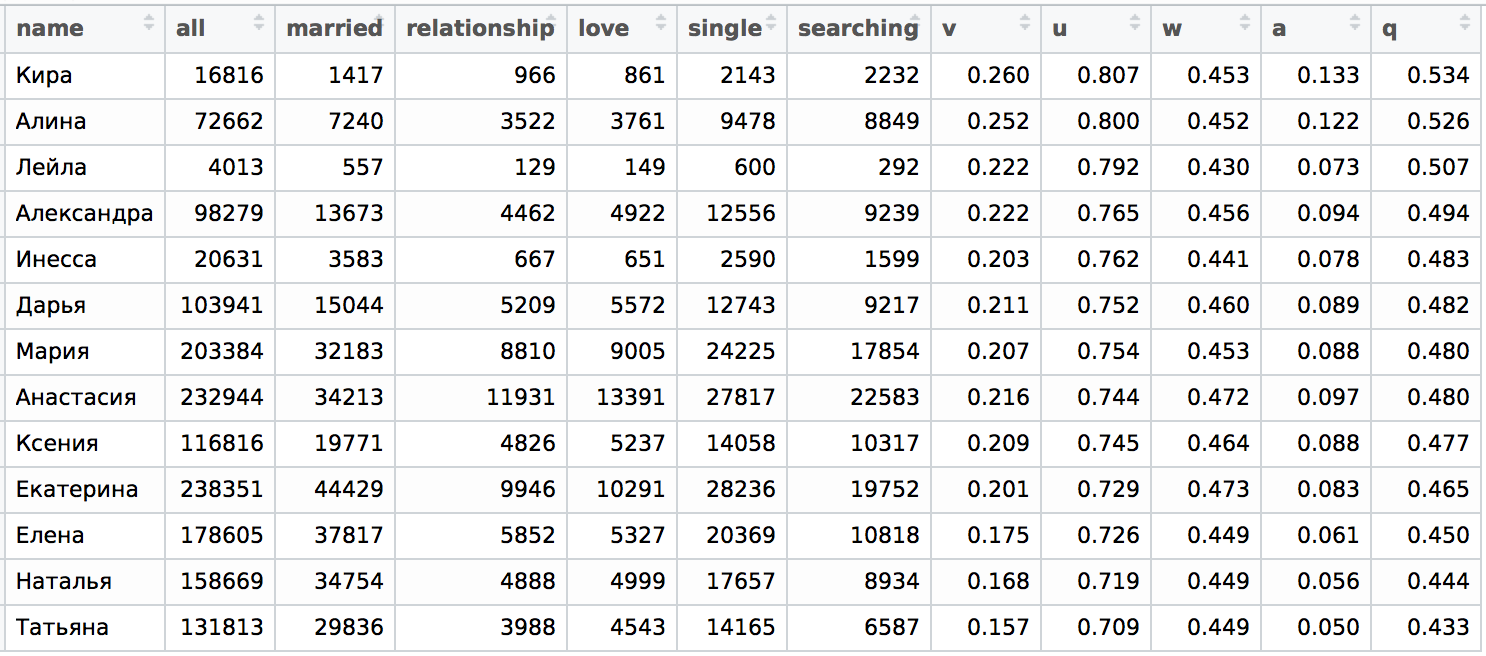
Now look at the Urals in the city of Yekaterinburg. As you can see, the upper and lower parts also coincide with Moscow, and, if you swap Mary and Inessa, it will be just the same:

Finally, we look at Novosibirsk. Moreover, if, as we have already seen, Yekaterinburg is more like Moscow, then Novosibirsk is about St. Petersburg, also with slight differences. Unfortunately, there is clearly not enough statistics by the name of Leyla, but now we will not pay attention to this, it is enough for us to have a qualitative picture:

Here, probably, everything, we made sure that the general structure of the tables is preserved with small changes depending on the regions. Thus, we can say that the distribution of names in terms of loneliness does not depend significantly on age and region . You need to make a reservation about the region - the cities are chosen so that there are no significant cultural or religious differences between them.

Everything would be great, but I would like to have another source that confirms or denies the appropriate distribution.

Analysis based on Odnoklassniki data

In this case, take a sample of about 10 million users and try to calculate for it what we did for the VC case. On the one hand, we will take less (but enough data), on the other hand, for this data we can count a lot more. As I mentioned, the process of setting the status of relationships in OC is fundamentally different, and there will be less data here, so only the status of marriage and love relationships is taken into account here. Truth be told, approximately 80% of statuses are accounted for by marriage.

We were convinced that we can safely use the sample for 20-35 years as a representative one, because it is almost indistinguishable from the slice for a specific age and does not significantly depend on the region. For all tables, we take only users who have more than 15 friends, although this does not have any significant effect on the order of names after sorting, but it is essential for calculating the number of friends "on average".

To begin, let us try to understand whether the sort order will coincide in case of normalization of names. Then, with the help of a more detailed analysis, we will divide the girls with the name Xenia and Oksana, and also see what happens with the diminutive forms of names.

Normalized and unnormalized names

The first table presents the normalized case, but we are not doing the normalization Oksana -> Xenia, but looking ahead a bit, I can say that this is not necessary.

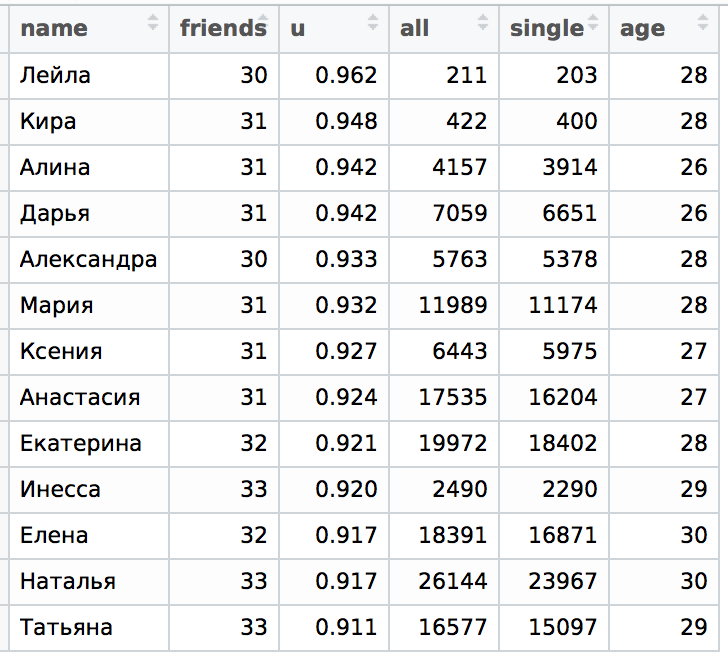
The overall structure of the table corresponds to the data from the VC with minor changes. The value of u here is an analogue of our u of the VC data (this value is always great, because far fewer people put status in relations in the OC). Moreover, here it is convenient for us to calculate the value of age “on average” in a group and the number of friends “on average”. It is possible that the average age value affects the sorting, for example, if the lower part of the table is older. Then the number of singles should be less. But you and I just know, according to the VC, that the sections for the same age are about the same. In fact, the data that we saw is clearly not enough. I would like to make sure that the average age in the group and the frequency of the name do not have a strong effect.

Moreover, even with different mechanics of setting the status - the distribution is the same. In fact, it was easy to round up to the second digit, but the essence does not change, because we understand that you can move the names inside a part of the table, without changing the qualitative assessment, and that is what is important to us in the first place.

To do this, let's add a few low-frequency names, for example, Lia and Asya (very rare), Snezhana, Angela, Diana and Lily (just low-frequency), as well as several missing high-frequency (Anna, Olga) and denormalize names (but diminutive versions do not we will), thus dividing the girls named Ksenia and Oksana, as well as Inessa and Inna, although the latter is often used as an abbreviated version for Inessa:

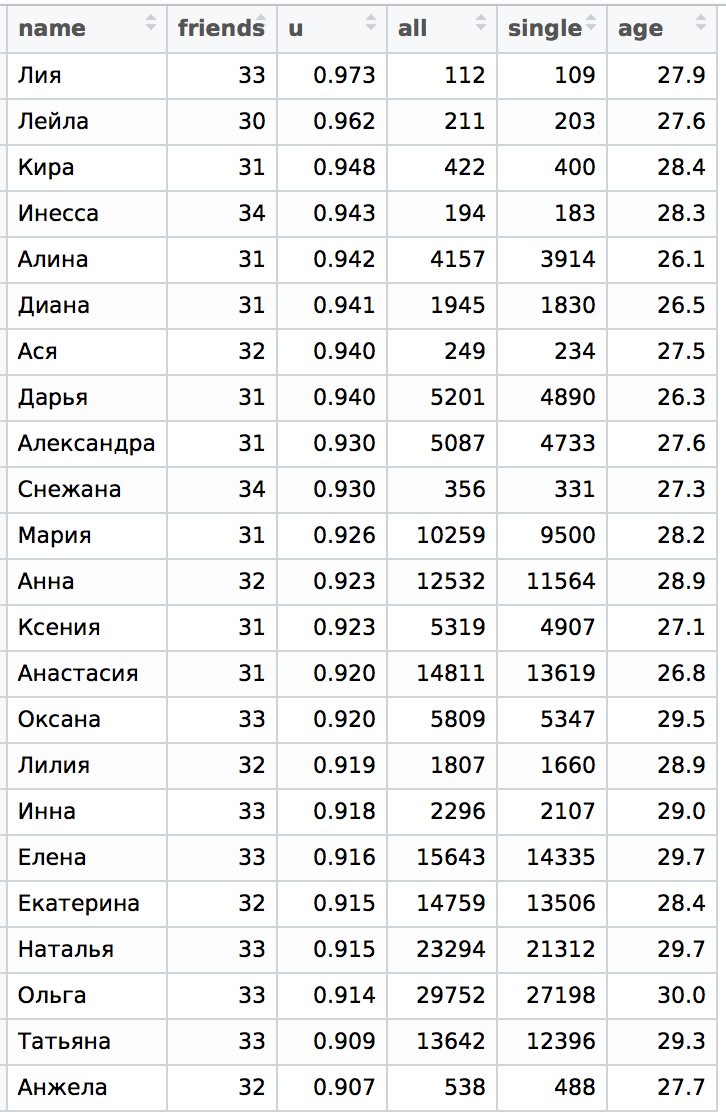
It can be seen that the names Xenia and Oksana behave about the same, being very close to the table. But with the names of Inna and Inessa everything is different. Despite the fact that the name Inna is often used instead of the name Inessa and vice versa (which spoils the statistics for normalized names), the statistics for these names are completely different. Inna is still a completely different name and in order to see it in detail we ask ourselves what will happen to the diminutive names and what our table will look like.

Pet names

Let's take a look at our first tablet in this section. I added one or several variants of diminutive names to the main list (without Snezhana, Angela and others). The resulting picture is very interesting:

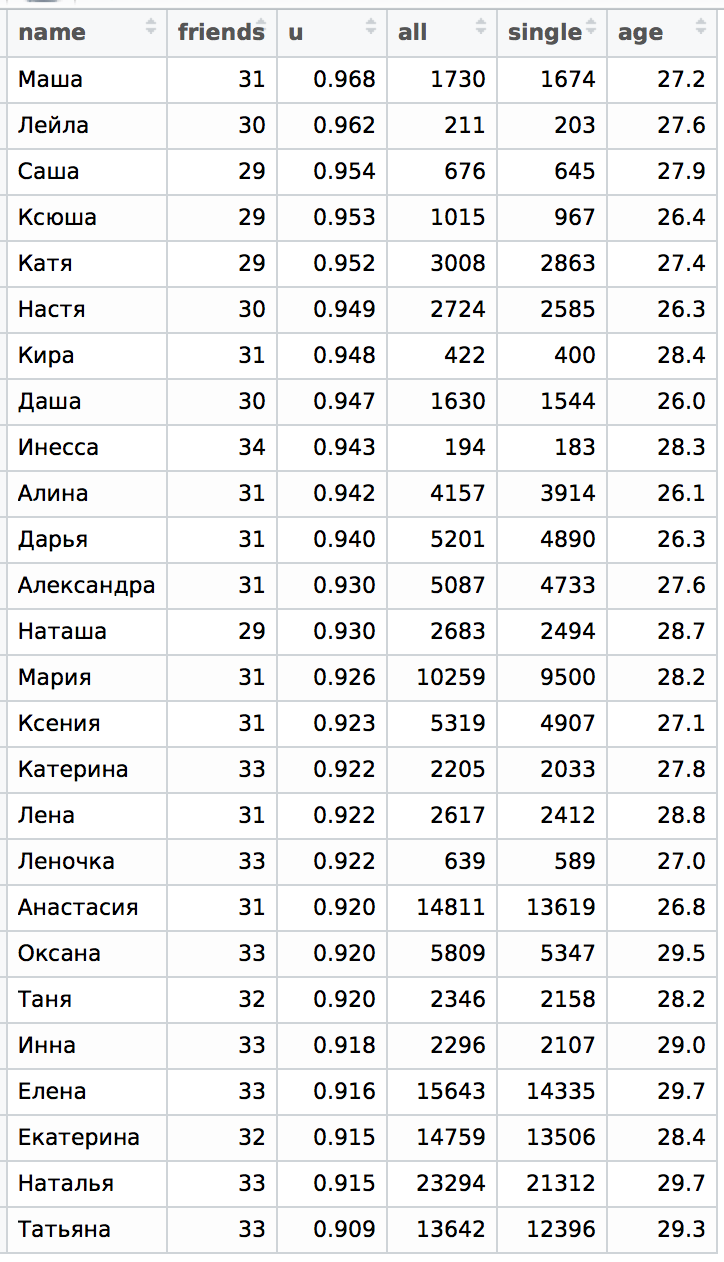
It is immediately obvious that girls with diminutive names are always more alone, except in the case of Inna / Inessa . Actually it was expected that this pair should behave in a fundamentally different way. From our previous experience, we know that the names Xenia and Oksana behave the same way, so it doesn’t matter to us where to put the name Ksyusha. The names Elena and Daria are closest to their diminutive variants, all the rest are very far away, especially Catherine and Maria. In addition, it is clear that Masha, Sasha, Ksyusha and Katya were at the very top of the table.

In addition to the qualitative assessment of this issue, something more specific cannot be said. But in this case, you can at least make some reasonable hypothesis about the origin of this problem. There are two main options:

• Perhaps the fact is that girls with a diminutive version of the name are simply younger, and the likelihood of entering into a relationship depends only on the full form of the name. Indeed, it is clear that with the diminutive names of the girl "on average" younger than a year.

  
  
  
• The second option is also interesting, it is possible that it is those who are already married who set themselves a full, not a diminutive, name. Or, on the contrary, single girls prefer short versions of their name.

It is hard enough to test the second hypothesis, but you can test the first one. To do this, we need to expand our little dataset, adding to it the average age for those who are exactly married. If the difference between the average age and the average age in marriage will differ greatly for the variants of the name, this will speak in favor of the first hypothesis. But it should be understood that the hypotheses are not mutually exclusive; rather, the second one can "include" the first one.

It is also clear from the previous table that the number of friends "on average" is approximately the same and does not provide any additional information on the move.

In the new table, the fields friend_ns and age_ns are the corresponding "average" values ​​for the case of married girls.

We also introduce several synthetic fields:

 delta_f = friends_ns - friends delta_a = age_ns - age 

which show the difference in performance in the case of married and corresponding values ​​"on average". We will talk about the correct interpretation of the expression "on average" in the section "Technical Details".

For non-single girls, the situation with friends "on average" is completely different, you can see a significant variation in values, as the delta_f field delta_f . In fact, this may serve as an indirect confirmation of the hypothesis proposed by Chris Radder . He writes that the strength of a marriage is measured by the degree of assimilation of each spouse into the other’s network of connections . That is, a significant change in the number of friends "on average" is associated with the assimilation of the social graph of the husband / partner.

But let us return to our hypotheses so far: as you can see, the larger the delta_a absolute value for a short name compared to the full name, the higher the short name in the table (at least qualitatively), which to some extent confirms our first hypothesis about influence of age "on average".

And so far, nothing but intuition and common sense, does not indicate a second hypothesis.

Technical details

To begin with, we certainly do not always have enough data, as can be seen from the tables. But a qualitative assessment is still available to us. I didn’t really like to bother myself and you with detailed calculations, because the situation is already quite on the surface.

But you have to be decent people and talk a little about rounding (I already said that in the case of OK, you can safely round to the second digit) and the average value.

Values ​​"on average"

Before, everywhere I used the expression "on average" only in quotes. Consider for example the age, which in some tables I rounded up to the first character, so that you can see it better. Can we talk here about the average value? On the one hand, there are no emissions, but hardly anyone would expect that age will always be distributed normally. However, if you take all the same names Oksana and Ksenia, who behave in a similar way and have the same short form - Ksyusha, you can see that Oksana is “on average” older than Ksyusha. This is due to the changing popularity of the name. Let's take a look at the chart for some names.

These charts do not sufficiently reflect the global distribution of names by age. To do this, they should be normalized, taking into account the age distribution in the social network, which we will not do here, we are more interested in the local picture. Here are some more charts for other names:

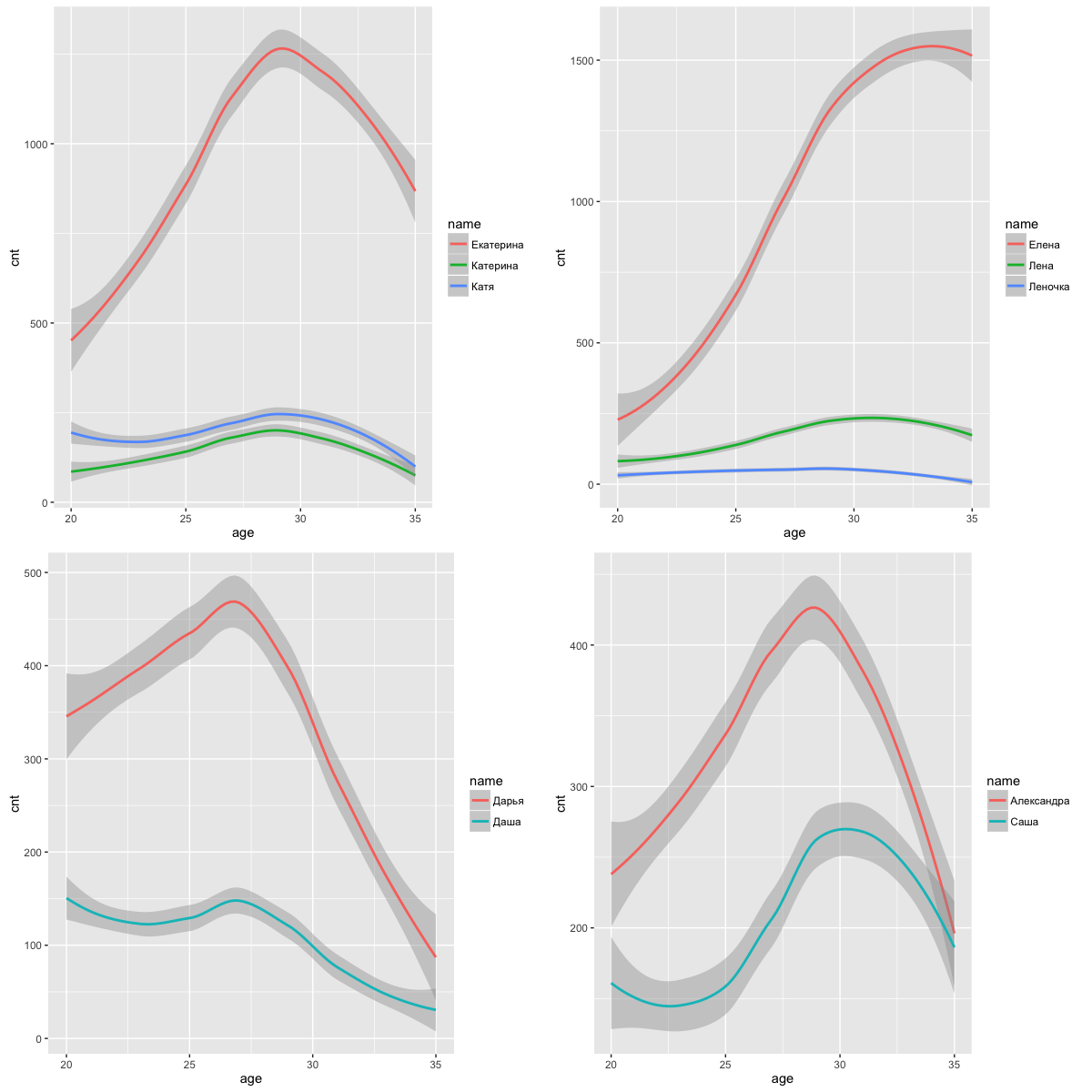
However, we cannot expect a distribution without strong outliers in the case of the number of friends, therefore the median will be suitable as “on average”.

Error

I rounded in tables from the VC to the third digit of the value for q . How correct is it? For verification, I took the measurement again, but after a week and a half. The result is presented in the following table:

As you can see, comparing with the first table, not only the sorting coincides, but also the value of q , except for the case with the name Daria. As it turned out, for some reason, the VC in the search sometimes shows a smaller number, in the absence of filters. This time I noticed it, because I started with Darya (as in the past) and the total number of girls with that name turned out to be even slightly less than last time. So I made some more measurements. Thus, there is reason to believe that the value for this name in the last table is more reliable, although the overall picture is fully preserved for the previous measurement.

Since, first of all, it is important for us to have a qualitative assessment of the situation, there is not much point in doing the same with the data from OK and, to save time and space, we will omit it.

Dry residue and conclusion

What have we learned? Despite the absolute improbability of the idea itself, the uneven distribution depending on the name can be confirmed; moreover, the distribution of names does not depend on the frequency of the name, the region (within reasonable limits) or the source of the data. If it’s completely dry: the name is a feature .

I will not try here to build a model or put forward hypotheses that would somehow describe the results obtained. However, I note that the data obtained for the name Leyla and Lia are quite expected. Because the first name of "Arabic origin" and girls with that name probably are carriers of a cultural tradition that differs from the cultural tradition of girls with "more traditional Russian names." And the name Lia "is very widespread among Jews" and probably also carries some cultural characteristics.

But, in general, I still cannot offer any arbitrarily well-grounded theory that could explain the observed results.

You can even make various corrections to the fact that not everyone has the status set and set correctly (true to reality), but in any case, reasoning leads to the fact that the differences are related to the behavioral features of the name. Thus, in the worst case, we have the following conclusion: depending on the name, girls behave differently .

It would be very interesting to receive feedback from sociologists, psychologists and onomastic specialists in this matter.

.

, : , , , .

, , . 20-35 .

q , " ", v , , q .

w a , .

, - . , , .