Reed-Solomon codes. Part 1 - the theory of simple language
Good day! My name is Maxim, in YADRO, among other things, I am developing a subsystem that is responsible for reliable data storage. I am preparing a small cycle of articles about Reed-Solomon codes - a theoretical basis, a practical implementation, software and hardware optimizations used in practice. On Habré and the rest of the network there are good articles on issues in this area - but it’s hard to figure out if you are new to the topic. In this article I will try to give a clear introduction to the Reed-Solomon codes, and in the next issues I will write how to program all this.

One of the main areas of work of the company YADRO is the development of data storage systems (DSS). You can discuss for a long time which characteristics of these systems are the most important from the end user's point of view. This may be the speed of I / O operations, the cost of owning the system, the level of power consumption or something else. But all these characteristics will make sense only if the system provides the necessary level of data integrity for the user. As a result, for all developers of such systems, the issues of ensuring the reliability of data storage come to the fore.
For a long time, RAID remained the main player in the field of secure data storage. Such classical solutions, along with well-known advantages, have certain limitations. These include:
In this regard, in recent times, technologies based on all sorts of redundant codes are gaining popularity (in the English-language literature, the name of this technology has been fixed - erasure coding), which provide much more opportunities than classic RAID.
')
At the moment, our team is developing a storage system TATLIN . According to the system architecture, we plan to write a separate series of articles, here we just say that at some point in time we were faced with the task of implementing our own system of reliable data storage. After studying the issue, we decided to dwell on the time-tested Reed-Solomon codes. There are ready-made libraries (for example, ISA-L from Intel or Jerasure by James S. Plank). They implement the corresponding encoding / decoding procedures. But considering that our hardware platform is based on the OpenPOWER architecture, and the entire system logic is implemented as a Linux kernel module, it was decided to make our own implementation optimized for the particularities of our system.
In this first article I will try to explain what is at stake when they talk about Reed-Solomon codes in the context of data storage systems. Let's start with simple examples that will allow you to better understand the essence of the problems to be solved.
Suppose there are two arbitrary integers and . It is necessary to develop an algorithm that will assign the third number to these two numbers , moreover, such that it will be possible to unambiguously restore any of the two original numbers if one of them is lost. In other words, having a couple ( and ) or ( and ), it is possible to unambiguously restore or respectively. There are many options for implementing such an algorithm, but probably the simplest is the one that applies the “exclusive OR” (XOR) bit operation to the two source numbers, i.e. . Then to recover you can use equality (recovery , ).
Let's complicate the task a bit. Suppose that the original numbers are not two, but three , and . As before, we need an algorithm to cope with the loss of one of the original numbers. It is easy to notice that nothing prevents the use of the bit operation “Exclusive“ OR ”, . Recovery you can use equality .
Let's complicate the task a little more. As before, there are three numbers , and , but to lose, this time, we can not one, but any two of them. Obviously, simply using the “Exclusive“ OR ”operation will no longer work. How to recover lost numbers?
One of the possible ways to solve this problem is the use of Reed-Solomon codes. The formal description of the method is easy to find on the Internet, but the main problem is that for people far from the “Galois fields” it is quite difficult to understand how it all works. For example, the definition from Wikipedia :

Let's try to figure out how it works, starting with more intuitive things. To do this, go back to our last task. Recall that there are three arbitrary integers, any two of them can be lost, you need to learn how to recover the lost numbers for the remaining ones. To do this, apply the "algebraic" approach.
But before it is necessary to remind one more important point. Data recovery technologies are not without reason called overcoding methods. Based on the initial data, some “redundant” are calculated, which then allow you to recover lost ones. Without going into details, we note that the rule of thumb is that the more data can be lost, the more “redundant” it is necessary to have. In our case, to recover two numbers, we have to construct two “redundant” ones using some algorithm. In general, if you need to maintain a loss numbers, you must respectively have redundant.
The “algebraic” approach mentioned above is as follows. A matrix of special size is made up. . The first three rows of this matrix form a unit matrix, and the last two are some numbers, the choice of which we will discuss later. In the English-language literature, this matrix is usually called the generator matrix , in the Russian language there are several names, in this article the generating matrix will be used. Multiply the constructed matrix by a vector composed of the original numbers. , and .

As a result of multiplying the matrix by the vector with the data, we obtain two “redundant” numbers, denoted in the figure as and . Let's see how using this “redundant” data you can recover, for example, lost and .
We delete the rows corresponding to the “missing” data from the generator matrix. In our case matches the first line, but - the second. The resulting matrix is multiplied by the vector with the data, and as a result we get the following equation:
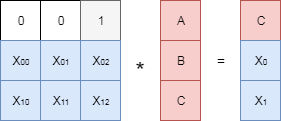
The only problem is that and we have lost, and they are now unknown to us. How can we find them? There is a very elegant solution to this problem.
We delete the corresponding rows from the generating matrix and find the inverse of it. In the figure, this inverse matrix is denoted as . Now we multiply the left and right sides of the original equation by this inverse matrix:

By shortening the matrices on the left side of the equation (the product of the inverse and direct matrices is the identity matrix), and taking into account the fact that there are no unknown parameters on the right side of the equation, we get the expressions for the desired and .
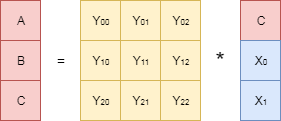
Strictly speaking, what we have just done is the basis of all types of Reed-Solomon codes used in data storage systems. The coding process is to find “redundant” data , , and the decoding process is in finding the inverse matrix and multiplying it by the vector of the “preserved” data.
It is easy to see that the considered scheme can be generalized to an arbitrary amount of “source” and “redundant” data. In other words, by source numbers can be built redundant, and it is always possible to recover the loss of any of numbers In this case, the generator matrix will have a size , and the top of the matrix size will be single.
Let us return to the question of constructing a generating matrix. Can we choose numbers arbitrarily? The answer is no. They should be chosen in such a way that regardless of the lines crossed out, the matrix remains reversible. Fortunately, in mathematics, the types of matrices that possess the necessary property are well known. For example, the Cauchy matrix . In this case, the coding method itself is often called the Cauchy-Reed-Solomon method (Cauchy-Reed-Solomon). Sometimes, the Vandermond matrix is used for the same purpose, and accordingly, the method is called Vandermonde-Reed-Solomon.
Go to the next problem. A computer uses a fixed number of bytes to represent numbers. Accordingly, in our algorithms we cannot freely operate with arbitrary rational, and even more so, real numbers. We simply can not implement such an algorithm on a computer. In our case, the generating matrix consists of integers, but when this matrix is inverted, rational numbers may arise, which are problematic to represent in computer memory. So we got to the place where the famous Galois fields come on the scene.
So what are the Galois fields? Let's start again with explanatory examples. We are all accustomed to operate (add, subtract, multiply, divide, etc.) with numbers - natural, rational, real. However, instead of the usual numbers, we can begin to consider arbitrary sets of objects (finite and / or infinite) and enter operations similar to addition, subtraction, etc. on these sets. As a matter of fact, mathematical structures of the type of groups, rings, fields are sets on which certain operations are introduced, and the results of these operations belong to the original set again. For example, on the set of natural numbers, we can introduce standard operations of addition, subtraction and multiplication. The result will again be a natural number. But with the division everything is worse; when dividing two natural numbers, the result can be a fractional number.
A field is a set on which operations of addition, subtraction, multiplication and division are specified. An example is the field of rational numbers (fractions). A Galois field is a finite field (a set containing a finite number of elements). Usually Galois fields are denoted as where - the number of elements in the field. Developed methods for constructing fields of the required dimension (if possible). The end result of such constructions is usually the addition and multiplication tables, which the third field element assigns to the two field elements.
The question may arise - how are we going to use all this? When implementing algorithms on a computer, it is convenient to work with bytes. Our algorithm can take on input bytes of source data and calculate them bytes are redundant. One byte can contain 256 different values, therefore, we can create a field and count the excess bytes, using Galois field arithmetic. The approach to encoding / decoding data (building a generator matrix, matrix inversion, matrix multiplication by a column) remains the same as before.
Well, we finally learned from the original bytes construct additional bytes that can be used in case of failures. How does all this work in real storage systems? In real storage, they usually work with fixed-size data blocks (in different systems, this size varies from tens of megabytes to gigabytes). This fixed block is broken into fragments and on them are constructed additional fragments.
The process of constructing fragments is as follows. Take one byte from each of source fragments at offset 0. According to this data, K additional bytes are generated, each of which goes to the corresponding additional fragments at offset 0. This process is repeated to offset - 1, 2, 3, ... After the encoding procedure is completed, the fragments are stored on different drives. This can be represented as follows:

If one or more disks fail, the corresponding lost fragments are reconstructed and stored on other disks.
The theoretical part is gradually coming to an end, let's hope that the basic principle of encoding and decoding data using Reed-Solomon codes is now more or less clear. If there is interest in this topic, then in the following parts it will be possible to dwell in greater detail on the Galith field arithmetic, implementations of the encoding / decoding algorithm on specific hardware platforms, to talk about optimization techniques.
UPD . List of references on the topic ( comments whitedruid thanks):
- “Algebraic coding theory”, Berlekamp E., 1971.
- "Theory of Error Correction Codes", McWilliams, F., Sloan NJ, 1979.
- "Theory and practice of codes that control errors.", 1986.
- “The art of noiseproof coding. Methods, algorithms, application ”, Morelos-Zaragoza R., 2005.
- “Error Correction Coding in Digital Communication Systems”, Clark J., Kane J., 1987.
- “Packing of balls, lattices and groups.”, Conway J.N., Sloan N.J.A., 1990.
whitedruid : I read the book “Packing balls, lattices and groups” relatively recently - I liked it a lot!
- “ Introduction to Algebraic Codes ” - lectures by MIPT teacher Yury L'vovich Sagalovich, designed in the form of a book.
- “ Reed-Solomon codes from the point of view of the average man ” - is written in simple language.
- “ Error Correction Codes ” - briefly, clearly and with pictures :)
- “ Notes on coding theory ”, A. Romashchenko, A. Rumyantsev, A. Shen, 2011. - a kind of "cheat sheet" - briefly, succinctly, but requires a certain level of preparation .
- You also can not ignore the seminars on "Coding Theory" , which are regularly organized by the staff of the Institute for Information Transmission Problems. A.A. Kharkevich, Russian Academy of Sciences, Moscow. Further - on the links - you can find a lot of interesting things on topics related to the mathematical theory of coding, relevant issues are raised within the discipline. For example, about sequential decoding of polar and extended Reed-Solomon codes . In the search engines you can already find articles by the author.

Why we deal with Reed-Solomon codes
One of the main areas of work of the company YADRO is the development of data storage systems (DSS). You can discuss for a long time which characteristics of these systems are the most important from the end user's point of view. This may be the speed of I / O operations, the cost of owning the system, the level of power consumption or something else. But all these characteristics will make sense only if the system provides the necessary level of data integrity for the user. As a result, for all developers of such systems, the issues of ensuring the reliability of data storage come to the fore.
For a long time, RAID remained the main player in the field of secure data storage. Such classical solutions, along with well-known advantages, have certain limitations. These include:
- relatively low level of protection (for example, RAID 6 can fail a maximum of two drives)
- need to keep spare discs
- inability to control the distribution of “parity” blocks (this may be important for certain types of disks)
- difficulty supporting heterogeneous disks
In this regard, in recent times, technologies based on all sorts of redundant codes are gaining popularity (in the English-language literature, the name of this technology has been fixed - erasure coding), which provide much more opportunities than classic RAID.
')
At the moment, our team is developing a storage system TATLIN . According to the system architecture, we plan to write a separate series of articles, here we just say that at some point in time we were faced with the task of implementing our own system of reliable data storage. After studying the issue, we decided to dwell on the time-tested Reed-Solomon codes. There are ready-made libraries (for example, ISA-L from Intel or Jerasure by James S. Plank). They implement the corresponding encoding / decoding procedures. But considering that our hardware platform is based on the OpenPOWER architecture, and the entire system logic is implemented as a Linux kernel module, it was decided to make our own implementation optimized for the particularities of our system.
In this first article I will try to explain what is at stake when they talk about Reed-Solomon codes in the context of data storage systems. Let's start with simple examples that will allow you to better understand the essence of the problems to be solved.
The basic task of restoring lost
Suppose there are two arbitrary integers and . It is necessary to develop an algorithm that will assign the third number to these two numbers , moreover, such that it will be possible to unambiguously restore any of the two original numbers if one of them is lost. In other words, having a couple ( and ) or ( and ), it is possible to unambiguously restore or respectively. There are many options for implementing such an algorithm, but probably the simplest is the one that applies the “exclusive OR” (XOR) bit operation to the two source numbers, i.e. . Then to recover you can use equality (recovery , ).
Let's complicate the task a bit. Suppose that the original numbers are not two, but three , and . As before, we need an algorithm to cope with the loss of one of the original numbers. It is easy to notice that nothing prevents the use of the bit operation “Exclusive“ OR ”, . Recovery you can use equality .
Let's complicate the task a little more. As before, there are three numbers , and , but to lose, this time, we can not one, but any two of them. Obviously, simply using the “Exclusive“ OR ”operation will no longer work. How to recover lost numbers?
Reed-Solomon coding principle on simple examples with pictures
One of the possible ways to solve this problem is the use of Reed-Solomon codes. The formal description of the method is easy to find on the Internet, but the main problem is that for people far from the “Galois fields” it is quite difficult to understand how it all works. For example, the definition from Wikipedia :

Let's try to figure out how it works, starting with more intuitive things. To do this, go back to our last task. Recall that there are three arbitrary integers, any two of them can be lost, you need to learn how to recover the lost numbers for the remaining ones. To do this, apply the "algebraic" approach.
But before it is necessary to remind one more important point. Data recovery technologies are not without reason called overcoding methods. Based on the initial data, some “redundant” are calculated, which then allow you to recover lost ones. Without going into details, we note that the rule of thumb is that the more data can be lost, the more “redundant” it is necessary to have. In our case, to recover two numbers, we have to construct two “redundant” ones using some algorithm. In general, if you need to maintain a loss numbers, you must respectively have redundant.
The “algebraic” approach mentioned above is as follows. A matrix of special size is made up. . The first three rows of this matrix form a unit matrix, and the last two are some numbers, the choice of which we will discuss later. In the English-language literature, this matrix is usually called the generator matrix , in the Russian language there are several names, in this article the generating matrix will be used. Multiply the constructed matrix by a vector composed of the original numbers. , and .

As a result of multiplying the matrix by the vector with the data, we obtain two “redundant” numbers, denoted in the figure as and . Let's see how using this “redundant” data you can recover, for example, lost and .
We delete the rows corresponding to the “missing” data from the generator matrix. In our case matches the first line, but - the second. The resulting matrix is multiplied by the vector with the data, and as a result we get the following equation:

The only problem is that and we have lost, and they are now unknown to us. How can we find them? There is a very elegant solution to this problem.
We delete the corresponding rows from the generating matrix and find the inverse of it. In the figure, this inverse matrix is denoted as . Now we multiply the left and right sides of the original equation by this inverse matrix:

By shortening the matrices on the left side of the equation (the product of the inverse and direct matrices is the identity matrix), and taking into account the fact that there are no unknown parameters on the right side of the equation, we get the expressions for the desired and .

Strictly speaking, what we have just done is the basis of all types of Reed-Solomon codes used in data storage systems. The coding process is to find “redundant” data , , and the decoding process is in finding the inverse matrix and multiplying it by the vector of the “preserved” data.
It is easy to see that the considered scheme can be generalized to an arbitrary amount of “source” and “redundant” data. In other words, by source numbers can be built redundant, and it is always possible to recover the loss of any of numbers In this case, the generator matrix will have a size , and the top of the matrix size will be single.
Let us return to the question of constructing a generating matrix. Can we choose numbers arbitrarily? The answer is no. They should be chosen in such a way that regardless of the lines crossed out, the matrix remains reversible. Fortunately, in mathematics, the types of matrices that possess the necessary property are well known. For example, the Cauchy matrix . In this case, the coding method itself is often called the Cauchy-Reed-Solomon method (Cauchy-Reed-Solomon). Sometimes, the Vandermond matrix is used for the same purpose, and accordingly, the method is called Vandermonde-Reed-Solomon.
Go to the next problem. A computer uses a fixed number of bytes to represent numbers. Accordingly, in our algorithms we cannot freely operate with arbitrary rational, and even more so, real numbers. We simply can not implement such an algorithm on a computer. In our case, the generating matrix consists of integers, but when this matrix is inverted, rational numbers may arise, which are problematic to represent in computer memory. So we got to the place where the famous Galois fields come on the scene.
Paul Galois
So what are the Galois fields? Let's start again with explanatory examples. We are all accustomed to operate (add, subtract, multiply, divide, etc.) with numbers - natural, rational, real. However, instead of the usual numbers, we can begin to consider arbitrary sets of objects (finite and / or infinite) and enter operations similar to addition, subtraction, etc. on these sets. As a matter of fact, mathematical structures of the type of groups, rings, fields are sets on which certain operations are introduced, and the results of these operations belong to the original set again. For example, on the set of natural numbers, we can introduce standard operations of addition, subtraction and multiplication. The result will again be a natural number. But with the division everything is worse; when dividing two natural numbers, the result can be a fractional number.
A field is a set on which operations of addition, subtraction, multiplication and division are specified. An example is the field of rational numbers (fractions). A Galois field is a finite field (a set containing a finite number of elements). Usually Galois fields are denoted as where - the number of elements in the field. Developed methods for constructing fields of the required dimension (if possible). The end result of such constructions is usually the addition and multiplication tables, which the third field element assigns to the two field elements.
The question may arise - how are we going to use all this? When implementing algorithms on a computer, it is convenient to work with bytes. Our algorithm can take on input bytes of source data and calculate them bytes are redundant. One byte can contain 256 different values, therefore, we can create a field and count the excess bytes, using Galois field arithmetic. The approach to encoding / decoding data (building a generator matrix, matrix inversion, matrix multiplication by a column) remains the same as before.
Well, we finally learned from the original bytes construct additional bytes that can be used in case of failures. How does all this work in real storage systems? In real storage, they usually work with fixed-size data blocks (in different systems, this size varies from tens of megabytes to gigabytes). This fixed block is broken into fragments and on them are constructed additional fragments.
The process of constructing fragments is as follows. Take one byte from each of source fragments at offset 0. According to this data, K additional bytes are generated, each of which goes to the corresponding additional fragments at offset 0. This process is repeated to offset - 1, 2, 3, ... After the encoding procedure is completed, the fragments are stored on different drives. This can be represented as follows:

If one or more disks fail, the corresponding lost fragments are reconstructed and stored on other disks.
The theoretical part is gradually coming to an end, let's hope that the basic principle of encoding and decoding data using Reed-Solomon codes is now more or less clear. If there is interest in this topic, then in the following parts it will be possible to dwell in greater detail on the Galith field arithmetic, implementations of the encoding / decoding algorithm on specific hardware platforms, to talk about optimization techniques.
UPD . List of references on the topic ( comments whitedruid thanks):
- “Algebraic coding theory”, Berlekamp E., 1971.
- "Theory of Error Correction Codes", McWilliams, F., Sloan NJ, 1979.
- "Theory and practice of codes that control errors.", 1986.
- “The art of noiseproof coding. Methods, algorithms, application ”, Morelos-Zaragoza R., 2005.
- “Error Correction Coding in Digital Communication Systems”, Clark J., Kane J., 1987.
- “Packing of balls, lattices and groups.”, Conway J.N., Sloan N.J.A., 1990.
whitedruid : I read the book “Packing balls, lattices and groups” relatively recently - I liked it a lot!
- “ Introduction to Algebraic Codes ” - lectures by MIPT teacher Yury L'vovich Sagalovich, designed in the form of a book.
- “ Reed-Solomon codes from the point of view of the average man ” - is written in simple language.
- “ Error Correction Codes ” - briefly, clearly and with pictures :)
- “ Notes on coding theory ”, A. Romashchenko, A. Rumyantsev, A. Shen, 2011. - a kind of "cheat sheet" - briefly, succinctly, but requires a certain level of preparation .
- You also can not ignore the seminars on "Coding Theory" , which are regularly organized by the staff of the Institute for Information Transmission Problems. A.A. Kharkevich, Russian Academy of Sciences, Moscow. Further - on the links - you can find a lot of interesting things on topics related to the mathematical theory of coding, relevant issues are raised within the discipline. For example, about sequential decoding of polar and extended Reed-Solomon codes . In the search engines you can already find articles by the author.
Source: https://habr.com/ru/post/336286/
All Articles