Kaggle Mercedes and cross-validation

Hello everyone, in this post I will talk about how I managed to take 11th place in the competition from the company Mercedes on kaggle , which can be described as a leader in the number of participants and in the epic shake-up. Here you can familiarize yourself with my decision , there is a link to github in the same place, here you can see the presentation of my solution in Yandex .

In this post we will talk about how a conservatory student got into data science, became the winner of two consecutive kaggle competitions, and how the methods of mathematical statistics help not to retrain to a public leaderboard.

I will begin by telling a little about the task and why I undertook to solve it. I must say that I am a new person in data science. About 7 years ago I graduated from the Faculty of Physics of St. Petersburg State University and since then I have been engaged in receiving a musical education. The idea of ​​stretching the brain a little and returning to technical tasks first visited me about two years ago, at that time I was already working in the Moscow Philharmonic Orchestra and was studying for the 3rd year at the Conservatory. I started with the fact that having armed myself with the Stroustrup book I began to master C ++. Further, of course, there were different online courses, and about a year ago I began to be inclined to think that Data Science was probably exactly what I would like to do in IT. My “education” in Data Science is a course from Yandex and HSE on a course , several courses from the MIPT specialization on a course and of course self-development in competitions.

I received my first kaggle medal in the competition from Sberbank - I took there 13 out of 3000+ place, here is the decision of Sberbank referring to github. And right after that, I decided to fit into the competition from Mercedes, until the end of which there were 10 days left. It was a very hard 10 days of my vacation, but, first, I discovered a lot of new things, and secondly, I got one more gold medal in the end. And in this post I would like to share what I learned, solving this problem.
')

Formulation of the problem

At the factory Mercedes there is some kind of installation that tests new cars. Testing time varies within fairly wide limits - approximately from 50 to 250 seconds. We are invited to predict this time for more than 300 different signs. All signs are anonymized, but the organizers have revealed their common meaning. There were 8 categorical signs (they took values ​​of the form A, XV, FD, B, ...), and these were the characteristics of the car. Most of the signs took the values ​​0 or 1 and were characteristics of the tests that were conducted for each specific machine.

Now that the overall plan is clear, it's time to move on to the details. Here I would like to make a reservation at once that I will not discuss further in the text the subtleties of the ensemble of algorithms or some non-trivial tricks of gradient boosting. It will be mainly about how to validate, so as not to get upset when opening a private leaderboard. If we discard all the artistic details, we have the usual regression problem on anonymized features. The peculiarity of this competition was in a small (by the standards of kaggle) dataset (train and test approximately 4000 objects) and in a very noisy target (boksplot target below).


From the boxplot it becomes obvious that we will face difficulties in validation. It can be assumed that on cross-validation we are waiting for a hefty variation of the metric over the fold. And in order to add fuel to the fire, I will clarify that the competition metric is the coefficient of determination (R2), which, as we know, is very sensitive to emissions.

The problem attracted so many participants, primarily because the baseline is written in several lines. Let's make such a baseline and look at the results of cross-validation:

import xgboost as xgb from sklearn.model_selection import cross_val_score import pandas as pd import numpy as np data = pd.read_csv('train.csv') y_train = data['y'] X_train = data.drop('y', axis=1).select_dtypes(include=[np.number]) cross_val_score(estimator=xgb.XGBRegressor(), X=X_train, y=y_train, cv=5, scoring='r2') 

The output will be something like this:

[ 0.37630003, 0.43968909, 0.5886552 , 0.54800137, 0.55752035]

The standard deviation of the folds is so large that the comparison of averages loses its meaning (in the overwhelming majority of cases, the averages will differ by less than standard deviation).

Everything that comes next consists of two parts. The first part is simple and pleasant, which caused a keen interest in training in Yandex. In it, I will tell why a large std (Standard Deviation) is not a hindrance to cross-validation and will show a beautiful and uncomplicated approach, eliminating the influence of this std. The second part is more complicated, but, in my opinion, much more important. In it, I will talk about why this is not a panacea, how cross-validation can mislead us, what it makes sense to expect from cross-validation and how to treat it. So let's go.

Comparing models on noisy data

Why do we need cross-validation? When we solve a puzzle, we try a huge number of different models and want to find the best or the best. Thus, we need a way to compare the two models and reliably select the winner from this pair. This is where we ask for help from cross-validation. I say that under the model I understand not just some kind of machine learning algorithm, but the entire pipeline, which includes data preprocessing, feature selection, creation of new features, selection of the algorithm and its hyperparameters. Any of these steps is essentially a hyperparameter of our model, and we want to find the best hyperparameters for our problem. And for this you need to be able to compare two different models. Let's try to solve this problem.

Let me remind you that the value of the loss function for the folds of cross-validation in the Mercedes task is catastrophically non-permanent. Therefore, simply comparing the average rate of the two models for cross-validation, we cannot draw any conclusions (the differences will be within the margin of error). I used this approach:

1. Make not one split into 5 folds, but 10. Now we have 50 folds, but the size of the fold remains the same. In the scores array, we get 50 skors on fifty test folds:

 import numpy as np from sklearn.model_selection import KFold, cross_val_score scores = np.array([]) for i in range(10): fold = KFold(n_splits=5, shuffle=True, random_state=i) scores_on_this_split = cross_val_score( estimator=xgb.XGBRegressor(), X=X_train, y=y_train, cv=fold, scoring='r2') scores = np.append(scores, scores_on_this_split) 

2. We will not compare the average speed of the models, but how much each model is better or worse than the other on the corresponding fold. Or, which is the same, we will compare with zero the average of the pairwise differences of the results of the two models on the respective folds .

Next, I will formalize the second paragraph a little, but now I need to understand that it’s a bang, we no longer depend on the fact that, say, in the first fold we have an outlaer, and it is always very low there. Now the fast on the first fold is not averaged with the rest, it is compared exclusively with the fast on the same fold of the second model. Accordingly, we are no longer hampered by the fact that the first fold is always worse than the second, since we compare not fast on average, but fast on each fold and then average it.

We now turn to the assessment of statistical significance. We want to answer the question: are the speeds of our two models significantly different in our 50 test folds? The short-sights of our models are linked samples, and I propose to use a statistical criterion specifically designed for such cases. This is the Student's t-test for related samples. I will not overload the post reasoning that the hypothesis of normality in our case is carried out with sufficient accuracy, and the Student’s criterion is applicable - I elaborated on this in training in Yandex, if you wish, you can watch the recording. Now I immediately go to the practical part.
Statistics t-test has the following form:

$$

$$T (X_1 ^ n, X_2 ^ n) = \ frac {E (X_1) -E (X_2)} {S / \ sqrt {n}},$$

Where $$$X_1 ^ n, X_2 ^ n$- lists of metric values ​​by test folds for the first and second models, respectively, S is the variance of pairwise differences, n is the number of folds. Here I want to make a reservation that I will not be able to describe the procedure for testing statistical hypotheses and the theory behind it. Not because it is difficult to understand, but simply because, as it seems to me, the post is not quite about that. And also because it is quite difficult to explain and, having made this post longer on two screens, I still hardly make these things clearer to people for whom they are new. In the first two weeks of this course, the topic of testing statistical hypotheses is exhaustively disclosed, I highly recommend: https://www.coursera.org/learn/stats-for-data-analysis/home/welcome .

So our null hypothesis is that both models give the same results. In this case, the t-statistic is distributed according to the Student with a mathematical expectation of 0. Accordingly, the more it deviates from 0, the less is the likelihood that the null hypothesis is fulfilled and the averages in the numerator do not coincide purely by chance. Note the denominator: S is the variance of pairwise differences . That is, we are absolutely not interested in the variance of the folds on the folds for each model separately (that is, the variance $$$X_1 ^ n$and $$$X_2 ^ n$), we are only interested in how “stable” one model is better or worse. It is for this that S is responsible, being in the denominator.

The criterion of interest to us is implemented in the scipy library in the stats module, this is the ttest_rel function. The function takes as input two lists (or arrays) of metrics on test folds, and returns the value of t-statistics and p-value for a two-sided alternative. The greater the modulus t-statistics, and the smaller the p-value, the more significant the differences. The most common practice is to assume that the differences are significant if p-value <0.05. Let's see how this works in practice:

 import xgboost as xgb from sklearn.model_selection import cross_val_score, KFold import pandas as pd import numpy as np from scipy.stats import ttest_rel data = pd.read_csv('./input/train.csv') y_train = data['y'] X_train = data.drop('y', axis=1).select_dtypes(include=[np.number]) scores_100_trees = np.array([]) scores_110_trees = np.array([]) for i in range(10): fold = KFold(n_splits=5, shuffle=True, random_state=i) scores_100_trees_on_this_split = cross_val_score( estimator=xgb.XGBRegressor( n_estimators=100), X=X_train, y=y_train, cv=fold, scoring='r2') scores_100_trees = np.append(scores_100_trees, scores_100_trees_on_this_split) scores_110_trees_on_this_split = cross_val_score( estimator=xgb.XGBRegressor( n_estimators=110), X=X_train, y=y_train, cv=fold, scoring='r2') scores_110_trees = np.append(scores_110_trees, scores_110_trees_on_this_split) ttest_rel(scores_100_trees, scores_110_trees) 

We will get the following:

Ttest_relResult(statistic=5.9592780076048273, pvalue=2.7039720009616195e-07)

The statistics is positive, it means that the numerator of the fraction is positive and, accordingly, the average $$$X_1 ^ n$more than average $$$X_2 ^ n$. Recall that we maximize the target metric R2 and realize that the first algorithm is better, that is, 110 trees on this data lose 100. P-value is significantly less than 0.05, so we boldly reject the null hypothesis, claiming that the models are significantly different. Try to calculate mean () and std () for scores_100_trees and scores_110_trees and you will see that a simple comparison of the averages does not roll here (the differences will be of the order of std). Meanwhile, the models differ, and they differ very much, and the Student's t-test for related samples helped us show it.

With this, I would finish the first part, but for some reason I already imagine how many readers, armed with this knowledge, will build a tremendous GridSearch, make thousands of arrays scores_xxx, do thousands of t-tests, comparing it all with a baseline, and choose an algorithm with the largest modulo negative t-statistics (or positive depending on the order of the arguments ttest_rel). Friends, colleagues, wait, do not do this. GridSearch is a very cunning thing. Let's remember that our t-statistics is distributed by Student. This means that, firstly, it is a random variable, and secondly, even assuming the absence of any differences, it can take values ​​from minus infinity to infinity. Consider: from minus infinity to infinity for models that in fact will give almost the same speed on new data! On the other hand, the greater the value of t-statistics in the module, the less likely it is to get it by chance. That is, for example, the probability that we get something more than 3 in absolute value is less than 0.5%. But you did GridSearch, checked several thousand different models. Obviously, even if they didn’t differ at all, at least once you’ll probably overcome this triple. And accept the wrong hypothesis.

In statistics, this is called multiple checking, and there are different methods of dealing with errors in this multiple checking. I propose to use the simplest of them - to test fewer hypotheses and to do it very intelligently. Now I will explain how I see it in practice.

Let's return to our xgboost and try to optimize the number of trees. First, I urge to optimize hyperparameters strictly one by one. Let us baseline - 100 trees. Let's see what happens with t-statistics with a gradual decrease in the number of trees to 50:

 %pylab inline t_stats = [] n_trees = [] for j in range(50, 100): current_score = np.array([]) for i in range(10): fold = KFold(n_splits=5, shuffle=True, random_state=i) scores_on_this_split = cross_val_score( estimator=xgb.XGBRegressor( n_estimators=j), X=X_train, y=y_train, cv=fold, scoring='r2') current_score = np.append(current_score, scores_on_this_split) t_stat, p_value = ttest_rel(current_score, scores_100_trees) t_stats.append(t_stat) n_trees.append(j) plt.plot(n_trees, t_stats) plt.xlabel('n_estimators') plt.ylabel('t-statistic') 

What we see on the chart is a good situation. When we have about 50 trees, the model answers are not much different from a baseline with a hundred trees. As the number of trees increases, the differences increase, the algorithm begins to predict better: somewhere around 85 we have an optimum, and then the t-statistics drops, that is, the algorithm approaches our baseline. Looking at the graph it becomes obvious that the optimal number of trees is about 83. And it is quite possible to take 81, 82, 83, 84, 85 and average. This kind of averaging allows us, practically free of charge in the sense of our efforts, to improve the generalizing ability and the final speed, I often use this technique. I hope that from all these considerations it becomes clear that on such graphs we are interested in not just the global optimum, but the optimum, to which the function smoothly tends and from which it smoothly leaves. With a sufficiently large number of points on the graph, we may well get random bursts, which may be more of the optimum of interest. But we differ from GridSearch, including the fact that we will take not just a point with a maximum (minimum) value of t-statistics, but we will approach this a bit more intelligently.

It is in order to be able to look at these graphs, I urge to optimize the hyperparameters in turn. In some cases, it can be justified to switch to a 3-dimensional scatter-plot, where you can monitor the metric depending on two hyperparameters.

Unfortunately, I can’t summarize the first part of the view plan first, do it this way, then this way, since setting up hyper-parameters for cross-validation is a very delicate matter and requires constant analysis. The only thing on which I unequivocally insist: never try to get into the top ten - this is impossible. The fact that the cross-validation of 148 trees is better than 149 does not at all mean that the test will be the same. Not sure - average, because averaging is one of the very few things that the model: a) definitely does not spoil, b) is likely to improve. And be careful with GridSearch - this algorithm is very good at creating the appearance of optimization of hyper parameters. At least for the hyperparameters that you consider important in this task, you need to manually make sure that you find a really optimal value, and not a random surge in white noise.

Danger of retraining on emissions

In the second part of my post, I will talk about what cross-validation is in principle, in what and how it can help us, and in what it cannot. The background is as follows: applying the validation, which I mentioned in the first part, I began to improve the model: something to twist somewhere, select features, add new ones, in general do what we always do when deciding kaggle. I approached the testing of statistical hypotheses very conservatively, tried to check them as little as possible and as reasonably as possible. Pretty quickly, I came to the conclusion that the average R2 for cross-validation was about 0.58. As we know today, the best private leaderboard is 0.5556. But then I did not know this, and in public (public leader) the top was already 0.63+, although it was clear that it was absolutely useless to look at other people's public (leader probing in this competition had an unprecedented scale). The cold shower happened when I made the best one, in my opinion, the model and got on public 0.54, despite the fact that the baseline gave 0.55. It became obvious that something was wrong here.

At this point I would like to dwell a little more. If, for example, it was not a kaggle, but a job, I would have every chance to send such a model to production (at least try to do it). It would seem that this? I have such a clever cross-validation, I very carefully picked up all the parameters and got a high speed, what could be the questions? But you need to understand and always remember what I then forgot about - in principle, cross-validation cannot evaluate the performance of a model on new data. Just in case, I will explain that the word performance (eng. Performance) I denote the quality of the model in terms of the selected metric. You cross-validate again and again, choosing only those models that work best on test folds. Not on some test folds, but on very specific and identical test folds. And even if you, say, periodically change the random_state from Kfold, thus making the folds different, they still, ultimately, are assembled from the objects of your training set. And, selecting hyper parameters, you train the algorithm on these objects. If the data is good, and we did everything carefully, then this may lead to the fact that the algorithm will work a little better on new objects, but in the general case it’s not worth waiting for the same performance. And in the case when the data is quite noisy, there is a risk of encountering a situation that I encountered and which I will discuss until the end of the post.

For myself, I realized that it is absolutely necessary to have a delayed selection in any task. I would suggest doing so: we received the task — we immediately made a delayed selection and threw it out of the train. Calculated what result baseline on this sample. Then it is possible to improve the model for a long time and persistently, and finally, when the best model is already ready, it is time to look quickly at the delayed sample. In the case of kaggle, a public leaderboard can play the role of a delayed selection. But it is important to remember that the more often we look at the fast delayed sample, the worse it estimates the performance of the model on the new data.

Back to the Mercedes. Having received in public faster faster than my baseline, I realized that I had retrained. Now I will demonstrate how retraining takes place with a seemingly correct approach to the selection of hyper parameters. For clarity, we will have only one feature. Let the true relationship be a sine, add normal noise and add normal emissions (15% less objects for objects, 4% less for emissions):

 import numpy as np import seaborn as sns import numpy as np %pylab inline np.random.seed(3) X = 8 * 3.1415 * np.random.random_sample(size=2000) y = np.sin(X) + np.random.normal(size=X.size, scale=0.3) outliers_1 = np.random.randint(low=0, high=X.shape[0], size=int(X.shape[0] * 0.15)) y[outliers_1] += np.random.normal(size=outliers_1.size, scale=1) outliers_2 = np.random.randint(low=0, high=X.shape[0], size=int(X.shape[0] * 0.04)) y[outliers_2] += np.random.normal(size=outliers_2.size, scale=3) sns.boxplot(y) plt.show() plt.scatter(x=X, y=y) plt.show() 

Boxsplot is somewhat similar to what we saw for a target in a task from Mercedes, but outliers are present on both sides.



Let the first thousand objects be our training sample, the second one is a test one. Calculate the baseline speed on cross-validation:

 import xgboost as xgb from sklearn.model_selection import cross_val_score,KFold from scipy.stats import ttest_rel X_train = X[:X.shape[0]/2].reshape(-1,1) y_train = y[:X.shape[0]/2] X_test = X[X.shape[0]/2:].reshape(-1,1) y_test = y[X.shape[0]/2:] base_scores_train = np.array([]) for i in range(10): fold = KFold(n_splits=5, shuffle=True, random_state=i) scores_on_this_split = cross_val_score( estimator=xgb.XGBRegressor( min_child_weight=2), X=X_train, y=y_train, cv=fold, scoring='r2') base_scores_train = np.append(base_scores_train, scores_on_this_split) 

Now, just like we did in the first part, let's compare the model with a baseline with fewer trees and look at the dependence of t-statistics on n_estimators:

 t_stats_train = [] for j in range(30, 100): scores_train = np.array([]) for i in range(10): fold = KFold(n_splits=5, shuffle=True, random_state=i) scores_on_this_split = cross_val_score( estimator=xgb.XGBRegressor( n_estimators=j, min_child_weight=2), X=X_train, y=y_train, cv=fold, scoring='r2') scores_train = np.append(scores_train, scores_on_this_split) t_stat,p_value = ttest_rel(scores_train, base_scores_train) t_stats_train.append(t_stat) plt.plot(range(30, 100), t_stats_train) plt.xlabel('n_estimators') plt.ylabel('t-statistic') 

We obtain a very beautiful graph, from which we conclude that it is optimal to take approximately 85 trees:



But let's see how these algorithms will behave on new data:

 est_base = xgb.XGBRegressor(min_child_weight=2) est_base.fit(X_train, y_train) base_scores_test = r2_score(y_test, est_base.predict(X_test)) scores_test = [] for i in range(30,101): est = xgb.XGBRegressor(n_estimators=i, min_child_weight=2) est.fit(X_train,y_train) scores_test.append(r2_score(y_test, est.predict(X_test))) plt.plot(range(30, 101), scores_test) plt.xlabel('n_estimators') plt.ylabel('r2_score_test') 

We are surprised to find that 85 is far from the optimal number of trees for our dataset. Of course, emissions are to blame for this, and it seems to me that I got into a Mercedes competition at this particular situation. If you experiment with this code, you will see that it is not necessarily the optimum on the train will be to the right of the optimum on the test, but quite often their x-coordinate will not match.

In order to assess how strongly emissions are affected by the speed, I propose to torture this line:

 from sklearn.metrics import r2_score r2_score( [1, 2, 3, 4, 5, 11], [1.1, 1.96, 3.1, 4.5, 4.8, 5.3] ) 

Please note that if we, for example, write 1.0 in the second array, will soon change in the fourth digit. And now let's try to get 0.1 closer to our Outlaer - replace 5.3 by 5.4. The speed changes immediately to 0.015, that is, about 100 times stronger than if we would have improved the prediction of the “normal” value by the same amount.Thus, the speed is mainly determined not by how accurately we predict the “normal” values, but by which of the models turned out to be a little better on emissions. And it becomes clear that by selecting features and setting up hyper parameters, we involuntarily select those models that guess the outliers on test folds a little better, and not those that better predict the main mass of objects. This happens simply because models that guess outlayers get higher fast, and performance on the main mass of objects does not have a strong effect on fast.

In most tasks, I suppose, emissions are unpredictable. This needs to be verified, and if so, admit it openly. And since we cannot predict them, let us not take them into account when comparing models. Indeed, if any of our models will equally badly predict emissions from new data, then what’s the point in estimating emissions predictions for cross-validation? There are two strategies of behavior in such situations:

1. Let's remove all outliers from the training set and only after that we will train and validate the models. On how to remove emissions, let's talk a little later, while we believe that somehow we are able to do it. Such a strategy is really very strong, the winner of the Sberbank Russian Housing Market competition was Yevgeny Patekh validated like this: youtu.be/Eo4WMlcT7uo, www.kaggle.com/c/sberbank-russian-housing-market/discussion/35684 . The only problem with this method is that often throwing out outlayers shifts the average prediction, and we have to somehow compensate for this shift.

2. We will not remove anything from the training set, but during validation (when calculating the value of a metric on test folds) we will not take into account outliers. I used just such a scheme. You can find my implementation of such cross-validation in this repository., a function called cross_validation_score_statement, is defined in the cross_val_custom.py file. Once again, we do everything up to calling the fit method (and including it) without throwing out anything, then we do the predict on test folds, but we consider the metric only on objects that are not outliers.

As I have already said, having received a very low fast in public, I realized that I had retrained. When I started validating without outlayers, this retraining immediately became apparent. It turned out that I too aggressively selected signs that I had grown too many trees for my xgboost'ov. It turned out to be very easy to fix, I spent about an hour trying to find a new optimum in the space of hyperparameters, and the result was overloaded. The transition to validation without outlayers made a decision on the 11th place from the 3000+ decision on Privat.

Let's show how this works on our toy dataset. First, it is necessary to decide who should be considered an outlaire. I considered the autlae objects, on which the baseline is wrong most of all (the error out-of-fold prediction is more than a certain threshold). The threshold is selected on the basis of how many percent of the training sample you want to declare as an autlaier.

 from sklearn.model_selection import cross_val_predict base_estimator = xgb.XGBRegressor(min_child_weight=2) pred_train = cross_val_predict(estimator=base_estimator, X=X_train, y=y_train, cv=5) abs_train_error = np.absolute(y_train - pred_train) outlier_mask = (abs_train_error > 1.5) print 'Outliers fraction in train = ',\ float(y_train[outlier_mask].shape[0]) / y_train.shape[0] 

We'll get:

Outliers fraction in train = 0.045

That is, 4.5% of objects are declared emissions. Now we calculate the speed on cross-validation for baseline, and then we will change the number of trees. Only now the emissions will not be taken into account when calculating the skora.

 # import cross_val_custom from # https://github.com/Danila89/cross_validation_custom from cross_val_custom import cross_validation_score_statement from sklearn.metrics import r2_score base_scores_train_v2 = np.array([]) for i in range(10): scores_on_this_split = cross_validation_score_statement( estimator=xgb.XGBRegressor( min_child_weight=2), X=pd.DataFrame(X_train), y=pd.Series(y_train), scoring=r2_score, n_splits=5, random_state=i, statement=~outlier_mask) base_scores_train_v2 = np.append(base_scores_train_v2, scores_on_this_split) t_stats_train_v2 = [] for j in range(30, 100): scores_train_v2 = np.array([]) for i in range(10): fold = KFold(n_splits=5, shuffle=True, random_state=i) scores_on_this_split = cross_validation_score_statement( estimator=xgb.XGBRegressor( n_estimators=j, min_child_weight=2), X=pd.DataFrame(X_train), y=pd.Series(y_train), scoring=r2_score, n_splits=5, random_state=i, statement=~outlier_mask) scores_train_v2 = np.append(scores_train_v2, scores_on_this_split) t_stat,p_value = ttest_rel(scores_train_v2, base_scores_train_v2) t_stats_train_v2.append(t_stat) plt.plot(range(30,100), t_stats_train_v2) plt.xlabel('n_estimators') plt.ylabel('t-statistic') 

We get this schedule:



It is evident that, unfortunately, this is not a silver bullet, and the optimum is still not on 50 trees, as we would like. But this is not 85 as it was before, and the extremum is not so obvious, which suggests that it makes sense to average by the number of trees from 60 to 95. And having done this, we will quite possibly get a result comparable to that we would get if we knew that we actually need to take 50.

And the last thing I want to show is how the predictions of our boost actually change as the number of trees grows, the benefit in the one-dimensional case can be done. For different n_estimators, I will build predictions of the algorithm and glue it into gif:

 X_plot = np.linspace(0,8 * 3.1415, num=2000) est = xgb.XGBRegressor(n_estimators=70, min_child_weight=2) est.fit(X_train, y_train) plt.plot(X_plot, est.predict(X_plot.reshape(-1, 1))) plt.xlabel('X') plt.ylabel('Prediction')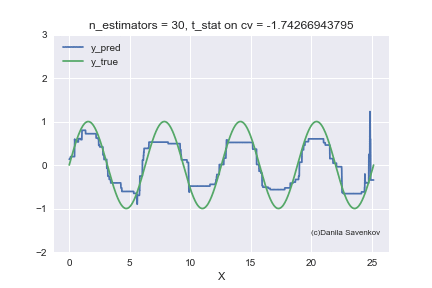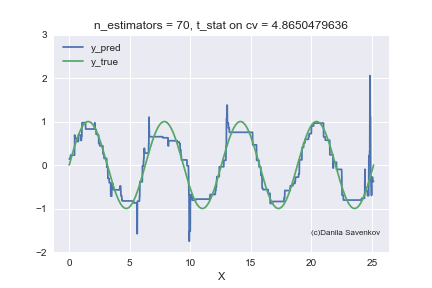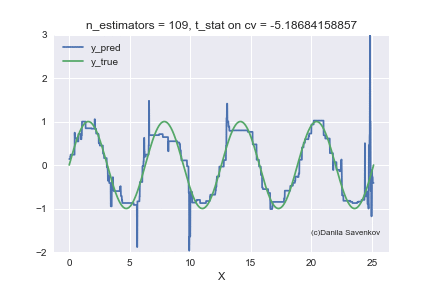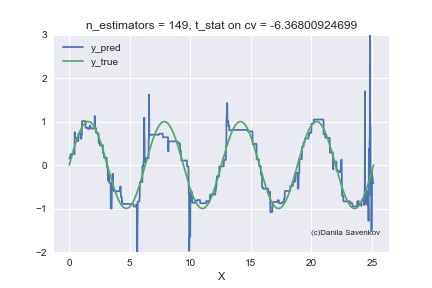 

We see how strong outlayers interfere with our model. We also see that after approximately n_estimators = 60, the model actually stops approaching from the original function and only deals with the fact that it retrains on emissions from the training set. Recall that 50 trees show themselves best on our “new” data. And in the animation with n_estimators = 60, 70, 80, the t-statistics on cross-validation continues to increase, and it increases thanks to the successful hit in the outlayers. When I made this animation, the idea of ​​teaching models on a clean dataset seemed to me even more attractive. You can say a lot more by looking at this gif, but I don’t dare detain you anymore.

I really hope that you do not regret the evening spent on reading this post.of time. This topic is complex, ambiguous and interesting, I will be happy for your comments and the opportunity to continue the discussion, but not in monologue mode.