Memoization and Currying (Python)
Hello, dear readers Habrahabra. In this article we will try to understand what memoization and currying are, and how these methods are implemented in the standard Python library.
This is an optimization method in which the result of the function execution is saved and this result is used during the next call.
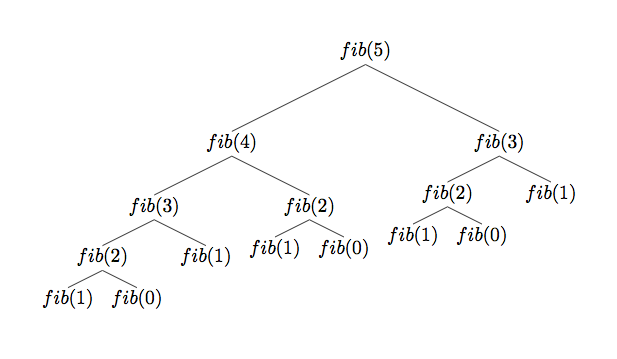
We take the recursive implementation of finding the Fibonacci number and look at the execution time.
')
The operation time will grow very quickly with an increase in the number to be found, plus a RecursionError error is possible.
To optimize such an algorithm, the method of memoization is well suited, that is, saving and reusing early computed values (but from the beginning, of course, you should try to completely abandon the recursive algorithm).
Or in the form of a decorator:
And the good news is that in the standard functools library, the similar decorator lru_cache is already perfectly implemented.
LRU stands for Least Recently Used.
lru_cache has two optional arguments.
maxsize is the number of stored results.
typed - if true, for example, values 1 and 1.0 will be considered different.
Memoization is a fairly simple and effective practice. Thanks to functools.lru_cache, it’s convenient to use in Python. Under the hood she has a dictionary in the form of a hash table, respectively, the key must implement hashing.
Currying is the transformation of a function from many arguments into a set of functions, each of which is a function of one argument. We can pass part of the arguments to the function and get back the function that waits for the remaining arguments.
Create a simple greet function that accepts a greeting and a name as arguments:
A small improvement will allow us to create a new function for any type of greeting and transfer the name to this new function:
And then you can do it with any number of arguments:
Or option with lambda:
This is the process of applying a function to a portion of its arguments.
In other words, a function that accepts a function with several parameters and returns a function with fewer parameters.
Partial application converts the function from n arguments to (xn), and curring creates n functions with 1 arguments.
Python has this feature in the standard library library; this is a function
partial.
Another example with partial solves the closure problem in a cycle:
That's all for today. Thank!
Memoization
This is an optimization method in which the result of the function execution is saved and this result is used during the next call.
We take the recursive implementation of finding the Fibonacci number and look at the execution time.
@clock def fib(n): if n < 2: return n return fib(n-2) + fib(n-1) print('fib(20) =', fib(20)) [0.35938287s] fib(20) -> 6765 @clock
def clock(func): def clocked(*args, **kwargs): t0 = time.time() result = func(*args, **kwargs) # elapsed = time.time() - t0 name = func.__name__ arg_1st = [] if args: arg_1st.append(', '.join(repr(arg) for arg in args)) if kwargs: pairs = ['%s=%r' % (k, w) for k, w in sorted(kwargs.items())] arg_1st.append(', '.join(pairs)) arg_str = ', '.join(arg_1st) print('[%0.8fs] %s(%s) -> %r' % (elapsed, name, arg_str, result)) return result return clocked 
')
The operation time will grow very quickly with an increase in the number to be found, plus a RecursionError error is possible.
To optimize such an algorithm, the method of memoization is well suited, that is, saving and reusing early computed values (but from the beginning, of course, you should try to completely abandon the recursive algorithm).
_fib_cache = {1: 1, 2: 1} # - , - @clock def mem_fib(n): result = _fib_cache.get(n) if result is None: result = mem_fib(n-2) + mem_fib(n-1) _fib_cache[n] = result return result print('mem_fib(200) =', mem_fib(200)) [0.03125453s] mem_fib(200) -> 280571172992510140037611932413038677189525 Or in the form of a decorator:
def memoize(f): cache = {} def decorate(*args): if args in cache: return cache[args] else: cache[args] = f(*args) return cache[args] return decorate # lambda # def memoize(f): # cache = {} # return lambda *args: cache[args] if args in cache else cache.update({args: f(*args)}) or cache[args] # # def memoize(f): # cache = {} # # def decorate(*args, **kwargs): # key = (tuple(args), hash(tuple(sorted(kwargs.items())))) # if key not in cache: # cache[key] = f(*args, **kwargs) # return cache[key] # # return decorate @clock @memoize def fib(n): if n < 2: return n return fib(n-2) + fib(n-1) print('fib(20) =', fib(20)) And the good news is that in the standard functools library, the similar decorator lru_cache is already perfectly implemented.
LRU stands for Least Recently Used.
from functools import lru_cache @clock @lru_cache() def fib(n): if n < 2: return n return fib(n-2) + fib(n-1) print('fib(20) =', fib(20)) lru_cache has two optional arguments.
maxsize is the number of stored results.
typed - if true, for example, values 1 and 1.0 will be considered different.
Memoization is a fairly simple and effective practice. Thanks to functools.lru_cache, it’s convenient to use in Python. Under the hood she has a dictionary in the form of a hash table, respectively, the key must implement hashing.
Now about currying or currying
Currying is the transformation of a function from many arguments into a set of functions, each of which is a function of one argument. We can pass part of the arguments to the function and get back the function that waits for the remaining arguments.
Create a simple greet function that accepts a greeting and a name as arguments:
def greet(greeting, name): print(greeting + ', ' + name) greet('Hello', 'German') A small improvement will allow us to create a new function for any type of greeting and transfer the name to this new function:
def greet_curried(greeting): def greet(name): print(greeting + ', ' + name) return greet greet_hello = greet_curried('Hello') greet_hello('German') greet_hello('Ivan') # greet_curried greet_curried('Hi')('Roma') And then you can do it with any number of arguments:
def greet_deeply_curried(greeting): def w_separator(separator): def w_emphasis(emphasis): def w_name(name): print(greeting + separator + name + emphasis) return w_name return w_emphasis return w_separator greet = greet_deeply_curried("Hello")("...")(".") greet('German') greet('Ivan') Or option with lambda:
greet_deeply_curried = lambda greeting: lambda separator: lambda emphasis: lambda name: \ print(greeting + separator + name + emphasis) Partial application
This is the process of applying a function to a portion of its arguments.
In other words, a function that accepts a function with several parameters and returns a function with fewer parameters.
Partial application converts the function from n arguments to (xn), and curring creates n functions with 1 arguments.
Python has this feature in the standard library library; this is a function
partial.
from functools import partial def greet(greeting, separator, emphasis, name): print(greeting + separator + name + emphasis) newfunc = partial(greet, greeting='Hello', separator=',', emphasis='.') newfunc(name='German') newfunc(name='Ivan') newfunc2 = partial(greet, greeting='Hello', emphasis='.') newfunc2(name='German', separator='...') newfunc2(name='Ivan', separator='..') Another example with partial solves the closure problem in a cycle:
from functools import partial def makeActions(): acts = [] for i in range(5): def func(x, y): return x * y acts.append(partial(func, y=i)) # acts.append(partial(lambda x, y: x * y, y=i)) # lambda # return [partial(lambda x, y: x * y, y=i) for i in range(5)] # return acts for act in makeActions(): print(act(1), end=', ') That's all for today. Thank!
Source: https://habr.com/ru/post/335866/
All Articles