Random RPG damage distribution

In order to calculate the damage from an attack , tabletop role-playing games like Dungeons & Dragons use damage rolls . This is logical for a game whose process is based on dice rolls. In many computer RPGs, damage and other attributes (strength, magic points, dexterity, etc.) are calculated using a similar system.

Usually, the random() call code is written first, and then the results are adjusted and adjusted to the desired behavior of the game. This article will cover three topics:
')

1. Simple adjustments - mean and variance
2. Add asymmetry - discarding results or adding critical hits
3. Full freedom in setting up random numbers, unlimited opportunities for cubes

The basics

This article assumes that you have a random( N ) function that returns a random integer between 0 and range-1 . In Python, you can use random.randrange( N ) . In Javascript you can use Math.floor( N * Math.random()) . The standard C library has rand() % N , but it doesn’t work well, so use another random number generator. In C ++, you can connect uniform_int_distribution(0, N -1) to a random number generator object . In Java, you can create a random number generator object with new Random() , and then call .nextInt( N ) for it. Standard libraries in many languages ​​do not have good random number generators, but there are many third-party libraries, for example, PCG for C and C ++.

Let's start with one die. This histogram shows the results of one 12-sided dice rolls: 1+random(12) . Since random(12) returns a number from 0 to 11, and we need a number from 1 to 12, we add 1 to it. On the X axis, the damage is located, on the Y axis - the frequency of receiving the corresponding damage. For one dice, a roll of damage 2 or 12 is just as likely as a roll 7.



To throw a few dice, it is useful to use the record used in games with dice: N d S means that you need to throw an S- side bone N times. A roll of one 12-sided dice is recorded as sided 1d12; 3d4 means throwing 4-sided dice three times. In the code, this can be written as 3 + random(4) + random(4) + random(4) .

Let's throw two 6-sided dice (2d6) and summarize the results:

 damage = 0 for each 0 ≤ i < 2: damage += 1+random(6) 

Results can be in the range from 2 (on both bones, 1) to 12 (on both bones, 6). The probability of getting 7 is higher than 12.



What happens if we increase the number of bones, but reduce their size?







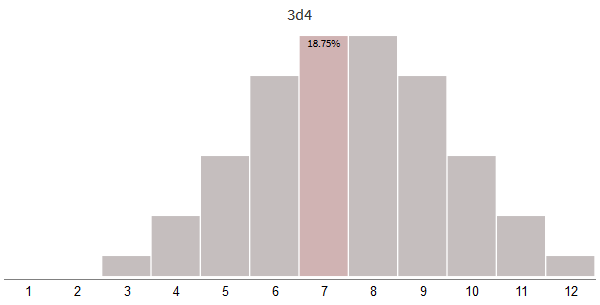
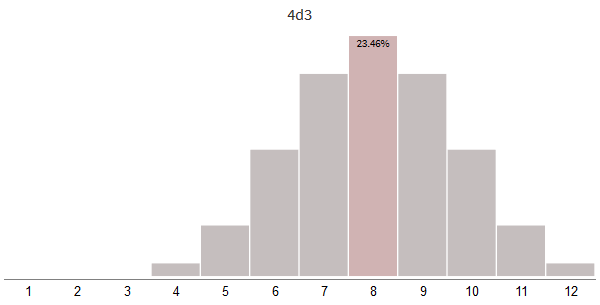
The most important effect - the distribution will not be wide , but narrow . There is a second effect - the peak is shifted to the right. Let's first explore the use of offsets.

Permanent offsets

Some of the weapons in Dungeons & Dragons give bonus damage. You can write 2d6 + 1 to indicate the bonus +1 to damage. In some games, armor or shields reduce damage. You can write 2d6-3, which means removing 3 points of damage (in this example, I assume that the minimum damage is 0).

Let's try to shift the damage to the negative (to reduce the damage) or to the positive (for the damage bonus) side:









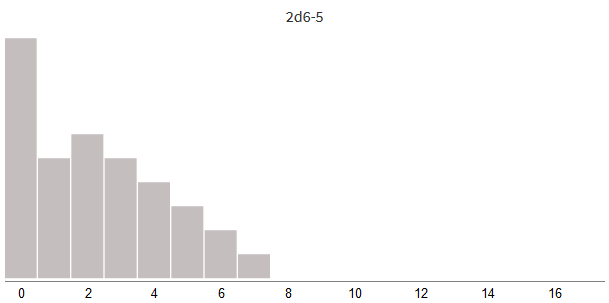
Adding damage bonus or subtracting the blocked damage, we simply shift the entire distribution to the left or to the right.

Distribution variance

When moving from 2d6 to 6d2, the distribution becomes narrower and shifts to the right. As we saw in the previous section, offset is a simple shift. Let's look at the variance of the distribution.

Define a function for N consecutive random( S+1 ) throws random( S+1 ) , returning a number from 0 to N * S :

 function rollDice(N, S): #  N ,       0  S value = 0 for 0 ≤ i < N: value += random(S+1) return value 

Generating random numbers from 0 to 24 using several bones gives the following distribution of results:









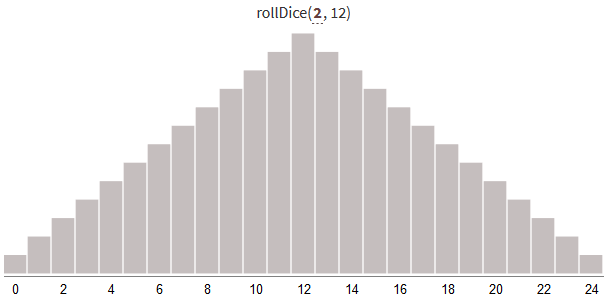
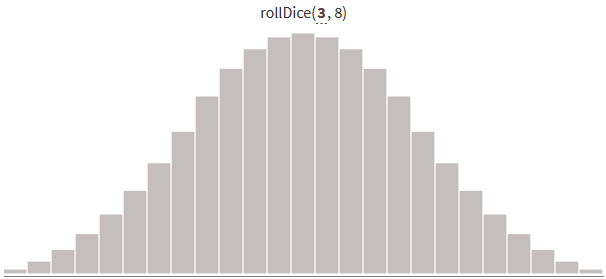
With an increase in the number of shots and maintaining a constant range from 0 to N * S, the distribution becomes narrower (with less variance). More results will be near the middle of the range.

Note: with an increase in the number of sides S (see pictures below) and dividing the result by S, the distribution approaches the normal one . A simple way to randomly select from a normal distribution is the Box-Muller transform .

Asymmetry

Distributions for rollDice( N , S ) symmetric . Values ​​below the average are as likely as values ​​above the average. Is this suitable for your game? If not, there are different asymmetry techniques.

Cutting throws or throwing

Suppose we want the values ​​above the average to be more frequent than the below average. Such a scheme is rarely used for damage, but is applicable for attributes such as strength, intelligence, etc. One of the ways to implement it is to make several throws and choose the best result.

Let's try to roll rollDice(2,20) cubes and select the maximum result:

 roll1 = rollDice(2, 20) roll2 = rollDice(2, 20) damage = max(roll1, roll2)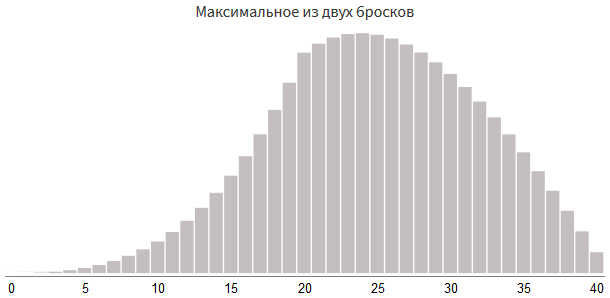 

When choosing the maximum of rollDice(2, 12) and rollDice(2, 12) , we will get a number from 0 to 24. Another way to get a number from 0 to 24 is to use rollDice(1, 12) three times and select the best two of three results. The form will be even more asymmetric than when choosing one of two rollDice(2, 12) :

 roll1 = rollDice(1, 12) roll2 = rollDice(1, 12) roll3 = rollDice(1, 12) damage = roll1 + roll2 + roll3 #   : damage = damage - min(roll1, roll2, roll3)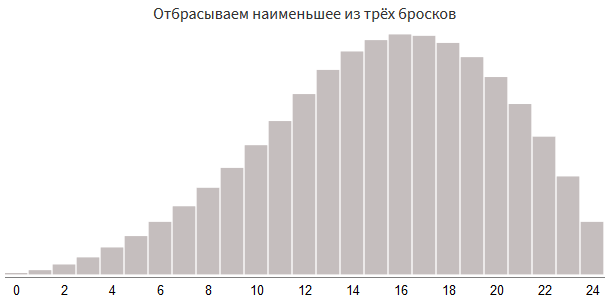 

Another way is to transfer the lowest result. In general, it is similar to the previous approaches, but slightly different in implementation:

 roll1 = rollDice(1, 8) roll2 = rollDice(1, 8) roll3 = rollDice(1, 8) damage = roll1 + roll2 + roll3 #      : damage = damage - min(roll1, roll2, roll3) + rollDice(1, 8) 

Any of these approaches can be used for inverse asymmetry, making the values ​​more frequent less than the average. We can also assume that the distribution creates random bursts of high values. This distribution is often used for damage and rarely for attributes. Here max() we change to min() :

 roll1 = rollDice(2, 12) roll2 = rollDice(2, 12) damage = min(roll1, roll2)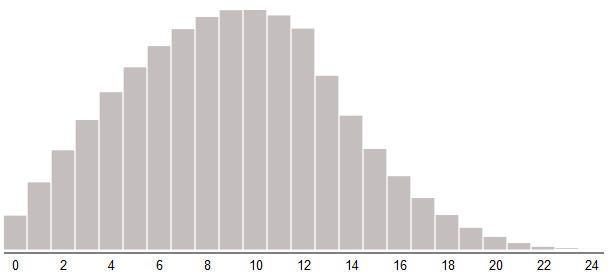 

Drop the largest of two shots.

Critical hits

Another way to create random high damage bursts is to implement them more directly. In some games, a certain bonus gives a "critical hit". The simplest bonus is extra damage. In the code below, the damage from critical hit is added in 5% of cases:

 damage = rollDice(3, 4) if random(100) < 5: damage += rollDice(3, 4)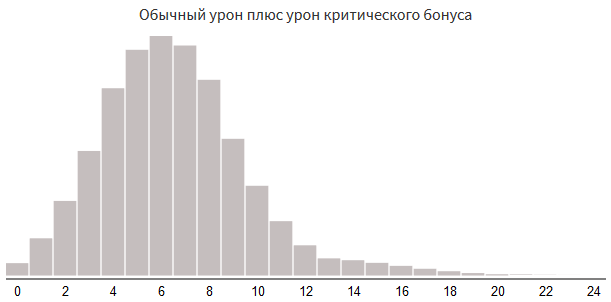 

Critical damage rate 5%


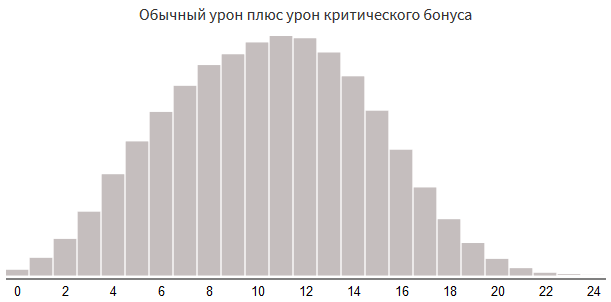
Critical damage rate 60%.

In other approaches to adding asymmetry, additional attacks are used: during critical strikes, there is a chance that additional critical blows will trigger; during critical strikes, the second attack is triggered, breaking through the defense; during critical strikes, the enemy misses the attack. But in this article I will not consider the distribution of damage in multiple attacks.

Let's try to create our own distribution.

When using randomness (damage, attributes, etc.), we must begin with a description of the distribution characteristics that we need for the game process:

• Interval: what are the minimum and maximum values ​​(if any)? Use scaling and offset to fit the distribution in this interval.
• Dispersion: how often should the values ​​be close to the mean? You can use fewer shots for more variance or more for less variance.
• Asymmetry: Do I need to more often meet the values ​​of more or less than the average? Use min, max or critical bonuses to add asymmetry to the distribution.

Here are a couple of examples with some of the parameters:

 value = 0 + rollDice(3, 8) # Min  : value = min(value, 0 + rollDice(3, 8)) # Max  : value = max(value, 0 + rollDice(3, 8)) #  : if random(100) < 15: value += 0 + rollDice(7, 4) 

 value = 0 + rollDice(3, 8) # Min  : value = min(value, 0 + rollDice(3, 8))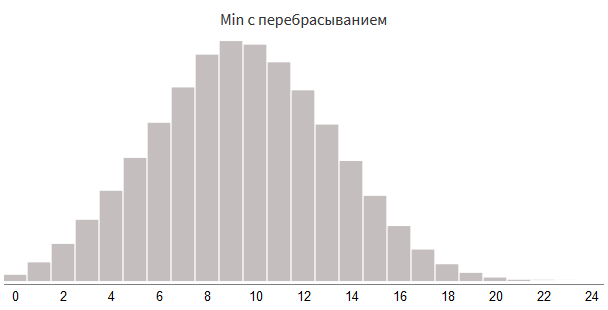 

 value = 0 + rollDice(3, 8) # Max  : value = max(value, 0 + rollDice(3, 8)) #  : if random(100) < 15: value += 0 + rollDice(7, 4)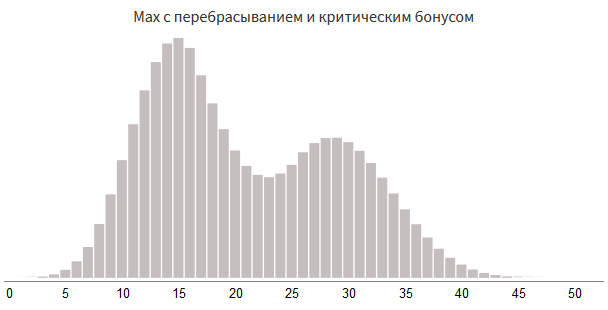 

There are many other ways of structuring random numbers, but I hope these examples gave an idea of ​​how flexible the system is already. It’s also worth looking at this damage roll calculator . However, sometimes a combination of dice rolls is not enough.

Arbitrary forms

We started with input algorithms and studying the corresponding output distributions. We had to go through a lot of input algorithms to find the result we needed. Is there a more direct way to get the right algorithm? Yes!

Let's do the opposite and start with the output we need, presented in the form of a histogram. Let's try to do it with a simple example.

Suppose I need to choose from 3, 4, 5, and 6 in the following proportions:



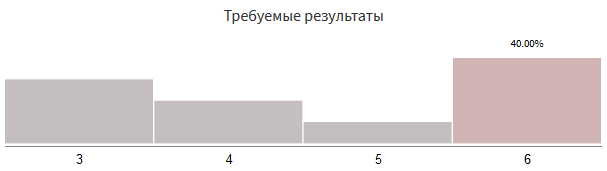
It does not correspond to anything that can be obtained by throwing bones.

How to write code for these results?

 x = random(30+20+10+40) if x < 30: value = 3 else if x < 30+20: value = 4 else if x < 30+20+10: value = 5 else: value = 6 

Examine this code and figure out how it works before proceeding to the next steps. Let's make the code more general so that it can be used for different probability tables. The first step is to create the table:

 damage_table = [ #  (, ) (30, 3), (20, 4), (10, 5), (40, 6), ]; 

In this hand-written code, each if construct compares x with the total amount of probabilities. Instead of writing separate if constructions with manually set amounts, we can cycle through all the records in the table:

 cumulative_weight = 0 for (weight, result) in table: cumulative_weight += weight if x < cumulative_weight: value = result break 

The last thing to summarize is the sum of the table entries. Let's calculate the sum and use it to select a random x:

 sum_of_weights = 0 for (weight, value) in table: sum_of_weights += weight x = random(sum_of_weights) 

Combining everything together, we can write a function to search for results in the table and a function to select a random result (you can turn them into methods of the damage table class):

 function lookup_value(table, x): # ,  0 ≤ x < sum_of_weights cumulative_weight = 0 for (weight, value) in table: cumulative_weight += weight if x < cumulative_weight: return value function roll(table): sum_of_weights = 0 for (weight, value) in table: sum_of_weights += weight x = random(sum_of_weights) return lookup_value(damage_table, x) 

The code for generating numbers from a table is very simple. It was fast enough for my tasks, but if the profiler reports that it is too slow, try speeding up the linear search with a binary / interpolation search, lookup tables, or a pseudonymity method . See also inverse transform method .

Draw your own distribution

This method is convenient because it allows you to use any form.

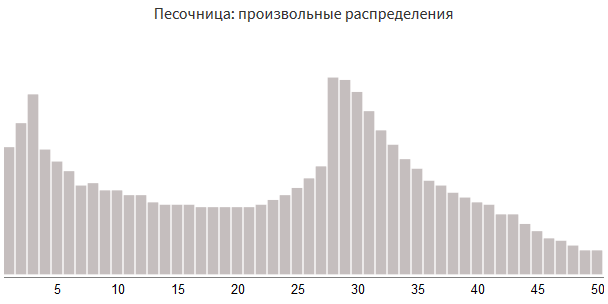
 damage_table = [(53,1), (63,2), (75,3), (52,4), (47,5), (43,6), (37,7), (38,8), (35,9), (35,10), (33,11), (33,12), (30,13), (29,14), (29,15), (29,16), (28,17), (28,18), (28,19), (28,20), (28,21), (29,22), (31,23), (33,24), (36,25), (40,26), (45,27), (82,28), (81,29), (76,30), (68,31), (60,32), (54,33), (48,34), (44,35), (39,36), (37,37), (34,38), (32,39), (30,40), (29,41), (25,42), (25,43), (21,44), (18,45), (15,46), (14,47), (12,48), (10,49), (10,50)] 

With this approach, we can choose a distribution that matches any game process that is not limited to the distributions created by the roll of the dice.

Conclusion

Random damage rolls and random attributes are implemented simply. You, as a game designer, must choose the properties that the final distribution will have. If you use dice rolls:

• To control the variance, use the number of shots. A small amount corresponds to a high dispersion, and vice versa.
• To control the scale, use the offset and bone size . If you want random numbers to be in the range from X to Y , then for each of the N shots a random number from 0 to (YX) / N should be obtained, after which X is added to it. Positive shifts can be used for damage bonuses or attribute bonuses. Negative offsets can be used to block damage.
• For more frequent values ​​greater or less than the average, use asymmetry . For attribute throws, values ​​more often than the average are required, they can be obtained by choosing the maximum, the best of the three, or moving the minimum value. For damage rolls, values ​​that are often lower than the average are required, they can be obtained by choosing the minimum or critical bonuses. For the complexity of random encounters with enemies, values ​​below average are also often used.

Think about how the distribution should vary in your game. Attack bonuses, damage blocking, and critical hits can be used to vary the distribution with simple parameters. These parameters can be associated with objects in the game. Use the sandbox in the original article to see how these parameters affect the distribution. Think about how the distribution should work when you increase the level of the player; See on this page for information on increasing and decreasing variance over time when calculating distributions using AnyDice (about which there is an excellent blog ).

Unlike board game players with dice, you are not limited to distributions based on sums of random numbers. Using the code written in the section “Let's try to create your own distribution”, you can use any distribution . You can write a visual tool that allows you to draw histograms, save data to tables, and then draw random numbers based on this distribution. You can change the table in JSON or XML. You can also edit tables in Excel and export them to CSV. Distributions without parameters provide more flexibility, and using data tables instead of code allows you to perform quick iterations without recompiling the code.

There are many ways to implement interesting probability distributions based on simple code. First, determine the properties that you need, and then select the code for them.