Random forest vs neural network: who will better cope with the task of recognizing gender in speech (part 2)
The first part of our guide was devoted to an interesting machine learning task - recognizing gender by voice. We described the general approach to most of the problems of speech processing and with the help of a random forest trained on the statistics of acoustic attributes, we solved the problem with a rather high accuracy - 98.4% of correctly classified audio fragments.
In the second part of the guide, we will see if neural networks can cope with this task more effectively than a random forest, and also try to take into account the biggest drawback of classical methods - the inability to work with data sequences.
In a sense, this stage is redundant: the sex of a person does not change during a conversation (at least at the current stage of development and under the specified standard conditions), therefore, it is not worth counting on an increase in accuracy. But for academic purposes, we will try.
')
 / Photograph by Tristan Bowersox / CC-SA
/ Photograph by Tristan Bowersox / CC-SA
It is believed that the artificial neural network (neural network) is a mathematical model of the human brain. Actually, no : 50-60 years ago, biologists at a certain level studied the electrical processes in the brain, and mathematicians created a simplified model and programmed it.
It turned out that such structures are able to solve some simple problems, but a) worse than classical methods and b) much slower than them. And the undisputed status quo persisted for half a century - scientists developed a theory (teaching methods, architectures, fundamental mathematical questions), and computer hardware and software developed so that it became possible to solve some problems on a home PC at the world level.
But not everything is so smooth: a neuronet can learn to distinguish a cheetah from a leopard, and can consider one of these animals a spotted sofa. In addition, the processes of teaching a person and a machine are different: a computer needs thousands of teaching examples, while a person needs several. Obviously, the work of artificial neural networks is not very similar to human thinking, and they are not a computer model of the brain, but just another class of models in the list: Random Forest, SVM, XGBoost, etc., although with advantageous features.
Historically, the first working neural network architecture is a multi-layer perceptron. It consists of layers, and each layer consists of neurons. The signal is transmitted in one direction - from the first layer to the last, and each neuron of the current layer is connected with all the neurons of the previous one, and with different weights. The weight of the connection between two neurons has a physical meaning of its importance: the greater its value, the greater the contribution to the output value of the neuron. To teach a neural network means to find such weights so that we can get what we need on the output layer.
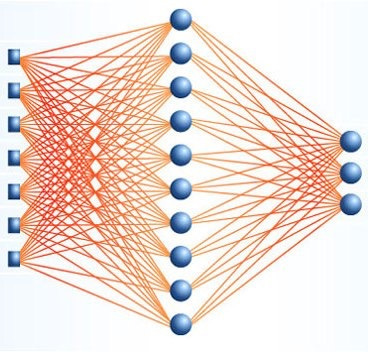
The fully connected architectures do not qualitatively differ from the classical methods: they take a vector of numbers as input, somehow they are processed, and the output is a set of probabilities that the input vector belongs to one of the classes (this is the case for the classification task, but others can be considered). In practice, other architectures (convolutional, recurrent) are used to process the input features, obtaining the so-called high-level features, and then process them using fully connected layers.
Analysis of the work of convolutional networks can be found here and here (there are thousands of them, so we leave the choice to the reader), and we will analyze the recurrent ones separately. At the input, they take sequences of numbers, no matter whether they are signs, signal values, or word labels. The role of neurons for them is usually performed by special cells, which, in addition to summing the input signal and receiving the output signal, have a set of additional parameters — internal values that are remembered and affect the output value of the cell.
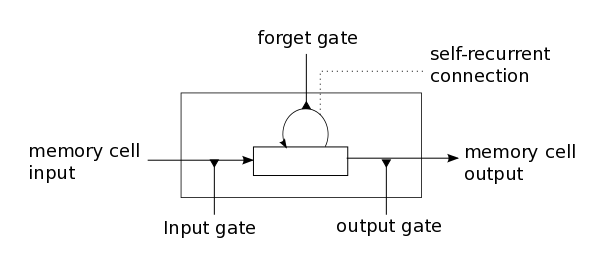
Today the most widely used recurrent architecture is Long Short-Term Memory (LSTM). In the simplest implementation, each cell contains three specific elements: input, output, and forgetting valve. They determine the proportions in which the processed input data and stored values need to be “mixed” in order to get the most useful signal at the output. To teach an LSTM network is to find the parameters of the valves and the weight of connections between the LSTM cells on the first layers and the neurons of the last layers, for which the output layer for the input sequence would return the probabilities of belonging to each of the classes.
We hope that you have read the first part of this guide. In it you can find a description of the speech base, the calculated signs, as well as the results of the work of the Random Forest classifier. He studied at the statistics of signs counted on good (up to a certain limit) filtered sections of speech - frames. For each characteristic, the mean, median, minimum and maximum values, as well as the standard deviation were considered.
Neural networks are more demanding on the number of training examples. In the last part, we studied 436 audio fragments from 109 speakers (four utterances for each) taken from the VCTK base. It turned out that none of the neural network architectures we tested could learn to reasonable accuracy values, and we took more fragments — a total of 5000. However, the increased sample did not lead to a significant increase in accuracy — 98.5% of correctly classified fragments. The first experiment we want to perform is to train a fully connected neural network on the same set of features.
We continue to write all the code in Python, we take the implementation of neural networks from Keras - the most convenient library, through which you can implement the necessary architectures in a couple of lines.
We import everything that we need:
We take the implementation of the random forest from sklearn, and from there, cross-validation into groups. From Keras, we take the base class for the models, the layers, the Bidirectional wrapper, which allows the use of bidirectional LSTM, as well as the to_categorical function encoding class labels in one-hot vector.
We read all the data:
And get a sample:
Here we applied filtering by frequency — we threw out from consideration those sections of speech where the pitch frequency was not determined. This can happen in two cases: the frame does not correspond to speech in general, or corresponds to consonant sounds or whispers. In our task, we can throw out absolutely all frames without a pitch, but in many others, filtering should be done less greedily.
Next you need to implement a fully connected neural network:
The first layer of the network is Batch Normalization . It eliminates the need to normalize the data, and also speeds up the learning process and makes it possible to avoid retraining to some extent. Initially, each batch (a portion of data at each iteration of training) is normalized to its own mean and standard deviations, and then scaled using a linear transformation, the parameters of which are to be optimized.
Approximately for the same purpose, after each fully connected layer, there are Dropout layers. They randomly select some of the neurons (in our case, half) of the previous layer and reset their output values. This makes the network more stable: even if we remove some of the links, it will still give the correct answer. Exactly for this reason, in practice, layers with double the number of neurons and a 50% dropout are more effective than ordinary layers.
Dense - directly full mesh layers. Their outputs are a classical weighted sum of input signals with some weights, which is nonlinearly transformed using the activation function. On the first layers, this is tanh , and on the last, softmax , so that the sum of the output signal equals one and corresponds to the probability of being in one of the classes. Model checkpoint is rather a decorative thing, rewriting a model after each training epoch, only if the error measure on the test sample — the validation loss — is less than the previous saved model. This ensures that the most efficient model is recorded in model.weights .
It remains to describe the process of cross-validation of the speakers and compare the fully connected network and the random forest described above on the same data:
We obtained approximately the same accuracy values - 98.6% for a random forest and 98.7% for a neural network. Probably, you can optimize the parameters and get higher accuracy, but immediately proceed to what it was all about: recurrent networks.
First you need to make a sample of the sequences. Keras, despite its simplicity, is sometimes fastidious, and here it is necessary that the input variables in the .fit or .fit_on_batch methods can be naturally transformed into tensors. For example, sequences of different lengths (and we have this particular case) do not possess this property.
This purely technical limitation of the library can be circumvented in several ways. The first is training in batch size 1. The obvious disadvantages of this approach are the inapplicability of batch normalization and the catastrophic increase in training time.
The second way is to add zeros to the sequence (padding) to get the desired dimension. At first glance, this seems wrong, but the network learns not to respond to such values. Also, these methods can be combined - to split the length of the sequence into several groups, inside each hold a padding and train.
We consider sequences of length 100 — this corresponds to one second of speech. To do this, we cut the long sequences in such a way that exactly 100 points remain, moreover, symmetrical with respect to the middle, and short ones with zeroes at the beginning and end to the desired length.
Bidirectional wrapper using merge_mode glues the outputs of the argument layer for the normal input sequence and in the reverse order. In our case, this is an LSTM layer with 100 cells. The return_sequences flag determines whether a sequence of internal cell states will be returned, or only the last one will return.
Inside LSTM and after the recurrent layers, a dropout is applied, and after the last layer (with return_sequences = False ), there is a softmax activation function. Also, the model is compiled with the Rmsprop optimizer - a modification of the stochastic gradient descent. In practice, it often turns out that it works better for recurrent networks, although this is not strictly proven and can always be different.
Hooray! 99.1% of correctly classified points per 5-fold cross-validation by speakers. This is the best result among all considered architectures.
The lion's share of machine learning guides, articles and popular science materials are devoted to image recognition. Very rarely - training with reinforcements. More rarely - audio processing. Partly, probably, this is due to the fact that out-of-the-box methods for audio processing do not work, and one has to spend his time on understanding processes, data preprocessing and other inevitable iterations. But it is precisely the complexity that makes the task interesting.
Gender recognition seems to be a simple task, because a person copes with it almost unmistakably. But its solution by the methods of machine learning "in the forehead" demonstrates an accuracy of about 70%, which is objectively not enough. However, even simple algorithms can achieve an accuracy of about 97-98%, if you do everything right: for example, filter the source data. Complex neural network approaches increase accuracy to more than 99%, which is hardly fundamentally different from human performance.
In fact, the potential of recurrent neural networks in this article is not fully disclosed. Even for the classification task (many to one) they can be used more efficiently. But of course, we will not do this yet. We offer readers to do without filtering frames, allowing the network to learn how to process only the necessary frames, and consider longer (either shorter or thinned) sequences.
Worked on the material:
Stay with us.
In the second part of the guide, we will see if neural networks can cope with this task more effectively than a random forest, and also try to take into account the biggest drawback of classical methods - the inability to work with data sequences.
In a sense, this stage is redundant: the sex of a person does not change during a conversation (at least at the current stage of development and under the specified standard conditions), therefore, it is not worth counting on an increase in accuracy. But for academic purposes, we will try.
')
 / Photograph by Tristan Bowersox / CC-SA
/ Photograph by Tristan Bowersox / CC-SAAnother chapter on how neural networks work
It is believed that the artificial neural network (neural network) is a mathematical model of the human brain. Actually, no : 50-60 years ago, biologists at a certain level studied the electrical processes in the brain, and mathematicians created a simplified model and programmed it.
It turned out that such structures are able to solve some simple problems, but a) worse than classical methods and b) much slower than them. And the undisputed status quo persisted for half a century - scientists developed a theory (teaching methods, architectures, fundamental mathematical questions), and computer hardware and software developed so that it became possible to solve some problems on a home PC at the world level.
But not everything is so smooth: a neuronet can learn to distinguish a cheetah from a leopard, and can consider one of these animals a spotted sofa. In addition, the processes of teaching a person and a machine are different: a computer needs thousands of teaching examples, while a person needs several. Obviously, the work of artificial neural networks is not very similar to human thinking, and they are not a computer model of the brain, but just another class of models in the list: Random Forest, SVM, XGBoost, etc., although with advantageous features.
Historically, the first working neural network architecture is a multi-layer perceptron. It consists of layers, and each layer consists of neurons. The signal is transmitted in one direction - from the first layer to the last, and each neuron of the current layer is connected with all the neurons of the previous one, and with different weights. The weight of the connection between two neurons has a physical meaning of its importance: the greater its value, the greater the contribution to the output value of the neuron. To teach a neural network means to find such weights so that we can get what we need on the output layer.

The fully connected architectures do not qualitatively differ from the classical methods: they take a vector of numbers as input, somehow they are processed, and the output is a set of probabilities that the input vector belongs to one of the classes (this is the case for the classification task, but others can be considered). In practice, other architectures (convolutional, recurrent) are used to process the input features, obtaining the so-called high-level features, and then process them using fully connected layers.
Analysis of the work of convolutional networks can be found here and here (there are thousands of them, so we leave the choice to the reader), and we will analyze the recurrent ones separately. At the input, they take sequences of numbers, no matter whether they are signs, signal values, or word labels. The role of neurons for them is usually performed by special cells, which, in addition to summing the input signal and receiving the output signal, have a set of additional parameters — internal values that are remembered and affect the output value of the cell.
Today the most widely used recurrent architecture is Long Short-Term Memory (LSTM). In the simplest implementation, each cell contains three specific elements: input, output, and forgetting valve. They determine the proportions in which the processed input data and stored values need to be “mixed” in order to get the most useful signal at the output. To teach an LSTM network is to find the parameters of the valves and the weight of connections between the LSTM cells on the first layers and the neurons of the last layers, for which the output layer for the input sequence would return the probabilities of belonging to each of the classes.

Initial settings
We hope that you have read the first part of this guide. In it you can find a description of the speech base, the calculated signs, as well as the results of the work of the Random Forest classifier. He studied at the statistics of signs counted on good (up to a certain limit) filtered sections of speech - frames. For each characteristic, the mean, median, minimum and maximum values, as well as the standard deviation were considered.
Neural networks are more demanding on the number of training examples. In the last part, we studied 436 audio fragments from 109 speakers (four utterances for each) taken from the VCTK base. It turned out that none of the neural network architectures we tested could learn to reasonable accuracy values, and we took more fragments — a total of 5000. However, the increased sample did not lead to a significant increase in accuracy — 98.5% of correctly classified fragments. The first experiment we want to perform is to train a fully connected neural network on the same set of features.
We continue to write all the code in Python, we take the implementation of neural networks from Keras - the most convenient library, through which you can implement the necessary architectures in a couple of lines.
We import everything that we need:
import csv, os import numpy as np import sklearn from sklearn.ensemble import RandomForestClassifier as RFC from sklearn.model_selection import GroupKFold from keras.models import Model from keras.callbacks import ModelCheckpoint from keras.layers import Input, Dense, Dropout, LSTM, Activation, BatchNormalization from keras.layers.wrappers import Bidirectional from keras.utils import to_categorical We take the implementation of the random forest from sklearn, and from there, cross-validation into groups. From Keras, we take the base class for the models, the layers, the Bidirectional wrapper, which allows the use of bidirectional LSTM, as well as the to_categorical function encoding class labels in one-hot vector.
We read all the data:
with open('data.csv', 'r')as c: r = csv.reader(c, delimiter=',') header = next(r) data = [] for row in r: data.append(row) data = np.array(data) genders = data[:, 0].astype(int) speakers = data[:, 1].astype(int) filenames = data[:, 2] times = data[:, 3].astype(float) pitch = data[:, 4:5].astype(float) features = data[:, 4:].astype(float) And get a sample:
def make_sample(x, y, subj, names, statistics=[np.mean, np.std, np.median, np.min, np.max]): avx = [] avy = [] avs = [] keys = np.unique(names) for ki, k in enumerate(keys): idx = names == k v = [] for stat in statistics: v += stat(x[idx], axis=0).tolist() avx.append(v) avy.append(y[idx][0]) avs.append(subj[idx][0]) return np.array(avx), np.array(avy).astype(int), np.array(avs).astype(int) filter_idx = pitch[:, 0] > 1 filtered_average_features, filtered_average_genders, filtered_average_speakers = make_sample(features[filter_idx], genders[filter_idx], speakers[filter_idx], filenames[filter_idx]) Here we applied filtering by frequency — we threw out from consideration those sections of speech where the pitch frequency was not determined. This can happen in two cases: the frame does not correspond to speech in general, or corresponds to consonant sounds or whispers. In our task, we can throw out absolutely all frames without a pitch, but in many others, filtering should be done less greedily.
Next you need to implement a fully connected neural network:
def train_dnn(x, y, tx, ty): yc = to_categorical(y) # one-hot encoding for y tyc = to_categorical(ty)# one-hot encoding for y_test inp = Input(shape=(x.shape[1],)) model = BatchNormalization()(inp) model = Dense(100, activation='tanh')(model) model = Dropout(0.5)(model) model = Dense(100, activation='tanh')(model) model = Dropout(0.5)(model) model = Dense(100, activation='sigmoid')(model) model = Dense(2, activation='softmax')(model) model = Model(inputs=[inp], outputs=[model]) model.compile(optimizer='sgd', loss='categorical_crossentropy', metrics=['acc']) modelcheckpoint = ModelCheckpoint('model.weights', monitor='val_loss', verbose=1, save_best_only=True, mode='min') model.fit(x, yc, validation_data=(tx, tyc), epochs=100, batch_size=100, callbacks=[modelcheckpoint], verbose=2) model.load_weights('model.weights') return model The first layer of the network is Batch Normalization . It eliminates the need to normalize the data, and also speeds up the learning process and makes it possible to avoid retraining to some extent. Initially, each batch (a portion of data at each iteration of training) is normalized to its own mean and standard deviations, and then scaled using a linear transformation, the parameters of which are to be optimized.
Approximately for the same purpose, after each fully connected layer, there are Dropout layers. They randomly select some of the neurons (in our case, half) of the previous layer and reset their output values. This makes the network more stable: even if we remove some of the links, it will still give the correct answer. Exactly for this reason, in practice, layers with double the number of neurons and a 50% dropout are more effective than ordinary layers.
Dense - directly full mesh layers. Their outputs are a classical weighted sum of input signals with some weights, which is nonlinearly transformed using the activation function. On the first layers, this is tanh , and on the last, softmax , so that the sum of the output signal equals one and corresponds to the probability of being in one of the classes. Model checkpoint is rather a decorative thing, rewriting a model after each training epoch, only if the error measure on the test sample — the validation loss — is less than the previous saved model. This ensures that the most efficient model is recorded in model.weights .
It remains to describe the process of cross-validation of the speakers and compare the fully connected network and the random forest described above on the same data:
def subject_cross_validation(clf, x, y, subj, folds): gkf = GroupKFold(n_splits=folds) scores = [] for train, test in gkf.split(x, y, groups=subj): if clf == 'dnn': model = train_dnn(x[train], y[train], x[test], y[test]) score = model.evaluate(x[test], to_categorical(y[test]))[1] scores.append(score) elif clf == 'lstm': model = train_lstm(x[train], y[train], x[test], y[test]) score = model.evaluate(x[test], to_categorical(y[test]))[1] scores.append(score) else: clf.fit(x[train], y[train]) scores.append(clf.score(x[test], y[test])) return np.mean(scores) score_filtered = subject_cross_validation(RFC(n_estimators=1000), filtered_average_features, filtered_average_genders, filtered_average_speakers, 5) print score_filtered score_filtered = subject_cross_validation('dnn', filtered_average_features, filtered_average_genders, filtered_average_speakers, 5) print('Utterance classification an averaged features over filtered frames, accuracy:', score_filtered) We obtained approximately the same accuracy values - 98.6% for a random forest and 98.7% for a neural network. Probably, you can optimize the parameters and get higher accuracy, but immediately proceed to what it was all about: recurrent networks.
def make_sequences(x, y, subj, names): sx = [] sy = [] ss = [] keys = np.unique(names) sequence_length = 100 for ki, k in enumerate(keys): idx = names == k v = x[idx] w = np.zeros((sequence_length, v.shape[1]), dtype=float) sh = v.shape[0] if sh <= sequence_length: dh = sequence_length - sh if dh % 2 == 0: w[dh//2:sequence_length-dh//2, :] = v else: w[dh//2:sequence_length-1-dh//2, :] = v else: dh = sh - sequence_length w = v[sh//2-sequence_length//2:sh//2+sequence_length//2, :] sx.append(w) sy.append(y[idx][0]) ss.append(subj[idx][0]) return np.array(sx), np.array(sy).astype(int), np.array(ss).astype(int) First you need to make a sample of the sequences. Keras, despite its simplicity, is sometimes fastidious, and here it is necessary that the input variables in the .fit or .fit_on_batch methods can be naturally transformed into tensors. For example, sequences of different lengths (and we have this particular case) do not possess this property.
This purely technical limitation of the library can be circumvented in several ways. The first is training in batch size 1. The obvious disadvantages of this approach are the inapplicability of batch normalization and the catastrophic increase in training time.
The second way is to add zeros to the sequence (padding) to get the desired dimension. At first glance, this seems wrong, but the network learns not to respond to such values. Also, these methods can be combined - to split the length of the sequence into several groups, inside each hold a padding and train.
We consider sequences of length 100 — this corresponds to one second of speech. To do this, we cut the long sequences in such a way that exactly 100 points remain, moreover, symmetrical with respect to the middle, and short ones with zeroes at the beginning and end to the desired length.
def train_lstm(x, y, tx, ty): yc = to_categorical(y) tyc = to_categorical(ty) inp = Input(shape=(x.shape[1], x.shape[2])) model = BatchNormalization()(inp) model = Bidirectional(LSTM(100, return_sequences=True, recurrent_dropout=0.1), merge_mode='concat')(model) model = Dropout(0.5)(model) model = Bidirectional(LSTM(100, return_sequences=True, recurrent_dropout=0.1), merge_mode='concat')(model) model = Dropout(0.5)(model) model = Bidirectional(LSTM(2, return_sequences=False, recurrent_dropout=0.1), merge_mode='ave')(model) model = Activation('softmax')(model) model = Model(inputs=[inp], outputs=[model]) model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['acc']) modelcheckpoint = ModelCheckpoint('model.weights', monitor='val_loss', verbose=1, save_best_only=True, mode='min') model.fit(x, yc, validation_data=(tx, tyc), epochs=100, batch_size=50, callbacks=[modelcheckpoint], verbose=2) model.load_weights('model.weights') return model Bidirectional wrapper using merge_mode glues the outputs of the argument layer for the normal input sequence and in the reverse order. In our case, this is an LSTM layer with 100 cells. The return_sequences flag determines whether a sequence of internal cell states will be returned, or only the last one will return.
Inside LSTM and after the recurrent layers, a dropout is applied, and after the last layer (with return_sequences = False ), there is a softmax activation function. Also, the model is compiled with the Rmsprop optimizer - a modification of the stochastic gradient descent. In practice, it often turns out that it works better for recurrent networks, although this is not strictly proven and can always be different.
filter_idx = pitch[:, 0] > 1 filtered_sequences_features, filtered_sequences_genders, filtered_sequences_speakers = make_sequences(features[filter_idx], genders[filter_idx], speakers[filter_idx], filenames[filter_idx]) score_lstmfiltered = subject_cross_validation('lstm', filtered_sequences_features, filtered_sequences_genders, filtered_sequences_speakers, 5) print score_lstm_filtered Hooray! 99.1% of correctly classified points per 5-fold cross-validation by speakers. This is the best result among all considered architectures.
Conclusion
The lion's share of machine learning guides, articles and popular science materials are devoted to image recognition. Very rarely - training with reinforcements. More rarely - audio processing. Partly, probably, this is due to the fact that out-of-the-box methods for audio processing do not work, and one has to spend his time on understanding processes, data preprocessing and other inevitable iterations. But it is precisely the complexity that makes the task interesting.
Gender recognition seems to be a simple task, because a person copes with it almost unmistakably. But its solution by the methods of machine learning "in the forehead" demonstrates an accuracy of about 70%, which is objectively not enough. However, even simple algorithms can achieve an accuracy of about 97-98%, if you do everything right: for example, filter the source data. Complex neural network approaches increase accuracy to more than 99%, which is hardly fundamentally different from human performance.
In fact, the potential of recurrent neural networks in this article is not fully disclosed. Even for the classification task (many to one) they can be used more efficiently. But of course, we will not do this yet. We offer readers to do without filtering frames, allowing the network to learn how to process only the necessary frames, and consider longer (either shorter or thinned) sequences.
Worked on the material:
- Gregory Sterling , mathematician, leading expert of the Neurodata Lab on machine learning and data analysis
- Eva Kazimirova , biologist, physiologist, expert of the Neurodata Lab in the field of acoustics, voice and speech analysis
Stay with us.
Source: https://habr.com/ru/post/335804/
All Articles