This article is an adaptation of sections 2 and 3 of chapter 9 of my book, Depth Learning with Python (Manning Publications).

The article is intended for people who already have significant experience with deep learning (for example, those who have already read chapters 1-8 of this book). A large amount of knowledge is assumed.

---

Limitations of depth learning

Deep learning: geometric look

The most amazing thing about depth learning is how simple it is. Ten years ago, no one could imagine what amazing results we would achieve in problems of machine perception using simple parametric models trained with a gradient descent. Now it turns out that we need only sufficiently large parametric models, trained on a sufficiently large number of samples. As Feynman once said about the Universe: “ It’s not complicated, there’s just a lot of it.”

In depth learning, everything is a vector, that is, a point in geometric space . The input data of the model (it can be text, images, etc.) and its goals are first “vectorized”, that is, they are translated into a kind of initial vector space at the input and the target vector space at the output. Each layer in the depth learning model performs one simple geometric transformation of the data that goes through it. Together, the chain of layers of the model creates one very complex geometric transformation, broken down into a series of simple ones. This complex transformation attempts to transform the input data space into the target space, for each point. The transformation parameters are determined by the layer weights, which are constantly updated based on how well the model works at the moment. The key characteristic of a geometric transformation is that it must be differentiable , that is, we must be able to know its parameters through a gradient descent. Intuitively, this means that geometric morphing should be smooth and continuous - an important limitation.
')
The entire process of applying this complex geometric transformation on the input data can be visualized in 3D, depicting a person who is trying to unfold a paper ball: a crumpled paper ball is a variety of input data with which the model begins to work. Every movement of a person with a paper ball is like a simple geometric transformation that one layer performs. The complete sequence of gestures for unfolding is a complex transformation of the entire model. Depth learning models are mathematical machines for unfolding an intricate variety of multidimensional data.

This is what the magic of depth learning is: transform a value into vectors, into geometric spaces, and then gradually learn complex geometric transformations that transform one space into another. All that is needed is spaces of sufficiently large dimension to convey the full range of relationships found in the source data.

Limitations of depth learning

The set of tasks that can be solved with this simple strategy is almost endless. Still, many of them are still beyond the reach of current in-depth training techniques — even though there is a huge amount of manually annotated data. Let's say, for example, that you can collect a set of data from hundreds of thousands — even millions — of descriptions in English of the software features written by product managers, as well as the corresponding source year developed by teams of engineers to meet these requirements. Even with this data, you cannot train the depth learning model to simply read the product description and generate the corresponding code base. This is just one of many examples. In general, everything that requires argumentation, reasoning - like programming or using a scientific method, long-term planning, manipulating data in an algorithmic style - is beyond the capabilities of depth learning models, no matter how much data you throw at them. Even learning the neural network to sort the algorithm is an incredibly difficult task.

The reason is that the depth learning model is “only” a chain of simple, continuous geometric transformations that transform one vector space into another. All it can do is convert one set of X data into another Y set, provided there is a possible continuous transformation from X to Y that can be learned and the availability of a dense set of X: Y transformation patterns as data for training. So, although the depth learning model can be considered a type of program, most programs cannot be expressed as depth learning models — for most tasks, either there is no deep neural network of practically suitable size that solves the problem, or if it does, it can be unteachable , that is the conversion may be too complicated, or there is no suitable data for its training.

Scaling up existing depth learning techniques — adding more layers and using more data for training — can only superficially alleviate some of these problems. It will not solve the more fundamental problem that depth learning models are very limited in what they can represent, and that most programs cannot be expressed in the form of continuous geometric morphing of a variety of data.

The risk of anthropomorphizing machine learning models

One of the very real risks of modern AI is the misinterpretation of the work of deep learning models and the exaggeration of their capabilities. The fundamental feature of the human mind is the “model of the human psyche”, our tendency to project goals, beliefs and knowledge on the surrounding things. The drawing of a smiling face on a stone suddenly makes us “happy” - mentally. Attached to depth learning, this means, for example, that if we can more or less successfully train a model to generate textual descriptions of pictures, we tend to think that the model "understands" the content of the images, as well as the generated descriptions. We are then very surprised when, due to a small deviation from the set of images presented in the data for training, the model begins to generate absolutely absurd descriptions.



In particular, this is most clearly manifested in the “adversarial examples”, that is, the samples of the input data of the depth learning network, specially selected to be misclassified. You already know that you can make a gradient ascent in the input data space to generate patterns that maximize the activation of, for example, a certain convolutional neural network filter - this is the basis of the visualization technique that we discussed in Chapter 5 (note: the book “ Depth Learning with Python ”) , as well as the Deep Dream algorithm from Chapter 8. In a similar way, through a gradient ascent, you can slightly change the image to maximize the class prediction for a given class. If you take a photo of a panda and add a gibbon gradient, we can force the neural network to classify this panda as a gibbon. This demonstrates both the fragility of these models and the profound difference between the transformation from entrance to exit, which it is guided by, and our own human perception.



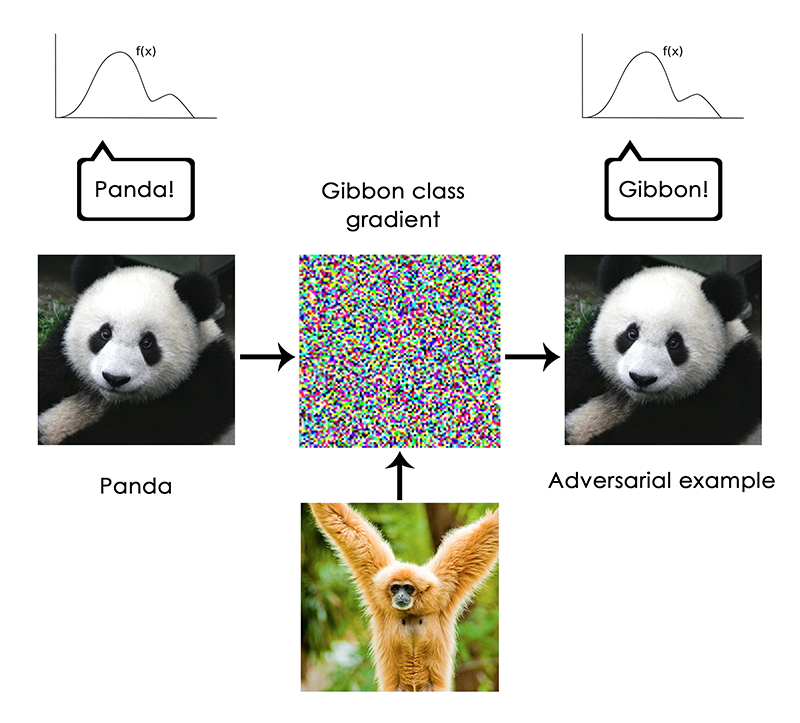
In general, depth learning models have no understanding of the input data, at least not in the human sense. Our own understanding of images, sounds, language, is based on our sensorimotor experience as humans - as material earthly creatures. Machine learning models do not have access to this experience and therefore cannot “understand” our input in any human-like way. By annotating a large number of learning examples for our models, we force them to learn the geometric transformation that leads the data to human concepts for this particular set of examples, but this transformation is only a simplified sketch of the original model of our mind, which is developed from our experience as bodily agents are like a weak reflection in a mirror.



As a machine learning practitioner, always remember this, and never fall into the trap of believing that neural networks understand the task they are performing - they do not understand, at least not in a way that makes sense to us. They were trained by a different, much more narrow task than the one we want to teach them: simple transformation of input learning patterns into target learning patterns, point to point. Show them something that is different from the training data, and they will break in the most absurd way.

Local generalization versus limit generalization

There seems to be a fundamental difference between direct geometric morphing from inlet to outlet, which is done by depth learning models and the way people think and learn. The point is not only that people themselves learn from their bodily experience, and not through the processing of a set of training samples. In addition to the difference in learning processes, there are fundamental differences in the nature of the underlying concepts.

People are capable of much more than transforming an immediate stimulus into an immediate response, like a neural network or maybe an insect. People hold in their minds complex, abstract models of the current situation, themselves, other people, and can use these models to predict various possible options for the future, and carry out long-term planning. They are capable of combining into one whole well-known concepts, in order to present what they have never known before - like drawing a horse in jeans, for example, or an image of what they would do if they won the lottery. The ability to think hypothetically, to expand our model of mental space far beyond what we directly experienced, that is, the ability to do abstractions and reasoning , perhaps, is the defining characteristic of human cognition. I call this “limiting generalization”: the ability to adapt to new, never-before-experienced situations, using very little data or not using any data at all.

This is very different from what deep learning networks do, which I would call a “local generalization”: the conversion of input data into output data quickly ceases to make sense if the new input data is at least slightly different from what they encountered during training . Consider, for example, the problem of learning the appropriate parameters of launching a rocket, which should land on the moon. If you used a neural network for this task, teaching it with a teacher or with reinforcement, you would need to give it thousands or millions of flight paths, that is, you need to give a dense set of examples in the space of input values ​​to learn how to reliably transform from the space of input values ​​into space outgoing values. In contrast, people can use the power of abstraction to create physical models - rocket science - and bring out the exact solution that will deliver the rocket to the moon in just a few attempts. In the same way, if you developed a neural network to control the human body and want it to learn how to safely pass through the city without being hit by a car, the network must die thousands of times in different situations before concluding that cars are dangerous and will not work appropriate behavior to avoid them. If she was transferred to a new city, then the network would have to re-learn most of what she knew. On the other hand, people are able to learn safe behavior without dying once - again, thanks to the power of abstract modeling of hypothetical situations.



So, despite our progress in machine perception, we are still very far from human-level AI: our models can perform only local generalization , adapting to new situations that should be very close to past data, while the human mind is capable of extreme generalization , quickly adapting to completely new situations or planning far into the future.

findings

Here's what you need to remember: the only real success of depth learning to date is the ability to translate space X into space Y, using continuous geometric transformation, with a large amount of data annotated by humans. A good accomplishment of this task is a revolutionary important achievement for the whole industry, but human-level AI is still very far away.

To remove some of these restrictions and begin to compete with the human brain, we need to move away from direct transformation from the entrance to the output and go to reasoning and abstractions . Perhaps a suitable basis for abstract modeling of various situations and concepts may be computer programs. We said earlier (note: in the book “ Depth Learning with Python ”) that machine learning models can be defined as “learning programs”; at the moment we can train only a narrow and specific subset of all possible programs. But what if we could train each program, modularly and repeatedly? Let's see how we can come to this.

Future depth learning

Given what we know about the work of depth learning networks, their limitations and the current state of scientific research, can we predict what will happen in the medium term? Here are a few of my personal thoughts on this. Keep in mind that I do not have a crystal ball for predictions, so much of what I expect may not be translated into reality. This is absolute speculation. I share these predictions not because I expect them to be fully embodied in the future, but because they are interesting and applicable in the present.

At a high level, here are the main areas that I consider promising:

• The models will approach the general purpose computer programs, built on top of much richer primitives than our current differentiated layers - so we get reasoning and abstractions , the absence of which is the fundamental weakness of the current models.
• New forms of learning will appear that will make this possible — and allow models to simply move away from differentiated transformations.
• Models will require less developer involvement - it should not be your job to constantly twist the handles.
• A larger, systematic reuse of learned features and architectures will appear; meta-learning systems based on reusable and modular routines.

In addition, note that these considerations are not specifically related to teacher training, which still remains the basis of machine learning — they also apply to any form of machine learning, including unsupervised learning, supervised learning, and reinforcement learning. It is fundamentally irrelevant where your tags came from or what your training cycle looks like; these different branches of machine learning are just different facets of the same design.

So, go ahead.

Models as programs

As we noted earlier, the necessary transformational development that can be expected in the field of machine learning is a departure from models that perform pure pattern recognition and are only capable of local generalization , models that are capable of abstraction and reasoning , which can reach the limit of generalization . All current AI programs with a basic level of reasoning are rigidly programmed by human programmers: for example, programs that rely on search algorithms, graph manipulations, formal logic. Thus, in the DeepMind AlphaGo program, most of the “intelligence” on the screen is designed and rigidly programmed by expert programmers (for example, a Monte Carlo search in the tree); training on new data takes place only in specialized sub-modules — value network and policy network. But in the future, such AI systems can be fully trained without human participation.

How to achieve this? Take the well-known type of network: RNN. What is important, RNN has fewer restrictions than direct distribution neural networks. This is because RNNs are slightly larger than simple geometric transformations: these are geometric transformations that are carried out continuously in the for loop . The for loop is given by the developer: this is the built-in assumption of the network. Naturally, RNN networks are still limited in that they can represent, basically, because their every step is still a differentiable geometric transformation and because of the way they pass information step by step through points in a continuous geometric space ( state vectors). Now imagine neural networks that would be “extended” by programming primitives in the same way as for loops — but not just with a single hard-coded for loop with stitched geometric memory, but with a large set of programming primitives with which the model could freely turn to expand its processing capabilities, such as branches of if , operators while , creating variables, disk storage for long-term memory, sorting operators, advanced data structures such as lists, graphs, hash Table IC, and more. The space of programs that such a network can represent will be much wider than existing depth learning networks can express, and some of these programs can achieve an excellent generalization force.

In a word, we will get away from the fact that on the one hand we have “hard-coded algorithmic intelligence” (hand-written software), and on the other hand, “trained geometric intelligence” (deep learning). Instead, we get a mixture of formal algorithmic modules that provide reasoning and abstraction capabilities, and geometric modules that provide opportunities for informal intuition and pattern recognition . The entire system will be fully trained with little or no human participation.

A related field of AI, which, in my opinion, may soon move forward greatly, is software synthesis , in particular, neural software synthesis. Software synthesis consists in the automatic generation of simple programs using a search algorithm (possibly genetic search, as in genetic programming) to study a large space of possible programs. The search stops when a program is found that meets the required specifications, often provided as a set of I / O pairs. As you can see, this is very much like machine learning: “learning data” is provided as input-output pairs, we find a “program” that corresponds to the transformation of the input to the output data and is capable of generalizations for new input data. The difference is that instead of learning values ​​in a hard-coded program (neural network), we generate the source code through a discrete search process.

I definitely expect that there will be a lot of interest in this area again in the next few years. In particular, I expect the mutual penetration of related areas of deep learning and program synthesis, where we will not just generate programs in general-purpose languages, but where we will generate neural networks (processing of geometric data), complemented by a rich set of algorithmic primitives, such as for cycles - and many others. It should be much more convenient and useful than the direct generation of source code, and significantly expand the boundaries for those problems that can be solved with the help of machine learning - the space of programs that we can generate automatically, obtaining relevant data for training. A mixture of symbolic AI and geometric AI. Modern RNN can be considered as the historical ancestor of such hybrid algorithm-geometric models.


Figure: A trained program simultaneously relies on geometric primitives (pattern recognition, intuition) and algorithmic primitives (argumentation, search, memory).

Beyond backpropagation and differentiated layers

If machine learning models become more like programs, then they will no longer be differentiable - definitely, these programs will still use continuous geometric layers as subroutines that will remain differentiable, but the whole model will not be like that. As a result, the use of back propagation to tune the weights in a fixed, hard-coded network cannot remain the preferred method for training models in the future — at least it cannot be limited to this method. We need to figure out how to most effectively train undifferentiable systems. Current approaches include genetic algorithms, “evolutionary strategies”, certain reinforcement learning methods, ADMM (the Lagrange multipliers alternating direction method). Naturally, the gradient descent will not go anywhere else - information about the gradient will always be useful for optimizing differentiable parametric functions. But our models will definitely become more ambitious than simply differentiable parametric functions, and therefore their automated development (“training” in “machine learning”) will require more than back propagation.

In addition, backward propagation has an end-to-end framework, which is suitable for learning good concatenated transformations, but is rather inefficient from a computational point of view, because it does not fully utilize the modularity of the deep networks. To increase the effectiveness of anything, there is one universal recipe: to introduce modularity and hierarchy. So we can make the reverse propagation itself more efficient by introducing disconnected learning modules with a specific synchronization mechanism between them, organized hierarchically. This strategy is partly reflected in DeepMind's recent work on "synthetic gradients." I expect much, much more work in this direction in the near future.

One can imagine a future where globally non-differentiable models (but with differentiated parts) will be trained — grow — using an efficient search process that will not apply gradients, while differentiable parts will learn even faster using gradients using some more efficient back distribution versions

Automated Machine Learning

In the future, architectures of the model will be created by training, and not written by hand by engineers. Learning models automatically work together with a richer set of primitives and program-like machine learning models.

Most of the time now, the developer of depth learning systems infinitely modifies the data with Python scripts, then long sets up the architecture and hyperparameters of the depth learning network to get a working model — or even to get an outstanding model if the developer is so ambitious. Needless to say, this is not the best state of things. But AI can help here. Unfortunately, the part of processing and preparing data is difficult to automate, because it often requires knowledge of the field, as well as a clear understanding at a high level, what the developer wants to achieve. However, setting up hyper parameters is a simple search procedure, and in this case we already know what the developer wants to achieve: this is determined by the loss function of the neural network that needs to be configured. It has become a common practice to install basic AutoML systems that take over most of the model's spin-ups. I myself installed one to win the Kaggle competition.

At the most basic level, such a system will simply adjust the number of layers in the stack, their order and the number of elements or filters in each layer. This is usually done using libraries like Hyperopt, which we discussed in Chapter 7 (note: the book “ Depth Learning with Python ”). But you can go much further and try to get the appropriate architecture from scratch, with a minimum set of restrictions. This is possible through reinforcement training, for example, or through genetic algorithms.

Another important direction in the development of AutoML is getting the model architecture learning at the same time as model weights. Teaching the model from scratch every time we try slightly different architectures, which is extremely inefficient, so a really powerful AutoML system will manage the development of architectures, while the properties of the model are tuned back to the data for training, thus eliminating all the excessive calculations. When I write these lines, similar approaches have already begun to be applied.

When all this starts to happen, the developers of machine learning systems will not remain without work - they will move to a higher level in the value chain. They will begin to put far more effort into creating complex loss functions that truly reflect business objectives, and will deeply understand how their models affect the digital ecosystems in which they work (for example, customers who use model predictions and generate data for her training) - problems that only the largest companies can afford to consider now.

Lifelong learning and reuse of modular routines

If models become more complex and are built on richer algorithmic primitives, then this increased complexity will require more intensive reuse between tasks, rather than learning the model from scratch every time we have a new task or a new data set. In the end, many data sets do not contain enough information to develop from scratch a new complex model and it will just be necessary to use information from previous data sets. You do not learn English again every time you open a new book - it would be impossible. In addition, learning models from scratch on each new task is very inefficient due to the significant overlap between current tasks and those encountered before.

In addition, in recent years, a remarkable observation has repeatedly sounded that learning the same model to do several loosely coupled tasks improves its results in each of these tasks . For example, learning the same neural network to translate from English to German and from French to Italian will result in a model that will be better in each of these language pairs. Teaching an image classification model simultaneously with an image segmentation model, with a single convolutional base, will result in a model that is better in both tasks. And so on. This is quite intuitive: there is always some information that overlaps between these two seemingly different tasks, and therefore the general model has access to more information about each individual task than a model that has been trained only on this particular task.

What we actually do when we reapply the model on different tasks is to use the pre-learned weights for models that perform common functions, such as extracting visual signs. You have seen this in practice in chapter 5. I expect that in the future a more general version of this technique will be used everywhere: we will not only use the previously learned features (sub-model weights), but also model architectures and training procedures. As models become more similar to programs, we will begin to reuse subroutines , like functions and classes in ordinary programming languages.

Think about how the software development process looks today: as soon as the engineer solves a particular problem (HTTP requests in Python, for example), it packs it as an abstract library for reuse. Engineers who will encounter a similar problem in the future are simply looking for existing libraries, downloading and using them in their own projects. In the same way, in the future, meta-learning systems will be able to assemble new programs by sifting through the global library of high-level reusable blocks. If the system starts developing similar subroutines for several different tasks, it will release an “abstract” reusable version of the subroutine and save it in the global library. Such a process will open up the possibility for abstraction , a necessary component for achieving “ultimate generalization”: a subroutine that will be useful for many tasks and areas can be said to “abstract” some aspect of decision making. Such a definition of "abstraction" does not seem to be the concept of abstraction in software development. These routines can be either geometric (depth learning modules with pre-trained views), or algorithmic (closer to the libraries that modern programmers work with).



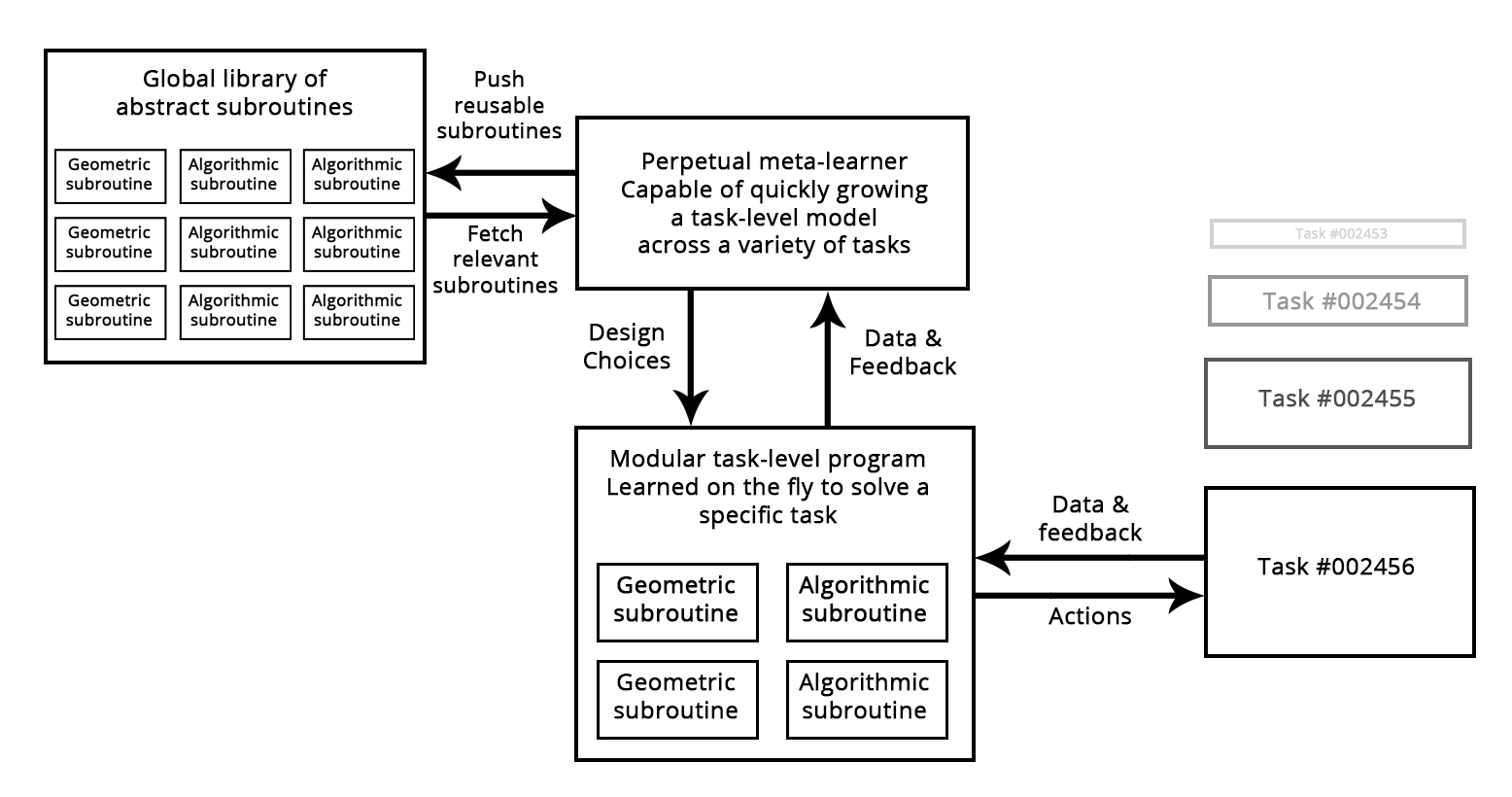
Figure: A meta-learning system that is able to quickly develop task-specific models using reusable primitives (algorithmic and geometric), thereby achieving a “limit generalization”.

The bottom line: long-term vision

In short, here is my long-term vision for machine learning:

• The models will become more like programs and get opportunities that extend far beyond the limits of continuous geometric transformations of the original data, with which we are working now. Perhaps these programs will be much closer to the abstract mental models that people support about their surroundings and about themselves, and they will be capable of a stronger generalization due to their algorithmic nature.
  
  
• In particular, the models will mix algorithmic modules with formal reasoning, searching, abstraction abilities - and geometric modules with informal intuition and pattern recognition. AlphaGo (a system that required intensive manual programming and architecture development) is an early example of what a combination of symbolic and geometric AI might look like.
  
  
• They will be grown automatically (and not manually written by human programmers) using modular parts from the global reusable subroutine library — a library that evolved by mastering high-performance models from thousands of previous tasks and data sets. Once the meta-learning system has identified common problem solving patterns, they are converted to reusable subroutines — much like the functions and classes in modern programming — and added to the global library. This is how abstraction is achieved.
  
  
• The global library and the corresponding model-growing system will be able to achieve some form of human-like “ultimate generalization”: faced with a new task, a new situation, the system will be able to assemble a new working model for this task, using a very small amount of data thanks to: 1) rich program-like primitives, which make generalizations well and 2) extensive experience in solving similar problems. In the same way that people can quickly learn a new, complex video game, because they have the previous experience of many other games and because models based on previous experience are abstract and program-like, rather than simply transforming the stimulus into action.
  
  
• Essentially, this continuously learning model-growing system can be interpreted as Strong Artificial Intelligence. But do not wait for the onset of some singular roboapocalypse: it is a pure fantasy, which was born from a large list of deep misunderstandings in understanding intelligence and technology. However, this criticism is not the place.