Geekly Articles each Day
📜 ⬆️ ⬇️

Introduction to octree



What is octree? If you absolutely do not know this concept, then I recommend reading the article on Wikipedia (it will take about five minutes). It gives a sufficient idea , but it will hardly be enough to understand what they are used for and how to implement them.

In this article I will try to talk about all the steps needed to create a data structure of oktotreev, using the example of explaining concepts, illustrations and code. I will also describe my decisions that I took at each of the stages. Do not think that this article will be the only correct guide to the implementation of oktotreev, but it should give you a good foundation and you can use it for reference.

Required knowledge


When writing this article, I assumed that the reader:
')
  1. Well versed in programming in a language with syntax in the style of C (I will use C # with XNA).
  2. Already programmed some tree data structure , for example, a binary search tree , is familiar with recursion, its strengths and weaknesses.
  3. Knows how collision detection with boundary rectangles, spheres and truncated pyramids is implemented.
  4. Understands in standard data structures (arrays, lists, etc.), he understands that there is such a big “O” (you can also read about the big “O” in this GDnet article ).
  5. Works on a project that has features that need collision checking.

Stage preparation


Suppose we create a very large-scale game in which thousands of physical objects of different types, shapes and sizes can be contained, and some of them must collide with each other. In each frame, we will have to determine which objects intersect with each other and somehow handle these intersections. How to do this so that the game speed does not fall?



Brute-force collision detection


The simplest solution is to compare each object with all objects in the world. This can usually be done in two for loops. The code will look something like this:

foreach(gameObject myObject in ObjList) { foreach(gameObject otherObject in ObjList) { if(myObject == otherObject) continue; //       if(myObject.CollidesWith(otherObject)) { //   } } }

Graphically, this can be represented as:



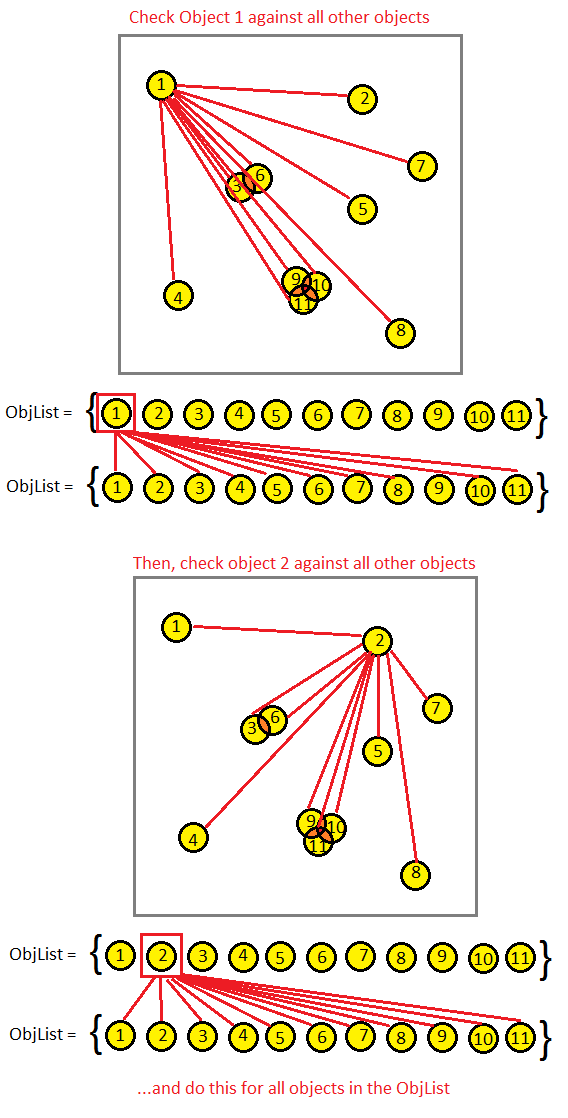
Each red line is a cost check for intersections in the CPU.

Naturally, such code should terrify you, because it will be executed O (N 2 ) times. If we have 10,000 objects, we will have to perform 100,000,000 collision checks (one hundred million). No matter how fast your processor is and how much you have improved the mathematical code - such a program will slow down in the computer. If the game works with 60 frames per second, then 60 * 100 million calculations will be performed per second! This is a complete insanity.

If this can be avoided, let's not do that, at least for large sets of objects. This will be acceptable only if, say, a check is performed for only 10 objects (100 checks). If you know in advance that there will be few objects in the game (for example, asteroids), then perhaps you can easily do a brute force and you can completely abandon the octree tree. If you start to notice performance problems due to too many collision checks per frame, you can use very simple optimizations:

1. How many calculations are required for your collision calculation procedure? Maybe the square root calculation is hidden somewhere in it (for example, in distance checking)? Do you perform detailed collision checking (intersection of pixels, triangles, etc.)? There is a standard technique: first perform a rough check of collisions, and then go to a more detailed one. You can add objects describing their rectangular or spherical boundary and check the intersection between the boundaries, and then perform a detailed test that requires more mathematical calculations and resources.

To compare the distances between objects, use the square check of the distance between objects to avoid calculating the square root. To calculate the square root, the approximation by the Newton method is usually used and it can be very costly.

2. Is it possible to do without calculating fewer collision checks? If the game runs at 60 frames per second, can I miss a few frames? If the behavior of some objects is deterministic, then their collisions can be calculated in advance (for example, between a billiard ball and a table board). Is it possible to reduce the number of objects for which the scan is performed? Try to split objects into different lists. In one list may be "stationary" objects. Their collisions between each other can never be checked. In the other list there can be “moving” objects for which it is necessary to check collisions with all other moving and all stationary objects. This can reduce the number of required collision checks to an acceptable level in terms of performance.

3. Is it possible to refuse to check the collisions of some objects when performance problems arise? For example, a particle of smoke can interact with a surface object and follow its contours to create a beautiful effect, but this should not interfere with the gameplay. If the number of checks exceeds a certain limit, then you can stop the calculation of collisions for smoke particles. However, ignoring the movement of important game objects will also destroy the gameplay (for example, player’s bullets will no longer interact with monsters). That is, it will be useful to keep a list of priorities for collision checks. First, collisions with a high priority are processed, and if the limit is not exceeded, then collisions with a low priority can be processed. When the limit is reached, the game must discard all remaining items in the priority list or postpone their check for the future.

4. Is it possible to use a faster, but still easy way to recognize collisions in order to get rid of O (N 2 ) at run time? If you eliminate objects for which collisions have already been checked, then you will reduce the execution time to O (N (N + 1) / 2), which is much faster, but still quite simple to implement (technically, it is still O (N 2 ) ). From a software development point of view, you can spend as a result more time than it costs to squeeze performance drops out of an improvement in a bad algorithm and an incorrectly chosen data structure. The cost-benefit ratio becomes increasingly disadvantageous and it is time to choose a more suitable data structure for handling collision recognition.

As a solution to the problem of collision recognition at runtime, space partitioning algorithms are actively used. They select a small part of the speed in advance, but logarithmically reduce the number of collision checks. The initial development time and CPU costs are easily outweighed by the benefits of scalability and increased speed.

Space partitioning concept


Let's take a step back and before moving on to the octodrees, consider the idea of ​​splitting the space and trees as a whole. If you do not understand this concept, then you will not be able to implement it in code.

In the implementation of a simple iteration above, we took each object in the game and compared its position with the positions of all the other objects to check if they were touching. All these objects are spatially located in the game world. If we create a shape that restricts the game world and find out which of the objects are contained in this shape, then we will have an area of ​​space with a list of objects contained in it. In our case, it will contain all the objects of the game.

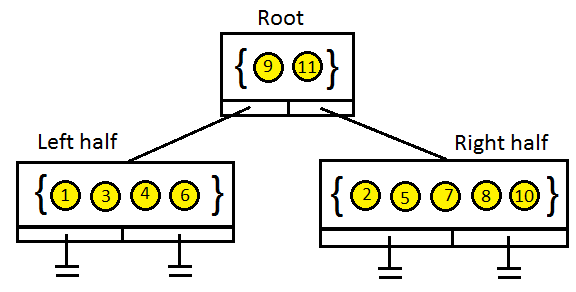
We can notice that one object is at one end of the world, and the other is at the opposite, so we don’t need to calculate collision checks between them in each frame. This will be a waste of precious processor time. Let's try to do something interesting! If we divide the world exactly in half, we can create three separate lists of objects.

The first list, List A, will contain all the objects on the left side of the world.

The second list, List B, contains objects from the right side of the world.

Some objects may touch the dividing line between the parts, that is, be on either side of it. For such objects, we will create a third list, List C.



It can be noted that with each division we spatially reduce the world in half and collect a list of objects in the resulting half. To store these lists, we can create a binary search tree. The concept of such a tree would look something like this:



The tree data structure in pseudocode looks like this:

 public class BinaryTree { //   ,      private List m_objectList; //         private BinaryTree m_left, m_right; //     (   ). private BinaryTree m_parent; }

We know that all objects in List A will never intersect with objects in List B, so almost half of the collision checks can be abandoned. We still have objects in List C that can touch objects in Lists A and B, so we will need to check all List C objects for collisions with all objects in Lists A, B and C.

If we continue to divide the world into smaller and smaller parts, then we will continue to reduce the number of checks, each time by half. This is the basic idea of ​​partitioning space. There are many ways to split the world into a tree-like data structure ( binary partitioning of space (BSP) , quadrant trees , K-dimensional trees , octree trees , etc.).

Now we will simply assume, by default, that the best division is division in half, exactly in the middle, because we believe that all objects are distributed around the world approximately evenly. This is a good assumption, but in some space partitioning algorithms perform a partition in such a way that in each of the halves there is an equal number of objects (weighted division), so that the resulting tree would be more balanced. However, what happens if all these objects start moving? To maintain a roughly equal split, you have to either move the section plane, or completely rebuild the tree in each frame. It is quite confusing and difficult.

Therefore, for my own implementation of the partitioning tree, I decided to divide it in half each time. As a result, some trees will be more sparse, but this is normal and will not lead to high costs.

Share or not to divide? That is the question.


Suppose we have a fairly sparse area with only a few objects. We can continue to perform the partition until we find the minimum possible bounding space for the last object. But is it necessary? Recall that the reason for creating a tree was the reduction in the number of collision checks performed in each frame, and not the creation of the region of space ideally restricting each object. Here are the rules I chose to decide whether to split or not:


You can take another step in halving and divide the two-dimensional space of the world into quadrants . The logic is essentially the same, but now we are checking for collisions between four squares, not two rectangles. We can continue the partitioning until the completion conditions are satisfied. The space of the world and the corresponding data structure for the quad tree will look something like this:



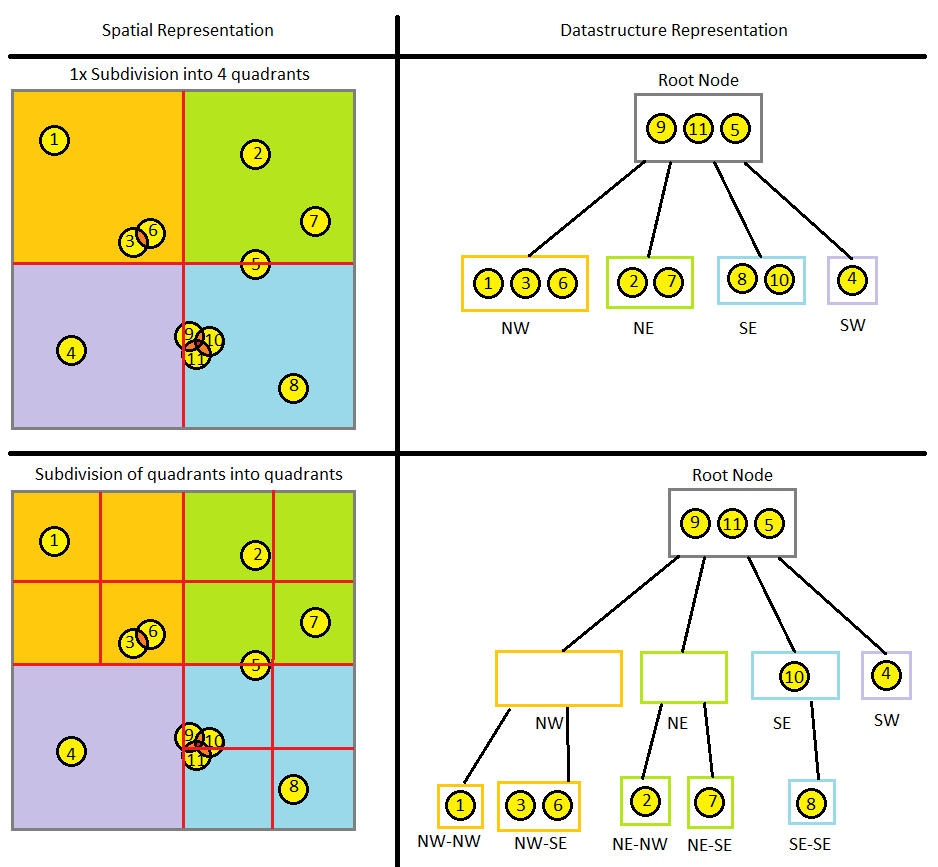
If the division into quad tree and data structure looks logical to you, then the octree will also be understandable. We simply add the third dimension and use bounding cubes, not squares, that is, we will have eight, not four possible children nodes. One may wonder what will happen if the game world has non-cubic dimensions, for example, 200x300x400. Anyway, you can use an octree with cubic dimensions — some child nodes will simply be empty if there is nothing in them in the space of the world. Obviously, it is necessary that the sizes of the octree are at least equal to the larger of the dimensions of the game world.

Creating oktotreev


So, as you have already read, octree is a special type of partitioning tree, usually used for objects in three-dimensional space (or anything with three dimensions). The bounding area will be a three-dimensional rectangle (parallelepiped) (usually a cube). Then we apply the logic described above and cut the bounding area into eight smaller parallelepipeds. If the game object is entirely placed in one of these subdivided areas, we drop it down the tree to the node of the area containing it. Then we continue to recursively divide each resulting area until one of the termination conditions is fulfilled. As a result, we should have a beautiful tree data structure.

In my implementation of an octree, there will be objects that have a bounding sphere and / or a bounding box. You will see that I use a large amount of code to determine which bounding shape is being used.

For the Octree class data structure, I chose the following rules for each tree:


Here is the outline code for my Octree class:

 public class OctTree { BoundingBox m_region; List m_objects; /// ///  ,       . ///        ,      .      . /// static Queue m_pendingInsertion = new Queue(); /// ///        . /// OctTree[] m_childNode = new OctTree[8]; /// ///   , ,     . ///    ,   ,        . /// byte m_activeNodes = 0; /// ///     -  1x1x1. /// const int MIN_SIZE = 1; /// ///  ,       . ,    .     ///     ,   ""     (64) /// int m_maxLifespan = 8; // int m_curLife = -1; //    ,     /// ///    .      . /// OctTree _parent; static bool m_treeReady = false; //     ,   ,      static bool m_treeBuilt = false; //      }

Initializing the bounding area


The first step in creating an octree is setting the bounding area of ​​the entire tree. This will be the bounding box for the root node of the tree, which initially contains all the objects in the game world. Before initializing the bounding volume, we need to make decisions regarding the design:

1. What should happen when an object moves beyond the bounding volume of the root node? Will we resize the entire tree so that all objects are limited? If so, then we will have to completely rebuild the octree from scratch. If not, then you need to find some way to process objects outside the boundaries, or to make sure that the objects never go beyond the boundaries.

2. How will we create the bounding area for the octree? Will we use predefined dimensions, for example, parallelepiped 200x400x200 (X, Y, Z)? Or we will use cubic sizes. being a power of two? What happens if the minimum acceptable bounding area cannot be divided? I decided that I would use a cubic bounding area with dimensions equal to a power of two, large enough to completely restrict the whole world. The minimum allowable area is a 1x1x1 cube. Thanks to this, I will clearly share the world and receive whole numbers (even though Vector3 has a floating-point format). I also decided that my bounding area would limit the whole world, so if an object leaves this area, it will be destroyed. For the minimum octant, I will perform a collision check by simple brute force. But I expect that no more than three objects at the same time will occupy such a small area, so O (N 2 ) performance costs are absolutely acceptable. I standardly initialize an octree with the help of a constructor that gets the size of the region and the list of objects inserted into the tree. It seemed to me that you should not show this part of the code, because it is elementary, but added it for completeness.

Here are my designers:

 /*:        ,        .*/ /// ///  ,         . /// ///   . ///  ,     private OctTree(BoundingBox region, List objList) { m_region = region; m_objects = objList; m_curLife = -1; } public OctTree() { m_objects = new List(); m_region = new BoundingBox(Vector3.Zero, Vector3.Zero); m_curLife = -1; } /// ///    ,     . /// ///    . /// :       ,     . public OctTree(BoundingBox region) { m_region = region; m_objects = new List(); m_curLife = -1; }

Create the initial octree


I'm a big fan of deferred initialization . I try to avoid allocating memory and doing work until it is absolutely necessary. In the case of an octree, I avoid creating a data structure for as long as possible. We receive a user request to insert an object into the data structure, but in fact we are not obliged to create a tree until someone starts a queue for it.

What does this give us? Well, suppose that the process of creating and traversing a tree will be quite resource intensive. If the user wants to give us 1000 objects for insertion into the tree, does it make sense to recalculate each subsequent bounding area a thousand times? ?

«» , . . , . , , . UpdateTree() . , , , .

 /// ///        . /// ///     ? private void UpdateTree() //    { if (!m_treeBuilt) { while (m_pendingInsertion.Count != 0) m_objects.Add(m_pendingInsertion.Dequeue()); BuildTree(); } else { while (m_pendingInsertion.Count != 0) Insert(m_pendingInsertion.Dequeue()); } m_treeReady = true; }

.

, . , , , , . , . , . , , , .

, . , , .

 /// ///     . /// private void BuildTree() //   { // ,       if (m_objects.Count <= 1) return; Vector3 dimensions = m_region.Max - m_region.Min; if (dimensions == Vector3.Zero) { FindEnclosingCube(); dimensions = m_region.Max - m_region.Min; } //,       if (dimensions.X <= MIN_SIZE && dimensions.Y <= MIN_SIZE && dimensions.Z <= MIN_SIZE) { return; } Vector3 half = dimensions / 2.0f; Vector3 center = m_region.Min + half; //      BoundingBox[] octant = new BoundingBox[8]; octant[0] = new BoundingBox(m_region.Min, center); octant[1] = new BoundingBox(new Vector3(center.X, m_region.Min.Y, m_region.Min.Z), new Vector3(m_region.Max.X, center.Y, center.Z)); octant[2] = new BoundingBox(new Vector3(center.X, m_region.Min.Y, center.Z), new Vector3(m_region.Max.X, center.Y, m_region.Max.Z)); octant[3] = new BoundingBox(new Vector3(m_region.Min.X, m_region.Min.Y, center.Z), new Vector3(center.X, center.Y, m_region.Max.Z)); octant[4] = new BoundingBox(new Vector3(m_region.Min.X, center.Y, m_region.Min.Z), new Vector3(center.X, m_region.Max.Y, center.Z)); octant[5] = new BoundingBox(new Vector3(center.X, center.Y, m_region.Min.Z), new Vector3(m_region.Max.X, m_region.Max.Y, center.Z)); octant[6] = new BoundingBox(center, m_region.Max); octant[7] = new BoundingBox(new Vector3(m_region.Min.X, center.Y, center.Z), new Vector3(center.X, m_region.Max.Y, m_region.Max.Z)); //     ,       . List[] octList = new List[8]; for (int i = 0; i < 8; i++) octList = new List(); //     ,    .       . List delist = new List(); foreach (Physical obj in m_objects) { if (obj.BoundingBox.Min != obj.BoundingBox.Max) { for (int a = 0; a < 8; a++) { if (octant[a].Contains(obj.BoundingBox) == ContainmentType.Contains) { octList[a].Add(obj); delist.Add(obj); break; } } } else if (obj.BoundingSphere.Radius != 0) { for (int a = 0; a < 8; a++) { if (octant[a].Contains(obj.BoundingSphere) == ContainmentType.Contains) { octList[a].Add(obj); delist.Add(obj); break; } } } } //        . foreach (Physical obj in delist) m_objects.Remove(obj); //  ,    ,     for (int a = 0; a < 8; a++) { if (octList[a].Count != 0) { m_childNode[a] = CreateNode(octant[a], octList[a]); m_activeNodes |= (byte)(1 << a); m_childNode[a].BuildTree(); } } m_treeBuilt = true; m_treeReady = true; } private OctTree CreateNode(BoundingBox region, List objList) //   { if (objList.Count == 0) return null; OctTree ret = new OctTree(region, objList); ret._parent = this; return ret; } private OctTree CreateNode(BoundingBox region, Physical Item) { List objList = new List(1); //         objList.Add(Item); OctTree ret = new OctTree(region, objList); ret._parent = this; return ret; }


, . - , , . , ?

1: , .

. , , . , , , , . , , « » :

  1. . . , .
  2. ́ , — .

2: , .

, . .

, , ? , . , , !

, . This is not true. , , , , . , . , , . .

, , , !

, . . , , , .

, , , ( - ). , . .

, , . , , . , , . , , .



, . . .

: ? , , ? , ?

, , . , , . , , , .

, . , , , . , - . , .

, .

, Update() . . , , ( ).

 public void Update(GameTime gameTime) { if (m_treeBuilt == true) { //        ,      . //   ,   .       ,    . //               if (m_objects.Count == 0) { if (HasChildren == false) { if (m_curLife == -1) m_curLife = m_maxLifespan; else if (m_curLife > 0) { m_curLife--; } } } else { if (m_curLife != -1) { if(m_maxLifespan <= 64) m_maxLifespan *= 2; m_curLife = -1; } } List movedObjects = new List(m_objects.Count); //         foreach (Physical gameObj in m_objects) { //  ,   ,        . if (gameObj.Update(gameTime)) { movedObjects.Add(gameObj); } } //     . int listSize = m_objects.Count; for (int a = 0; a < listSize; a++) { if (!m_objects[a].Alive) { if (movedObjects.Contains(m_objects[a])) movedObjects.Remove(m_objects[a]); m_objects.RemoveAt(a--); listSize--; } } //    . for( int flags = m_activeNodes, index = 0; flags > 0; flags >>=1, index++) if ((flags & 1) == 1) m_childNode[index].Update(gameTime); //  ,       ,        . //,       ,          . foreach (Physical movedObj in movedObjects) { OctTree current = this; //,       ,     //      //      ,      if (movedObj.BoundingBox.Max != movedObj.BoundingBox.Min) { while (current.m_region.Contains(movedObj.BoundingBox) != ContainmentType.Contains) if (current._parent != null) current = current._parent; else break; //  ,        } else { while (current.m_region.Contains(movedObj.BoundingSphere) != ContainmentType.Contains)//,     ,     . if (current._parent != null) current = current._parent; else break; } //           . m_objects.Remove(movedObj); current.Insert(movedObj); //        ,  . } //     for (int flags = m_activeNodes, index = 0; flags > 0; flags >>= 1, index++) if ((flags & 1) == 1 && m_childNode[index].m_curLife == 0) { m_childNode[index] = null; m_activeNodes ^= (byte)(1 << index); //       } //,          ,   . if (IsRoot == true) { //       . //               . //:  ,        . // 2:     ,    .         . List irList = GetIntersection(new List()); foreach (IntersectionRecord ir in irList) { if (ir.PhysicalObject != null) ir.PhysicalObject.HandleIntersection(ir); if (ir.OtherPhysicalObject != null) ir.OtherPhysicalObject.HandleIntersection(ir); } } } else { } }

Notice that for displaced objects we call the Insert () method . Inserting objects into a tree is very similar to the method used to create the original tree. Insert () tries to pull objects down through the tree as low as possible. I also strive to avoid creating new bounding spaces if one can use the existing ones in the child node.

 /// ///   ,       ,     /// ///   ///       private void Insert(T Item) where T : Physical { /*,     ,   -       ,   .*/ if (m_objects.Count <= 1 && m_activeNodes == 0) { m_objects.Add(Item); return; } Vector3 dimensions = m_region.Max - m_region.Min; //,       if (dimensions.X <= MIN_SIZE && dimensions.Y <= MIN_SIZE && dimensions.Z <= MIN_SIZE) { m_objects.Add(Item); return; } Vector3 half = dimensions / 2.0f; Vector3 center = m_region.Min + half; //           BoundingBox[] childOctant = new BoundingBox[8]; childOctant[0] = (m_childNode[0] != null) ? m_childNode[0].m_region : new BoundingBox(m_region.Min, center); childOctant[1] = (m_childNode[1] != null) ? m_childNode[1].m_region : new BoundingBox(new Vector3(center.X, m_region.Min.Y, m_region.Min.Z), new Vector3(m_region.Max.X, center.Y, center.Z)); childOctant[2] = (m_childNode[2] != null) ? m_childNode[2].m_region : new BoundingBox(new Vector3(center.X, m_region.Min.Y, center.Z), new Vector3(m_region.Max.X, center.Y, m_region.Max.Z)); childOctant[3] = (m_childNode[3] != null) ? m_childNode[3].m_region : new BoundingBox(new Vector3(m_region.Min.X, m_region.Min.Y, center.Z), new Vector3(center.X, center.Y, m_region.Max.Z)); childOctant[4] = (m_childNode[4] != null) ? m_childNode[4].m_region : new BoundingBox(new Vector3(m_region.Min.X, center.Y, m_region.Min.Z), new Vector3(center.X, m_region.Max.Y, center.Z)); childOctant[5] = (m_childNode[5] != null) ? m_childNode[5].m_region : new BoundingBox(new Vector3(center.X, center.Y, m_region.Min.Z), new Vector3(m_region.Max.X, m_region.Max.Y, center.Z)); childOctant[6] = (m_childNode[6] != null) ? m_childNode[6].m_region : new BoundingBox(center, m_region.Max); childOctant[7] = (m_childNode[7] != null) ? m_childNode[7].m_region : new BoundingBox(new Vector3(m_region.Min.X, center.Y, center.Z), new Vector3(center.X, m_region.Max.Y, m_region.Max.Z)); //-,        ? // 2:       .       ,     /. // .           .     . // :       256x256x256.    . if (Item.BoundingBox.Max != Item.BoundingBox.Min && m_region.Contains(Item.BoundingBox) == ContainmentType.Contains) { bool found = false; //     .       ,        . for(int a=0;a<8;a++) { //     ? if (childOctant[a].Contains(Item.BoundingBox) == ContainmentType.Contains) { if (m_childNode[a] != null) m_childNode[a].Insert(Item); //          ,     else { m_childNode[a] = CreateNode(childOctant[a], Item); //      m_activeNodes |= (byte)(1 << a); } found = true; } } if(!found) m_objects.Add(Item); } else if (Item.BoundingSphere.Radius != 0 && m_region.Contains(Item.BoundingSphere) == ContainmentType.Contains) { bool found = false; //     .       ,        . for (int a = 0; a < 8; a++) { //     ? if (childOctant[a].Contains(Item.BoundingSphere) == ContainmentType.Contains) { if (m_childNode[a] != null) m_childNode[a].Insert(Item); //A          ,     else { m_childNode[a] = CreateNode(childOctant[a], Item); //      m_activeNodes |= (byte)(1 << a); } found = true; } } if (!found) m_objects.Add(Item); } else { //      ,   .     ,    // ,      //BoundingBox enclosingArea = FindBox(); BuildTree(); } }

Collision detection


Finally, we built an octree tree and all the objects are where needed. How to perform collision detection? First, let's list the different ways in which we want to recognize collisions:

  1. . , . , . , .
  2. . , , , (, ). . , , .
  3. . , . «» (, ..).
  4. . , . , .

, / .

. , . , . . . .

, , . , , . - , . , (quad damage!), , .

, . , , .. , , .

:

 public class IntersectionRecord { Vector3 m_position; /// ///    3D-,    . /// public Vector3 Position { get { return m_position; } } Vector3 m_normal; /// ///       /// public Vector3 Normal { get { return m_normal; } } Ray m_ray; /// ///  ,    /// public Ray Ray { get { return m_ray; } } Physical m_intersectedObject1; /// ///  ,    /// public Physical PhysicalObject { get { return m_intersectedObject1; } set { m_intersectedObject1 = value; } } Physical m_intersectedObject2; /// ///     (   null, ,    -) /// public Physical OtherPhysicalObject { get { return m_intersectedObject2; } set { m_intersectedObject2 = value; } } /// ///       ,    .      ///           .   -       , ///        ,      . /// OctTree m_treeNode; /// ///       .      ,     . /// /// ,     /// ,   -      ,    . public override bool Equals(object otherRecord) { IntersectionRecord o = (IntersectionRecord)otherRecord; // // (m_intersectedObject1 != null && m_intersectedObject2 != null && m_intersectedObject1.ID == m_intersectedObject2.ID); if (otherRecord == null) return false; if (o.m_intersectedObject1.ID == m_intersectedObject1.ID && o.m_intersectedObject2.ID == m_intersectedObject2.ID) return true; if (o.m_intersectedObject1.ID == m_intersectedObject2.ID && o.m_intersectedObject2.ID == m_intersectedObject1.ID) return true; return false; } double m_distance; /// ///       . ///     ,      . /// public double Distance { get { return m_distance; } } private bool m_hasHit = false; public bool HasHit { get { return m_hasHit; } } public IntersectionRecord() { m_position = Vector3.Zero; m_normal = Vector3.Zero; m_ray = new Ray(); m_distance = float.MaxValue; m_intersectedObject1 = null; } public IntersectionRecord(Vector3 hitPos, Vector3 hitNormal, Ray ray, double distance) { m_position = hitPos; m_normal = hitNormal; m_ray = ray; m_distance = distance; // m_hitObject = hitGeom; m_hasHit = true; } /// ///    ,   ,   ,      . /// /// : ,    .   null. public IntersectionRecord(Physical hitObject = null) { m_hasHit = hitObject != null; m_intersectedObject1 = hitObject; m_position = Vector3.Zero; m_normal = Vector3.Zero; m_ray = new Ray(); m_distance = 0.0f; } } 


 /// ///     ,          /// ///      /  ///      private List GetIntersection(BoundingFrustum frustum, Physical.PhysicalType type = Physical.PhysicalType.ALL) { if (m_objects.Count == 0 && HasChildren == false) //   return null; List ret = new List(); //       foreach (Physical obj in m_objects) { //  ,     if ((int)((int)type & (int)obj.Type) == 0) continue; //   IntersectionRecord ir = obj.Intersects(frustum); if (ir != null) ret.Add(ir); } //       for (int a = 0; a < 8; a++) { if (m_childNode[a] != null && (frustum.Contains(m_childNode[a].m_region) == ContainmentType.Intersects || frustum.Contains(m_childNode[a].m_region) == ContainmentType.Contains)) { List hitList = m_childNode[a].GetIntersection(frustum); if (hitList != null) { foreach (IntersectionRecord ir in hitList) ret.Add(ir); } } } return ret; }

, . , , . , :

 /// ///         /// /// public int Render() { int triangles = 0; //    ,       //       foreach (IntersectionRecord ir in m_octTree.AllIntersections(m_cameras[m_activeCamera].Frustum)) { ir.PhysicalObject.SetDirectionalLight(m_globalLight[0].Direction, m_globalLight[0].Color); ir.PhysicalObject.View = m_cameras[m_activeCamera].View; ir.PhysicalObject.Projection = m_cameras[m_activeCamera].Projection; ir.PhysicalObject.UpdateLOD(m_cameras[m_activeCamera]); triangles += ir.PhysicalObject.Render(m_cameras[m_activeCamera]); } return triangles; } 


 /// ///       ,     /// /// ,     ///    private List GetIntersection(Ray intersectRay, Physical.PhysicalType type = Physical.PhysicalType.ALL) { if (m_objects.Count == 0 && HasChildren == false) //   return null; List ret = new List(); //    ,              . //        foreach (Physical obj in m_objects) { //   ,     if ((int)((int)type & (int)obj.Type) == 0) continue; if (obj.BoundingBox.Intersects(intersectRay) != null) { IntersectionRecord ir = obj.Intersects(intersectRay); if (ir.HasHit) ret.Add(ir); } } //       for (int a = 0; a < 8; a++) { if (m_childNode[a] != null && m_childNode[a].m_region.Intersects(intersectRay) != null) { List hits = m_childNode[a].GetIntersection(intersectRay, type); if (hits != null) { foreach (IntersectionRecord ir in hits) ret.Add(ir); } } } return ret; }


( . Update() ). , .

. . . , . , , . . , , , .





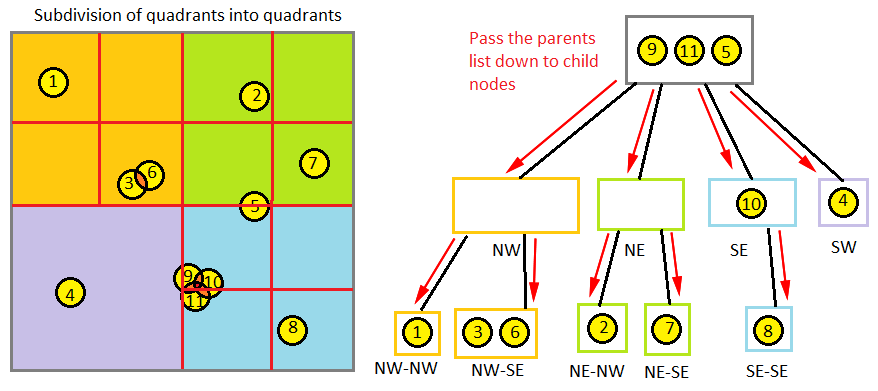
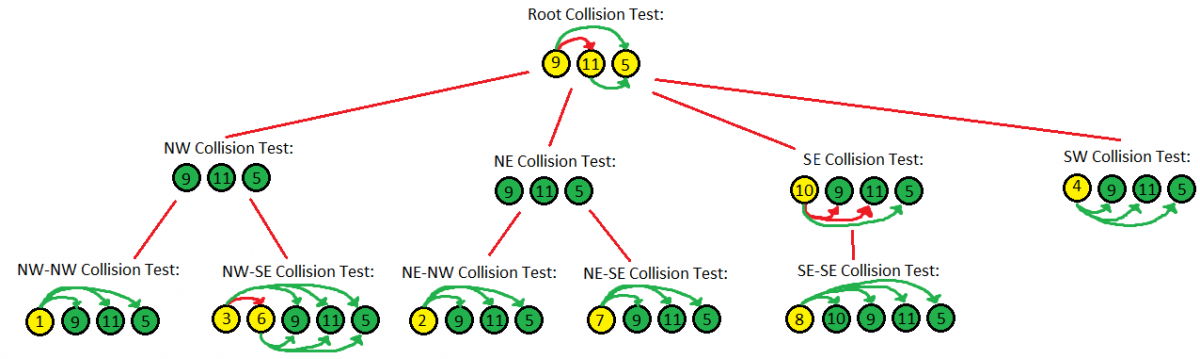
, , 29 4. , [11*11 = 121] .

 private List GetIntersection(List parentObjs, Physical.PhysicalType type = Physical.PhysicalType.ALL) { List intersections = new List(); // ,          . //            foreach (Physical pObj in parentObjs) { foreach (Physical lObj in m_objects) { //    .   ,      . //   ,   . IntersectionRecord ir = pObj.Intersects(lObj); if (ir != null) { intersections.Add(ir); } } } //         if (m_objects.Count > 1) { #region self-congratulation /* *     .      foreach,  : * foreach(Physical lObj1 in m_objects) * { * foreach(Physical lObj2 in m_objects) * { * //    * } * } * *   ,    O(N*N)    ,      . * ,        : {1,2,3,4} *    {1}  {1,2,3,4} *   {2}  {1,2,3,4}, *     {1}  {2},    {2}  {1}    .     ,  {1}? *     4+3+2+1  ,    O(N(N+1)/2).  N = 10,       . *           for,       foreach,    *  for(int i=0;i tmp = new List(m_objects.Count); tmp.AddRange(m_objects); while (tmp.Count > 0) { foreach (Physical lObj2 in tmp) { if (tmp[tmp.Count - 1] == lObj2 || (tmp[tmp.Count - 1].IsStatic && lObj2.IsStatic)) continue; IntersectionRecord ir = tmp[tmp.Count - 1].Intersects(lObj2); if (ir != null) intersections.Add(ir); } //      ,    O(N(N+1)/2)   O(N*N) tmp.RemoveAt(tmp.Count-1); } } //         ,        . foreach (Physical lObj in m_objects) if (lObj.IsStatic == false) parentObjs.Add(lObj); //parentObjs.AddRange(m_objects); //       ,        . for (int flags = m_activeNodes, index = 0; flags > 0; flags >>= 1, index++) if ((flags & 1) == 1) intersections.AddRange(m_childNode[index].GetIntersection(parentObjs, type)); return intersections; } ;i++)>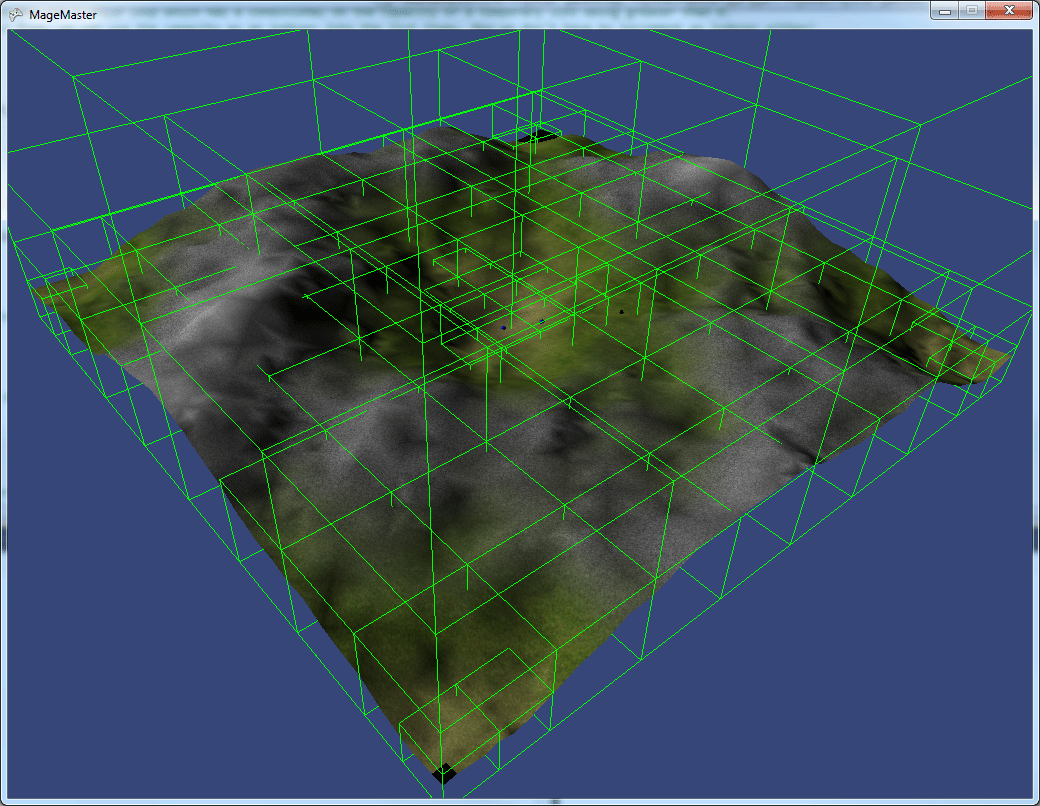



, .


, . , .

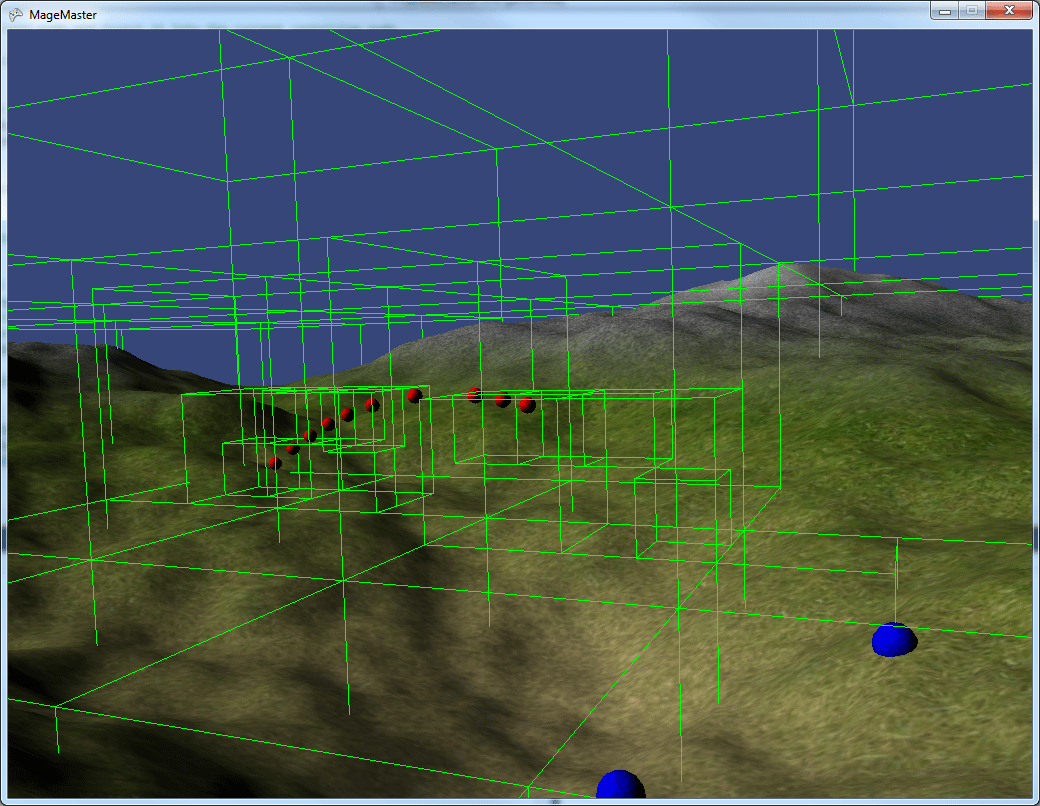
Source: https://habr.com/ru/post/334990/

More articles:


All Articles