Advanced tactics of the game "Minesweeper"
[Friday's translation of the 1999 article by one of the authors of the Thief Sean Barrett game engine]
In this position, I know that there are a lot of mines around me, but I cannot determine where they are. A few mines can be in one of two places (pink or blue), a group of mines can be located in one of two combinations (light / dark green). In addition, there is still a difficult situation with "5" and "6" in the upper left corner, which I did not single out.

Blue / pink - mutually exclusive pairs, light / dark green - mutually exclusive groups
')
In the "Minesweeper" can be played in two ways: as in a logical or in a probability game.
Technically, probability implies logic. If you can logically prove that the mine should be in a certain place, then the probability is 100%. If you can prove that it is not in this place, then the probability is 0%. That is, in a sense, only probabilities are important to us. However, the player uses logical deduction to recognize such 100% situations. Sometimes, especially at low levels of complexity, it is enough to pass a level, no calculation of probabilities is required.
But there are situations where the entire logic of the world cannot save you. A simple example is the “T” situation, which is seen down the center. It is slightly complicated by additional adjacent mines. (In the simplest case, “2” is replaced by “1”, and “5” is replaced by “3” so that the situation is symmetrical.)
There is no way to get more information about the probable position of one mine left in one of these cells. Chances are fifty to fifty - you can throw a coin. When you get something like this, it is better to immediately make a choice and do not put it off until later. If the guess is incorrect, then you at least save time on resolving the rest of the field. (But personally, I strive for completeness, so I leave such cases for later. And don’t blame yourself for not guessing. When winning or losing depends on a coin toss, this is a bad game design.)
In the endgame, you can use a very simple tactic - count the number of remaining mines. Suppose I decided everything except the bottom right of the field. There may be only two configurations of mines corresponding to the data:

Possible configurations of mines in the lower right corner
If you get such a position and the counter says that there are only two mines left, then the answer is ready: it should be configuration B.
If the meter says that there are three mines left, then this is not necessarily A configuration. This may be scheme B with a remaining mine in one of the right bottom groups of 3x3 cells.
In fact, the odds are in favor of configuration b .
If you explore probabilities only “locally,” you can see that each of the cells in the marked mutually exclusive groups has a 50-50 chance of being a mine. Saying “locally”, I mean that if next to two unknown cells is “1”, then the probability of a hidden mine is 50% for each of them.
This is exactly the situation at the bottom in the center: each of the neighboring cells adjacent to an unknown pair contains exactly one mine, that is, each of the adjacent data fragments suggests a 50 percent probability. In the upper left corner is a similar situation:
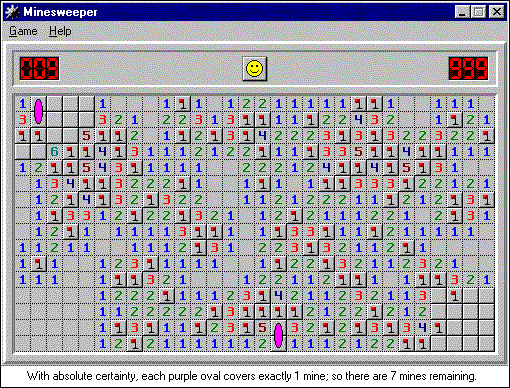
With absolute accuracy in each of the pink ovals there is one mine, that is only 7 minutes left
The situation in the lower right corner is also somewhat similar: next to each of the numbers on the “border” there is one mine and two cells in which it can be.
If there is one hidden mine next to the cell, but three closed cells, then the probability of a mine in each of the cells is 33%; each of the four closed cells has a probability of 25%. If we have two hidden mines and three closed cells, then each cell has a probability of 66%.
Here is the situation with "local probability" for the entire field:
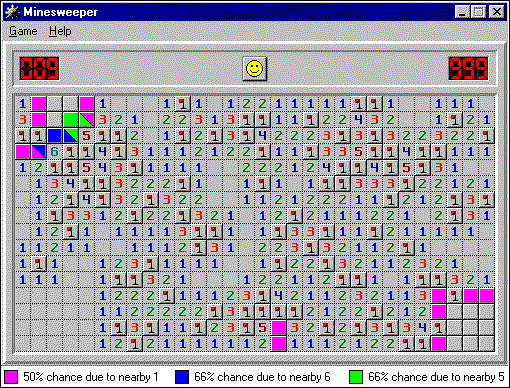
As you can see, several cells in the upper left area have several probabilities; closed cell next to "2" and "6" and one next to "3" and "5". (Thanks to them, the cell next to “5” and “6” still has a probability of 66%, so there is no visible discrepancy.)
You probably wonder what the presence of conflicting local probabilities means. Intuition may suggest that the greatest probability should win. For example, a cell between “6” and “2” should actually have 66%. This will mean that in the extreme left cell with a probability of 50%, it is actually equal to 33%. Or you can try to somehow combine priorities: perhaps the probability will be 5/6 or the average.
But none of this is really wrong. The data from which the probabilities are derived is not independent of each other, so no straightforward mathematical calculations will be true. The reason for the correctness of the local guess about 50% down in the center is that it is really independent of anything else. If we randomly recreate the field according to the data we already have, then exactly half of the mine models will be in one of two cells. (Probability sometimes confuses people who cannot figure out which rules for calculating probabilities apply in a particular situation. This approach is guaranteed the right way because it is based on determining probabilities in statistical prediction: the calculation is performed by measuring in all possible configurations that could lead to the current situation, with all of them considered equally likely.)
That is, for correct measurements in the situation in the upper left corner, you need to consider all possible mine configurations that satisfy the data already collected, and then calculate what percentage of them contain a mine in the desired position.
Direct counting would be time consuming. Fortunately, there are other ways.
An abstract method for calculating probabilities consists in traversing all possible mine configurations, discarding configurations that do not match the collected data, and calculating statistics for each of the possible positions.
A more practical approach is to consider only those options that cannot be discarded. To do this, we need to apply logic and generate all possible situations that may correspond to the available data. I have already shown two options for the lower right corner, but the probabilities for the upper left:
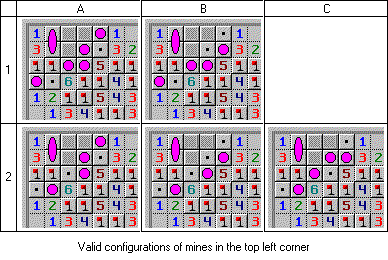
Possible configurations for the upper left corner
(As before, the oval with a height of two cells shows that the mine can with equal probability be located in any of the cells. I could enumerate each of these two cases separately, that is, we would have 10 configurations, but there is no use for us The structure of the table: two rows (numbered as "1" and "2") differ in the position of the mines in the fourth row. Three columns are characterized by the position of mines in the second row.)
Now there is a temptation to exclaim: “Aha, here are five cases, so that we can calculate the number of cases for each of the possible mine positions.” For example, the mine is in the fourth row (near the lower left “1”) is on the left in the upper two cases, and in the right in the three lower cases. Therefore, we can decide that it has a probability of 60% to be on the right, next to "6." (This is a position with conflicting local probabilities of 50% and 66%.)
However, we miss one subtlety - the number of mines in some cases is different: A1 has six minutes, B2 has four, and five each in all other cases.
For a detailed study of this subtlety, let's return to a simpler situation in the lower right corner.

Possible configurations with lower right
Suppose I have already discovered the rest of the field, and I know that there are exactly three mines left.
It is tempting to assume that the most likely configuration is A with exactly three mines. But this is not true.
Another temptation is to remember how many were mines and how many total cells, and say: “What are the chances that the lower 3x3 area will be empty?” This is also not true. It is very difficult to explain why this is a mistake, probably, it can be compared with the Monty Hall paradox . However, suffice it to say that in reality the chances in this situation do not depend on the total number of mines and the size of the field.
The correct answer is: how many possible configurations of the three minutes correspond to our knowledge of the field? From the figure we see that two: configurations A and B. But in B there are only two mines. The third mine can be in any of the cells of the lower 3x3 area, about which we have not yet collected any data. That is, there are nine variants of B configurations, I just did not depict them all.
Therefore, there are only ten possible configurations. Each of the ten configurations is equally likely. (As I mentioned earlier, this is critically important to understand the likelihood. The chances that the computer generated any of these options are small, but they are equally small, because the computer [as far as we know] gave each configuration equal chances. You can throw away a configuration of ten "eagles" in a row and a sequence of two "eagles", one "tails", one "eagle", three "tails", one "eagle", one "tails" and one "eagle" . More likely to throw out a total of five " Eagles "and five" heads, but not any specific sequence of "eagles" and " reshek ". In the" Sapyor "we are dealing with mine configurations that are similar to the sequence of coin flips.)
Since each of the ten configurations (nine for B , one for A ) is equally probable, configuration B in this case has a probability of 90%!
If there were four mines at this stage, then configuration A would have nine options. Configuration B would have one option for each of the two minutes in the lower left corner; this is C (9.2) , that is, 9! / ((9-2)! * 2!) or 9 * 8/2, equal to 36. In this case, configuration B would have only 75% probability.
With five mines, configuration A would have 36 options, and configuration B would have 9 * 8 * 7/6 = 84 options; that is, the chances of B would be slightly more than 66%.
In the case of six minutes, B would have a probability of 60%. With seven mines, B would have only 50%. With eight mines, B would be less likely than A; in this case, with so many mines in the remaining positions of the configurations it becomes smaller. Consider the worst case when 11 minutes left. (The chance of this is extremely small, but if such a situation arises, then these probabilities are applicable.) In configuration B , in all closed cells there will be mines, in configuration A in all but one. That is, there are 9 options for A and only one for B.
On the field we have, there are nine minutes left. One of them is located in the central lower area, and its position is completely independent, so you can ignore it. That is, we consider the entire field, except for this case: only eight minutes have not been found. (To avoid confusion, I will continue to explicitly count the oval in the upper left corner, because this is an image of the upper left corner.)
Any combination of the top left and bottom right configurations can be added, except for one of them (A1 + A), which requires nine minutes. Therefore, we must list each of these possible configurations and count the remaining mines and closed cells.
In fact, the number of closed cells is independent: there are nine in the lower right corner and three in the upper left, that is, a total of 12.
Thus, there are 118 possible combinations. Based on this, we can independently calculate the number of combinations for each of the left upper and right lower configurations:
Then I went around each cell on the field and calculated its probability, summing up the number of probabilities in which it appears, and dividing by 118. (Actually, simply adding the percentages mentioned above.) In addition, on average, in each of the closed cells there is a mine 15 out of 118 options (that is, the chances that there is a mine in at least one closed cell are very high). [This can be calculated by multiplying the number of remaining mines by closed variants, which gives us the average number of mines in closed cells.]

Mines probabilities
(It should be said that this does not show all available information. For example, we know that the probabilities of two dark green cells are 87% related - if one is correct, then the other too. And blue 13% cells that have mines by configuration A , too, are connected. The remaining blue 13% cells are not connected. If one of them contains a mine, the probability that there is a mine in any of the remaining ones decreases.)
Most likely, playing in the "Minesweeper", you do not want to hang on all these calculations.
And me too.
But I did list all possible configurations in the upper left and lower right corners. I noticed that in one configuration ( B2-B ) it is used one mine less than in all the others, and applied the time-tested rule “less min - means more closed variants” (which is valid until the number of closed cells is less than twice the number missing min). This means that configurations with fewer mines are much more likely.
Since there were many configurations in the upper left corner, determining the odds for any cell is rather difficult. So I just found out that configuration B in the lower right corner is much more likely, and I accidentally chose one of the suitable cells. (I hoped that it would allow me to finish the lower right corner, and then, armed with more information about the number of remaining mines, I could complete the upper left corner, after which I would have to throw a coin to select below in the center. Of course, ideally, I had to choose a cell maximizing the likelihood of obtaining useful information, but any of these guesses would allow me to “enter” into the lower right corner for further data collection.) The odds were higher for configuration B , so I chose the cell in which mine was in configuration A.

Eight times out of nine I would be right.
Unpleasant situation in the "Saper"
In this position, I know that there are a lot of mines around me, but I cannot determine where they are. A few mines can be in one of two places (pink or blue), a group of mines can be located in one of two combinations (light / dark green). In addition, there is still a difficult situation with "5" and "6" in the upper left corner, which I did not single out.

Blue / pink - mutually exclusive pairs, light / dark green - mutually exclusive groups
')
Minesweeper: Logic or Probability
In the "Minesweeper" can be played in two ways: as in a logical or in a probability game.
Technically, probability implies logic. If you can logically prove that the mine should be in a certain place, then the probability is 100%. If you can prove that it is not in this place, then the probability is 0%. That is, in a sense, only probabilities are important to us. However, the player uses logical deduction to recognize such 100% situations. Sometimes, especially at low levels of complexity, it is enough to pass a level, no calculation of probabilities is required.
But there are situations where the entire logic of the world cannot save you. A simple example is the “T” situation, which is seen down the center. It is slightly complicated by additional adjacent mines. (In the simplest case, “2” is replaced by “1”, and “5” is replaced by “3” so that the situation is symmetrical.)
There is no way to get more information about the probable position of one mine left in one of these cells. Chances are fifty to fifty - you can throw a coin. When you get something like this, it is better to immediately make a choice and do not put it off until later. If the guess is incorrect, then you at least save time on resolving the rest of the field. (But personally, I strive for completeness, so I leave such cases for later. And don’t blame yourself for not guessing. When winning or losing depends on a coin toss, this is a bad game design.)
Tactics at the end of the game
In the endgame, you can use a very simple tactic - count the number of remaining mines. Suppose I decided everything except the bottom right of the field. There may be only two configurations of mines corresponding to the data:

Possible configurations of mines in the lower right corner
If you get such a position and the counter says that there are only two mines left, then the answer is ready: it should be configuration B.
If the meter says that there are three mines left, then this is not necessarily A configuration. This may be scheme B with a remaining mine in one of the right bottom groups of 3x3 cells.
In fact, the odds are in favor of configuration b .
Local probabilities
If you explore probabilities only “locally,” you can see that each of the cells in the marked mutually exclusive groups has a 50-50 chance of being a mine. Saying “locally”, I mean that if next to two unknown cells is “1”, then the probability of a hidden mine is 50% for each of them.
This is exactly the situation at the bottom in the center: each of the neighboring cells adjacent to an unknown pair contains exactly one mine, that is, each of the adjacent data fragments suggests a 50 percent probability. In the upper left corner is a similar situation:

With absolute accuracy in each of the pink ovals there is one mine, that is only 7 minutes left
The situation in the lower right corner is also somewhat similar: next to each of the numbers on the “border” there is one mine and two cells in which it can be.
If there is one hidden mine next to the cell, but three closed cells, then the probability of a mine in each of the cells is 33%; each of the four closed cells has a probability of 25%. If we have two hidden mines and three closed cells, then each cell has a probability of 66%.
Here is the situation with "local probability" for the entire field:

As you can see, several cells in the upper left area have several probabilities; closed cell next to "2" and "6" and one next to "3" and "5". (Thanks to them, the cell next to “5” and “6” still has a probability of 66%, so there is no visible discrepancy.)
Local Conflict Resolution
You probably wonder what the presence of conflicting local probabilities means. Intuition may suggest that the greatest probability should win. For example, a cell between “6” and “2” should actually have 66%. This will mean that in the extreme left cell with a probability of 50%, it is actually equal to 33%. Or you can try to somehow combine priorities: perhaps the probability will be 5/6 or the average.
But none of this is really wrong. The data from which the probabilities are derived is not independent of each other, so no straightforward mathematical calculations will be true. The reason for the correctness of the local guess about 50% down in the center is that it is really independent of anything else. If we randomly recreate the field according to the data we already have, then exactly half of the mine models will be in one of two cells. (Probability sometimes confuses people who cannot figure out which rules for calculating probabilities apply in a particular situation. This approach is guaranteed the right way because it is based on determining probabilities in statistical prediction: the calculation is performed by measuring in all possible configurations that could lead to the current situation, with all of them considered equally likely.)
That is, for correct measurements in the situation in the upper left corner, you need to consider all possible mine configurations that satisfy the data already collected, and then calculate what percentage of them contain a mine in the desired position.
Direct counting would be time consuming. Fortunately, there are other ways.
Counting configurations
An abstract method for calculating probabilities consists in traversing all possible mine configurations, discarding configurations that do not match the collected data, and calculating statistics for each of the possible positions.
A more practical approach is to consider only those options that cannot be discarded. To do this, we need to apply logic and generate all possible situations that may correspond to the available data. I have already shown two options for the lower right corner, but the probabilities for the upper left:

Possible configurations for the upper left corner
(As before, the oval with a height of two cells shows that the mine can with equal probability be located in any of the cells. I could enumerate each of these two cases separately, that is, we would have 10 configurations, but there is no use for us The structure of the table: two rows (numbered as "1" and "2") differ in the position of the mines in the fourth row. Three columns are characterized by the position of mines in the second row.)
Now there is a temptation to exclaim: “Aha, here are five cases, so that we can calculate the number of cases for each of the possible mine positions.” For example, the mine is in the fourth row (near the lower left “1”) is on the left in the upper two cases, and in the right in the three lower cases. Therefore, we can decide that it has a probability of 60% to be on the right, next to "6." (This is a position with conflicting local probabilities of 50% and 66%.)
However, we miss one subtlety - the number of mines in some cases is different: A1 has six minutes, B2 has four, and five each in all other cases.
We consider mines not found
For a detailed study of this subtlety, let's return to a simpler situation in the lower right corner.

Possible configurations with lower right
Suppose I have already discovered the rest of the field, and I know that there are exactly three mines left.
It is tempting to assume that the most likely configuration is A with exactly three mines. But this is not true.
Another temptation is to remember how many were mines and how many total cells, and say: “What are the chances that the lower 3x3 area will be empty?” This is also not true. It is very difficult to explain why this is a mistake, probably, it can be compared with the Monty Hall paradox . However, suffice it to say that in reality the chances in this situation do not depend on the total number of mines and the size of the field.
The correct answer is: how many possible configurations of the three minutes correspond to our knowledge of the field? From the figure we see that two: configurations A and B. But in B there are only two mines. The third mine can be in any of the cells of the lower 3x3 area, about which we have not yet collected any data. That is, there are nine variants of B configurations, I just did not depict them all.
Therefore, there are only ten possible configurations. Each of the ten configurations is equally likely. (As I mentioned earlier, this is critically important to understand the likelihood. The chances that the computer generated any of these options are small, but they are equally small, because the computer [as far as we know] gave each configuration equal chances. You can throw away a configuration of ten "eagles" in a row and a sequence of two "eagles", one "tails", one "eagle", three "tails", one "eagle", one "tails" and one "eagle" . More likely to throw out a total of five " Eagles "and five" heads, but not any specific sequence of "eagles" and " reshek ". In the" Sapyor "we are dealing with mine configurations that are similar to the sequence of coin flips.)
Since each of the ten configurations (nine for B , one for A ) is equally probable, configuration B in this case has a probability of 90%!
If there were four mines at this stage, then configuration A would have nine options. Configuration B would have one option for each of the two minutes in the lower left corner; this is C (9.2) , that is, 9! / ((9-2)! * 2!) or 9 * 8/2, equal to 36. In this case, configuration B would have only 75% probability.
With five mines, configuration A would have 36 options, and configuration B would have 9 * 8 * 7/6 = 84 options; that is, the chances of B would be slightly more than 66%.
In the case of six minutes, B would have a probability of 60%. With seven mines, B would have only 50%. With eight mines, B would be less likely than A; in this case, with so many mines in the remaining positions of the configurations it becomes smaller. Consider the worst case when 11 minutes left. (The chance of this is extremely small, but if such a situation arises, then these probabilities are applicable.) In configuration B , in all closed cells there will be mines, in configuration A in all but one. That is, there are 9 options for A and only one for B.
Final decision
On the field we have, there are nine minutes left. One of them is located in the central lower area, and its position is completely independent, so you can ignore it. That is, we consider the entire field, except for this case: only eight minutes have not been found. (To avoid confusion, I will continue to explicitly count the oval in the upper left corner, because this is an image of the upper left corner.)
Any combination of the top left and bottom right configurations can be added, except for one of them (A1 + A), which requires nine minutes. Therefore, we must list each of these possible configurations and count the remaining mines and closed cells.
In fact, the number of closed cells is independent: there are nine in the lower right corner and three in the upper left, that is, a total of 12.
| Top left | Bottom right | Min | Min left | Closed options |
|---|---|---|---|---|
| A1 | B | eight | 0 | one |
| B1 | A | eight | 0 | one |
| B1 | B | 7 | one | 12 |
| A2 | A | eight | 0 | one |
| A2 | B | 7 | one | 12 |
| B2 | A | 7 | one | 12 |
| B2 | B | 6 | 2 | 66 |
| C2 | A | eight | 0 | one |
| C2 | B | 7 | one | 12 |
Thus, there are 118 possible combinations. Based on this, we can independently calculate the number of combinations for each of the left upper and right lower configurations:
| Configuration | Options | Percent |
|---|---|---|
| A1 | one | one |
| B1 | 13 | eleven |
| A2 | 13 | eleven |
| B2 | 78 | 66 |
| C2 | 13 | eleven |
| A | 15 | 13 |
| B | 103 | 87 |
Then I went around each cell on the field and calculated its probability, summing up the number of probabilities in which it appears, and dividing by 118. (Actually, simply adding the percentages mentioned above.) In addition, on average, in each of the closed cells there is a mine 15 out of 118 options (that is, the chances that there is a mine in at least one closed cell are very high). [This can be calculated by multiplying the number of remaining mines by closed variants, which gives us the average number of mines in closed cells.]

Mines probabilities
(It should be said that this does not show all available information. For example, we know that the probabilities of two dark green cells are 87% related - if one is correct, then the other too. And blue 13% cells that have mines by configuration A , too, are connected. The remaining blue 13% cells are not connected. If one of them contains a mine, the probability that there is a mine in any of the remaining ones decreases.)
Playing a game
Most likely, playing in the "Minesweeper", you do not want to hang on all these calculations.
And me too.
But I did list all possible configurations in the upper left and lower right corners. I noticed that in one configuration ( B2-B ) it is used one mine less than in all the others, and applied the time-tested rule “less min - means more closed variants” (which is valid until the number of closed cells is less than twice the number missing min). This means that configurations with fewer mines are much more likely.
Since there were many configurations in the upper left corner, determining the odds for any cell is rather difficult. So I just found out that configuration B in the lower right corner is much more likely, and I accidentally chose one of the suitable cells. (I hoped that it would allow me to finish the lower right corner, and then, armed with more information about the number of remaining mines, I could complete the upper left corner, after which I would have to throw a coin to select below in the center. Of course, ideally, I had to choose a cell maximizing the likelihood of obtaining useful information, but any of these guesses would allow me to “enter” into the lower right corner for further data collection.) The odds were higher for configuration B , so I chose the cell in which mine was in configuration A.

Eight times out of nine I would be right.
Source: https://habr.com/ru/post/334216/
All Articles