Geekly Articles each Day
📜 ⬆️ ⬇️

PostgreSQL Indexes - 5


Last time we looked at the PostgreSQL indexing mechanism , the interface of access methods , and two methods: a hash index and a B-tree . In this part of the deal indices GiST.

GiST


GiST is short for generalized search tree. This is a balanced search tree, just like the previously considered b-tree.

What is the difference? The b-tree index is rigidly tied to the semantics of the comparison: the support of the operators “more”, “less”, “equal” is all that it is capable of (but it is capable of very well!). But modern databases also store data types for which these operators simply do not make sense: geodata, text documents, pictures ...
')
This is where the GiST index method comes in. It allows you to specify the principle of the distribution of data of any type on a balanced tree, and the method of using this view for access by some operator. For example, an R-tree for spatial data with support for relative position operators (located on the left, right; contains, etc.) or an RD tree for sets with support for intersection or entry operators can be “laid down” in the GiST index.

Due to the extensibility in PostgreSQL, it is quite possible to create a completely new access method from scratch: to do this, you need to implement an interface with an indexing mechanism. But this requires thinking through not only the indexing logic, but also the page structure, effective implementation of locks, support of the proactive write log - which implies a very high qualification of the developer and greater complexity. GiST simplifies the task by taking on low-level problems and providing its own interface: several functions related not to the technical field, but to the application area. In this sense, we can say that GiST is a framework for building new access methods.

Device


GiST is a height-balanced tree consisting of page nodes. Nodes consist of index entries.

Each record of a leaf node (leaf record) contains, in the most general form, a certain predicate (a logical expression) and a link to a table row (TID). Indexed data (key) must satisfy this predicate.

Each internal node record (internal record) also contains a predicate and a link to the child node, all indexed data of the child subtree must satisfy this predicate. In other words, the predicate of the inner record includes the predicates of all the child records. This is an important property that replaces the GiST index with a simple ordering of the B-tree.

The search in the GiST tree uses the special consistent function (consistent) - one of the functions defined by the interface, and implemented in its own way for each supported operator family.

The consistency function is called for the index record and determines whether the predicate of this record is “consistent” with the search condition (of the form “ indexed-field operator expression ”). For the internal record, it actually determines whether it is necessary to go down to the appropriate subtree, and for the sheet record, whether the indexed data satisfies the condition.

The search, as usual in the tree, begins with the root node. With the help of the consistency function, it becomes clear which subsidiaries it makes sense to enter (there may be several of them), and which ones - not. Then the algorithm is repeated for each of the found child nodes. If the node is a leaf, then the record selected by the consistency function is returned as one of the results.

The search is performed in depth: the algorithm first tries to get to some leaf node. This allows you to quickly return the first results (which may be important if the user is not interested in all the results, but only a few).

Note once again that the consistency function should not have anything to do with the “more”, “less” or “equal” operators. Its semantics may be completely different, and therefore it is not intended that the index will produce values ​​in any particular order.

We will not consider the algorithms for inserting and deleting values ​​in GiST - for this we use several more interface functions . But there is one important point. When a new value is inserted into the index for it, such a parent record is selected so that its predicate should be expanded as little as possible (ideally, not expanded at all). But when the value is deleted, the predicate of the parent record is no longer narrowed. This happens only in two cases: when a page is divided into two (when there is not enough space on the page to insert a new index record) and when the index is completely rebuilt (using the reindex or vacuum full commands). Therefore, the effectiveness of the GiST index with frequently changing data may degrade over time.

Next we look at a few examples of indexes for different data types and the useful properties of GiST:


R-tree for points


Let us demonstrate the above with the example of an index for points on a plane (similar indices can be constructed for other geometric objects). A regular B-tree is not suitable for this data type, since comparison points are not defined for points.

The idea of ​​an R-tree is that the plane is divided into rectangles, which together cover all indexed points. The index record stores a rectangle, and the predicate can be formulated as follows: “the desired point lies inside this rectangle”.

The root of the R-tree will contain some of the largest rectangles (perhaps even intersecting). Child nodes will contain smaller rectangles nested in the parent, collectively covering all the underlying points.

Sheet nodes, in theory, should contain indexed points, but the data type in all index records must match; therefore, all the same rectangles are stored, but “collapsed” to dots.

To visualize such a structure visually, below are the drawings of the three levels of the R-tree; The points represent the coordinates of airports (similar to the airports table of the demo database, but more data is taken from the openflights.org site).


First level; two large intersecting rectangles are visible.


Second level; large rectangles are divided into smaller areas.


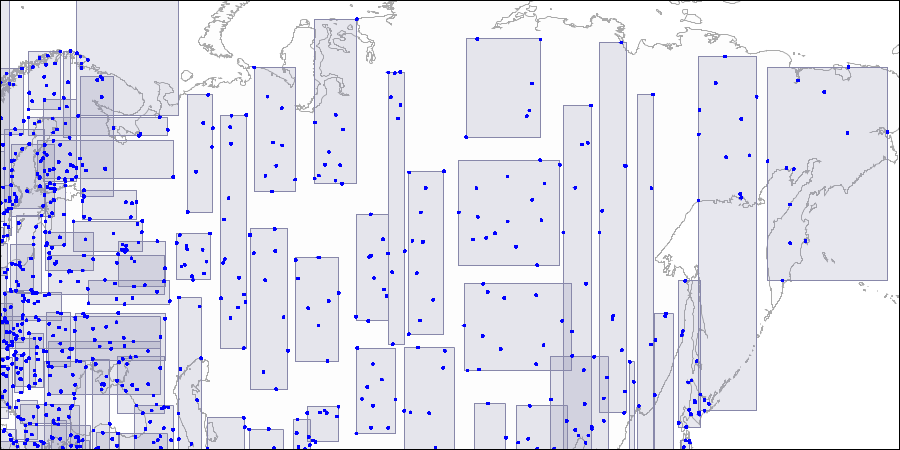
Third level; each rectangle contains so many points to fit on one index page.

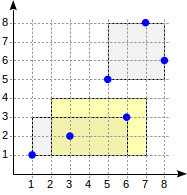
Now let's take a closer look at a very simple “one-level” example:



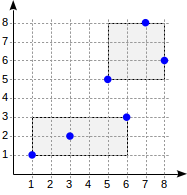
postgres=# create table points(p point);
CREATE TABLE
postgres=# insert into points(p) values
(point '(1,1)'), (point '(3,2)'), (point '(6,3)'),
(point '(5,5)'), (point '(7,8)'), (point '(8,6)');
INSERT 0 6
postgres=# create index on points using gist(p);
CREATE INDEX

The index structure for such a partition will look like this:



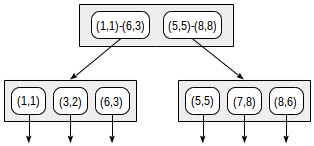
The created index can be used to speed up, for example, the following query: “find all points included in a given rectangle”. This condition is formulated as follows: p <@ box '(2,1),(6,3)' (operator <@ from the points_ops family means “contained in”):

postgres=# set enable_seqscan = off;
SET
postgres=# explain(costs off) select * from points where p <@ box '(2,1),(7,4)';
QUERY PLAN
----------------------------------------------
Index Only Scan using points_p_idx on points
Index Cond: (p <@ '(7,4),(2,1)'::box)
(2 rows)

The consistency function for such an operator (“ indexed-field <@ expression ”, where the indexed-field is a point and the expression is a rectangle) is defined as follows. For an internal record, it returns “yes” if its rectangle intersects with the rectangle defined by the expression. For a sheet entry, the function returns “yes” if its point (“collapsed” rectangle) is contained in the rectangle defined by the expression.



The search begins at the root node. The rectangle (2,1) - (7,4) intersects with (1,1) - (6,3), but does not intersect with (5,5) - (8,8), therefore it is not necessary to go down to the second sub-tree.



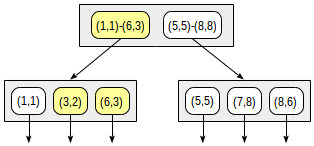
Having come to the leaf node, we sort through the three points contained there and return two of them as a result: (3.2) and (6.3).

postgres=# select * from points where p <@ box '(2,1),(7,4)';
p
-------
(3,2)
(6,3)
(2 rows)


Inside


Regular pageinspect, alas, does not allow a peek inside the GiST index. But there is another way - the extension gevel. It is not included in the standard package; See installation instructions .

If everything is done correctly, three functions will be available to you. First, some statistics:

postgres=# select * from gist_stat('airports_coordinates_idx');
gist_stat
------------------------------------------
Number of levels: 4 +
Number of pages: 690 +
Number of leaf pages: 625 +
Number of tuples: 7873 +
Number of invalid tuples: 0 +
Number of leaf tuples: 7184 +
Total size of tuples: 354692 bytes +
Total size of leaf tuples: 323596 bytes +
Total size of index: 5652480 bytes+

(1 row)

Here you can see that the index on the coordinates of the airport took 690 pages and consists of four levels: the root and two internal levels were shown above in the figures, and the fourth level - sheet.

In fact, the index for eight thousand points will take up much less space: here, for clarity, it was created with a filling of 10%.

Secondly, you can display the index tree:

postgres=# select * from gist_tree('airports_coordinates_idx');
gist_tree
-----------------------------------------------------------------------------------------
0(l:0) blk: 0 numTuple: 5 free: 7928b(2.84%) rightlink:4294967295 (InvalidBlockNumber) +
1(l:1) blk: 335 numTuple: 15 free: 7488b(8.24%) rightlink:220 (OK) +
1(l:2) blk: 128 numTuple: 9 free: 7752b(5.00%) rightlink:49 (OK) +
1(l:3) blk: 57 numTuple: 12 free: 7620b(6.62%) rightlink:35 (OK) +
2(l:3) blk: 62 numTuple: 9 free: 7752b(5.00%) rightlink:57 (OK) +
3(l:3) blk: 72 numTuple: 7 free: 7840b(3.92%) rightlink:23 (OK) +
4(l:3) blk: 115 numTuple: 17 free: 7400b(9.31%) rightlink:33 (OK) +
...

And thirdly, you can display the data itself, which is stored in the index records. Thin point: the result of the function must be converted to the desired data type. In our case, this type is box (bounding box). For example, at the top level we see five entries:

postgres=# select level, a from gist_print('airports_coordinates_idx')
as t(level int, valid bool, a box) where level = 1;
level | a
-------+-----------------------------------------------------------------------
1 | (47.663586,80.803207),(-39.2938003540039,-90)
1 | (179.951004028,15.6700000762939),(15.2428998947144,-77.9634017944336)
1 | (177.740997314453,73.5178070068359),(15.0664,10.57970047)
1 | (-77.3191986083984,79.9946975708),(-179.876998901,-43.810001373291)
1 | (-39.864200592041,82.5177993774),(-81.254096984863,-64.2382965088)
(5 rows)

Actually, the figures above were prepared just on the basis of these data.

Search and ordering operators


The operators considered so far (such as <@ in the predicate p <@ box '(2,1),(7,4)') can be called search operators, since they specify the search conditions in the query.

There is another type of statement - ordering. They are used to indicate the order of results to be output in the order by clause, where simple fields are usually used. Here is an example of such a request:

postgres=# select * from points order by p <-> point '(4,7)' limit 2;
p
-------
(5,5)
(7,8)
(2 rows)


Here p <-> point '(4,7)' is an expression using the ordering operator <-> , which denotes the distance from one argument to another. The meaning of the query: give two points closest to the point (4.7). Such a search is known as k-NN - k-nearest neighbor search.

To support this type of query, the access method must define an additional distance function (distance), and the ordering operator must be included in the appropriate class of operators (for example, for points, the points_ops class). Here is a query that shows the operators and their type (s - search, o - ordering):

postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy
from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop
where opc.opcname = 'point_ops'
and opf.oid = opc.opcfamily
and am.oid = opf.opfmethod
and amop.amopfamily = opc.opcfamily
and am.amname = 'gist'
and amop.amoplefttype = opc.opcintype;
amopopr | amoppurpose | amopstrategy
-------------------+-------------+--------------
<<(point,point) | s | 1
>>(point,point) | s | 5
~=(point,point) | s | 6
<^(point,point) | s | 10
>^(point,point) | s | 11
<->(point,point) | o | 15
<@(point,box) | s | 28
<@(point,polygon) | s | 48
<@(point,circle) | s | 68
(9 rows)

The numbers of the strategies are also shown here with their meaning decoding. It is seen that the strategies are much more than the btree; only part of them is supported for points. For other data types, other strategies may be defined.

The distance function is called for an index element and must determine the distance (taking into account the semantics of the operator) from the value defined by the expression (" indexed-field ordering-operator expression ") to the given element. For a sheet item, this is simply the distance to the indexed value. For an inner element, the function must return the minimum of the distances to the child leaf elements. Since it would be quite expensive to go through all the child records, the function has the right to optimistically minimize the distance, but at the cost of worsening the search efficiency. However, it should not exaggerate categorically - it will break the operation of the index.

The distance function can return a value of any type that can be sorted (to order, PostgreSQL will use comparison semantics from the corresponding family of btree access method operators, as described earlier ).

In the case of points on a plane, the distance is understood in the most usual sense: the value of the expression (x1,y1) <-> (x2,y2) is equal to the root of the sum of the squares of the differences of abscissa and ordinate. For the distance from the point to the bounding rectangle, the minimum distance from the point to this rectangle is taken, or zero if the point is inside it. This value is easy to calculate without circumventing child points, and it is guaranteed not more than the distance to any of the child points.

Consider the search algorithm for the above query.



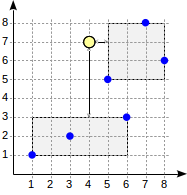
The search begins at the root node. It has two bounding rectangles. The distance to (1.1) - (6.3) is 4.0, and to (5.5) - (8.8) - 1.0.

Bypassing the child nodes occurs in order of increasing distance. Thus, we first go down to the nearest child node and find the distances to the points (for clarity, we will show the figures in the figure):



This information is already enough to return the first two points (5.5) and (7.8). Since we know that the distance to the points inside the rectangle (1,1) - (6,3) is 4.0 or more, there is no need to go down to the first child node.

What if we needed to find the first three points?

postgres=# select * from points order by p <-> point '(4,7)' limit 3;
p
-------
(5,5)
(7,8)
(8,6)
(3 rows)


Although all these points are contained in the second child node, we cannot return (8.6) without looking at the first child node, since there may be closer points (since 4.0 <4.1).



This example explains the distance function requirements for internal records. Choosing a smaller distance for the second record (4.0 instead of real 4.5), we worsened the efficiency (the algorithm began to look through the extra node in vain), but did not break the correctness of the work.

Until recently, GiST was the only access method that could work with ordering operators. But the situation has changed: the RUM method has already been added to this company (about which we will talk later), and it is possible that the good old B-tree will join them - the patch written by our colleague Nikita Glukhov is being discussed by the community.

R-tree for intervals


Another example of using the gist access method is indexing intervals, for example, time (type tsrange). The difference is that the internal nodes of the tree will contain non-bounding rectangles, but bounding intervals.

A simple example. We will rent a house in the village and store in the table the booking intervals:

postgres=# create table reservations(during tsrange);
CREATE TABLE
postgres=# insert into reservations(during) values
('[2016-12-30, 2017-01-09)'),
('[2017-02-23, 2017-02-27)'),
('[2017-04-29, 2017-05-02)');
INSERT 0 3
postgres=# create index on reservations using gist(during);
CREATE INDEX

The index can be used, for example, to speed up the following query:

postgres=# select * from reservations where during && '[2017-01-01, 2017-04-01)';
during
-----------------------------------------------
["2016-12-30 00:00:00","2017-01-08 00:00:00")
["2017-02-23 00:00:00","2017-02-26 00:00:00")
(2 rows)

postgres=# explain (costs off) select * from reservations where during && '[2017-01-01, 2017-04-01)';
QUERY PLAN
------------------------------------------------------------------------------------
Index Only Scan using reservations_during_idx on reservations
Index Cond: (during && '["2017-01-01 00:00:00","2017-04-01 00:00:00")'::tsrange)
(2 rows)

The && operator for intervals denotes the intersection; thus, the request must return all intervals that intersect with the specified one. For such an operator, the consistency function determines whether the specified interval intersects with the value in the inner or leaf entry.

Note that in this case we are not talking about getting the intervals in a certain order, although the comparison operators are defined for the intervals. For them, you can use the b-tree index, but in this case you will have to do without the support of such operations as:

postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy
from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop
where opc.opcname = 'range_ops'
and opf.oid = opc.opcfamily
and am.oid = opf.opfmethod
and amop.amopfamily = opc.opcfamily
and am.amname = 'gist'
and amop.amoplefttype = opc.opcintype;
amopopr | amoppurpose | amopstrategy
-------------------------+-------------+--------------
@>(anyrange,anyelement) | s | 16
<<(anyrange,anyrange) | s | 1
&<(anyrange,anyrange) | s | 2
&&(anyrange,anyrange) | s | 3
&>(anyrange,anyrange) | s | 4
>>(anyrange,anyrange) | s | 5
-|-(anyrange,anyrange) | s | 6
@>(anyrange,anyrange) | s | 7
<@(anyrange,anyrange) | s | 8
=(anyrange,anyrange) | s | 18
(10 rows)

(In addition to equality, which is included in the class of operators for the btree access method.)

Inside


Inside you can look at all the same extension gevel. You just need to remember to change the data type in the call to gist_print:

postgres=# select level, a from gist_print('reservations_during_idx')
as t(level int, valid bool, a tsrange);
level | a
-------+-----------------------------------------------
1 | ["2016-12-30 00:00:00","2017-01-09 00:00:00")
1 | ["2017-02-23 00:00:00","2017-02-27 00:00:00")
1 | ["2017-04-29 00:00:00","2017-05-02 00:00:00")
(3 rows)

Exception restriction


The GiST index can be used to support exclusion constraints.

The exclusion constraint ensures that the specified fields of any two rows of the table will not "match" each other in the sense of some operator. If “equal” is chosen as an operator, then the uniqueness constraint is obtained: the specified fields of any two lines are not equal to each other.

Like the uniqueness constraint, the exception constraint is supported by an index. You can select any operator, if only he:

  1. supported by the index method — the can_exclude property (for example, these are btree, gist, or spgist methods, but not gin);
  2. was commutative, that is, the condition must be satisfied: a operator b =
    b operator a.

Here is a list of suitable strategies and examples of operators (operators, as we remember, may be called differently and may not be available for all data types):


Note that it is possible to use the equality operator in restricting an exception, but it has no practical meaning: the uniqueness restriction will be more efficient. That is why we did not deal with the limitations of the exception when talking about B-trees.

Let us give an example of the use of an exception restriction It is logical not to allow booking a lodge at overlapping time intervals.

postgres=# alter table reservations add exclude using gist(during with &&);
ALTER TABLE

After creating an integrity constraint, we can add lines:

postgres=# insert into reservations(during) values ('[2017-06-10, 2017-06-13)');
INSERT 0 1

But an attempt to insert an overlapping interval into the table will result in an error:

postgres=# insert into reservations(during) values ('[2017-05-15, 2017-06-15)');
ERROR: conflicting key value violates exclusion constraint "reservations_during_excl"
DETAIL: Key (during)=(["2017-05-15 00:00:00","2017-06-15 00:00:00")) conflicts with existing key (during)=(["2017-06-10 00:00:00","2017-06-13 00:00:00")).


Btree_gist extension


Let's complicate the task. Our modest business is expanding and we are going to rent out a few houses:

postgres=# alter table reservations add house_no integer default 1;
ALTER TABLE

We need to change the exclusion constraint to take into account the house number. However, GiST does not support the equality operation for integers:

postgres=# alter table reservations drop constraint reservations_during_excl;
ALTER TABLE
postgres=# alter table reservations add exclude using gist(during with &&, house_no with =);
ERROR: data type integer has no default operator class for access method "gist"
HINT: You must specify an operator class for the index or define a default operator class for the data type.

In this case, the btree_gist extension, which adds GiST support for operations specific to B-trees, will help. In the end, GiST can work with any operators, so why not teach it to work with “more”, “less”, “equal”?

postgres=# create extension btree_gist;
CREATE EXTENSION
postgres=# alter table reservations add exclude using gist(during with &&, house_no with =);
ALTER TABLE

Now we still can not book the first house on the same dates:

postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 1);
ERROR: conflicting key value violates exclusion constraint "reservations_during_house_no_excl"

But we can book a second one:

postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 2);
INSERT 0 1

But you have to understand that, although GiST can somehow work with operations “more”, “less”, “equal”, the B-tree still copes with them better. So this method should be used only if the GiST index is needed essentially - as in our example.

RD-tree for full-text search


About full-text search


Let's start with a minimalist introduction to PostgreSQL full-text search (if you are in the subject, you can skip this section).

The task of full-text search is to select those that match the search query among the set of documents . (If there are a lot of results, then it is important to find the best match, but for now we will keep silent about it.)

The document for the purposes of the search is reduced to a special type tsvector, which contains the tokens and their positions in the document. Lexemes are words converted to a searchable form. For example, standard words are reduced to lower case and their terminating endings are cut off:

postgres=# set default_text_search_config = russian;
SET
postgres=# select to_tsvector(' , . , , .');
to_tsvector
--------------------------------------------------------------------
'':3,5 '':13 '':2 '':9 '':11 '':4 '':7
(1 row)

It also shows that some words (called stop words ) are generally dropped (“and”, “by”), as they are supposed to be found too often for a search on them to be meaningful. Of course, all these transformations are configured, but this is not about that now.

The search query is represented by another type - tsquery. A query, roughly speaking, consists of one or more lexemes connected by logical connectives: “and” & , “or” | , "Not" ! . You can also use parentheses to specify the priority of operations.

postgres=# select to_tsquery(' & ( | )');
to_tsquery
----------------------------------
'' & ( '' | '' )
(1 row)

For full-text search, a single match operator @@ is used.

postgres=# select to_tsvector(' , .') @@ to_tsquery(' & ( | )');
?column?
----------
t
(1 row)

postgres=# select to_tsvector(' , .') @@ to_tsquery(' & ( | )');
?column?
----------
f
(1 row)

This information will be enough for now. Let's talk a little bit more about full-text search in one of the following parts on the GIN index.

Rd trees


In order for full-text search to work quickly, you must firstly store a tsvector column in the table (so as not to perform an expensive conversion each time you search), and second, build an index on this field. One of the possible access methods for this is GiST.

postgres=# create table ts(doc text, doc_tsv tsvector);
CREATE TABLE
postgres=# create index on ts using gist(doc_tsv);
CREATE INDEX
postgres=# insert into ts(doc) values
(' '), (' '), (', , '),
(' '), (' '), (', , '),
(' '), (' '), (', , ');
INSERT 0 9
postgres=# update ts set doc_tsv = to_tsvector(doc);
UPDATE 9

The last step (conversion of the document in tsvector), of course, is convenient to assign to the trigger.

postgres=# select * from ts;
doc | doc_tsv
-------------------------+--------------------------------
| '':3 '':2 '':4
| '':3 '':2 '':4
, , | '':1,2 '':3
| '':2 '':3 '':1
| '':3 '':2 '':1
, , | '':3 '':1,2
| '':3 '':2
| '':1 '':2 '':3
, , | '':3 '':1,2
(9 rows)

How should the index be arranged? Directly R-tree is not suitable here - it is not clear what a “bounding box” is for documents. But you can apply some modification of this approach for sets - the so-called RD-tree (RD is the Russian Doll, the nested doll). By set in this case, we understand the set of document lexemes, but in general a set can be any.

The idea of ​​RD-trees is to take a bounding set instead of a bounding box — that is, a set containing all elements of the child sets.

An important question is how to represent sets in index records. Probably the most straightforward way is to simply list all the elements of a set. Here’s how it might look:



Then, for example, for access by condition, doc_tsv @@ to_tsquery('') could be lowered only to those nodes that have the lexeme 'standing':



The problems of such a presentation are quite obvious. The number of tokens in a document can be quite large, so index entries will take up a lot of space and fall into TOAST, making the index much less efficient. Even if there are some unique tokens in each document, the union of the sets can still be very large - the higher to the root, the greater will be the index entries.

Such a representation is sometimes used, but for other data types. And for a full-text search, a different, more compact solution is used - the so-called signature tree. His idea is well known to all who dealt with the Bloom filter.

Each token can be represented by its signature: a bit string of a certain length, in which all the bits are zero, except for one. The number of this bit is determined by the value of the hash function of the lexeme (about how the hash functions are arranged, we said earlier ).

The document signature is called the bitwise “or” signatures of all the tokens of the document.

Suppose the signatures of our tokens are:

1000000
0001000
0000010
0010000
0000100
0100000
0000100
0000001
0000010
0000010
0010000

Then the document signatures are obtained as follows:

0011010
0010110
, , 0110000
0011100
0010100
, , 0110000
0000011
1001010
, , 0100010


The index tree can be represented as follows:



The advantages of this approach are obvious: index records have the same and small size, the index is compact. But the drawback is also visible: because of the compactness, accuracy is lost.

Consider the same condition doc_tsv @@ to_tsquery('') . We calculate the search query signature in the same way as for the document: in our case, 0010000. The consistency function must output all the child nodes whose signature contains at least one bit from the query signature:



Compare with the picture above: it is clear that the tree is “yellowed” - and this means that false positive responses occur (what we call errors of the first kind) and extra nodes are searched during the search. Here we hooked the lexeme “zalomat”, the signature of which, in misfortune, coincided with the signature of the sought lexeme “standing”. It is important that false negatives (errors of the second kind) in this scheme can not be, that is, we are guaranteed not to miss the desired value.

In addition, it may happen that different documents will get the same signatures: in our example, there were no luck “people, people, standing” and “people, people, zalomati” (both have signature 0110000). And if the tsvector value itself is not stored in the leaf index record, then the index itself will give false positives. Of course, in this case, the access method will ask the index mechanism to recheck the result on the table, so that the user will not see these false positives. But the effectiveness of the search may well suffer.

In fact, the signature in the current implementation takes 124 bytes instead of seven bits in our pictures, so the probability of collisions is significantly less than in the example. But after all, the documents in practice are indexed much more. In order to somehow reduce the number of false positives of the index method, the implementation goes to the trick: the indexed tsvector is stored in the leaf index record, but only if it does not take up much space (just under 1/16 of a page, which is about half a kilobyte for 8 KB pages) .

Example


To see how indexing works on real data, take the pgsql-hackers mailing list archive. The version used in the example contains 356,125 letters with the departure date, subject, author and text:

fts=# select * from mail_messages order by sent limit 1;
-[ RECORD 1 ]------------------------------------------------------------------------
id | 1572389
parent_id | 1562808
sent | 1997-06-24 11:31:09
subject | Re: [HACKERS] Array bug is still there....
author | "Thomas G. Lockhart" <Thomas.Lockhart@jpl.nasa.gov>
body_plain | Andrew Martin wrote: +
| > Just run the regression tests on 6.1 and as I suspected the array bug +
| > is still there. The regression test passes because the expected output+
| > has been fixed to the *wrong* output. +
| +
| OK, I think I understand the current array behavior, which is apparently+
| different than the behavior for v1.0x. +
...

Add and fill the tsvector type column and build the index.Here we will combine the three values ​​(subject, author and text of the letter) into one vector to show that the document does not have to be a single field, but may consist of completely arbitrary parts. Some words, apparently, were rejected due to too large size. But in the end, the index is built and ready to support search queries: Here you can see that, along with 898 matching lines, the access method returned another 7859 rows, which were eliminated by rechecking on the table. This clearly shows the negative impact of loss of accuracy on efficiency.

fts=# alter table mail_messages add column tsv tsvector;
ALTER TABLE
fts=# update mail_messages
set tsv = to_tsvector(subject||' '||author||' '||body_plain);
NOTICE: word is too long to be indexed
DETAIL: Words longer than 2047 characters are ignored.
...
UPDATE 356125
fts=# create index on mail_messages using gist(tsv);
CREATE INDEX



fts=# explain (analyze, costs off)
select * from mail_messages where tsv @@ to_tsquery('magic & value');
QUERY PLAN
----------------------------------------------------------
Index Scan using mail_messages_tsv_idx on mail_messages
(actual time=0.998..416.335 rows= 898 loops=1)
Index Cond: (tsv @@ to_tsquery('magic & value'::text))
Rows Removed by Index Recheck: 7859
Planning time: 0.203 ms
Execution time: 416.492 ms
(5 rows)



Inside


To analyze the contents of the index, we again use the gevel extension: Values ​​of a special type of gtsvector stored in index records are the signature itself, plus possibly the original tsvector. If there is a vector, then the number of tokens in it (unique words) is displayed, and if not, then the number of set (true) and cleared (false) bits in the signature. It can be seen that in the root node the signature has degenerated to “all units” - that is, one index level has become completely useless (and another one is almost completely useless with only four bits dropped).

fts=# select level, a from gist_print('mail_messages_tsv_idx') as t(level int, valid bool, a gtsvector) where a is not null;
level | a
-------+-------------------------------
1 | 992 true bits, 0 false bits
2 | 988 true bits, 4 false bits
3 | 573 true bits, 419 false bits
4 | 65 unique words
4 | 107 unique words
4 | 64 unique words
4 | 42 unique words
...





Properties


Let's take a look at the properties of the gist access method (requests were cited earlier ): There is no support for sorting values ​​and uniqueness. The index, as we have seen, can be built on several columns and used in the exception constraints. Index Properties: And, the most interesting, column level properties. Some properties will be permanent: (No sorting support; index cannot be used to search in an array; undefined values ​​are supported.) But the two remaining properties, distance_orderable and returnable, will depend on the class of operators used. For example, for points see:

amname | name | pg_indexam_has_property
--------+---------------+-------------------------
gist | can_order | f
gist | can_unique | f
gist | can_multi_col | t
gist | can_exclude | t





name | pg_index_has_property
---------------+-----------------------
clusterable | t
index_scan | t
bitmap_scan | t
backward_scan | f



name | pg_index_column_has_property
--------------------+------------------------------
asc | f
desc | f
nulls_first | f
nulls_last | f
orderable | f
search_array | f
search_nulls | t





name | pg_index_column_has_property
--------------------+------------------------------
distance_orderable | t
returnable | t

The first property says that the distance operator is available to search for the nearest neighbors. And the second is that the index can be used exclusively in index scanning. In spite of the fact that not points, but rectangles are stored in leaf index records, the access method is able to return what is needed.

But the intervals: For them, the distance function is not defined, hence the search for the nearest neighbors is impossible. And full text search:

name | pg_index_column_has_property
--------------------+------------------------------
distance_orderable | f
returnable | t





name | pg_index_column_has_property
--------------------+------------------------------
distance_orderable | f
returnable | f

The ability to perform only index scans was also lost here, since only a signature without the actual data can appear in the leaf records. However, this is a small loss, since the value of the tsvector type still does not interest anyone: it is used to select rows, but you need to show the source text, which is still not in the index.

Other data types


Finally, we will denote several more types that are currently supported by the GiST access method, in addition to the geometrical types we have already examined (using dots for example), ranges, and full-text search types.

Of the standard types, these are IP addresses inet , and the rest is added by extensions:

Continued .

Source: https://habr.com/ru/post/333878/

More articles:


All Articles