Fast data recovery. Regeneration butterfly pattern

For the codes described in the previous article about data recovery , a problem formulation was assumed, which minimizes the number of disks required for a recovery operation. In [2], the use of network coding to data storage problems is discussed, which has received considerable attention from researchers in recent years. Here it is not the optimization of the number of disks required for data recovery, but the minimization of the network traffic that occurs.

Suppose the storage system consists of n nodes. Consider a file consisting of B characters of the GF (q) field, which is encoded in nα characters over GF (q) and distributed among the nodes, so that each node stores α characters. The code is constructed in such a way that the data can be completely recovered from information from k nodes. In this case, to restore the data of a single node, it suffices to obtain β ≤ α information from d nodes [1,2], see fig. 1. The value γ = dβ is called the repair bandwidth.

In [2] it is shown that the size of data B is bounded above:

$$

$$B \ le \ sum_ {i = 0} ^ {k-1} min \ {α, (d-i) β \}$$

Figure 1. Regeneration Code
')
For fixed values ​​( B, k, d ) there is a set of pairs (α, β) that satisfy this boundary, which makes it possible to obtain a compromise on these parameters, with two extreme points: minimizing the value of the common storage nα (this point is called “recovery with minimum storage, ”or MSR , Minimum Storage Regeneration) and minimizing the range γ = dβ (this point is called“ recovery with a minimum range, ”or MBR , Minimum Bandwidth Regeneration). Codes that satisfy the above boundary are called regenerating codes. An example of the corresponding boundary is shown in Fig. 2 [2].


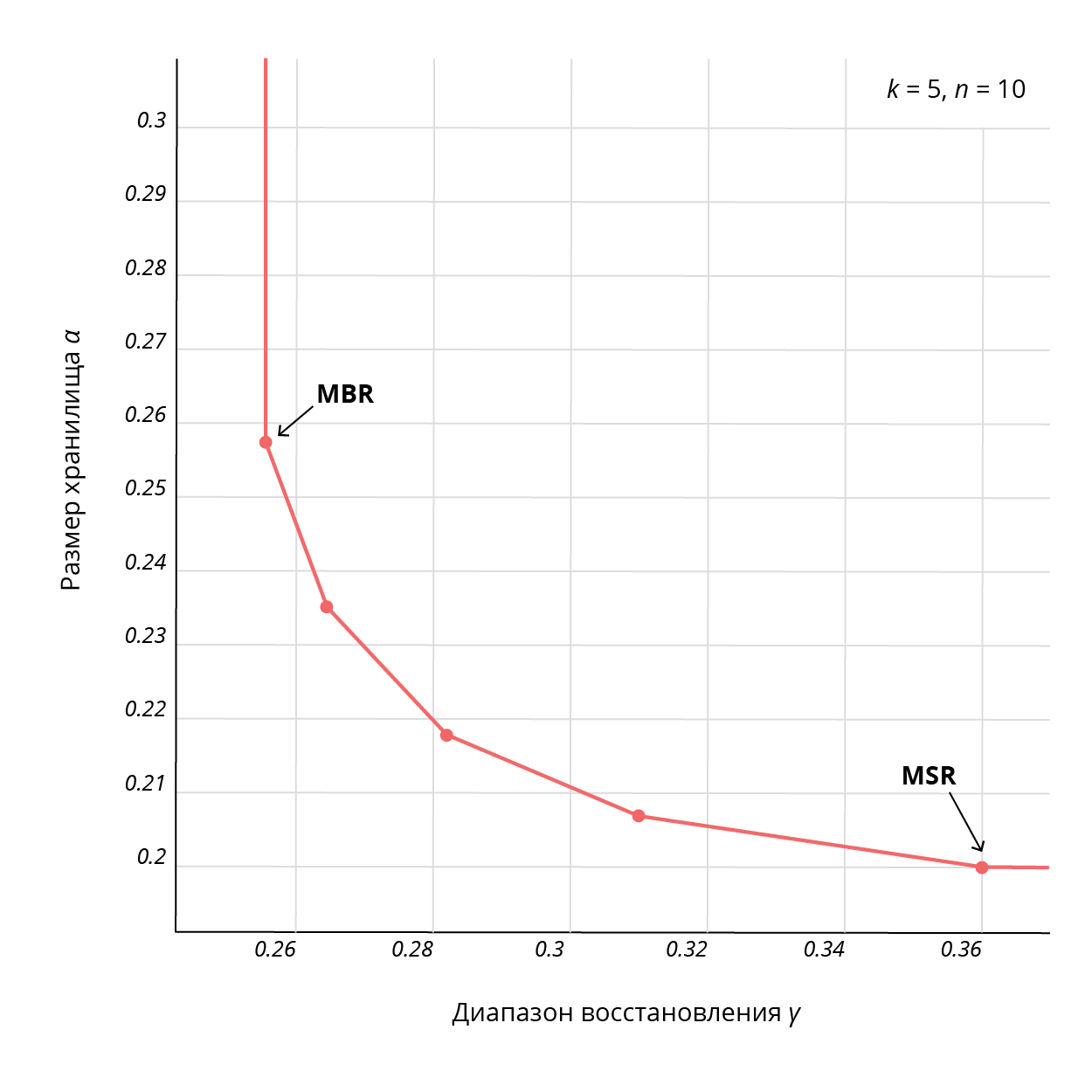
Fig. 2. MSR-MBR curve for regenerating codes

In recent years, considerable attention has been paid to the construction of codes at the MSR and MBR points, as well as codes that lie at intermediate points of the boundary [3, 6, 7]. Various designs of regenerating codes can also be found in [8-15]. The main disadvantage of these codes is poor scalability.

We optimized one of the types of regenerating codes - “butterfly” [4] (this code is systematic, it is very important for requests like random reading) for fast recovery of a single disk and improved the scalability of this design.

Butterfly coding scheme

Consider the sequence of $$$2 ^ {n-1}$stripes, where n is the number of data disks. The data of this set of stripes is encoded using XOR codes. The first checksum ( h ) is calculated on blocks with the same LBA on all data disks: $$$(h_i = \ sum_ja_j, i)$. The second - according to the Butterfly-scheme presented in Figure 3.


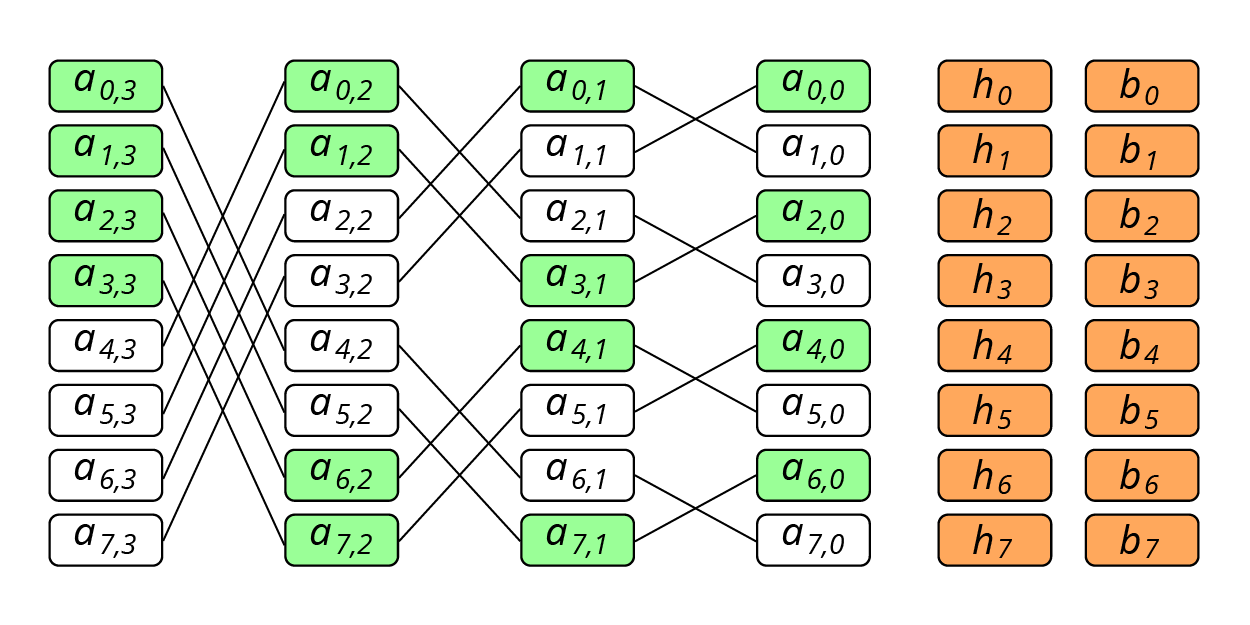
Fig. 3. Butterfly coding scheme

For example, the calculation of the checksum $$$b_3$performed as XOR blocks $$$a_ {3,0}, a_ {2,1}, a_ {0,2}, a_ {4,3}$. In addition, the color of the block also has a value, which is defined as: if the j- th bit in the binary representation of the number i matches its ( j-1 ) -th bit, then the block $$$a_ {j, i}$will be green. For a zero component, all even-numbered blocks will be green.

If there are green blocks in the resulting set, for each of them it is necessary to include a block to the right of it in the set. In other words, if a block $$$a_ {j, i}$from the main set - green, the block is also included in the set $$$a_ {j-1, i}$. For the blocks included in the set in this way, the color does not matter. Therefore, the calculation formula for $$$b_3$will be like this:

$$

$$b_3 = a_ {3,0} + a_ {2,1} + a_ {0,2} + a_ {0,1} + a_ {4,3}$$

The choice of just such a coding method is justified in [4]. This guarantees the recovery of two simultaneously failed components.

Using this coding method to restore a component with read data will require less. Namely, to recover $$$2 ^ {n-1}$blocks of the failed storage component will need to be read $$$(n + 1) ⋅2 ^ {n-2}$units, which in the limit reduces the number of reads compared to RAID-6 in 2 times.

However, if the node containing the checksum fails, recovery will need to read all the data, and in this case there will be no gain. This problem can be solved with a shift similar to a shift in RAID-6, or with randomization, which we have already used in the approach with local reconstruction codes . If in each set of $$$2 ^ {n-1}$stripes to make a random permutation, then the readings necessary to handle cases of component failures with checksums will be evenly distributed across all options for failures.

It is also necessary to understand that the regenerating codes have one major drawback: a strict limitation on the number of blocks in the stripe. For a disk array, this is irrelevant, because the size of the encoded block may vary, and therefore, their number may vary. But for a cluster configuration, in the node where the number of disks may be limited, the problem of scaling needs to be solved. One of the possible solutions is splitting the stripe into regenerating groups. This will increase redundancy as many times as there will be groups, but the coding sets themselves will become exponentially smaller, see fig. four.


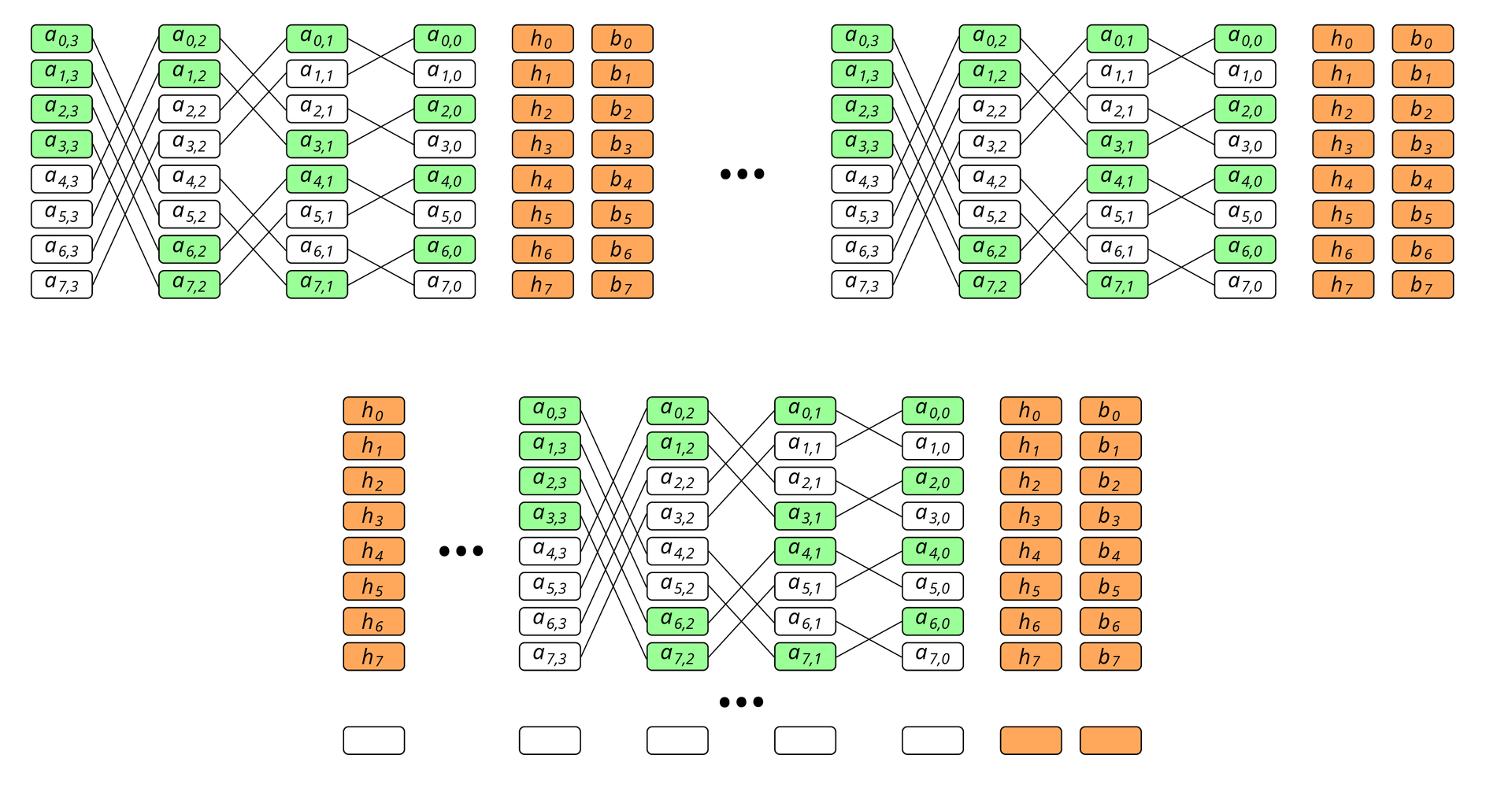
Fig. 4. Exponential reduction of stripes of the coded set

Finally, the last thing to consider when applying regenerating codes is the area into which information from the failed disk will be restored. The fact is that when restoring to a hot-spare disk, the recovery speed will be limited by the write speed to it, and a decrease in the number of readings will not give a significant gain. Therefore, there is a need to include an empty-block in the stripe.

Performance testing

To test the performance, we created a RAID of 22 disks with specific layouts. A RAID device was created using a device-mapper modification that changed the addressing of a block of data according to a specific algorithm. Data was recorded on the RAID array, and checksums were calculated for later recovery. A failed disk was selected. Data recovery was performed either to the corresponding empty blocks or to the hot spare disk. We compared the following schemes:

• RAID-6 is a classic RAID-6 with two checksums, data recovery on a hot spare disk.
• RAID-6E - RAID6 c empty block at the end of the stripe, data recovery on empty blocks of the corresponding stripe.
• Classic LRC + E - LRC scheme in which local groups go sequentially and end with a checksum, recovery to an empty block.
• LRC rand - to generate each LRC stripe, its number is used as the core of the random number generator, data recovery to an empty block.
• Classic Regen is a circuit with three groups of regenerating codes.
• Regen rand is a circuit with three groups of regenerating codes and randomization, data recovery to an empty block.

22 disks with the following characteristics were used for testing:

• MANUFACTURER: IBM
• PART NUMBER: ST973452SS-IBM
• CAPACITY: 73GB
• INTERFACE: SAS
• SPEED: 15K RPM
• SIZE FORM FACTOR: 2.5IN

When testing performance, the size of the stripe blocks has a big effect. When restoring, reading from disks is done at increasing addresses (sequentially), but due to declustering in random layouts, some blocks are skipped. This means that if the blocks are small, the positioning of the magnetic disk head will be done very often, and this will adversely affect the performance. Since the specific values ​​of the data recovery speed may depend on the hard drive model, manufacturer, RPM, we presented the results in relative terms. Figure 5 shows how the performance gains come from (b) - (f) compared to classic RAID-6.


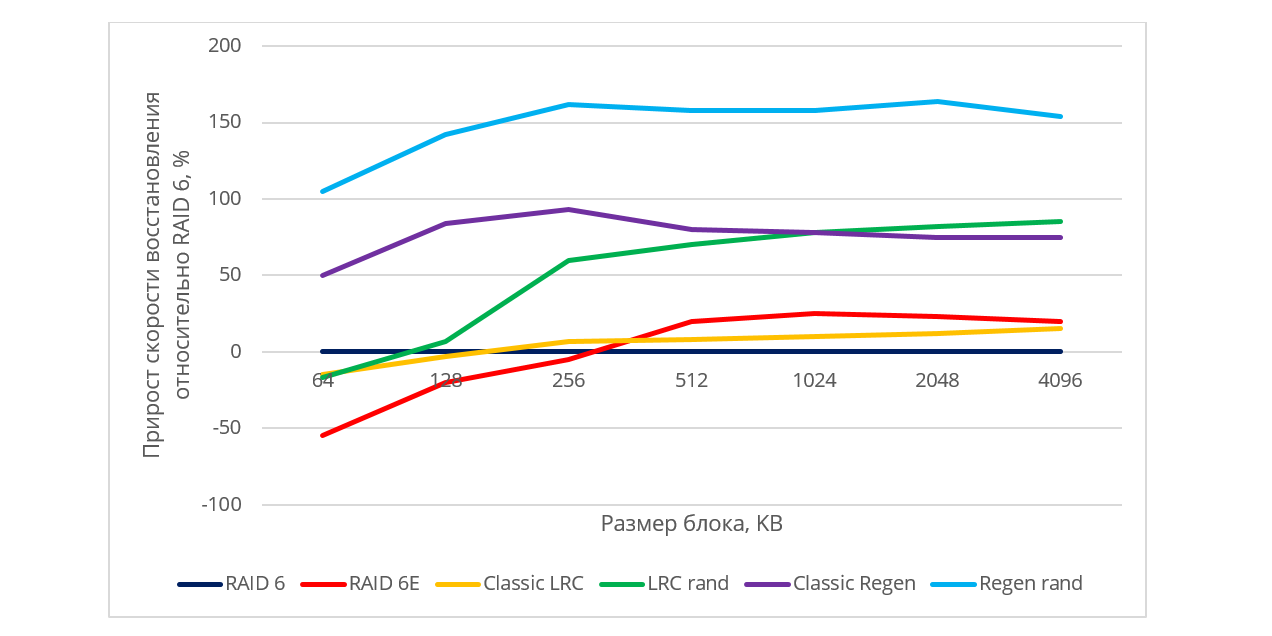
Fig. 5. Relative performance of various placement algorithms

When restoring data to a hot spare disk, we received that the recovery speed is limited by the speed of writing to disk for all circuits using hot spare. It can be noted that both the randomized LRC scheme and the regenerative codes give a rather high increase in the recovery rate compared to the non-optimal and RAID-6. Despite the fact that the regenerating codes clearly lead in the recovery rate, their main disadvantages cannot be ignored: the limitation on the number of blocks in the encoded set and high redundancy: with the empty-block in the checked configuration, redundancy was more than 30% (Fig. 6).


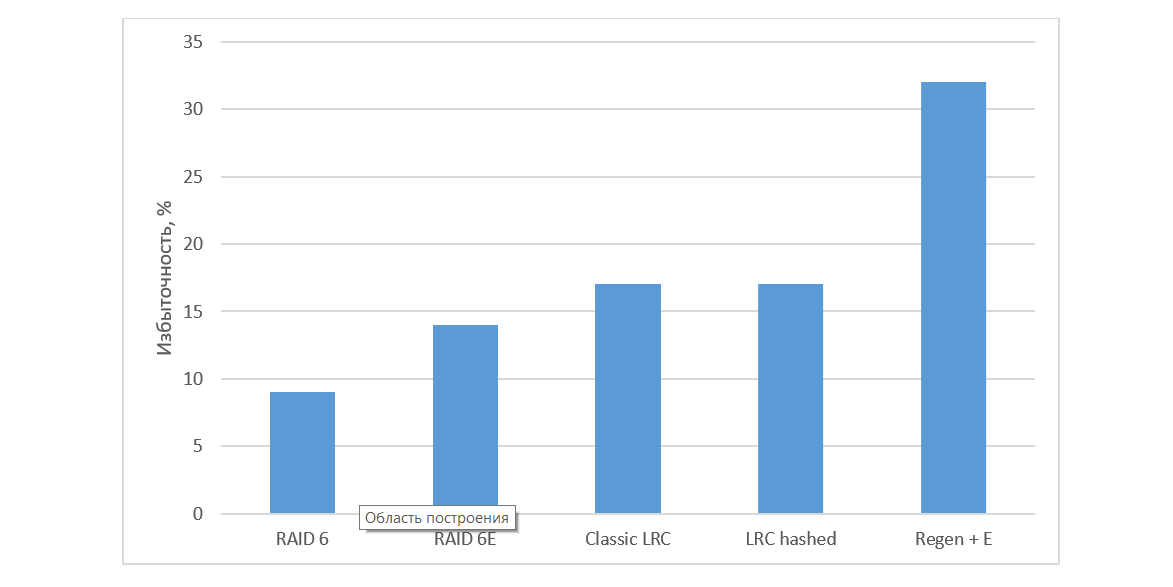
Fig. 6. Redundancy of various algorithms

Conclusion

Regenerating Butterfly-codes were successfully tested in HDFS, Ceph [5].

We considered the options for using regenerating codes on a local system, came up with a way to scale them and use them to quickly handle a single disk failure situation.

Despite the fact that the performance of this solution turned out to be the best (see Fig. 5), the requirements for redundancy (see Fig. 6) can be costly, therefore this algorithm is not suitable everywhere. Thus, it is always necessary to understand whether in a particular case one can sacrifice a place for the sake of reliability.

The presented solutions can be generalized to distributed, in particular - cloud storage system. In such systems, the advantages will be even more pronounced, since in them the bottleneck is the transmission of data over the network, which can be minimized through the presented approaches.