Using Neural Networks to Recognize Handwritten Numbers Part 1

Hi, Habr! In this series of articles I will give a brief translation from English of the first chapter of Michael Nilsson’s book "Neural Networks and Deep Learning".

I have broken the translation into several articles on Habrr to make it easier to read:

Part 1) Introduction to Neural Networks

Part 2) Construction and Gradient Descent

Part 3) Network implementation for digit recognition

Part 4) A bit about deep learning

Introduction

The human visual system is one of the most amazing in the world. In each hemisphere of our brain there is a visual cortex containing 140 million neurons with dozens of billions of connections between them, but such a cortex is not one, there are several of them, and together they form a real supercomputer in our head, best adapted during the evolution to the perception of the visual component of our world. But the difficulty of recognizing visual images becomes obvious if you try to write a program for recognizing, say, handwritten numbers.

A simple intuition - “a 9-piece has a loop on the top, and a vertical tail below” is not so easy to implement algorithmically. Neural networks use examples, derive some rules and learn from them. Moreover, the more examples we show the network, the more she learns about handwritten numbers, therefore she classifies them with greater accuracy. We will write a program in 74 lines of code that will determine handwritten numbers with an accuracy of> 99%. So let's go!

Perceptron

What is a neural network? To begin, explain the model of an artificial neuron. Perceptron was developed in 1950 by Frank Rosenblat , and today we will use one of its main models, the sigmoid perceptron. So how does it work? Persepron takes on the input vector $$$\ bar {x} = \ left \ {x_ {1}, x_ {2}, x_ {3}, ..., x_ {N} \ right \}, x_ {i} \ in \ mathbb {R}$ and returns some output value $$$output \ in \ mathbb {R}$.

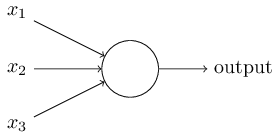
Rosenblat proposed a simple rule for calculating the output value. He introduced the concept of "significance", then the "weight" of each input value $$$\ bar {w} = \ left \ {w_ {1}, w_ {2}, w_ {3}, ..., w_ {N} \ right \}, w_ {i} \ in \ mathbb {R}$ . In our case $$$output$will depend on whether $$$\ sum_ {i = 1} ^ {N} x_ {i} w_ {i}$greater than or less than a certain threshold $$$threshold \ in \ mathbb {R}$.

$$

$$output = \ begin {cases} 0 & \ text {if} \ sum_ {i = 1} ^ {N} x_ {i} w_ {i} \ leq threshold \\ 1 & \ text {if} \ sum_ {i = 1} ^ {N} x_ {i} w_ {i}> threshold \ end {cases}$$

And that's all we need! Varying $$$threshold$and the scale vector $$$\ bar {w}$You can get completely different decision models. Now back to the neural network.

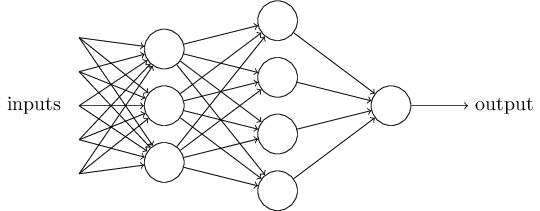
So, we see that the network consists of several layers of neurons. The first layer is called the input layer or receptors ( $$$Receptors, InputLayer$), the next layer is hidden ( $$$HiddenLayer$), and the last is the output layer ( $$$OutputLayer$). Condition $$$\ sum_ {i = 1} ^ {N} x_ {i} w_ {i}> threshold$rather cumbersome let's replace $$$\ sum_ {i = 1} ^ {N} x_ {i} w_ {i}$on the dot product of vectors $$$\ bar {x} \ cdot \ bar {w}$. Next we set $$$b = -threshold$let's call it the displacement of the perceptron or $$$bias$and transfer $$$b$to the left side. We get:

$$

$$output = \ begin {cases} 0 & \ text {if} \ bar {x} \ cdot \ bar {w} + b \ leq 0 \\ 1 & \ text {if} \ bar {x} \ cdot \ bar {w} + b> 0 \ end {cases}$$

Learning problem

To find out how learning can work, suppose that we have slightly changed some weight or network offset. We want this small weight change to cause a small corresponding change at the exit of the network. Schematically it looks like this:

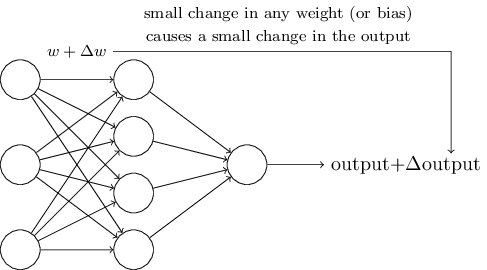
If this were possible, we could manipulate the weights in the direction advantageous to us and gradually train the network, but the problem is that with some change in the weight of a particular neuron - its output can completely “roll over” from 0 to 1. This can lead to a large forecast error of the entire network, but there is a way around this problem.

Sigmoid neuron

We can overcome this problem by introducing a new type of artificial neuron, called a sigmoid neuron. Sigmoid neurons are similar to perceptrons, but are modified so that small changes in their weights and displacement cause only a small change in their output. The structure of the sigmoid neuron is similar, but now it can take as input $$$0 \ leq x_ {i} \ leq 1, \ forall x_ {i} \ in \ bar {x}$, and on the output issue $$$\ sigma (\ bar {x} \ cdot \ bar {w} + b)$where

$$

$$\ begin {eqnarray} \ sigma (z) = \ frac {1} {1 + e ^ {- z}}. \ end {eqnarray}$$

It would seem that there are completely different cases, but I assure you that the perceptron and the sigmoid neuron have much in common. Assume that $$$z = \ bar {x} \ cdot \ bar {w} + b \ rightarrow \ infty$then $$$e ^ {- z} \ rightarrow 0$and therefore $$$\ sigma (z) \ rightarrow 1$. The converse is true if $$$z = \ bar {x} \ cdot \ bar {w} + b \ rightarrow - \ infty$then $$$e ^ {- z} \ rightarrow \ infty$and $$$\ sigma (z) \ rightarrow 0$. Obviously, when working with a sigmoid neuron, we have a smoother perceptron. And really:

$$

$$\ Delta output \ approx \ sum_ {i = 1} ^ {N} \ frac {\ partial output} {\ partial w_ {i}} \ Delta w_ {i} + \ frac {\ partial output} {\ partial b } \ Delta b$$

Neural Network Architecture

Designing the input and output layers of a neural network is quite an exercise. For example, suppose we are trying to determine whether the handwritten "9" is depicted in the image or not. A natural way to design a network is to encode the image pixel intensities into the input neurons. If the image has a size $$$64 \ cdot 64$then we have $$$4,096 = 64 \ cdot $ 6$input neuron. The output layer has one neuron, which contains the output value, if it is greater than 0.5, then there is “9” in the image, otherwise there isn’t. While designing input and output layers is a fairly simple task, the choice of architecture for hidden layers is art. Researchers have developed many heuristics for designing hidden layers, such as those that help compensate for the number of hidden layers versus network learning time.

So far, we have used neural networks, in which the output from one layer is used as a signal for the next, such networks are called direct neural networks or direct distribution networks ( $$$FeedForward$). However, there are other models of neural networks in which feedback loops are possible. These models are called recurrent neural networks ( $$$Recurrent Neural Network$). Recurrent neural networks were less influential than direct-connected networks, in part because learning algorithms for recurrent networks (at least for today) are less effective. But recurrent networks are still extremely interesting. They are much closer in spirit to how our brain works than networks with direct communication. And it is quite possible that repetitive networks can solve important problems that can be solved with great difficulty using direct access networks.

So, for today everything, in the following article I will tell about gradient descent and training of our future network. Thanks for attention!