Exact calculation of averages and covariances by the Welford method

The Welford method is a simple and efficient way to calculate averages, variances, covariances, and other statistics. This method has a number of excellent properties:

• achieves excellent performance in precision solutions;
• it is extremely easy to remember and implement;
• This is a single-pass online algorithm, which is extremely useful in some situations.

The original article by Welford was published in 1962. Nevertheless, it is impossible to say that the algorithm is somehow widely known at the present time. And to find a mathematical proof of its correctness or experimental comparisons with other methods is not at all trivial.

This article attempts to fill these gaps.

Content

• Introduction
• 1. Errors in the calculation of the average
• 2. Legend
• 3. Calculation of averages
• 4. Calculation of covariances
• 5. Experimental comparison of methods
• Conclusion

Introduction

In the first months of my work as a developer, I was developing a machine learning method in which decision trees with linear regression models in the leaves were subjected to gradient boostering. This algorithm was chosen partly in spite of the fashionable then-winning concept of today to build huge compositions of very simple algorithms: on the contrary, we wanted to build small compositions of rather complex models.

The topic itself turned out to be so interesting for me that I later even wrote a thesis about it. To build a model of several hundred trees, one has to solve a linear regression problem tens of thousands of times, and it turned out to be difficult to achieve good quality in all cases, because the data for these models are very diverse, and the problems of multicollinearity, regularization and computational accuracy rise to full height. But one bad model in one leaf of one tree is enough for the whole composition to be completely unsuitable.

In the process of solving the problems associated with the automatic construction of a huge number of linear models, I managed to find out a number of facts that were useful to me later in a variety of situations, including those not related to the linear regression problem itself. Now I want to talk about some of these facts, and first I decided to talk about the method of Welford.

The article has the following structure. In paragraph 1, we consider the simplest task of computing the average, for example, we understand that this problem is not as simple as it seems at first glance. Paragraph 2 introduces the notation used in this article, which will be useful in sections 3 and 4 , devoted to the derivation of the Welford method formulas for, respectively, the calculation of weighted averages and weighted covariances. If you are not interested in the technical details of formulas output, you can skip these sections. Paragraph 5 contains the results of an experimental comparison of methods, and in conclusion is an example of the implementation of algorithms in C ++.

The model code for comparing methods for calculating the covariance is in my github project . A more complex code, in which the Welford method is used to solve a linear regression problem, is in another project , which will be discussed in the following articles.

1. Errors in the calculation of the average

I'll start with a classic example. Let there be a simple class that calculates the average for a set of numbers:

class TDummyMeanCalculator { private: float SumValues = 0.; size_t CountValues = 0; public: void Add(const float value) { ++CountValues; SumValues += value; } double Mean() const { return CountValues ? SumValues / CountValues : 0.; } }; 

Let's try to put it into practice in the following way:

 int main() { size_t n; while (std::cin >> n) { TDummyMeanCalculator meanCalculator; for (size_t i = 0; i < n; ++i) { meanCalculator.Add(1e-3); } std::cout << meanCalculator.Mean() << std::endl; } return 0; } 

What will the program output?

Input	Conclusion
10,000	0.001000040
1,000,000	0.000991142
100,000,000	0.000327680
20,000,000	0.000163840
300000000	0.000109227

Starting from a certain moment, the sum ceases to change after the addition of the next term: this happens when SumValues is equal to 32768, since to represent the result of the summation to the type float simply not enough bit.

There are several ways out of this situation:

1. Jump from float to double .
2. Use one of the more complex summation methods .
3. Use the Kahan method for summation.
4. Finally, you can use the Welford method to directly calculate the average.

It is not so easy to find data on which a solution using a double doesn't work well. However, such data is found, especially in more complex tasks. It is also frustrating that using double increases memory costs: sometimes you need to store a large number of averages at the same time.

Kahan’s methods and other complex summation methods are good in their own way, but in the future we will see that the Welford method still works better, and, besides, it is surprisingly simple to implement. Indeed, let's look at the corresponding code:

 class TWelfordMeanCalculator { private: float MeanValues = 0.; size_t CountValues = 0; public: void Add(const float value) { ++CountValues; MeanValues += (value - MeanValues) / CountValues; } double Mean() const { return MeanValues; } }; 

On the question of the correctness of this code, we will return in the future. In the meantime, we note that the implementation looks quite simple, but on those data that are used in our program, it also works with perfect accuracy. This is due to the fact that the difference value - MeanValues at the first iteration is exactly equal to the average, and at subsequent iterations is equal to zero.

This example illustrates the main advantage of the Welford method: all quantities involved in arithmetic operations are “comparable” in magnitude, which, as is well known, contributes to good accuracy of calculations.

Input	Conclusion
10,000	0.001
1,000,000	0.001
100,000,000	0.001
20,000,000	0.001
300000000	0.001

In this article we will consider the application of the Welford method to another problem - the problem of calculating covariance. In addition, we will compare various algorithms and obtain mathematical proofs of the correctness of the method.

2. Legend

The derivation of a formula can often be made very simple and straightforward if you choose the correct notation. We will try and we. We assume that two sequences of real numbers are given: $$$x$ and $$$y$ and the sequence of their respective weights $$$w$ :

$$

$$x = x_1, x_2, ..., x_n, ...$$

$$

$$y = y_1, y_2, ..., y_n, ...$$

$$

$$w = w_1, w_2, ..., w_n, ...$$

Since we want to calculate averages and covariances, we will need notation for weighted sums and sums of products. We will try to describe them in the same way:

$$

$$S_n ^ {a, b, ..., z} = \ sum_ {i = 1} ^ n {a_i \ cdot b_i \ cdot ... \ cdot z_i}$$

Then, for example, $$$S_n ^ {w}$ Is the sum of the weights of the first $$$n$ elements $$$S_n ^ {wx}$ - this is a weighted sum of the first $$$n$ the numbers of the first sequence, and $$$S_n ^ {wxy}$ - the sum of weighted products:

$$

$$S_n ^ {w} = \ sum_ {i = 1} ^ n {w_i}$$

$$

$$S_n ^ {wx} = \ sum_ {i = 1} ^ n {w_i \ cdot x_i}$$

$$

$$S_n ^ {wxy} = \ sum_ {i = 1} ^ n {w_i \ cdot x_i \ cdot y_i}$$

We also need average weights:

$$

$$m_n ^ {wx} = \ frac {\ sum_ {i = 1} ^ n {w_i \ cdot x_i}} {\ sum_ {i = 1} ^ n {w_i}} = \ frac {S_n ^ {wx}} {S_n ^ w}$$

$$

$$m_n ^ {wy} = \ frac {\ sum_ {i = 1} ^ n {w_i \ cdot y_i}} {\ sum_ {i = 1} ^ n {w_i}} = \ frac {S_n ^ {wy}} {S_n ^ w}$$

Finally, we introduce the notation for non-normalized "scatter" $$$D_ {n} ^ {wxy}$ and normalized covariances $$$C_ {n} ^ {wxy}$ :

$$

$$D_ {n} ^ {wxy} = \ sum_ i = 1} ^ {n} w_i (x_i - m_ {n} ^ {wx}) (y_i - m_ {n} ^ {wy})$$

$$

$$C_ {n} ^ {wxy} = \ frac {D_ {n} ^ {wxy}} {S_ {n} ^ w} = \ frac {\ sum_ {i = 1} ^ {n} w_i (x_i - m_ {n} ^ {wx}) (y_i - m_ {n} ^ {wy})} {\ sum_ {i = 1} ^ {n} w_ {i}}$$

3. Calculation of averages

Let us prove a weighted analogue of the formula we used above to calculate the average by the Welford method. Consider the difference $$$m_ {n + 1} ^ {wx} - m_ {n} ^ {wx}$ :

$$

$$m_ {n + 1} ^ {wx} - m_ {n} ^ {wx} = \ frac {S_ {n + 1} ^ {wx}} {S_ {n + 1} ^ {w}} - \ frac {S_ {n} ^ {wx}} {S_ {n} ^ {w}} = \ frac {S_ {n} ^ {w} S_ {n + 1} ^ {wx} - S_ {n} ^ {wx } S_ {n + 1} ^ {w}} {S_ {n + 1} ^ {w} S_ {n} ^ {w}} =$$

$$

$$= \ frac {S_ {n} ^ {w} S_ {n} ^ {wx} + w_ {n + 1} x_ {n + 1} S_n ^ w - S_ {n} ^ {wx} S_ {n} ^ {w} - w_ {n + 1} S_n ^ {wx}} {S_ {n + 1} ^ {w} S_ {n} ^ {w}} = \ frac {w_ {n + 1} x_ {n +1} S_n ^ w - w_ {n + 1} S_n ^ {wx}} {S_ {n + 1} ^ {w} S_ {n} ^ {w}}$$

$$

$$= \ frac {w_ {n + 1}} {S_ {n + 1} ^ {w}} \ Big (x_ {n + 1} - \ frac {S_n ^ {wx}} {S_n ^ w} \ Big ) = \ frac {w_ {n + 1}} {S_ {n + 1} ^ {w}} (x_ {n + 1} - m_n ^ {wx})$$

In particular, if all weights are equal to one, we get that

$$

$$m_ {n + 1} ^ {wx} = m_ {n} ^ {wx} + \ frac {x_ {n + 1} - m_n ^ {wx}} {n + 1}$$

By the way, formulas for the "weighted" case make it easy to implement operations that are different from adding exactly one successive number. For example, deleting the number $$$x$ out of the set for which the average is calculated is the same as adding a number $$$-x$ with weight $$$-1$ . Adding several numbers at once is the same as adding one of the average with a weight equal to the number of these numbers, and so on.

4. Calculation of covariances

We show that the classical formula for calculating the covariance is true for the weighted problem. For simplicity, we will now work with unrated values.

$$

$$D_ {n} ^ {wxy} = \ sum_ {i = 1} ^ {n} w_i (x_i - m_n ^ {wx}) (y_i - m_n ^ {wy}) = S_n ^ {wxy} - m_n ^ { wx} S_n ^ {wy} - S_n ^ {wx} m_n ^ {wy} + S_n ^ wm_n ^ {wx} m_n ^ {wy}$$

From here it is easy to see that

$$

$$D_ {n} ^ {wxy} = S_n ^ {wxy} - \ frac {S_n ^ {wx} S_n ^ {wy}} {S_n ^ w}$$

This formula is extremely convenient, including for the online algorithm, however, if the values $$$S_n ^ {wxy}$ and $$${S_n ^ {wx} S_n ^ {wy}} / {S_n ^ w}$ will be close and at the same time large in absolute value, its use will lead to significant computational errors.

Let's try to derive a recurrent formula for $$$D_n ^ {wxy}$ , in a sense, a similar formula of Welford for the medium. So:

$$

$$D_ {n + 1} ^ {wxy} = S_n ^ {wxy} + w_ {n + 1} x_ {n + 1} y_ {n + 1} - w_ {n + 1} x_ {n + 1} \ frac {S_ {n + 1} ^ {wy}} {S_ {n + 1} ^ {w}} - \ frac {S_n ^ {wx} S_ {n + 1} ^ {wy}} {S_ {n + 1} ^ w} =$$

$$

$$= S_n ^ {wxy} + w_ {n + 1} x_ {n + 1} (y_ {n + 1} - m_ {n + 1} ^ {wy}) - \ frac {S_n ^ {wx} S_ { n + 1} ^ {wy}} {S_ {n + 1} ^ w}$$

Consider the last term:

$$

$$\ frac {S_n ^ {wx} S_ {n + 1} ^ {wy}} {S_ {n + 1} ^ w} = \ Big (\ frac {1} {S_n ^ w} - \ frac {w_ { n + 1}} {S_n ^ wS_ {n + 1} ^ w} \ Big) S_n ^ {wx} S_ {n + 1} ^ {wy} = \ frac {S_n ^ {wx} S_ {n + 1} ^ {wy}} {S_n ^ w} -w_ {n + 1} m_n ^ {wx} m_ {n + 1} ^ {wy} =$$

$$

$$= \ frac {S_n ^ {wx} S_ {n} ^ {wy}} {S_n ^ w} + w_ {n + 1} y_ {n + 1} \ frac {S_n ^ {wx}} {S_n ^ w } -w_ {n + 1} m_n ^ {wx} m_ {n + 1} ^ {wy} = \ frac {S_n ^ {wx} S_ {n} ^ {wy}} {S_n ^ w} + w_ {n +1} m_n ^ {wx} \ cdot (y_ {n + 1} -m_ {n + 1} ^ {wy})$$

Substitute the resulting expression for $$$D_ {n + 1} ^ {wxy}$ :

$$

$$D_ {n + 1} ^ {wxy} = S_n ^ {wxy} + w_ {n + 1} x_ {n + 1} (y_ {n + 1} - m_ {n + 1} ^ {wy}) - \ frac {S_n ^ {wx} S_ {n} ^ {wy}} {S_n ^ w} -w_ {n + 1} m_n ^ {wx} \ cdot (y_ {n + 1} -m_ {n + 1} ^ {wy}) =$$

$$

$$= \ Big [S_n ^ {wxy} - \ frac {S_n ^ {wx} S_ {n} ^ {wy}} {S_n ^ w} \ Big] + w_ {n + 1} (x_ {n + 1} -m_n ^ {wx}) (y_ {n + 1} - m_ {n + 1} ^ {wy}) =$$

$$

$$= D_ {n} ^ {wxy} + w_ {n + 1} (x_ {n + 1} -m_n ^ {wx}) (y_ {n + 1} - m_ {n + 1} ^ {wy})$$

The code that implements the calculations using this formula, in the absence of weights, looks very simple. It is necessary to update two average values, and also the sum of works:

 double WelfordCovariation(const std::vector<double>& x, const std::vector<double>& y) { double sumProducts = 0.; double xMean = 0.; double yMean = 0.; for (size_t i = 0; i < x.size(); ++i) { xMean += (x[i] - xMean) / (i + 1); sumProducts += (x[i] - xMean) * (y[i] - yMean); yMean += (y[i] - yMean) / (i + 1); } return sumProducts / x.size(); } 

Also interesting is the question of updating the value of the actual covariance, i.e. normalized value:

$$

$$C_ {n + 1} ^ {wxy} = \ frac {\ sum_ {i = 1} ^ {n + 1} w_i (x_i - m_ {n + 1} ^ {wx}) (y_i - m_ {n + 1} ^ {wy})} {\ sum_ {i = 1} ^ {n + 1} w_ {i}} = \ frac {D_ {n + 1} ^ {wxy}} {S_ {n + 1} ^ w} =$$

$$

$$= \ frac {1} {S_ {n + 1} ^ w} \ cdot \ Big (D_n ^ {wxy} + w_ {n + 1} (x_ {n + 1} -m_n ^ {wx})) (y_ {n + 1} - m_ {n + 1} ^ {wy}) \ Big) =$$

$$

$$= \ frac {D_n ^ {wxy}} {S_ {n + 1} ^ w} + \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} (x_ {n + 1} - m_n ^ {wx}) (y_ {n + 1} - m_ {n + 1} ^ {wy})$$

Consider the first term:

$$

$$\ frac {D_n ^ {wxy}} {S_ {n + 1} ^ w} = \ Big (\ frac {1} {S_n ^ w} - \ frac {w_ {n + 1}} {S_ {n + 1} ^ wS_n ^ w} \ Big) D_n ^ {wxy} = \ frac {D_n ^ {wxy}} {S_n ^ w} \ Big (1 - \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} \ Big) = C_n ^ {wxy} \ Big (1- \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} \ Big)$$

Back now to the review $$$C_ {n + 1} ^ {wxy}$ :

$$

$$C_ {n + 1} ^ {wxy} = C_n ^ {wxy} \ Big (1- \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} \ Big) + \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} (x_ {n + 1} -m_n ^ {wx}) (y_ {n + 1} - m_ {n + 1} ^ {wy})$$

This can be rewritten, for example, as follows:

$$

$$C_ {n + 1} ^ {wxy} = C_n ^ {wxy} + \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} \ Big ((x_ {n + 1} -m_n ^ {wx}) (y_ {n + 1} - m_ {n + 1} ^ {wy}) - C_n ^ {wxy} \ Big)$$

It turned out a formula that really has an amazing similarity with the formula for updating the average!

5. Experimental comparison of methods

I wrote a small program that implements three ways to calculate the covariance:

1. "Standard" algorithm that directly calculates values $$$S_n ^ {wxy}$ , $$$S_n ^ {wx}$ and $$$S_n ^ {wy}$ .
2. Algorithm using the Kahan method.
3. Algorithm using the method of Welford.

The data in the task are formed as follows: two numbers are selected, $$$m_x$ and $$$m_y$ - average of two samples. Then two more numbers are selected, $$$d_x$ and $$$d_y$ - accordingly, deviations. The input algorithms are given a sequence of numbers of the form

$$

$$x_i = m_x \ pm d_x,$$

$$

$$y_i = m_y \ pm d_y,$$

moreover, the signs of deviations change at each iteration, so that the true covariance is calculated as follows:

$$

$$C_ {n} ^ {xy} = \ frac {\ sum_ {i = 1} ^ {n} (x_i - m_x) (y_i - m_y)} {n} = d_x \ cdot d_y$$

The true covariance is constant and does not depend on the number of terms, so we can calculate the relative error of calculation for each method at each iteration. So, in the current implementation $$$d_x = d_y = 1$ , and averages take values ​​of 100000 and 1000000.

The first graph shows the dependence of the relative error when using the naive method for an average of 100 thousand. This graph demonstrates the inconsistency of the naive method: starting from a certain moment, the error begins to grow rapidly, reaching completely unacceptable values. On the same data methods Kahana and Welford do not allow significant errors.

The second graph is constructed for the Kahan method with an average of one million. The error does not grow with an increase in the number of terms, but although it is significantly lower than the error of the "naive" method, it is still too large for practical applications.

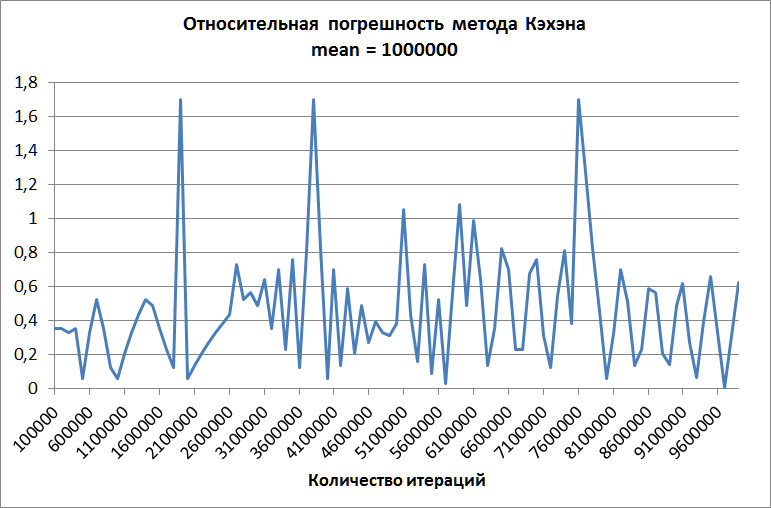
Welford's method, in turn, and on this data demonstrates perfect accuracy!

Conclusion

In this article, we compared several ways to calculate the covariance and made sure that the Welford method gives the best results. In order to use it in practice, it suffices to remember only the following two implementations:

 class TWelfordMeanCalculator { private: double Mean = 0.; size_t Count = 0; public: void Add(const float value) { ++Count; Mean += (value - Mean) / Count; } double GetMean() const { return Mean; } }; class TWelfordCovariationCalculator { private: size_t Count = 0; double MeanX = 0.; double MeanY = 0.; double SumProducts = 0.; public: void Add(const double x, const double y) { ++Count; MeanX += (x - MeanX) / Count; SumProducts += (x - MeanX) * (y - MeanY); MeanY += (y - MeanY) / Count; } double Covariation() const { return SumProducts / Count; } }; 

The use of these methods can save a lot of time and effort in situations where the data is arranged rather "unsuccessfully." You may encounter problems with the accuracy of calculations in arbitrarily unexpected situations, even with the implementation of the one-dimensional kMeans algorithm.

In the next article, we will consider the application of the considered methods in the problem of restoring linear regression, let's talk about the speed of calculations and how the common implementations of machine learning methods deal with "bad" data.

Literature

1. github.com: Different covariation calculation methods
2. machinelearning.ru: The addition of a large set of numbers that differ significantly in size
3. ru.wikipedia.org: Kahan Algorithm
4. en.wikipedia.org: Algorithms for calculating variance: Online algorithm