Reverse engineering one line javascript
A few months ago I received a letter from a friend:
Subject: Can you explain this one line of code to me?
Text: Consider me stupid, but ... I do not understand her and I will be grateful if you explain in detail. This is a ray tracer in 128 characters. I think he's amazing.
')
This line of JavaScript will draw the animation that is shown in the image below the cut. In the browser, it runs here . The script is written by the author www.p01.org , where you can find this and many other cool demos.

Challenge accepted!
The first thing I did was leave HTML in HTML, the JavaScript code was transferred to the
index.html
I noticed that the variable
code.js
Further,
I also noticed that the
Then I declared the variables
I decomposed the
Here I have expanded the ternary operator
This value (index) is used to shift the string P, so we call it
I decomposed
Here is a clever way to check whether the result is even in parentheses, when 0 is returned for an even value, and 1. is returned for an odd value.
Consequently,
In other words, the five is an odd number, and the result of 5 AND 1 (5 & 1) will be 1. In the JavaScript console, it is easy to verify that this logic is adhered to.
Note that I also renamed the rest of the
Next, I deployed
I dealt with the operator
I also renamed
And last but not least, I put the parentheses in
Clarification: I was told that I mistakenly placed
The final result of the execution can be seen here .
So what's going on here? Let's figure it out.
Initially, the value of
The image consists of 32 lines, with 128 characters each. It is very convenient that 64 × 64 = 32 × 128 = 4096. The value of
But when to install
Well, for a start we know exactly what should be installed
But when
If you remove

Now look at
Pay attention to what happens in each cycle:
In other words, we can express
In this case, we can rewrite
We use an online graphing calculator to draw graphs of some of these functions.
First of all, draw
There is a nice graph with y values from 0 to 2.

If we draw

If you draw the entire left side of the expression, you get a graph that looks like a combination of the previous two.

In the end, if we draw two functions next to each other, we will see the following.

Let's recall the question we are trying to answer, that is, how did such a beautiful static picture come up:

We know that if “magic”
Increase the first 16 lines of our graph, where
The bitwise XOR in JavaScript will drop all values to the right of the comma, so this is equivalent to applying the
It will return 0 if both bits are 1 or both are 0.
Our
In other words, each green diagonal represents one row in our graph. Since for the first 16 rows the value of j is always greater than 1, but less than 2, we can get an odd value only if the left side of the expression
Here are some results from the JavaScript console to see the results of the calculations: 0 or −2 means that the result is even, and 1 means an odd number.
If you look at our graph, then there the rightmost diagonal line barely goes above 1 and below −1 (few even numbers — few

After the 16th row, the value of
If you look at the few bottom lines in the animated picture, you will notice that they do not follow the same pattern due to the large fluctuation of the graph.
Now back to
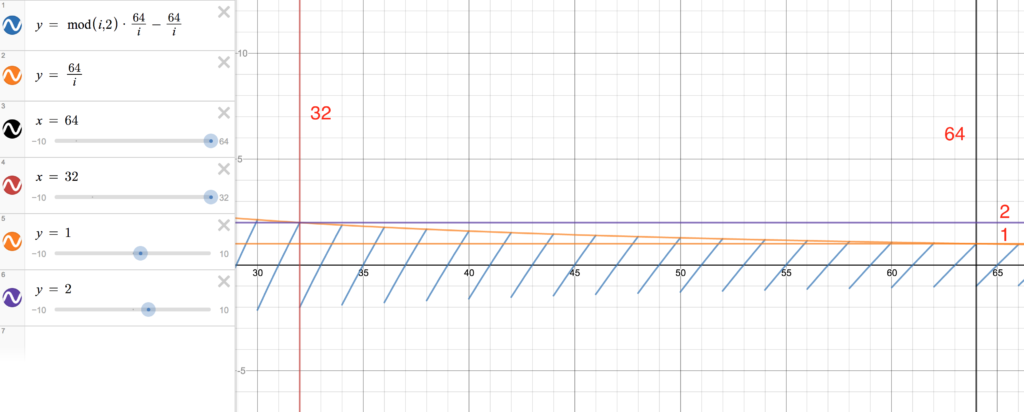
After reaching the value of 64, the graph changes as follows.

Notice that
HTML rendering for such a condition looks like this (you can hard-drive the value of

By this time, the number of characters
For example, when

Please note that the diagonal for the first row (near the 64 mark) has moved approximately one small square up. Since the four large squares are 128 characters, there will be 32 characters in one large square, and 32/5 = 6.4 characters (approximately) in one small square. If we look at rendering HTML, then there the first row really moved to the right by 7 characters.

And one last example. This is what happens if you call setInterval seven more times, and

For the first row,
It will look like this.

The schedule is endlessly looped.
I hope our work has some meaning. It is unlikely that I would ever be able to come up with something similar on my own, but it was interesting to understand this code.
Subject: Can you explain this one line of code to me?
Text: Consider me stupid, but ... I do not understand her and I will be grateful if you explain in detail. This is a ray tracer in 128 characters. I think he's amazing.
')
<pre id=p><script>n=setInterval("for(n+=7,i=k,P='p.\\n';i-=1/k;P+=P[i%2?(i%2*j-j+n/k^j)&1:2])j=k/i;p.innerHTML=P",k=64)</script> This line of JavaScript will draw the animation that is shown in the image below the cut. In the browser, it runs here . The script is written by the author www.p01.org , where you can find this and many other cool demos.

Challenge accepted!
Part I. Extract the readable code.
The first thing I did was leave HTML in HTML, the JavaScript code was transferred to the
code.js file, and p quoted in id="p" .index.html
<script src="code.js"></script> <pre id="p"></pre> I noticed that the variable
k is just a constant, so I removed it from the line and renamed delay .code.js
var delay = 64; var draw = "for(n+=7,i=delay,P='p.\\n';i-=1/delay;P+=P[i%2?(i%2*j-j+n/delay^j)&1:2])j=delay/i;p.innerHTML=P"; var n = setInterval(draw, delay); Further,
var draw was just a string that was executed as a function of eval at intervals of setInterval, because setInterval can take both functions and strings. I moved var draw to an explicit function, but I saved the original line for reference just in case.I also noticed that the
p element actually referred to the DOM element with the p identifier declared in HTML, which I recently quoted. It turns out that elements in JavaScript can be referenced by their identifier, if id consists only of letters and numbers. I added document.getElementById("p") to make the code clearer. var delay = 64; var p = document.getElementById("p"); // < -------------- // var draw = "for(n+=7,i=delay,P='p.\\n';i-=1/delay;P+=P[i%2?(i%2*j-j+n/delay^j)&1:2])j=delay/i;p.innerHTML=P"; var draw = function() { for (n += 7, i = delay, P = 'p.\n'; i -= 1 / delay; P += P[i % 2 ? (i % 2 * j - j + n / delay ^ j) & 1 : 2]) { j = delay / i; p.innerHTML = P; } }; var n = setInterval(draw, delay); Then I declared the variables
i , p and j and transferred them to the beginning of the function. var delay = 64; var p = document.getElementById("p"); // var draw = "for(n+=7,i=delay,P='p.\\n';i-=1/delay;P+=P[i%2?(i%2*j-j+n/delay^j)&1:2])j=delay/i;p.innerHTML=P"; var draw = function() { var i = delay; // < --------------- var P ='p.\n'; var j; for (n += 7; i > 0 ;P += P[i % 2 ? (i % 2 * j - j + n / delay ^ j) & 1 : 2]) { j = delay / i; p.innerHTML = P; i -= 1 / delay; } }; var n = setInterval(draw, delay); I decomposed the
for loop and converted it into a while . Of the three parts of the former for , only one part of the CHECK_EVERY_LOOP remained, and the rest (RUNS_ONCE_ON_INIT; DO_EVERY_LOOP) moved beyond the cycle. var delay = 64; var p = document.getElementById("p"); // var draw = "for(n+=7,i=delay,P='p.\\n';i-=1/delay;P+=P[i%2?(i%2*j-j+n/delay^j)&1:2])j=delay/i;p.innerHTML=P"; var draw = function() { var i = delay; var P ='p.\n'; var j; n += 7; while (i > 0) { // <---------------------- //Update HTML p.innerHTML = P; j = delay / i; i -= 1 / delay; P += P[i % 2 ? (i % 2 * j - j + n / delay ^ j) & 1 : 2]; } }; var n = setInterval(draw, delay); Here I have expanded the ternary operator
( condition ? do if true : do if false) in P += P[i % 2 ? (i % 2 * j - j + n / delay ^ j) & 1 : 2]; ( condition ? do if true : do if false) in P += P[i % 2 ? (i % 2 * j - j + n / delay ^ j) & 1 : 2]; .i%2 checks if the variable i even or odd. If it is even, then it simply returns 2. If it is odd, then it returns the magic value magic (i % 2 * j - j + n / delay ^ j) & 1; (more on this later).This value (index) is used to shift the string P, so we call it
index and turn the string into P += P[index]; . var delay = 64; var p = document.getElementById("p"); // var draw = "for(n+=7,i=delay,P='p.\\n';i-=1/delay;P+=P[i%2?(i%2*j-j+n/delay^j)&1:2])j=delay/i;p.innerHTML=P"; var draw = function() { var i = delay; var P ='p.\n'; var j; n += 7; while (i > 0) { //Update HTML p.innerHTML = P; j = delay / i; i -= 1 / delay; let index; let iIsOdd = (i % 2 != 0); // <--------------- if (iIsOdd) { // <--------------- index = (i % 2 * j - j + n / delay ^ j) & 1; } else { index = 2; } P += P[index]; } }; var n = setInterval(draw, delay); I decomposed
& 1 from the value index = (i % 2 * j - j + n / delay ^ j) & 1 into another if .Here is a clever way to check whether the result is even in parentheses, when 0 is returned for an even value, and 1. is returned for an odd value.
& is a bitwise AND operator. It works like this:- 1 & 1 = 1
- 0 & 1 = 0
Consequently,
something & 1 converts the "something" into a binary representation, and also finishes the required number of zeros before the unit to match the size of the "something", and returns just the AND result of the last bit. For example, 5 in binary format equals 101 , so if we apply the logical AND operation with a unit on it, we get the following: 101 AND 001 001 In other words, the five is an odd number, and the result of 5 AND 1 (5 & 1) will be 1. In the JavaScript console, it is easy to verify that this logic is adhered to.
0 & 1 // 0 - even return 0 1 & 1 // 1 - odd return 1 2 & 1 // 0 - even return 0 3 & 1 // 1 - odd return 1 4 & 1 // 0 - even return 0 5 & 1 // 1 - odd return 1 Note that I also renamed the rest of the
index to magic , so the code with the expanded &1 will look like this: var delay = 64; var p = document.getElementById("p"); // var draw = "for(n+=7,i=delay,P='p.\\n';i-=1/delay;P+=P[i%2?(i%2*j-j+n/delay^j)&1:2])j=delay/i;p.innerHTML=P"; var draw = function() { var i = delay; var P ='p.\n'; var j; n += 7; while (i > 0) { //Update HTML p.innerHTML = P; j = delay / i; i -= 1 / delay; let index; let iIsOdd = (i % 2 != 0); if (iIsOdd) { let magic = (i % 2 * j - j + n / delay ^ j); let magicIsOdd = (magic % 2 != 0); // &1 < -------------------------- if (magicIsOdd) { // &1 <-------------------------- index = 1; } else { index = 0; } } else { index = 2; } P += P[index]; } }; var n = setInterval(draw, delay); Next, I deployed
P += P[index]; in the switch . At this point, it became clear that index can take only one of three values — 0, 1, or 2. It is also clear that the variable P always initialized with the values var P ='p.\n'; where 0 points to p , 1 points to . , and 2 points to a \n newline character var delay = 64; var p = document.getElementById("p"); // var draw = "for(n+=7,i=delay,P='p.\\n';i-=1/delay;P+=P[i%2?(i%2*j-j+n/delay^j)&1:2])j=delay/i;p.innerHTML=P"; var draw = function() { var i = delay; var P ='p.\n'; var j; n += 7; while (i > 0) { //Update HTML p.innerHTML = P; j = delay / i; i -= 1 / delay; let index; let iIsOdd = (i % 2 != 0); if (iIsOdd) { let magic = (i % 2 * j - j + n / delay ^ j); let magicIsOdd = (magic % 2 != 0); // &1 if (magicIsOdd) { // &1 index = 1; } else { index = 0; } } else { index = 2; } switch (index) { // P += P[index]; <----------------------- case 0: P += "p"; // aka P[0] break; case 1: P += "."; // aka P[1] break; case 2: P += "\n"; // aka P[2] } } }; var n = setInterval(draw, delay); I dealt with the operator
var n = setInterval(draw, delay); . The setInterval method returns integers starting from one, increasing the value with each call. This integer can be used for clearInterval (that is, for undo). In our case, setInterval is called only once, and the variable n simply set to 1.I also renamed
delay to DELAY to remind you that this is just a constant.And last but not least, I put the parentheses in
i % 2 * j - j + n / DELAY ^ j to indicate that y ^ (bitwise XOR) is lower priority than the % , * , − , + and / . In other words, all the above calculations will be performed first, and only then ^ . That is, it turns out (i % 2 * j - j + n / DELAY) ^ j) .Clarification: I was told that I mistakenly placed
p.innerHTML = P; //Update HTML p.innerHTML = P; //Update HTML into a loop, so I removed it from there. const DELAY = 64; // approximately 15 frames per second 15 frames per second * 64 seconds = 960 frames var n = 1; var p = document.getElementById("p"); // var draw = "for(n+=7,i=delay,P='p.\\n';i-=1/delay;P+=P[i%2?(i%2*j-j+n/delay^j)&1:2])j=delay/i;p.innerHTML=P"; /** * Draws a picture * 128 chars by 32 chars = total 4096 chars */ var draw = function() { var i = DELAY; // 64 var P ='p.\n'; // First line, reference for chars to use var j; n += 7; while (i > 0) { j = DELAY / i; i -= 1 / DELAY; let index; let iIsOdd = (i % 2 != 0); if (iIsOdd) { let magic = ((i % 2 * j - j + n / DELAY) ^ j); // < ------------------ let magicIsOdd = (magic % 2 != 0); // &1 if (magicIsOdd) { // &1 index = 1; } else { index = 0; } } else { index = 2; } switch (index) { // P += P[index]; case 0: P += "p"; // aka P[0] break; case 1: P += "."; // aka P[1] break; case 2: P += "\n"; // aka P[2] } } //Update HTML p.innerHTML = P; }; setInterval(draw, 64); The final result of the execution can be seen here .
Part 2. Understanding the code
So what's going on here? Let's figure it out.
Initially, the value of
i set to 64 by means of var i = DELAY; and then each cycle it decreases by 1/64 (0.016625) through i -= 1 / DELAY; . The loop continues until i greater than zero ( while (i > 0) { code while (i > 0) { ). Since for each pass i decreases by 1/64, it takes 64 cycles before it decreases by one (64/64 = 1). In general, a decrease in i will occur 64 × 64 = 4096 times in order to decrease to zero.The image consists of 32 lines, with 128 characters each. It is very convenient that 64 × 64 = 32 × 128 = 4096. The value of
i can be even (not odd let iIsOdd = (i % 2 != 0); ) if i is strictly an even number. This will happen 32 times when it equals 64, 62, 60, etc. These 32 times the index will take the value 2 index = 2; , and a new line character will be added to the line: P += "\n"; // aka P[2] P += "\n"; // aka P[2] . The remaining 127 characters in the string will take the values p or . .But when to install
p , and when . ?Well, for a start we know exactly what should be installed
. for odd values, let magic = ((i % 2 * j - j + n / DELAY) ^ j); , or set p if "magic" is even. var P ='p.\n'; ... if (magicIsOdd) { // &1 index = 1; // second char in P - . } else { index = 0; // first char in P - p } But when
magic even and when is odd? This is a million dollar question. Before moving on to it, let's define something else.If you remove
+ n/DELAY from let magic = ((i % 2 * j - j + n / DELAY) ^ j); , you get a static picture in which nothing moves at all:
Now look at
magic without + n/DELAY . How did this beautiful picture come about?(i % 2 * j - j) ^ jPay attention to what happens in each cycle:
j = DELAY / i; i -= 1 / DELAY; In other words, we can express
j through finite i as j = DELAY/ (i + 1/DELAY) . But since 1 / DELAY is too small a number, for this example you can drop + 1/DELAY and simplify the expression to j = DELAY/i = 64/i .In this case, we can rewrite
(i % 2 * j - j) ^ j as i % 2 * 64/i - 64/i) ^ 64/i .We use an online graphing calculator to draw graphs of some of these functions.
First of all, draw
i%2 .There is a nice graph with y values from 0 to 2.

If we draw
64/i , we get the following graph:
If you draw the entire left side of the expression, you get a graph that looks like a combination of the previous two.

In the end, if we draw two functions next to each other, we will see the following.

What do these charts say?
Let's recall the question we are trying to answer, that is, how did such a beautiful static picture come up:

We know that if “magic”
(i % 2 * j - j) ^ j takes an even value, then you need to add p , and for an odd number you need to add . .Increase the first 16 lines of our graph, where
i has values from 64 to 32.
The bitwise XOR in JavaScript will drop all values to the right of the comma, so this is equivalent to applying the
Math.floor method, which rounds the number down.It will return 0 if both bits are 1 or both are 0.
Our
j starts from one and slowly moves to a two, stopping right next to it, so we can always consider it as a unit when rounding down ( Math.floor(1.9999) === 1 ), and we need one more unit on the left side to get a result of zero and give us p .In other words, each green diagonal represents one row in our graph. Since for the first 16 rows the value of j is always greater than 1, but less than 2, we can get an odd value only if the left side of the expression
(i % 2 * j - j) ^ j , it is i % 2 * i/64 — i/64 , that is, the green diagonal, will also be higher than 1 or lower than −1.Here are some results from the JavaScript console to see the results of the calculations: 0 or −2 means that the result is even, and 1 means an odd number.
1 ^ 1 // 0 - even p 1.1 ^ 1.1 // 0 - even p 0.9 ^ 1 // 1 - odd . 0 ^ 1 // 1 - odd . -1 ^ 1 // -2 - even p -1.1 ^ 1.1 // -2 - even p If you look at our graph, then there the rightmost diagonal line barely goes above 1 and below −1 (few even numbers — few
p characters). The next one goes a little further beyond these boundaries, the third one goes a little further, and so on. Line number 16 is barely held between 2 and −2. After line 16, we see that our static graph changes its character.
After the 16th row, the value of
j crosses the limit 2, so that the expected result changes. Now we will get an even number if the green diagonal line is higher than 2 or lower than −2, or inside frames 1 and −1, but does not touch them. That is why we see in the picture two or more groups of p characters starting from the 17th line.If you look at the few bottom lines in the animated picture, you will notice that they do not follow the same pattern due to the large fluctuation of the graph.
Now back to
+ n/DELAY . In the code, we see that the value of n begins with 8 (1 from setInteval and plus 7 on each method call). It then increases by 7 each time setInteval is triggered.After reaching the value of 64, the graph changes as follows.

Notice that
j is still around one, but now the left half of the red diagonal is around 62-63, around about zero, and the right half is around 63-64 around one. Since our characters appear in descending order from 64 to 62, we can expect that the right half of the diagonal in the region of 63-64 (1 ^ 1 = 0 // even) will add a handful of characters p , and the left half of the diagonal in the region of 62-63 ( 1 ^ 0 = 1 // odd) will add a bunch of points. All this will grow from left to right, as usual text.HTML rendering for such a condition looks like this (you can hard-drive the value of
n in the CodePen editor and see). This coincides with our expectations.
By this time, the number of characters
p has grown to a constant value. For example, in the first row, half of all values will always be even. Now the characters p and . will only change places.For example, when
n incremented by 7 on the next call to setInterval, the graph changes slightly.
Please note that the diagonal for the first row (near the 64 mark) has moved approximately one small square up. Since the four large squares are 128 characters, there will be 32 characters in one large square, and 32/5 = 6.4 characters (approximately) in one small square. If we look at rendering HTML, then there the first row really moved to the right by 7 characters.

And one last example. This is what happens if you call setInterval seven more times, and
n equals 64 + 9 × 7.
For the first row,
j is still equal to 1. Now the upper half of the red diagonal near the 64 mark abutted approximately into two, and the lower end near the unit. This turns the picture in the other direction, since now 1^2 = 3 // odd - . and 1 ^ 1 = 0 //even - p . So you can expect a bunch of points, followed by the characters p .It will look like this.

The schedule is endlessly looped.
I hope our work has some meaning. It is unlikely that I would ever be able to come up with something similar on my own, but it was interesting to understand this code.
Source: https://habr.com/ru/post/333372/
All Articles