Historical essay on the great mathematician Karl Friedrich Gauss

Karl Friedrich Gauss

Mathematician and historian of mathematics Jeremy Gray tells Gauss and his enormous contribution to science, about the theory of quadratic forms, the discovery of Ceres, and non-Euclidean geometry *

Portrait of Gauss Edward Riethmüller on the terrace of the Göttingen Observatory // Karl Friedrich Gauss: Titan of Science G. Waldo Dunnington, Jeremy Gray, Fritz-Egbert Doha

Karl Friedrich Gauss was a German mathematician and astronomer. He was born to poor parents in Braunschweig in 1777 and died in Göttingen in Germany in 1855, and by that time everyone who knew him considered him one of the greatest mathematicians of all time.

Gauss Study

How do we study Carl Friedrich Gauss? Well, when it comes to his early life, we have to rely on family stories that his mother shared when he became famous. Of course, these stories are prone to exaggeration, but his remarkable talent was noticeable, already when Gauss was in his early teens. Since then, we have more and more records about his life.
When Gauss grew up and became noticed, we began to receive letters about him about people who knew him, as well as official reports of various kinds. We also have a long biography of his friend, written on the basis of the conversations they had at the end of Gauss's life. We have his publications, we have a lot of his letters to other people, and he wrote a lot of material, but he never published it. And finally, we have obituaries.

Early life and the path to mathematics

Gauss's father was engaged in various affairs, was a worker, a master of the construction site and a merchant assistant. His mother was intelligent, but barely literate, and devoted herself completely to Gauss until her death at the age of 97 years. It seems that Gauss was seen as a gifted student still at school, at eleven years old, his father was persuaded to send him to a local academic school, instead of forcing him to work. At that time, the Duke of Brunswick sought to modernize his duchy, and attracted talented people to help him. When Gauss turned fifteen, the duke brought him to the college of Karolinum for his higher education, although by that time Gauss had already independently studied Latin and mathematics at the higher school level. At the age of eighteen, he entered the University of Göttingen, and at twenty-one had already written his doctoral dissertation.

Initially, Gauss was going to study philology, a priority subject in Germany at that time, but he also conducted extensive research on the algebraic construction of regular polygons. Due to the fact that the vertices of a regular polygon of N sides are given by solving the equation $$$x ^ {(n - 1)} = 0$(which is numerically equal to $$$e ^ {(2ki \ pi / 17)} = cos (2k \ pi / 17) + i sin (2k \ pi / 17), k = 0, 1,. . . 16)$. Gauss found that when n = 17, the equation is factorized in such a way that a regular 17-sided polygon can be constructed only along a ruler and compass. It was a completely new result, the Greek geometers were unaware of this, and the discovery caused a slight sensation - news of this was even published in the city newspaper. This success, which came when he was barely nineteen, made him decide to study mathematics.

But what made him famous was two completely different phenomena in 1801. The first was the publication of his book entitled Arithmetic Reasoning, which completely rewrote number theory and led to the fact that it (number theory) has become, and is still, one of the central subjects of mathematics. It includes a theory of equations of the form x ^ n - 1, which is at the same time a very original and at the same time easily perceptible, as well as a much more complex theory, called the theory of a quadratic form. This has already attracted the attention of two leading French mathematicians, Joseph Louis Lagrange and Adrienne Marie Legendre, who admitted that Gauss went very far beyond all that they were doing.

The second important event was the reopening of the first known asteroid by Gauss. It was found in 1800 by the Italian astronomer Giuseppe Piazzi, who named him Ceres in honor of the Roman goddess of agriculture. He watched her for 41 nights before she disappeared behind the sun. It was a very exciting discovery, and astronomers really wanted to know where it would appear again. Only Gauss calculated it correctly, which none of the professionals did, and this made his name as an astronomer, which he remained for many years to come.

Late life and family

Gauss's first work was a mathematician in Göttingen, but after the discovery of Ceres, and then other asteroids, he gradually switched his interests to astronomy, and in 1815 became the director of the Göttingen Observatory, and held this position until his death. He also remained a professor of mathematics at the University of Göttingen, but this did not seem to require much teaching from him, and the records of his contacts with the younger generations were rather insignificant. In fact, he seems to have been an alienated figure, more comfortable and sociable with astronomers, and few good mathematicians in his life.

In the 1820s, he led a massive study of northern Germany and southern Denmark, and in the course of this he rewrote the theory of surface geometry or differential geometry, as it is called today.

Gauss married twice, for the first time quite happily, but when his wife Joanna died during childbirth in 1809, he again married Minna Waldeck, but this marriage was less successful; She died in 1831. He had three sons, two of whom emigrated to the United States, most likely because their relationship with their father was problematic. As a result, there is an active group of people in the States who originate from Gauss. He also had two daughters, one from each marriage.

Greatest contribution to mathematics

Considering the Gauss contribution in this area, we can start with the least squares method in statistics that he invented in order to understand the Piazzi data and find the asteroid Ceres. It was a breakthrough in averaging a large number of observations, all of which were slightly inaccurate in order to get the most reliable information from them. As for the theory of numbers, it can be talked about for a very long time, but he made remarkable discoveries about which numbers can be expressed in quadratic forms, which are expressions of the form $$$3x ^ 2 + 5xy + 6y ^ 2$. It may seem to you that this is important, but Gauss turned what was a collection of disparate results into a systematic theory, and showed that many simple and natural hypotheses have proofs that look like other branches of mathematics in general. Some of the techniques he invented turned out to be important in other areas of mathematics, but Gauss discovered them even before these branches were correctly studied: group theory is an example.

His work on the equations of the form $$$x ^ {(n - 1)} = 0$and, more surprisingly, by the deep features of the theory of quadratic forms, opened the use of complex numbers, for example, to prove the results on integers. This suggests that a lot was happening under the surface of the object.

Later, in the 1820s, he discovered that there is a concept of surface curvature, which is an integral part of the surface. This explains why some surfaces cannot be accurately copied to others, without transformations, as we cannot make an exact map of the Earth on a sheet of paper. This freed up the study of surfaces from the study of solids: you can have apple peel, without the need to imagine an apple under it.

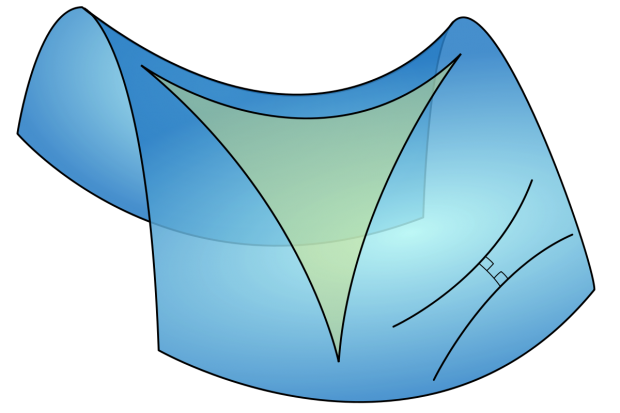
Surface with negative curvature, where the sum of the angles of the triangle is less than that of the triangle on the plane // source: Wikipedia

In the 1840s, regardless of the English mathematician George Green, he invented the subject of potential theory, which is a huge extension of the calculus of functions of several variables. This is the correct mathematics for the study of gravity and electromagnetism and has since been used in many fields of applied mathematics.

And we must also remember that Gauss discovered, but did not publish quite a lot. No one knows why he did so much for himself, but one theory is that the flow of new ideas that he had in his head was even more exciting. He assured himself that Euclid’s geometry is not necessarily true and that at least one other geometry is logically possible. Glory to this discovery went to two other mathematicians, Bolyai in Romania-Hungary and Lobachevsky in Russia, but only after their death — it was so controversial at the time. And he worked a lot on the so-called elliptic functions - you can consider them as generalizations of the sinusoidal and cosine functions of trigonometry, but, more precisely, they are complex functions of a complex variable, and Gauss invented a whole theory of them. Ten years later, Abel and Jacobi became famous for having done the same thing, not knowing that Gauss had already done it.

Work in other areas

After his re-discovery of the first asteroid, Gauss worked extensively on finding other asteroids and calculating their orbits. It was a difficult job in the pre-computer era, but he turned to his talents, and he seemed to feel that this work allowed him to pay his debt to the prince and the society that gave him education.

In addition, while shooting in northern Germany, he invented a heliotrope for accurate shooting, and in the 1840s he helped create and build the first electric telegraph. If he had also thought about amplifiers, he could have been noted in this, since without them the signals could not travel very far.

Durable Heritage

There are many reasons why Karl Friedrich Gauss is still so relevant today. First of all, the theory of numbers has become a huge subject with a very complex reputation. Since then, some of the best mathematicians to him, and Gauss gave them a way to get closer to him. Naturally, some problems that he could not solve attracted attention, so you can say that he created a whole field of research. It turns out that it also has deep connections with the theory of elliptic functions.

In addition, his discovery of the internal concept of curvature enriched the entire study of surfaces and inspired subsequent generations for many years of work. Anyone who studies surfaces, from adventurous modern architects to mathematicians, is indebted to him.

The internal geometry of the surfaces extends to the idea of ​​the internal geometry of objects of higher order, such as three-dimensional space and four-dimensional space-time.

Einstein’s general theory of relativity and all modern cosmology, including the study of black holes, were made possible by the fact that Gauss made this breakthrough. The idea of ​​non-Euclidean geometry, so shocked at one time, made people realize that there could be many types of strict mathematics, some of which may be more accurate or useful - or just interesting - than those we knew about.

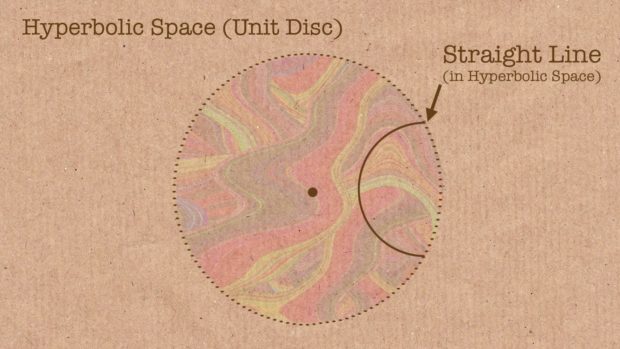
Non-Euclidean geometry // source: Numberphile

The man behind the legend

The life of Gauss has spawned many stories and anecdotes. For example, no matter how incredible, his mother loved to say that no one taught the basics of Gauss arithmetic, but he coped with it while listening to his father at work. Undoubtedly, he was one of the few mathematicians with an extraordinary ability for mental arithmetic and could quickly and accurately carry out long calculations in mind. It was also reported that his sons said that he discouraged them from pursuing a career in science, because "he did not want the name of Gauss to be associated with second-rate work."

In the same vein, he had a frightening habit of telling people that he already knew what they had just discovered. The most famous case, when his old university friend Farkas Boyai wrote to him, attaching a copy of his son Janos' discovery of non-Euclidean geometry, Gauss replied that he could not praise the work, saying “because doing so is the same as praising yourself.” This not only exaggerated what Gauss knew in 1831, he did not do anything to help the young Bolyi to gain recognition for his work, and Janosh was so disappointed that he never published it.

However, you should not get the impression that Gauss was an unpleasant person. He was a man of principle, he was happy to accept Sophie Germain as a serious mathematician at a time when women were excluded from higher education, and he always sought to use his talents for productive use. But his exceptional talents, and, although we can only rejoice over them, Radaktorververkhoditno, made him very lonely.

Jeremy Gray, doctor, honored pr.fessor of the history of mathematics, Open University.

→ Original article

* Inaccurate translation.