Post-quantum cryptography and the decline of the RSA - a real threat or an imaginary future?

RSA, elliptic curves, quantum computer, isogeny ... At first glance, these words resemble some spells, but everything is much more complicated than it seems!

The need to move to cryptography, resistant to an attack on a quantum computer, has already been officially announced by NIST and NSA , from which the conclusion is rather simple: it's time to get out of your comfort zone!

So, it is worthwhile to move away from the good old RSA and even, probably, from the elliptic curves that are beloved by many and learn new, equally interesting primitives that can protect confidential information.
')
To understand the intricacies of cryptography on elliptic curves, to trace the newfangled trends of post-quantum cryptography and even to touch it using the Microsoft SIDH library, welcome to the cat,%% username !

1. Let's start with the basics: a little bit about cryptography

What is cryptography and what is it for? Let's say Alice and Bob want to exchange a message, so much so that its content remains secret. Obviously, each side must have its own key. And at this stage, two subspecies of cryptosystems can be distinguished.

The first of these are symmetric cryptosystems. Here, one key can be easily computed from another, and often they coincide altogether. Significant advantages of such cryptosystems are the ease of implementation and high speed due to the use of simpler operations. However, if one of the keys is compromised, any attempt to protect sensitive information will lose its meaning.

Such a problem is elegantly solved in asymmetric cryptosystems using special algorithms. However, here we are faced with the laboriousness of operations, which may be inefficient for a large amount of data. In such cryptosystems, you need to really try to calculate another from one key, and, until someone’s computer has the enormous power of the dark side , you can be relatively calm about the secrecy of the data being protected.

An interesting mnogohodovochka ... Well, how will it be realized, ask inquisitive % username% ? It's all about the so-called one - way functions . Let there be a function $$$y = f (x)$ . By well-known argument $$$x$ calculate function value $$$y$ easier than to capture Westeros with three dragons and an army of flawless. However, the calculation of the argument $$$x$ by the known value of the function $$$y$ is quite a laborious task.

The most well-known candidates for one-sided functions are the problem of factoring a number, which consists in decomposing a number into simple factors, and the problem of discrete logarithmization, which consists in finding the unknown $$$k$ by known values $$$y$ and $$$g$ that satisfy: $$$y = g ^ k$ . The first, for example, is used in the well-known RSA cryptosystem, and the second can be found in the Diffie-Hellman key establishment scheme.

However, taking into account the rapid growth of the productivity of computing devices, like the flight of a dragon, there is a need to increase the key length, well, this can be a critical factor for devices with limited power ... Oh, it would be so great if such a structure appeared that would reduce the size key with the same level of resistance ... And, fortunately, it exists! The name of this miracle is an elliptic curve.

2. And now more difficult: elliptic curves.

If your face has taken a similar Harold expression, do not rush to close the article and run away, publishing a nervous laugh. Elliptic curves - it's easy! To begin, we give a definition. An elliptical curve is, first of all, a female non-singular cubic curve. It is called non-singular because a tangent can be uniquely drawn to all its points. Well, since this is a cubic curve, then it should be defined by a third-degree equation, which in the generalized Weierstrass form is as follows:

$$

$$y ^ 2 + a_1 xy + a_3y = x ^ 3 + a_2x ^ 2 + a_4x + a_6$$

However, in practice, this shape of the curve can be met infrequently. There are forms of Legendre, Montgomery , Hesse , etc. The use of one form or another can increase the efficiency of operations on points of an elliptic curve. For example, in the Montgomery form, it is possible to multiply a point by a number in a fixed time thanks to the Montgomery staircase algorithm.

Surely many were faced with the Weierstrass form, it is called canonical for fields with characteristic $$$char K \ neq 2,3$ :

$$

$$E (K): y ^ 2 = x ^ 3 + ax + b$$

An important characteristic of an elliptic curve is its discriminant , which for the Weierstrass form is calculated as follows: $$$\ Delta = 4a ^ 3 + 27b ^ 2$ .

The discriminant should not be zero , otherwise the curve will no longer be elliptical, since there will be inflection points, as on the curve $$$y ^ 2 = x ^ 3-3x + 2$ in the picture on the right.

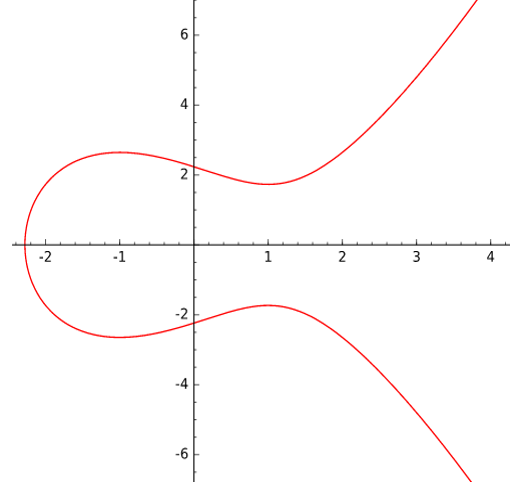
Surely, many people know the image of an elliptic curve, which can be seen in the figure on the left. Here is a view curve $$$y ^ 2 = x ^ 3-3x + 5$ given over the field of rational numbers.

However, when using rational numbers there is a difficulty with their rounding, and, as a result, with the ambiguity of the encryption and decryption operations. Therefore, in cryptography, elliptic curves are defined over a finite field , where the coordinates of the points are field elements. The curve of the curve, of course, will lose its former attractiveness, smooth lines will be replaced by points, but we love elliptic curves not for that!

It is necessary to mention one more characteristic of elliptic curves, which (SPOILER!) Still gives readers its presence in the article. This is about $$$j-$ invariant , constant value. His calculation for the Weierstrass elliptic curve also does not have a frightening effect on the body: $$$j = 1728 \ frac {4a ^ 3} {4a ^ 3 + 27b ^ 2}$

Group properties

An important point in cryptography on elliptic curves is that the points of an elliptic curve with an abstract point at infinity form an Abelian group . Let’s take addition as a group operation, then a group is an algebraic structure that has the following properties:

• Closure means that the result of the addition of the elements of a group is also an element of the group. We translate the terms of an elliptic curve: adding points of an elliptic curve results in a point belonging to the same curve.
  
  
  
  As can be seen from the figures above, the geometric meaning of the addition of points on an elliptic curve is as follows: it is necessary to cut through the folding points and reflect the intersection point of this straight line with the elliptic curve relative to the axis Ox.
• Associativity means the independence of the result of addition from changing the order of action.
  
• There must be a neutral element in the group. The result of adding any element of the group $$$g$ and neutral will be equal to the same element. In elliptic curves, the role of the neutral element is played by the infinitely distant point: $$$P_ \ infty: P_ \ infty + P = P + P_ \ infty = P$
  
  
• For each element there should be an inverse to it (relative to the main operation). With the addition of an element of a group and its reverse, we obtain a neutral element.
  
• The commutativity property is familiar to us from school mathematics: the sum does not change from the permutation of the terms. This property makes the group abelian.

A few words about persistence

Now let's talk a little about the strength of cryptosystems based on the discrete logarithm problem. Let be $$$G$ - a finite cyclic group , that is, each of its elements will be represented as a degree of a single element - a generator $$$g$ : $$$<g \> = G = \ {1, g ^ 2, g ^ 3, ..., g ^ {q-1} \}$ .

Depending on the group selection $$$G$ There are various methods for solving the discrete logarithm problem. So, to solve the problem of discrete logarithmization in a finite field, on the general non- happiness, there are not only universal algorithms (the Polig-Hellman method, $$$\ rho$ - Pollard's method, etc.), which have exponential complexity, but also special ones , which have subexponential complexity (decomposition base method, number field sieve method).

If as a generator group $$$G$ If we take a point of an elliptic curve, then the crypto-angles will have to be content with only universal algorithms. Therefore, cryptography on elliptic curves "pampers" users with a smaller key length.

However, not all elliptic curves can provide a high level of security in cryptographic protocols. The first danger is super singular curves . Their advantage is the ease of calculating the number of points, in contrast to non-supersingular curves. There are many factors by which it is possible to distinguish a super-singular curve from a non-supersingular curve, but in this article we will not focus on this.

These curves are vulnerable to MOV attack , which allows reducing the calculation of the discrete logarithm problem in a group of points of an elliptic curve over a field $$$\ mathbb {F} _q$ to the discrete logarithm problem in a finite field $$$\ mathbb {F_q ^ k}$ . Considering that the key length in cryptography on elliptic curves is less, and that for super-singular curves the value $$$k$ not great, the implementation of this attack is extremely successful for the attacker.

So what's the problem? Use suitable elliptic curves and enjoy life! But it was not there…

3. Quantum threat

Recently, quantum computations are gaining widespread popularity. If in a classical computer the smallest unit of information is represented by a bit, which can take the value of either 0 or 1 at one time, then in quan- tum this role is played by qubits . Their peculiarity is that the qubit can be both in state 0 and state 1 at the same time . This gives quantum computers their superior processing power. For example, if we consider four bits of information, then from all 16 possible states we can choose only one at a time. 4 qubits can be in 16 states at the same time, that is, in superposition , and this relationship grows exponentially with each new qubit.

If in a classical computer logical elements receive information bits as input, and the output produces a uniquely defined result, then in a quantum computer, a so-called quantum gate (quantim gate) is taken as a logical element, which manipulates the value of the whole superposition.

An important phenomenon inherent in cubits is confusion . For example, we have two entangled qubits. Measuring the state of one of them will help to find out information about the state of his pair without the need for any verification.

It should be noted that a quantum computer is not a replacement for the classic we are used to, since they are faster only in performing computational operations, where it is necessary to use all sorts of superpositions. So, it is completely inexpedient to use such a machine for watching videos with cats.

On the one hand, the emergence of a quantum computer is awesome. Seriously. In many areas of science, such a machine will bring many benefits (for example, in modeling), but for cryptography such a significant breakthrough will be critical. And all because in 1994 Peter Shore proposed a quantum algorithm that allows decomposing a number, not for hundreds of years, but for a quite observable time.

About Shor's algorithm

Modification of this algorithm allows solving the discrete logarithm problem. Generally, Shor's method consists in reducing a task that is difficult to calculate on a classical computer to the calculation of the order of a certain function. If we consider the factorization of a number, or the factorization problem, then the function itself is taken as $$$f (x) = a ^ x (mod \, N)$ where $$$N -$ the number that unfolds, and $$$a -$ specially selected value, mutually simple with $$$N$ . Further in the course of the algorithm is the period of the function. $$$w$ which satisfies the relation: $$$f (x + w) = f (x)$ and, as a result, executed $$$a ^ w = 1 (mod \, N)$ . For the period found, calculate your own divisor of the number $$$N$ possible using the Euclidean algorithm : $$$gcd (a ^ \ frac {w} {2}, N)$ .

In order to solve the problem of discrete logarithmization, that is, to find such $$$k$ according to $$$y = g ^ k$ It is necessary to calculate the order of another function, namely: $$$f (x_1, x_2) = g ^ {x_1} y ^ {x_2}$ where $$$g -$ the generator of the group with the number of elements equal to $$$q$ . The period of the function is represented by a pair of numbers. $$$(w_1, w_2)$ : $$$f (w_1 + x_1, w_2 + x_2) = f (x_1, x_2)$ . Then the solution of the discrete logarithm problem will be: $$$k = - \ frac {w_1} {w_2} (mod \, q)$ .

Thus, in the Shor method, the quantum and classical parts can be distinguished, and the task of the quantum part of the algorithm is to find the period of the function using the superposition method.

Not surprisingly, the existence of such algorithms and the trend towards the development of quantum computers have pushed specific organizations to think. The US National Security Agency, for example, in 2015, announced a plan for the transition to algorithms that are resistant to an attack on a quantum computer. And in 2016, NIST USA officially announced the launch of a tender for the development of post-quantum cryptography algorithms.

Post-quantum cryptography is not limited to one primitive, in fact, at the moment there are several candidates under consideration. These may include, for example, fast cryptographic protocols on lattices , schemes on hash functions (for example, the Merkle signature ) and cryptosystems based on non-commutative algebra (for example, on the braid group). We stopped our choice on an alternative closely related to elliptic curves (after all, we love them so much!), Namely, with isogeny .

4. Isogeny will save us!

Let's start with the concept: isogeny is a rational mapping that takes the points of one elliptic curve to the points of an isogenic curve, keeping the point at infinity that is fixed. Suppose we have two isogenic elliptic curves. $$$E_1$ and $$$E_2$ . They are called isogenic if they are set over one field and have the same number of points.


So, isogeny is, in fact, a small pinch that takes a curve point $$$E_1$ at the input, and at the output gives a point curve $$$E_2$ . The core of isogeny is the set of points on a curve. $$$E_1$ that go to an infinitely distant point of a curve $$$E_2$ .

For each isogeny, there is a single dual isogeny that performs the inverse transform. That is, if isogeny has the following form: $$$\ phi: E_1 \ rightarrow E_2$ , then dual to it: $$$\ hat {\ phi}: E_2 \ rightarrow E_1$ .

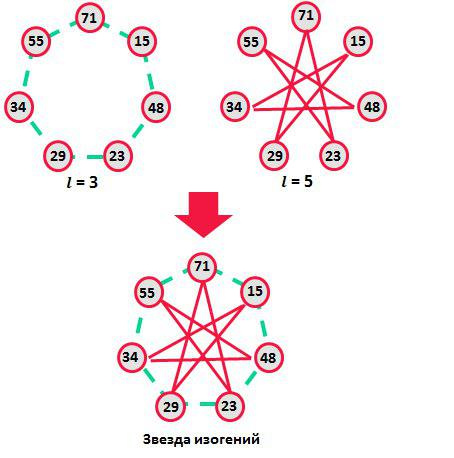
If we multiply the isogeny and its dual, we get the point of the curve $$$E_2$ multiplied by an integer $$$l$ which is called the degree of isogeny . Isogeny simple degrees can specify permutations on the set $$$j-$ invariants of isogenic curves. And the sequential imposition of graphs of isogenic elliptic curves makes it possible to obtain just a cosmically beautiful star of isogenic curves , as in the figure below.

The possibility of using isogeny to build cryptosystems was proposed relatively recently. In 2003, the author E. Teske published a work where isogeny was used in a scheme with the ability to deposit keys. In 2006, A. G. Rostovtsev and A. Stolbunov, the El-Gamal encryption scheme was adapted to the isogeny of elliptic curves. In the same 2006, it was proposed to use graphs of isogenic super-singular curves for constructing hash functions. An important and, one can say, a turning point in the study of isogeny is the paper published in 2010, where a quantum algorithm is proposed that solves the problem of finding the isogeny of non-supersingular curves in subexponential time. From this point on, studies have become more focused on supersingular curves. Thus, the network can already find encryption schemes with a public key, evidence with zero disclosure , a scheme of indisputable signature and signature blindly .

5. Microsoft SIDH: what a pokemon?

Microsoft also did not stand aside and in 2016 released the open source library SIDH (Supersingular Isogeny Key Exchange). One of the advantages of this library is the possibility of using elliptic curves in the form of Montgomery, which protect against time attacks.

SIDH is implemented in C and supports the use of Microsoft Visual Studio on Windows OC and LNU GCC and clang on Linux OC. The library presents the implementation of basic arithmetic functions with the ability to support various platforms, including x64, x86 and ARM. A big plus to performance is an optimized implementation of operations on elliptic curves.
In the library, the Diffie-Hellman key separation protocol is implemented on the isogeny of super-singular curves.

This scheme was proposed by the authors Jao and DeFeo. Simplified it can be described as follows. The well-known super-singular curve is used as the cryptosystem parameters. $$$E_0$ and points fixed on it $$$P_A, Q_A, P_B, Q_B$ . For convenience, the progress of the protocol can be seen in the figure below.

Let Alice want to share with Bob not a life, but a private key. For this, it generates random numbers. $$$m_A, n_A$ and builds isogeny $$$\ phi_A: E_0 \ rightarrow E_A$ where the kernel is given as $$$<m_A P_A + n_AQ_A>$ .
Bob performs the same actions, but only builds isogeny. $$$<m_B P_B + n_BQ_B>$ where as the core is selected $$$<m_B P_B + n_BQ_B>$ .

Isogeny $$$\ phi_A$ and $$$\ phi_B$ are secret and are not transmitted to anyone. However, both Bob and Alice can divide the points on their isogenic curves without any consequences; moreover, the curves themselves can be transmitted. This is actually happening. This stage is indicated in the figure by a dotted line. Alice passes points to Bob $$$\ phi_A (P_B)$ and $$$\ phi_A (Q_B)$ and the curve itself $$$E_A$ . Bob does the same thing: passes Alice points $$$\ phi_B (P_A)$ and $$$\ phi_B (Q_A$ and curve $$$E_B$ .

Is it even legal ?! You can be calm, % username% , knowing both isogenic curves, the attacker will not be able to calculate the isogeny itself.

So, Alice and Bob exchanged data, now we come to the final and incredibly beautiful stage, namely, to obtain a common key. Knowing the images of points $$$P_A$ and $$$Q_A$ on the curve $$$E_B$ and random numbers $$$m_B$ and $$$n_B$ , Bob can easily build isogeny $$$\ phi'_A$ , and Alice, having the same amount of information, can build isogeny $$$\ phi'_B$ . The elegant solution is that isogeny $$$\ phi'_A$ and $$$\ phi'_B$ will lead our interlocutors to the curve $$$E_ {AB}$ and as a key it can be taken $$$j-$ invariant.

Microsoft has significantly simplified life by implementing basic functions that exempt the above steps of the algorithm from coding. Before you implement a key sharing scheme, you need to initialize the structure, which contains the cryptosystem parameters:

CurveIsogeny = SIDH_curve_allocate(CurveIsogenyData); if (CurveIsogeny == NULL) { Status = CRYPTO_ERROR_NO_MEMORY; goto cleanup; } Status = SIDH_curve_initialize(CurveIsogeny, &random_bytes_test, CurveIsogenyData); if (Status != CRYPTO_SUCCESS) { goto cleanup; } 

The structure itself:

 typedef struct { CurveIsogeny_ID CurveIsogeny; unsigned int pwordbits; unsigned int owordbits; unsigned int pbits; uint64_t prime[MAXWORDS_FIELD]; uint64_t A[MAXWORDS_FIELD]; uint64_t C[MAXWORDS_FIELD]; unsigned int oAbits; uint64_t Aorder[MAXWORDS_ORDER]; unsigned int oBbits; unsigned int eB; uint64_t Border[MAXWORDS_ORDER]; uint64_t PA[2*MAXWORDS_FIELD]; uint64_t PB[2*MAXWORDS_FIELD]; unsigned int BigMont_A24; uint64_t BigMont_order[BIGMONT_MAXWORDS_ORDER]; uint64_t Montgomery_R2[MAXWORDS_FIELD]; uint64_t Montgomery_pp[MAXWORDS_FIELD]; uint64_t Montgomery_one[MAXWORDS_FIELD]; } CurveIsogenyStaticData; 

In order for Alice and Bob to exchange keys, it is enough to call a couple of functions that do not oblige to know what is happening “under the hood”. Key generation takes place using functions:

 Status = KeyGeneration_A(PrivateKeyA,PublicKeyA, CurveIsogeny); 

and

 Status = KeyGeneration_B(PrivateKeyB,PublicKeyAB CurveIsogeny); 

Alice and Bob exchange the calculated public keys and find the common key:

 Status = SecretAgreement_A(PrivateKeyA, PublicKeyB, SharedSecretA, false, CurveIsogeny); 

and

 Status = SecretAgreement_B(PrivateKeyB, PublicKeyA, SharedSecretB, false, CurveIsogeny); 

Among the functions in the library can be distinguished and basic arithmetic, which will help in the implementation of their protocols. These are, for example, j_inv, which calculates the j-invariant of an elliptic curve, inv_3_way, which finds the multiplicative value of the inverse, doubling a point and adding points - xDBLADD, tripling a point - xTPL, etc. A full description can be found in the publication .

6. It's coding time!

In order not to be unfounded and to touch a bright future in the face of post-quantum cryptography, we decided to test the applicability of this library using the example of a device with relatively limited power — a mobile phone. As a result, a voting application was implemented on Android OC. Its chip is the implementation of post-quantum cryptography to encrypt the sent voice on the device and its decryption on the server.

Encryption itself, as is clear from the library’s name, is not implemented there, therefore, having armed ourselves with a publication , we implemented an encryption scheme. The final protocol is not much different from the original.

So, we have the well-known curve $$$E_0$ , the same four points on it $$$P_A, Q_A, P_B, Q_B$ , two quantum paranoids and a strong desire to communicate. Initialize the structure with the cryptosystem parameters:

 CurveIsogeny = SIDH_curve_allocate(CurveIsogenyData); Status = SIDH_curve_initialize(CurveIsogeny, &random_bytes_test, CurveIsogenyData); 

The public key here is presented as a tuple of values: $$$E_A, \ phi_A (P_B), \ phi_A (Q_B)$ and random number $$$k$ . The private key is represented by numbers. $$$m_A$ and $$$n_A$ by which isogeny is built $$$\ phi_A: E_0 \ rightarrow E_A$ .

 Keys.PrivateKey = (unsigned char*)calloc(1, obytes); Keys.PublicKey = (unsigned char*)calloc(1, 4 * 2 * pbytes); random_bytes_test(10, Keys.k); Status = KeyGeneration_A(Keys.PrivateKey, Keys.PublicKey, CurveIsogeny); 

During the encryption step, Bob generates random values. $$$m_B$ , $$$n_B$ and builds isogeny $$$\ phi_B: E_0 \ rightarrow E_B$ . Using public key values ​​passed to him $$$E_A, \ phi_A (P_B), \ phi_A (Q_B)$ , Bob, building isogeny $$$\ phi'_B: E_A \ rightarrow E_ {AB}$ , goes into a general curve.

 Status = KeyGeneration_B(IsogenyB, imagesB, CurveIsogeny); Status = SecretAgreement_B(IsogenyB, PublicKey, j, false, CurveIsogeny); 

Then you can exhale. $$$j-$ common curve invariant $$$E_ {AB}$ concatenated with a number $$$k$ , and this hash is taken from this hash. The resulting value is broken with secret data. In the case of an application, this is a hash from the title of the report.

 strncat(j, k, 10); shaCompute(j, hash); for (i = 0; i < strlen(message); i++) message[i] ^= hash[i]; 

Alice takes a tuple of values $$$E_B, \ phi_B (P_A), \ phi_B (Q_A)$ and the meaning of the ciphertext. According to the data she builds isogeny $$$\ phi'_A$ , goes into a general curve $$$E_ {AB}$ and using her $$$j-$ invariant, decrypts the message.

 Status = SecretAgreement_A(PrivateKey, imagesB, j, false, CurveIsogeny); strncat(j, k, 10); shaCompute(j, hash); for (i = 0; i < strlen(cipher); i++) cipher[i] ^= hash[i]; 

When the application is launched, a request is sent to the server, in response to which a list of reports comes. If the user wishes to vote (well, when the corresponding button is clicked), the server sends the open parameters necessary for voice encryption. The client, without being lost, uses these parameters, thinks about 5-8 seconds, and sends the necessary parameters for decryption and the cipher text. The server decrypts this business in some 0.11 seconds and gives the client the results of the vote.

In order to "make friends" Java and C, JNI technology was used. SIDH is compiled into the library and connected in java code:

 static { System.loadLibrary("native-lib"); } 

The developed application could be downloaded on the NeoQUEST " confrontation " on June 29, 2017! Many listeners took the opportunity to touch, probably, the future direction in the field of cryptography and voted for the report they liked. And every voice was protected from attacks on a quantum computer! Well, and still - the app is beautiful!

In conclusion...

Of course, while it is difficult to judge the need for post-quantum cryptography, when a powerful quantum computer, in fact, and no ... However, the fuss in the NSA and NIST can not lead to suspicion. We can only guess about the real motives of such haste. In any case, it never hurts to play it safe and start exploring a new and interesting direction in cryptography, especially if it is quite feasible in practice.

If you are interested in the implementation of the application, and if you want to write something new, you are welcome to the source !

Very soon we will post on our youtube-channel video reports from the “confrontation” NeoQUEST-2017, where there will be, among other things, a recording of a report about elliptic curves and post-quantum cryptography!

Well, we have already posted photos from NeoQUEST-2017 in the NeoQUEST group on VKontakte . In the near future, wait for new articles, including hackquest job descriptions (hidden from the “Head-to-Head" guest)!