Postquantum reincarnation of the Diffie-Hellman algorithm: probable future (isogeny)

Today we will again talk about the Diffie-Hellman protocol, but already built on more unusual constructions - isogeny, which are considered resistant to attacks on the future quantum computer. A quantum computer that can keep in the bound state of the order of several thousand qubits, will allow you to find the private keys of the public keys of all asymmetric cryptosystems currently used. The number of qubits for breaking RSA is equal to twice the number of bits in the module (i.e., the factoring of the RSA module with a length of 2048 bits will require 4096 qubit). For breaking elliptic curves, more modest “quantum iron” powers are needed: to solve the ECDLP problem for curves over a simple field (there are such curves in the national standard GOST R 34.10-2012 and in American ECDSS) with a n-bit curve modulus (i.e., for a 256-bit module, you need ~ 1536 qubit, and for 512 bits ~ 3072 qubit). The other day a Russian-American group of scientists set a world record, keeping 51 quits in a bound state. So we have a little more time to study isogeny (as well as grids, codes, multivariate, and hash-based signatures).
By the way, isogeny is considered one of the most likely candidates for winning a postquantum algorithm in the NIST competition to replace RSA and elliptic curves in the next few years. The previous article about the past and present Diffie-Hellman can be read here .

What is isogeny?

A mapping that takes points of one curve E1 to points of another curve E2 (or to itself (then we assume E2 = E1)) as follows: if on the curve E1 we choose any two points A1 and B1 and map them to points A2 and B2 on curve E2, then the same mapping will necessarily transfer their sum — the point C1 = A1 + B1 precisely to the point C2 = A2 + B2 — the sum of their maps. This remarkable property is called operation preservation, and this mapping is a homomorphism. Isogeny can be expressed using a rational function: the point (x, y) is mapped to a point with coordinates $$$(\ frac {f1 (x, y)} {f2 (x, y)}, \ frac {g1 (x, y)} {g2 (x, y)})$ (Where $$${f1, f2, g1, g2}$ - polynomials).
If there is such a mapping between two curves, then they are called isogenic. A particular case of isogeny is the isogeny of a curve on itself (endomorphism).
')
What property should have two curves to be isogenic?

Tate theorem:
Two curves over a single finite field are isogenous if and only if the orders of their groups are equal.

Example 1 (isogeny of a curve on itself):

Endomorphism: scalar multiplication of a point by a number: $$$n * P$ on the curve $$$y ^ 2 = x ^ 3 + Ax + B$
for example, for n = 2 and $$$P = (x, y)$ :

$$$2 * P = (\ frac {x ^ 4 - 2Ax ^ 2 - 8Bx - A ^ 2} {4 (x ^ 3 + Ax + B)}, \ frac {(x ^ 6 + 5Ax ^ 4 + 20Bx ^ 3 -5A ^ 2x ^ 2-4ABx - 8B - A) y} {8 (x ^ 3 + Ax + B) ^ 2})$

For an arbitrary n, a similar (but longer) formula can be obtained recursively using so-called division polynomials.

Example 2 (isogeny between different curves):

Let there be a curve $$$E1: y ^ 2 = x ^ 3 + x + 1$ over the field $$$GF (19)$
and curve $$$E2: y ^ 2 = x ^ 3 + 4x + 13$ over the same field.

The group orders (i.e., the number of points on the curve) for E1 and E2 are: # E1 = # E1 = 21

By the Tate theorem, the equality # E1 = # E1 means that there is isogeny between E1 and E2.
j – the invariant E1 = 6, and j – the invariant E2 = 4. That is, the groups of points of the curves are not isomorphic.
(an isomorphism is a special case of a homomorphism, when only one element of the image corresponds to each element in the map (that is, several elements do not become one: the map is “one to one”))

The isogeny, which maps points from E1 to E2 (from where it came from, we will show in Example 3) can be represented using the following rational mapping:

Display $$$φ: (x, y)$ → $$$(\ frac {x ^ 3-4x ^ 2-8x-8} {x ^ 2-4x + 4}, \ frac {x ^ 3y-6x ^ 2y + 5xy-6y} {x ^ 3-6x ^ 2 -7x-8})$

Consider, for example, points A1 (9, 6) and B1 (14, 2) of the curve E1. Their sum is the point C1 with coordinates (5, 6). If we substitute them in the formula above, we get their mapping onto the curve E2, the corresponding points on E2 - A2, B2, C2:

A1 (9, 6) → A2 (14, 1)
B1 (14, 2) → B2 (17, 4)
C1 (5, 6) → C2 (8, 5)

It is easy to verify that C2 = A2 + B2. Those. point C1 = A1 + B1 goes to point C2 = A2 + B2. If not laziness, then you can iterate through all combinations of any two points E1 A and B and their mappings φ (A) and φ (B) and make sure that they behave similarly:

$$$φ (A + B) = φ (A) + φ (B)$

And what will happen if we substitute points (2, 12) or (2, 7)? The denominator of the right fraction will be zero! It just means that these points go to a point at infinity for E2.
It remains to consider a point at infinity on E1. It “defaults” to the point at infinity at E2. This is a fundamental property of a homomorphism: the neutral element (in the case of elliptic curves it is a point at infinity) is mapped into a neutral element. Otherwise, the operation will “break” for the case when one of the two elements is neutral.
The degree of isogeny is the degree of a polynomial. $$$f1$ in the display formula $$$(\ frac {f1 (x, y)} {f2 (x, y)}, \ frac {g1 (x, y)} {g2 (x, y)})$
In Example 2 $$$f1 = x ^ 3 - 4x ^ 2 - 8x - 8$ Those. the degree of isogeny is equal to 3. The degree means that how many times the display “shrinks” the image. Those. 3 different points of E1 are displayed with this isogeny in one point on E2. The set of points that map to a point at infinity is called the core of isogeny.

Isogeny Calculation

How to find such a display? It turns out that the number of possible isogenies for a particular curve is equal to the number of subgroups in the group of its points. There is a deterministic algorithm that was invented by the mathematician Velu 'in 1971. It uses many formulas, so we first show its general scheme:

Entrance:
curve $$$E1: y ^ 2 = x ^ 3 + Ax + B$ and one of its subgroups $$$C$ (isogeny kernel)

Output:
curve $$$E2: y ^ 2 = x ^ 3 + A'x + B '$ isogenic $$$E1$ and rational mapping $$$(\ frac {f1 (x, y)} {f2 (x, y)}, \ frac {g1 (x, y)} {g2 (x, y)})$

Algorithm complexity: $$$O$ (# $$$C$ ) steps where # $$$C$ - order $$$C$

Designation: $$$E → E / C$ where $$$E / C$ isogenic curve
$$$E$ obtained using subgroups $$$C$

At the output we get the coefficients $$$A '$ and $$$B '$ for the isogenic curve and the formula with fractions. Subgroup C - any of the subgroups of the curve. C is the core of isogeny: all its elements go to a point at infinity. If the E1 curve is isogenic to the E2 curve, then the opposite is also true: E2 is isogenic to E1: there is a homomorphic mapping in the opposite direction.

And now we will explain why we have all this piled up (and we will continue to do this):
as well as for multiplicative groups of a finite field and elliptic curves, for isogeny, there is a complex task that can (and should) be used to create digital signature and Diffie-Hellman analogs.

Challenge for isogeny:
Two isogenic curves are given. $$$E1$ and $$$E2$ with different j-invariants. It is required to find the isogeny between them.

If we have two curves, about which we know that they are isogenic (and this is so, if the orders of their groups are equal), but we do not know with the help of which subgroup this isogeny can be obtained. Obviously, the number of subgroups must be large enough so that it is computationally difficult to find isogeny by simple enumeration, substituting subgroups into the Velu 'algorithm.

Velu 'algorithm:

Entrance:
curve $$$E1: x ^ 3 + Ax + B$ and one of its subgroups $$$C$ (core isogeny)

1. Drop the point at infinity
2. Find $$$C_2$ - a set of points of even order from $$$C$ .
$$$R$ - other
3. We break $$$R$ in two parts - $$$R _ {+}$ and $$$R _ {-}$ : if point P is in $$$R _ {+}$ , then the opposite to her - in $$$R _ {-}$
4. The set $$$S = C_2 ∪ R _ {+}$

For each point $$$Q = (x_Q, y_Q)$ of $$$S$

$$$g_ {Q} ^ x = 3x_ {Q} ^ 2 + A$
$$$g_ {Q} ^ y = -2y_ {Q}$

$$$if (Q = -Q)$
$$$v_ {Q} = g_ {Q} ^ x$
$$$else$
$$$v_ {Q} = 2g_ {Q} ^ x$

$$$u_ {Q} = (g_ {Q} ^ y) ^ 2$

$$$v = \ sum_ {Q ∈ S} (v_ {Q})$
$$$w = \ sum_ {Q ∈ S} (u_ {Q} + x_ {Q} v_ {Q})$

Coefficients $$$A '$ and $$$B '$ for the isogenic curve equation $$$E '$ :
$$$A '= A - 5v$
$$$B '= B - 7w$

So, we know the isogenic curve. How to calculate mapping $$$(x, y)$ → $$$(α, β)$ :

$$$α = x + \ sum_ {Q ∈ S} (\ frac {v_Q} {(x-x_Q)} + \ frac {u_Q} {(x-x_Q) ^ 2})$
$$$β = y - \ sum_ {Q ∈ S} (u_Q \ frac {2y} {(x-x_Q) ^ 3} + v_Q \ frac {y - y_Q} {(x-x_Q) ^ 2} - \ frac { g_Q ^ xg_Q ^ y} {(x-x_Q) ^ 2})$

Velu 'algorithm output:
Coefficients $$$A '$ , $$$B '$ isogenic curve and the formula for displaying points $$$(x, y)$ → $$$(α, β)$

Example 3 (Velu 'Algorithm. How the isogeny was obtained in Example 2):

Entrance :
$$$y ^ 2 = x ^ 3 + x + 1$ over the field $$$GF (19)$ and subgroup $$$C$ : { $$$O$ , $$$(2, 7)$ , $$$(2, 12)$ }

1. Drop the point at infinity
2. There are no even order points $$$C$ not
3. Choose for $$$R _ {+}$ the point $$$(2, 7)$ . Point $$$(2, 12)$ - it is inverse (since 7 = -12 mod 19)
4. The set $$$S$ = { $$$(2, 7)$ }

One step cycle: (because $$$S$ only one element: point $$$Q = (2, 7)$ ):

$$$Q = (2, 7)$ its coordinates $$$x_Q = 2, y_Q = 7$
$$$g_Q ^ x = 3 * 2 ^ 2 + 1 = 13$
$$$g_Q ^ y = -2 * 7 = -14 = 5$$$$mod$$$$19$
$$$v_Q = 2 * 13 = 26$$$$mod$$$$19 = $$
$$$u_Q = 5 ^ 2$$$$mod$$$$19 = 6$
$$$v = 7$
$$$w = 6 + 2 * 7 = 20 = 1$$$$mod$$$$19$
$$$A '= A - 5v = 1 - 5 * 7 = - $ 3$$$$mod$$$$19$ = $$$4$
$$$B '= B - 7w = $ 1$

It remains only to calculate the rational mapping: $$$(x, y) → (α, β)$ :
$$$α = x + \ frac {7} {x-2} + \ frac {6} {(x-2) ^ 2} = \ frac {x ^ 3-4x ^ 2-8x-8} {x ^ 2 -4x + 4}$

Similarly, we bring the formula for β to a common denominator:
$$$β = \ frac {x ^ 3y-6x ^ 2y + 5xy-6y} {x ^ 3-6x ^ 2-7x-8}$

Output:
The coefficients of the isogenic curve: $$$A '= 4, B' = $ 1$
Display $$$(x, y) → (α, β)$ (see above).

Large degree isogeny computation

It is easy to see that in the Velu algorithm there are pitfalls: it works in a cycle until it passes through all points from the set $$$S$ . This means that the number of steps will be more than half the order of the core of isogeny (subgroups $$$C$ which is fed to the input) and less than the order $$$C$ . Velu can only use relatively small subgroups so that it is possible to go through all the steps of the algorithm at an acceptable time, which complicates the cryptographic application of isogeny. Fortunately, there is a method that allows you to quickly calculate isogeny, even if the group $$$C$ has a big order $$$C$ but has a certain structure: if # $$$C$ - the degree of a small number $$$l$ i.e. $$$l ^ e$ . In this case, the algorithm consists of e steps, each of which considers the isogeny degree $$$l$ over Velu 'and one scalar multiplication of a point by a number. As $$$l$ usually choose 2 or 3.

Designation: Curve $$$E '$ isogenic $$$E$ obtained using subgroups $$$C$ instead of $$$E$ / $$$C$ It is sometimes much more convenient to mark with a dot. $$$G$ - generator $$$C$ : $$$E / <$$$$G$$$$>$ .

Let be $$$G$ - point of order $$$l ^ e$ . It is necessary to calculate the isogeny $$$φ: E → E / <$$$$G$$$$>$ .
Decompose isogeny $$$φ$ on a sequence of isogeny, where each has a degree $$$l$$$$φ_ {e-1} * φ_ {e-2} * ... * φ_ {0}$ :
$$$φ_0: E, G_0 = G$
$$$φ_i: E_ {i + 1} = E_i / <$$$$l ^ {e-1-i} G_i$$$$>$ , $$$G_ {i + 1} = φ_i (G_i)$

Example 4
We want to calculate the isogeny for the cyclic order group $$$l ^ 4$
Instead of once applying the Velu 'algorithm for a group, we apply it 4 times, each time counting the isogeny of the degree $$$l$ and 3 times multiply the point by the number. Let be $$$G_0$ - generator of this group, point of order $$$l ^ 4$ .

$$$φ_ {3}$ * $$$φ_ {2}$ * $$$φ_ {1}$ * $$$φ_ {0}$ :

$$$φ_0: E_1 = E_0 / <$$$$l ^ {3} * G_0$$$$>$ , $$$G_1 = φ_0 (G_0)$

$$$φ_1: E_2 = E_1 / <$$$$l ^ {2} * G_1$$$$>$ , $$$G_2 = φ_1 (G_1)$

$$$φ_2: E_3 = E_2 / <$$$$l ^ {1} * G_2$$$$>$ , $$$G_3 = φ_2 (G_2)$

$$$φ_3: E_4 = E_3 / <$$$$G_3$$$$>$

So, now we are able to calculate isogeny for cyclic groups of very large order. For example, if there is a group of order $$$2 ^ {256}$ and we know its generator, then we will go through the algorithm in 256 steps.

Practice: isogeny between supersingular curves

Recall that the two isomorphic curves have the same j-invariant and for the curve $$$y ^ 2 = x ^ 3 + Ax + B$ he is equal $$$1728 \ frac {4A ^ 3} {4A ^ 3 + 27B ^ 2}$
Due to the fact that it is not particularly difficult to find a transformation between isomorphic curves, the isogeny problem is essentially a problem of finding isogenies between different classes of isomorphic curves (and each of these classes can be represented as a corresponding j-invariant).
What curves are of interest for isogeny? After all, we know that there are forbidden families of curves for elliptic Diffie-Hellman and EDS: supersingular, anomalous, and smooth order, etc. - for all, the problem of ECDLP is relatively easy to solve. Such unpleasant classes must exist for isogeny. Only here the situation is completely different, because the difficult task is not ECDLP. Obviously, it is necessary to use curves of smooth order in order to have more subgroups. In addition, in 2010, researchers from the University of Waterloo found out that using ordinary curves is unsafe from a “quantum” point of view: a result was obtained that stated that it is safe to use only super-singular curves for cryptosystems using isogeny. Recall that these are curves in which the Frobenius trace t is such that t mod p = 0, where p is a characteristic of the curve field (the Frobenius trace itself is related to the order of the curve group # $$$E (GF (p ^ n))$ and field ratio # $$$E (GF (p ^ n)) = p ^ n + 1 - t)$ . Further we will consider only them.

What field for a curve would be more optimal to use? The answer immediately suggests itself: the good old simple field. $$$GF (p)$ . But unfortunately, the supersingular curves over $$$GF (p)$ There are too few different j-invariants: ~ $$$\ sqrt {p}$ . Whereas for the field $$$GF (p ^ 2)$ , number of j-invariants # $$$S_ {p ^ 2} = \ lfloor p / 12 \ rfloor + a$ where $$$a ∈$ { $$$1, 2, 3$ }

Such curves have interesting properties:
The isogeny graph of a fixed degree is correct. (i.e. each vertex has the same number of edges)
For any prime number $$$l$ which divides the order of a group of points of a curve exists $$$l + 1$ core isogeny with order $$$l$ . (i.e. there is $$$l + 1$ order subgroup $$$l$ , with which you can get isogeny)

Example 5 (example and graph images - Dr. Fre Vercauteren)
Consider the field $$$GF ({241 ^ 2})$
Choose an irreducible polynomial: $$$x ^ 2 - 3x + 7$
The set of j-invariants will be:
$$$S_ {241 ^ 2}$ = {93, 51w + 30, 190w + 183, 240, 216, 45w + 211, 196w +
105, 64, 155w + 3, 74w + 50, 86w + 227, 167w + 31, 175w + 237, 66w + 39, 8, 23w + 193, 218w + 21, 28, 49w + 112, 192w + 18}
Their number $$$S_ {241 ^ 2}$ = 20

For order curves $$$E$ = 57600 = $$$2 ^ 8 * 3 ^ 2 * 5 ^ 2$ :

For isogeny degree $$$l = 2$ :
Each curve has 3 isogeny degrees 2


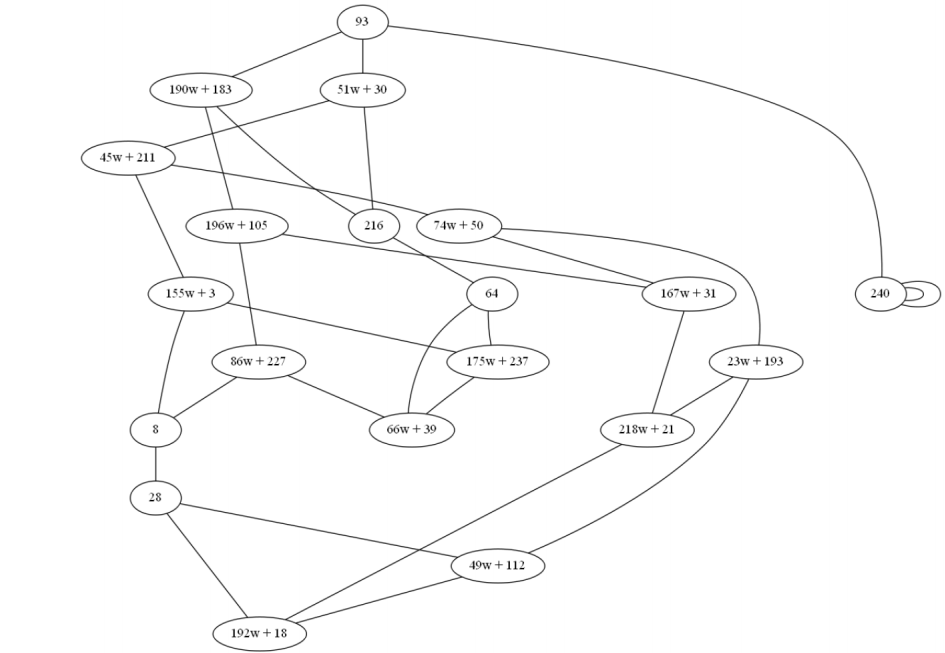
For isogeny degree $$$l = 3$ :
Each curve has 4 isogeny degrees 3


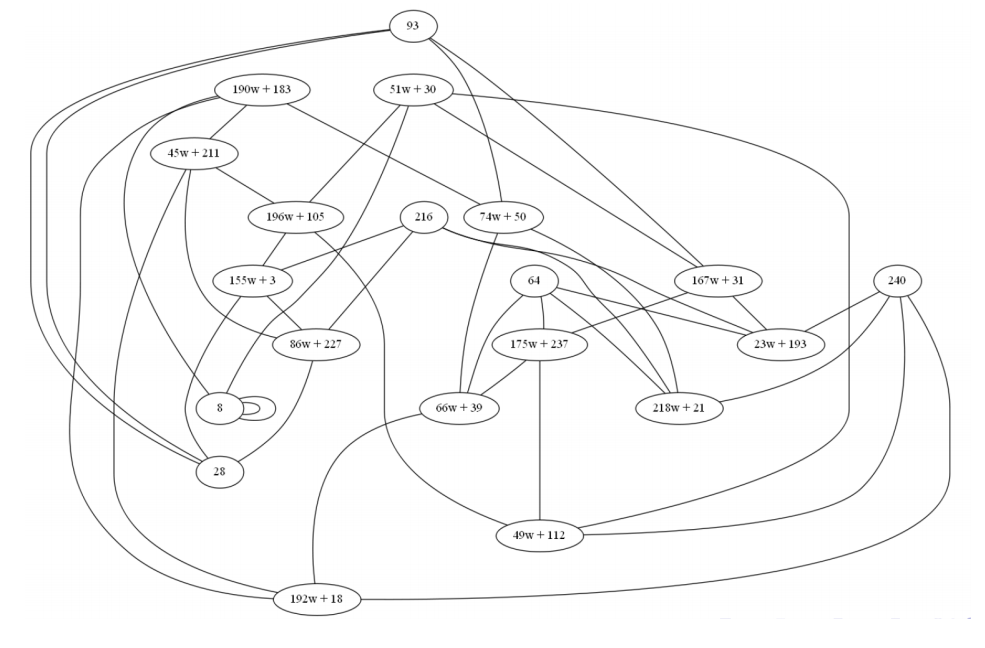
Similarly for $$$l = 11$ .
Each curve has 12 isogeny degrees of 11.

The difficult task that the attacker will have to solve now can be formulated as follows: knowing two curves $$$E1$ and $$$E2$ (i.e. knowing two $$$j$ -invariant $$$j1$ and $$$j2$ ), find the path in the isogeny graph between them. Essentially - find a method for obtaining isogeny between curve c $$$j1$ and curve c $$$j2$

Supersingular Isogeny Diffie-Hellman (SIDH)

Definition:
If when multiplying a point $$$P$ crooked $$$E (GF (p ^ m))$ multiplying by n, we get a point at infinity, then this point is called an n-torsion point (n-torsion point)
N-torsion subgroup (n-torsion subgroup) $$$E [n]$ :
$$$E [n] =$ { $$$P ∈ E (GF (p ^ m)): n * P = O$ }
This subgroup consists of a point at infinity and all n-torsion points.
Obviously, an n-torsion point is a point if its order divides n without a remainder.

$$$E [n]$ isomorphic to direct product $$$(Z / nZ) × (Z / nZ)$ when n is coprime with p. (i.e. order $$$E [n]$ equals $$$n ^ 2$ )

Field selection $$$GF (p ^ 2)$ for curves for SIDH:
Let be $$$f$ - a small number, and $$$l_a, l_b$ - small prime numbers.
When characterizing the field $$$p = l_a ^ {e_a} * l_b ^ {e_b} * f ± 1$ curve order $$$E$ : # $$$E = (l ^ {e_a} * l ^ {e_b} * f) ^ 2$
$$$E [l ^ {e_a}]$ contains $$$l_a ^ {e_a - 1} (l_a + 1)$ cyclic order subgroups $$$l_a ^ {e_a}$

So let $$$l_a = 2, l_b = 3$
field characteristic $$$p = 2 ^ {m} * 3 ^ {n} * f ± 1$ , and n and m will be chosen so that $$$2 ^ {m}$ was approximately equal $$$3 ^ {n}$
Torsion subgroups $$$E [2 ^ m]$ and $$$E [3 ^ n]$ ⊆ $$$E [p ^ 2]$

$$$E [2 ^ m]$ contains $$$2 ^ {m − 1} * 3$ cyclic order subgroups $$$2 ^ m$
$$$E [3 ^ n]$ contains $$$3 ^ {n − 1} * 4$ cyclic order subgroups $$$3 ^ n$

Pick points $$$P_a, Q_a$ - basis for $$$E [2 ^ m]$ (i.e. using a combination of $$$x * P_a + y * Q_a$ can get any point $$$E [2 ^ m]$ ) and points $$$P_b, q_b$ - basis for $$$E [3 ^ n]$

So the domain parameters for SIDH (analog of domain parameters for ordinary elliptic curves):
curve $$$E$ and two bases { $$$P_a, Q_a$ } and { $$$P_b, q_b$ }. They are known to Alice, Bob and the attacker.


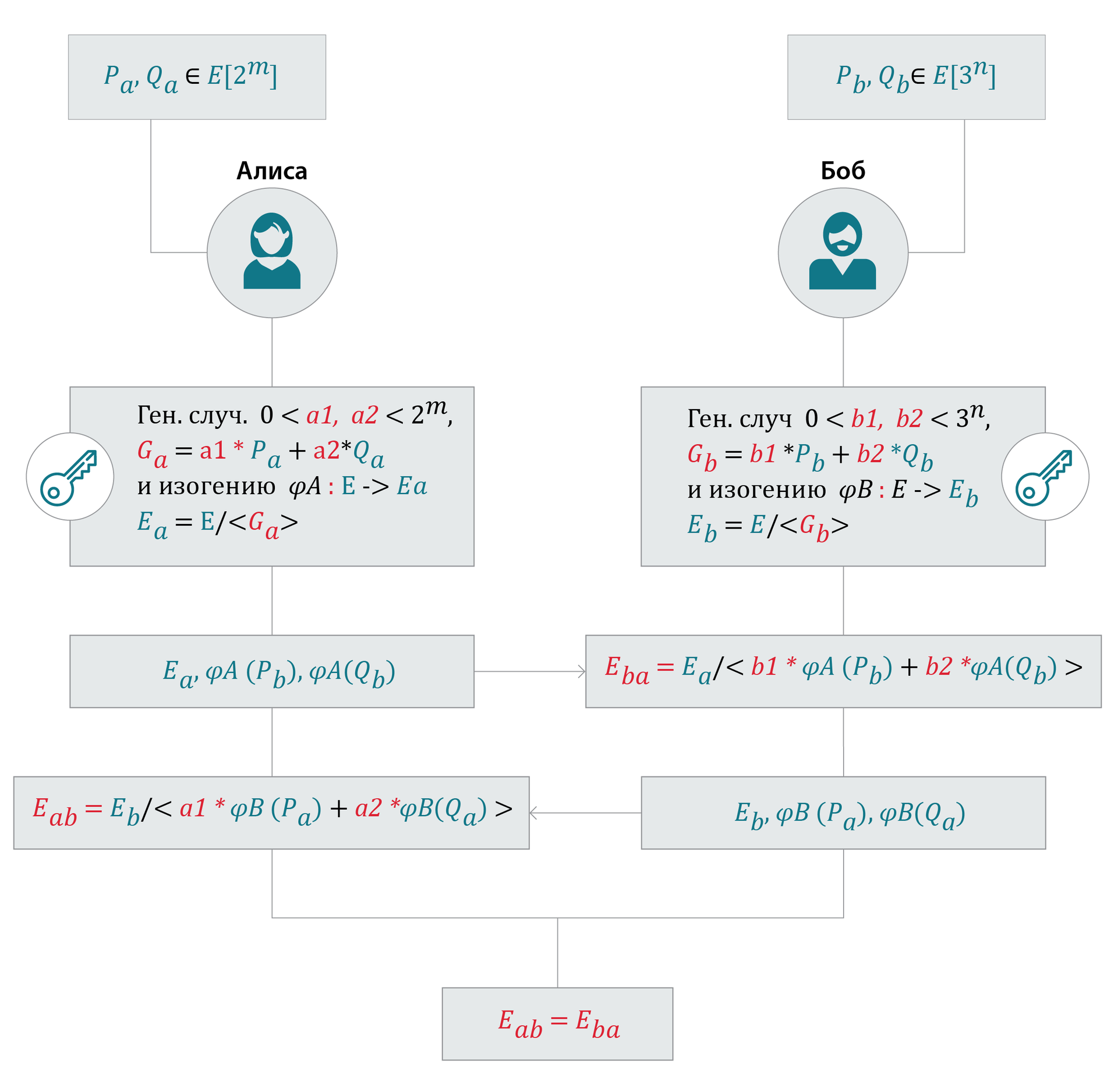
(Note: $$$E_ {ab} = E_ {ba}$ up to isomorphism: the coefficients of the curves may be different, but the j-invariant will be the same)

Whoever starts (Alice) uses a basis for generating a pair $$$P_a, Q_a$ .
Alice generates random $$$a1, a2: 0 <a1, a2 <2 ^ m$ ( $$$a1, a2$ both are not multiples of 2)
$$$a1, a2$ - this is Alice's private key.
It then calculates the calculated point $$$G_a = a1 * P_a + a2 * Q_a$
And it calculates isogeny $$$φA:$$$$E → E_a = E$ / < $$$G_a$ >,
after which it converts using isogeny $$$φA$ Bob's basis on the curve $$$E_a$ : $$$φA ({P_b}), φA ({Q_b})$

Alice's private key: $$$a1, a2$
Alice's public key: the curve $$$E_a$ and points $$$φA ({P_b}), φA ({Q_b})$

Similar steps are taken by Bob (see diagram):
Bob's private key: $$$b1, b2$
Bob's public key: curve $$$E_b$ and points $$$φB ({P_a}), φB ({Q_a})$

Alice sends Bob’s public key
Bob computes a point $$$b1 * φA ({P_b}) + b2 * φA ({Q_b})$ and with its help
isogenic curve $$$E_ {ba} = E_a$ / < $$$b1 * φA ({P_b}) + 2 * φA ({Q_b})$ >

Next, Bob sends Alice the public key and Alice calculates the curve in a similar way. $$$E_ {ab}:$
$$$E_ {ab} = E_b$ / < $$$a1 * φB ({P_a}) + a2 * φB ({Q_a})$ >

To obtain a shared secret, Alice calculates a j-invariant from $$$E_ {ab}$
and Bob from $$$E_ {ba}$ .

Security and key sizes

For a successful attack, you must find a path on at least one of the graphs (Alice or Bob). This task has different degrees of complexity for classical and quantum computers:
Classic difficulty: Alice $$$\ sqrt {2 ^ m}$ , Bob $$$\ sqrt {3 ^ n}$
Quantum complexity: Alice $$$\ sqrt [3] {2 ^ m}$ , Bob $$$\ sqrt [3] {3 ^ n}$
Therefore:
Classic Security = $$$min (\ sqrt {2 ^ m}, \ sqrt {3 ^ n}) ≈ \ sqrt [4] {p}$ operations
Quantum security level = $$$min (\ sqrt [3] {2 ^ m}, \ sqrt [3] {3 ^ n}) ≈ \ sqrt [6] {p}$ operations

Key sizes:

Public key:
P and Q points
coefficients A and B curve

~ 8 * $$$log_2 (p)$ bit
~ 6 * $$$log_2 (p)$ bit (optimization: Costello, Crypto 2016)

Field Characteristic Length = 768 bits:
768/6 = 128-bit quantum security level
768/4 = 192-bit classic security level
Key length 6 $$$log_2 (p)$ bit = 4608 bits = 576 bytes

Field Characteristic Length = 1536 bits:
1536/6 = 256-bit quantum security level
1536/4 = 384-bit classic security level
Key length 6 $$$log_2 (p)$ bit = 9216 bits = 1152 bytes

Performance

Best results for a 128-bit quantum security level (field characteristic $$$p = 2 ^ {372} 3 ^ {239} - 1$ those $$$p$ ~ $$$2 ^ {768}$ ):

For Intel Haswell at a frequency of 3.4 GHz:
calculated for ~ 100 million cycles for one of the parties (Alice or Bob)
(Montgomery curves and projective coordinates are used)

For the ARM7 Beagle Board Black Cortex-A8 chip at 1 GHz:
execution time - 1.5 sec. If you use the NEON SIMD instructions, then 0.2 seconds.

Literature:

1. “Public-Key Cryptosystem Based on Isogenies”, Alexander Rostovtsev, Anton Stolbunov, 2006

2. "Constructing elliptic curve isogenies in quantum subexponential time" Andrew M. Childs, David Jao, Vladimir Soukharev, 2010

3. "Towards Quantum-Resistant Cryptosystems from Supersingular Elliptic Curve Isogenies" David Jao, Luca De Feo, 2011

4. "Efficient algorithms for supersingular isogeny Diffie-Hellman" by Craig Costello and Patrick Longa and Michael Naehrig, 2016

5. “NEON-SIDH: An efficient implementation of supersingular isogeny Diffie-Hellman Exchange protocol on ARM” R. Azarderaksh, D. Jao, 2016

6. “Mathematics of Public Key Cryptography” by Steven D. Galbraith, Cambridge University Press