Systems Management Analysis

Managing something or someone, as a rule, we do not affect the managed system constantly and as a whole. Only from time to time we try to correct it in order to achieve the desired goal. If we quickly determine the moment and place where efforts should be made, the system will slightly deviate from the planned vector of development and will return to the goal we need at the minimum cost.

How to quickly find those elements of the system that need to be corrected? We will try to answer this question today.
')


We will seek a solution not in the area of ​​complex algorithms, which are often difficult to understand and apply. We will talk about simple things that about 70 years ago were the cause of the way out of the crisis for the whole country. Discussed will be the measurement and analysis of mass phenomena. Only such phenomena will be statistically controlled. Why can people consider statistics as evil? Sometimes this is due to the fact that someone with intention or stupidity misleads conclusions based on it. Three examples that many encounter in everyday life.

The mean is only the tip of the iceberg.

We consider the average values ​​of two samples with a volume of 50 from two different general sets. By coincidence, they coincided. And it describes well what the mean value shows us, which is very often used for a brief description of the systems. Instead of listing the incomes of all employees or citizens of the state, they talk about the average value. And as we understand, the average value may be the same for different sets. It may also be the same for the same system at different times. For example, in the example of the income of citizens in a state, there could be an increase in the number of the middle class, and there could be an increase in the wealth of the rich and a greater decline in the income of the poor. Thus, in order to understand the system well, we need to know the law of distribution of quantities in this system.

Need more observations

Secondly, the basis of the statistical study is a set of data on the measurement of one or several signs. The actually observed set of objects, statistically represented by a number of observations of a random variable, is a sample. Hypothetically existing (guessed) - the general population. If the sample size is large enough (n → ∞), the sample is considered large, otherwise it is called a sample of limited size. So, a sample is considered small if, when measuring a one-dimensional random variable, the sample size does not exceed 30 (n <= 30), and when measuring several (k) signs in a multidimensional space simultaneously, the ratio n to k does not exceed 10 (n / k <10 ). Analyzing the statistics for small samples, it is necessary to understand that statistical calculations will have large errors.

"Can not be!"

Thirdly, statistics says nothing about one particular case. Suppose you decide to play a coin toss on the Martingale system. You know that the probability of a tail or a tail is 1/2. You have 15,000 rubles and you decide to bet 1,000 rubles each. You bet 1000 rubles always on the loss of the "eagle". If you win, you start again with a bet of 1000 rubles, and if you lose, double your bet each time until you win. It may seem that after some time you will become a millionaire. But playing on this system, the player does not get the advantage, he just redistributes his winnings: the player rarely loses, but in large quantities, but often wins and gradually. You were unlucky, and “tails” fell out four times in a row. The probability of such an outcome is 0.5 * 0.5 * 0.5 * 0.5 = 0.0625

This is more than 6 times for 100 experiments on 4 coin flips, why couldn’t your case be one of 6? Statistics does not say that 0.0625 is not enough and you should get lucky, it says about an infinitely large series of experiments on 4 coin tossing. The law of large numbers in the theory of probability states that the empirical average (arithmetic average) of a sufficiently large final sample from a fixed distribution is close to the theoretical average (mathematical expectation) of this distribution. That is, the larger the series of experiments, the closer the results of these experiments are to the calculated probability (in our case, 0.0625). But if a finite and a small number of experiments occur, the result can be anything. In other words, immediately trying to play again on 15,000 in the same way, the next loss will still fit into the possible distribution of the results of coin flip. It is worth noting that the combination of two losses as a result of two series of 4 throws is much less. 0.0625 * 0.0625 = 0.00390625 or about 4 per 1000 experiments (from two series of 4 tosses). Such a probability is already a reason to think about the fairness of the game, but it cannot be the only evidence of its dishonesty, since such an outcome is possible.

Let's go to practice

All these examples are given not just to protect statistics, but also to help make a correct analysis of the indicators of a statistically controlled system. An example of a managed system in our case is the technical support department with 20 specialists. For ease of understanding, we assume that they are fully loaded and solve any types of problems that arise for different customers. Approximately an equal amount of time is spent on solving different types of problems. At the end of the month, the following results were obtained. They are sorted in ascending or descending form and will be the basis for the conclusions of many managers.

A place	Specialist	Total hits, pcs	Average time for one ticket, min
one	Ivanov	246	39
2	Petrov	240	40
3	Chkalov	234	41
four	Fedotov	228	42
five	Maximov	222	43
6	Korolev	222	43
7	Frolov	222	43
eight	Chernov	216	44
9	Belov	216	44
ten	Antonov	216	44
eleven	Grigoriev	216	44
12	Tkachenko	210	46
13	Kuznetsov	204	47
14	Romanov	204	47
15	Smirnov	204	47
sixteen	Vasiliev	204	47
17	Novikov	198	48
18	Yakovlev	192	50
nineteen	Popov	190	51
20	Fedorov	142	69

Suppose the head of the department decides to give out a bonus to managers in the TOP-3 in the amount of 20% of the salary and to fine 20% of three specialists with the worst results. Is it right to solve the question of motivation? The head of the department explains his decision by the desire to provide an incentive for employees to strive for better results and not be among the worst. Why were three specialists selected from the ends of the list? Perhaps because this is the favorite number of the head of the department.

What happens if you use the statistics?



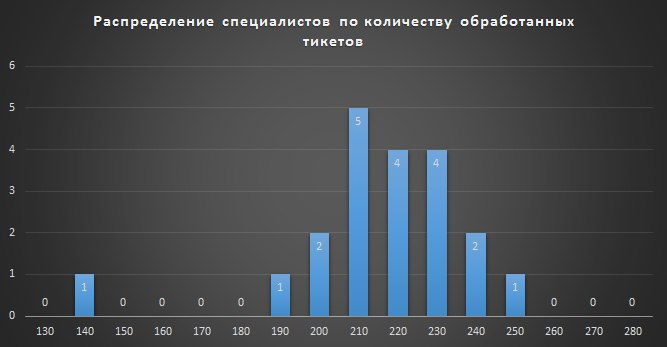
This is the distribution density of specialists in the number of processed appeals. It is well seen that 19 specialists form a sample, the indicators of which will be well described by a normal distribution.

If the observation result is the sum of many random weakly interdependent quantities, each of which makes a small contribution relative to the total sum, then with an increase in the number of terms, the distribution of the centered and normalized result tends to normal. This law of probability theory has the consequence of a wide distribution of the normal distribution, which was one of the reasons for its name.

What does this mean in terms of statistics and probability theory? 19 experts worked fine . There were many phenomena (noise, indoor temperature, mood, etc.), each of which influenced specialists to varying degrees, which led to the actual distribution of the results. Can we say that the first in the list worked better than the nineteenth, which they want to fine? Statistics in this case says that the difference in the results of their work may be due to random causes, the cumulative effect of which some people call luck. Should success or failure cause a change in employee income? In my opinion, no. As a result, the employee will not feel the connection between the effort expended and the result obtained. This will not create additional incentives to improve work efficiency.

What about the twentieth employee (Fedorov)? If we accept the hypothesis that the results of employees in our system are distributed normally, the probability of obtaining any result in such a system will be known to us. Fedorov processed 140 tickets. The probability of such an event with a normal distribution, that is, under the cumulative effect of many of the same random factors, is 1 per 10,000 experiments. We have two options: either Fedorov was terribly unlucky, or there are some special reasons (including a reluctance to work) that influenced his results.

As far as they are sensitive to the deviations of the framework in which the results of the employees will fit, everyone can choose for himself by following certain rules. According to the principle of Shuhart-Deming control charts, control boundaries are a corridor within which values ​​are at a stable (normal) state of the process.

The purpose of building a Shewhart control card is to identify the process exit points from a stable state in order to establish the reasons for the deviation that has appeared and eliminate them. Popular, thanks in large part to Deming, is the 6 sigma method.

The name of the method is based on the statistical concept of the standard deviation, denoted by the Greek letter σ. The maturity of the process in this concept is described as the percentage of the elements of the system, whose output parameters fall within 99.99966% of the density of the normal distribution. For control purposes in this method, it is important for us to understand what control limits we take. Phenomena with what probability we will be considered anomalous or in terms of control charts "emissions" of processes? The standard practice is three standard deviations from the arithmetic mean. Why 6 sigma and not 8 or 4? It is possible to multiply by three comfortably and pleasantly, but the main thing is that a really small part of the distribution remains to be within ± 3 sigma, the emission to which is worth attention. It is clear that the deviation from the average can be added both by obtaining the upper control limit and taken away to obtain the lower control limit.



Let's make a control card for the fictional results of the technical support department.



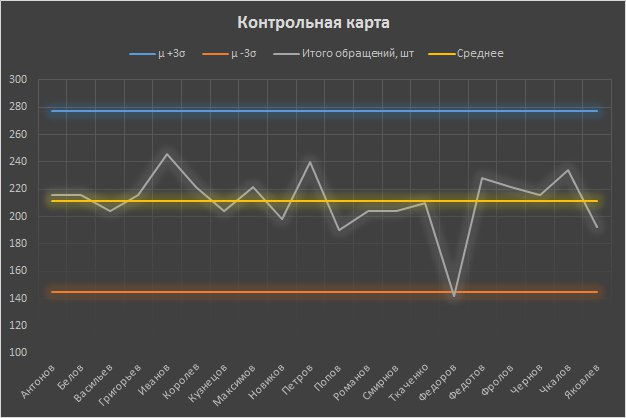
Indeed, Fedorov showed an anomalous result that did not fall into the control borders. Interviewing him, the head should find out about the reasons for this result and decide on the motivation of the employee, depending on the validity of these reasons. The results of the other employees turned out to be normally distributed, and therefore, from a statistical point of view, they were influenced by many random factors. In the event that any of the workers showed an outstanding result outside the upper control boundary, this phenomenon would also require a study on the possibility of implementation on a larger scale.

However, deciding on the motivation of employees at the end of the month is not the best solution. In the past, nothing will be changed, and the poor performance of individual employees may affect the performance of the entire department. In order to respond in time and adjust the vector of development of the system, we need more control charts. Imagine that we have them for each employee and we record the observations daily.

Let's look at the Fedorov control card, but first let us say a little about the signs of special variability of the process, signaling a violation of the stability (controllability) of the process and the appearance of a special reason for this variability:

• exit of points beyond the upper or lower border of the control card
• 7 or more points in a row lie on one side of the middle line.
• more than 6 points monotonously increase or decrease

There are other signs. There is no established generally accepted set of additional rules for reading control cards, so it is recommended to use the Shewhart rule first (go beyond points), and introduce all the others as you gain experience if necessary.



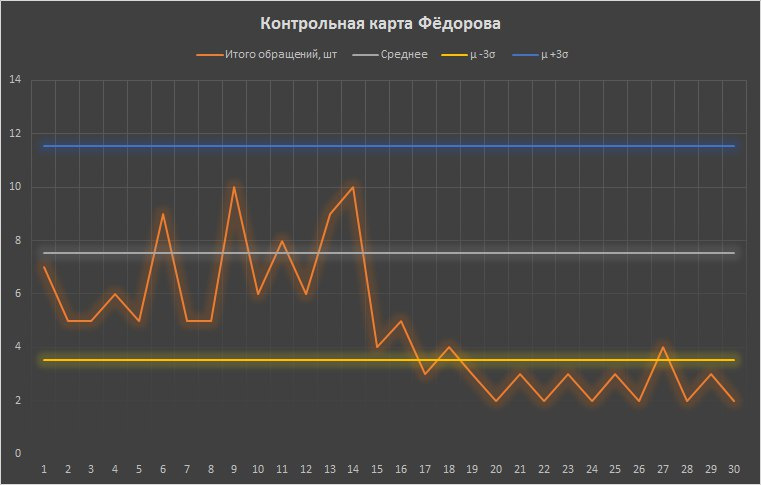
Notice that Fedorov's work results changed, it was possible not only at the end of the month. Already on the 17th, there was an ejection of the indicator beyond the control limits. It was at this moment that the head of the department had to notice the signal and find out the reasons for this anomaly.

In general, this is a topic of quality management. Its purpose is to ensure the stability (controllability) of any processes: the sales process, personnel management, the provision of services or production. We give an example already with real numbers. As a cloud provider, we must ensure the availability of our SLA services of at least 99.95% . That is, a certain infrastructure (for example, a virtual machine with certain characteristics) or a service (for example, a virtual desktop) may be unavailable for a client for no more than 22 minutes for the entire month. To ensure such reliability and stability of exits from the process of providing services, the cloud provider builds a stable system that is monitored with a much greater frequency than in the example earlier. Such a system is based on enterprise-level equipment located in several Tier III data centers connected by a high-availability optical ring with duplicated channels, and, of course, 24x7 technical support. The cloud provider business is one of the clearest examples when the quality of services depends on the quality of computer systems and organization personnel.

If you like the topic of statistical process management, we highly recommend reading Edwards Deming's book “Overcoming the Crisis: A New Paradigm of Managing People, Systems, and Processes”. Deming first visited war-torn and backward Japan in 1946. His lectures on statistical quality control methods were perceived by top executives of Japanese companies. The need to study and implement statistical control methods was realized, and in Japan a process of mass training of managers was organized. The further development of these methods led to the creation of the Toyota Tao system and Kaizen philosophy. Many consider these methods to be the cause of the “Japanese economic miracle”, which brought the country into economic leaders. Here are a couple of quotes from the book “Overcoming the Crisis,” which prompted us to write this article.

"Ranking people belonging to the system (from outstanding to worst) is contrary to scientific logic and destructive as a politician."

“The manager should be able, using calculations, if relevant data are available, or on the basis of judgment, when there are no such data, to distinguish those workers who are outside the system for the worse and for the better, and thus require either special assistance , or should be highlighted and encouraged in one form or another. "