Game control models in the context of incomplete information

In collaboration with Yulia Filimonova.

Introduction

Imagine that you fly such a whole winner to the base, there are no bombs, and nothing foreshadows trouble ...

And here, say, a mound of fog / clouds appears unexpectedly, or, which is somewhat worse, this is ... And you are welcome, but only as a goal:

# to attack - but how to do it with a mathematical bias now and we will understand.
And in general there are many cases when it is necessary to evade unexpected interference / obstacles, our Law , as they say in Yandex , for example.

Reservation for mathematicians. , . : - , , , .

Part one - the model in the "simple movements"

Simple movements are not what pops sing about, but the simplest model of a dynamic object, expressed by the following differential model:

$$$$ display $$ \ dot x = u, \ x (t_0) = x_0, $$ display $$

Where$$ $ inline $ x (t) \ in R ^ n \ u \ in P \ subset R ^ n $ inline $ , -management is limited$$ $ inline $ P: | u | <c_u $ inline $ (which is logical, because the speed is not infinite), but$$ $ inline $ r ^ n $ inline $ -$$ $ inline $ n $ inline $ -dimensional Euclidean space (for our example, as you can see, two-dimensional is quite enough). Lots of$$ $ inline $ M $ inline $ - our base, i.e. here we want to return safe and sound - located at the point$$ $ inline $ x_1 $ inline $ .

What does this give us? If we integrate the equation, then we get the trajectory of movement - a straight line$$ $ inline $ x (t) = ut + C $ inline $ , that is, where control is directed, there we go. So, in the absence of interference, the control vector$$ $ inline $ u $ inline $ aligned with the motion vector$$ $ inline $ x_1 - x_0 $ inline $ .

Plus of this model is in its extreme simplicity for analysis, minus - it models only non-invasive movements, but this is not very scary since the simulation of inertial movements will look (simplified) like:

$$$$ display $$ \ ddot x = u \ Rightarrow \ left \ {\ begin {array} {rcl} \ dot x_1 & = & x_2 \\ \ dot x_2 & = & u. \ end {array} \ right. $$ display $$

and we will pass to models of the corresponding type a bit later.

The described model reflects our dynamic capabilities. Add an opponent to it$$ $ inline $ v $ inline $ which in every possible way tries to prevent us:

$$$$ display $$ \ dot x = u - v, \, x (t_0) = x_0, \, \ exists T: x (T) \ in M, \, \ forall t <T: x (t) \ notin N, \, u \ in P \ subset R ^ n, \, v \ in Q \ subset R ^ n $$ display $$

Here is similarly limited control.$$ $ inline $ Q: | v | <c_v $ inline $ .

At the same time, we do not know in advance where the enemy was hiding, but he, at the same time, knows everything and waits for himself while we fly closer, so that with the help of our management$$ $ inline $ v $ inline $ get us many$$ $ inline $ n $ inline $ .

Since our goal is to get to$$ $ inline $ M $ inline $ guaranteed to avoid$$ $ inline $ n $ inline $ , and we need to know from what, in fact, we shy away, then sooner or later we will find a hindrance. In the case of inertialess motion, we may not know anything about it until the penultimate time point, since in this case we can always direct the velocity vector (and, accordingly, the trajectory) away from the disturbance.

At the same time, as you can see, an obstacle of the << mountain >> type is not the most terrible situation, since it is motionless, although it is a big obstacle - it is worse if the enemy is mobile, therefore you need to discuss a couple more points:

• to be able to evade, we must have greater dynamic capabilities than the enemy, otherwise sooner or later we will be caught, that is,$$ $ inline $ Q $ inline $ in a sense should be less$$ $ inline $ P $ inline $ ;
• let the set of interference, which is controlled by the enemy, is convex, otherwise, if we use the evasion strategy normal to the set of interference$$ $ inline $ n $ inline $ - it is possible and not to evade.

Using the above heuristic reasoning, let's see how you can solve the above problem under the following conditions in space$$ $ inline $ R ^ 2 $ inline $ :

$$$$ display $$ \ begin {array} {rcl} \ dot {x} _1 & = & u_1 - v_1, \\ \ dot {x} _2 & = & u_2 - v_2. \ end {array} $$ display $$

Here$$ $ inline $ x_1, \ x_2 $ inline $ - object coordinates$$ $ inline $ x $ inline $ on surface,$$ $ inline $ x (t) = [x_1 (t), \ x_2 (t)] ^ {T} \ in \ mathbb {R} ^ 2. $ inline $

Let the object start moving from a point$$ $ inline $ x (t_0) = [3, \ 4] ^ {T} \ in \ mathbb {R} ^ 2. $ inline $
Control restrictions$$ $ inline $ u (t), \ v (t) $ inline $ have a look

• $$$ inline $ u (t) \ in P \ subset \ mathbb {R} ^ 2, \ P = S_ {1} ([0, \ 0] ^ {T}) $ inline $ - circle of radius 1;
• $$$ inline $ v (t) \ in Q \ subset \ mathbb {R} ^ 2, \ Q = S_ {0.9} ([0, \ 0] ^ {T}) $ inline $ - circle of radius 0.9.

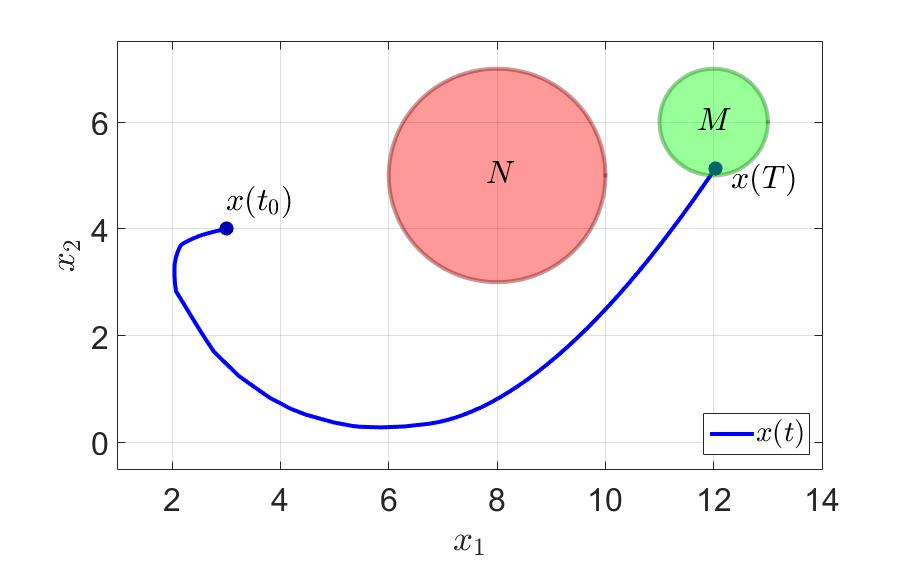
The first player seeks to translate the trajectory of the system for a finite time to a terminal set$$ $ inline $ M = S_ {1} ([12, \ 6] ^ {T}) $ inline $ - circle of radius 1 centered at$$ $ inline $ [12, \ 6] ^ {T} $ inline $ while avoiding a lot of interference$$ $ inline $ N = S_ {2} ([8, \ 5] ^ {T}) $ inline $ - a circle of radius 2 with the center at the point$$ $ inline $ [8, \ 5] ^ {T} $ inline $ .

Time to successful completion of the game the first player$$ $ inline $ T = 36.0 $ inline $ .

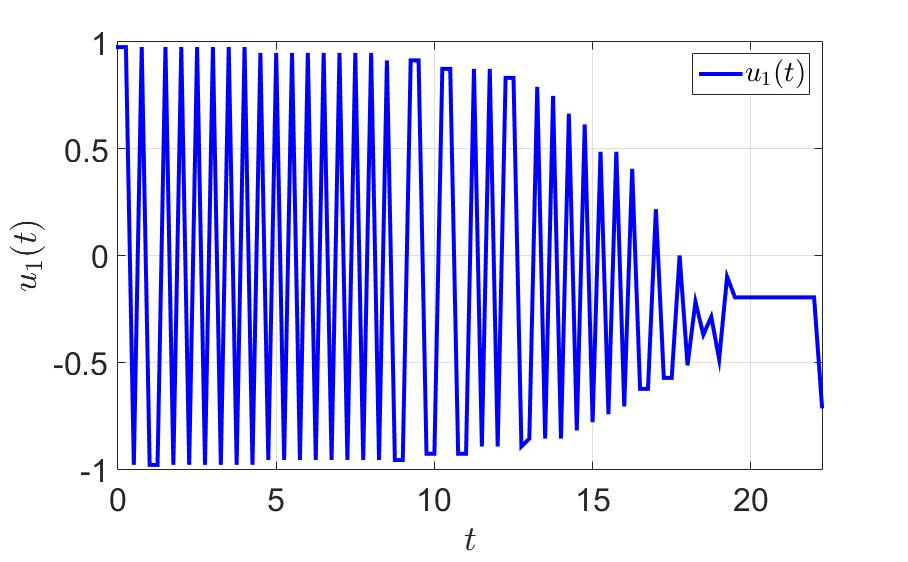
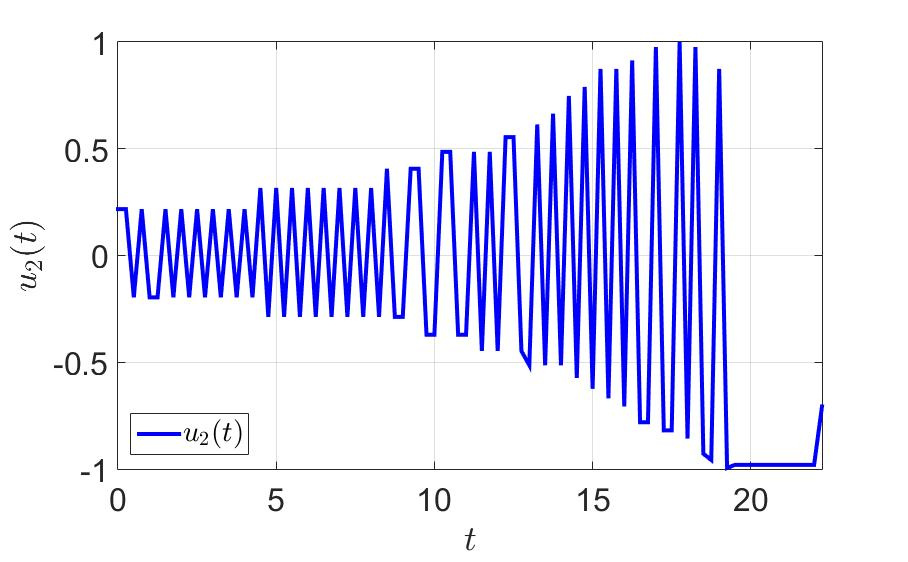
The trajectory of the system and the control components of the first player are shown in the following figures.

The trajectory of the system.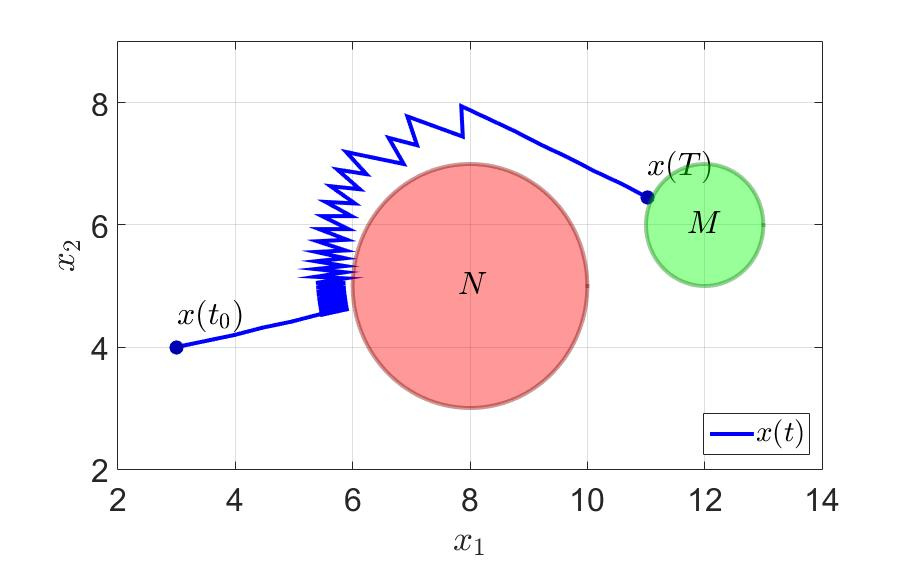
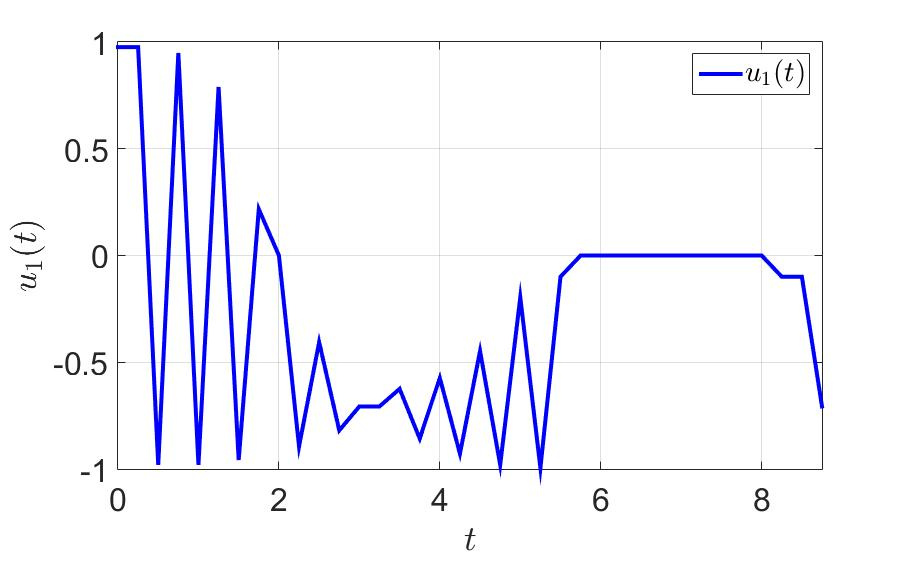
The dependence of the first control component on time.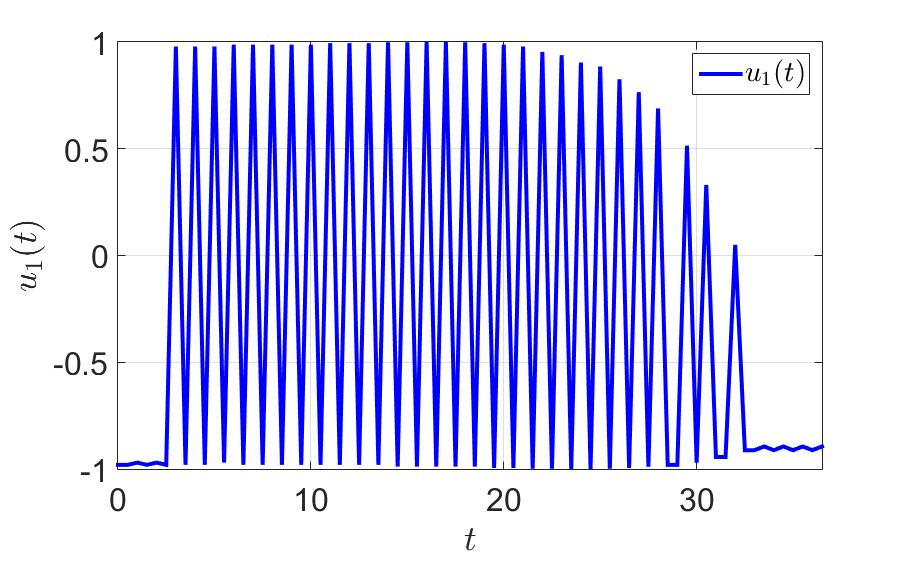
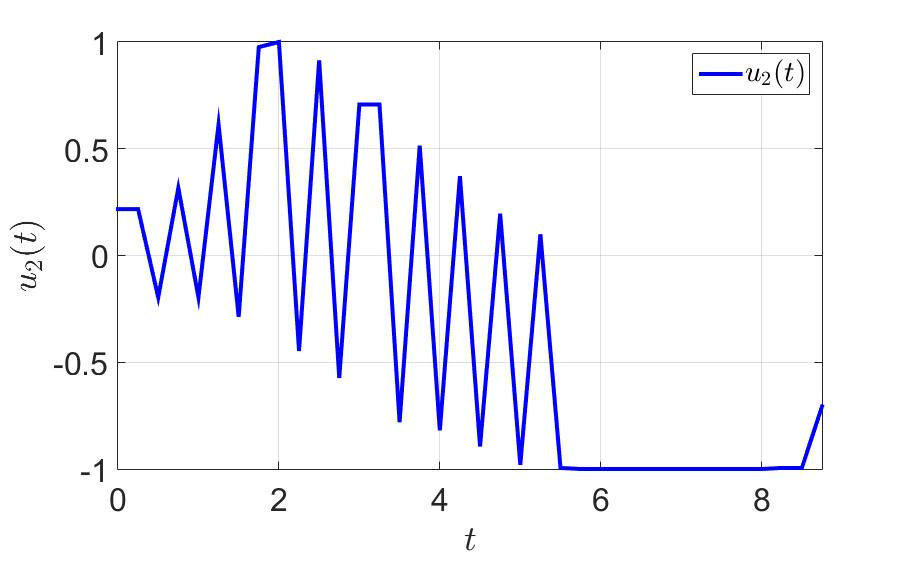
Dependence of the second control component on time.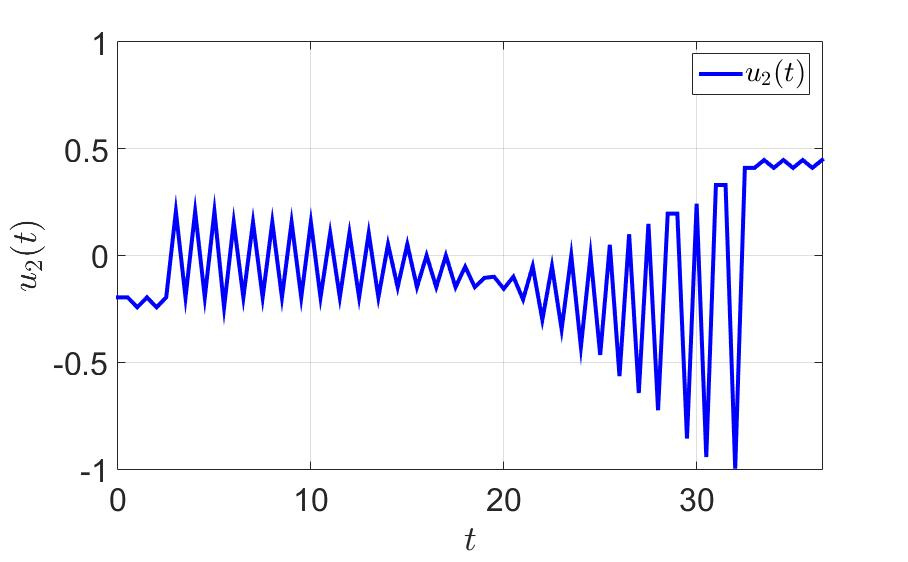

This approach obviously has several drawbacks, namely:

• a large number of switchings, which is bad from a practical point of view, since jerks between extreme values ​​put a substantial load on the controls;
• as a result, instead of flying to the target, we spend time on wandering, associated with avoiding interference and aiming at the terminal set;
• it is not clear what to do if we fly up to the hindrance strictly along the normal: evasion will be carried out to the same point from which we were led a step before that, that is, the algorithm can loop;
• It is not clear what to do with inertial objects, since heuristics, of course, are good, but the reality is somewhat more complicated.

Part two - the model is still in “simple movements”, but the number of switching is reduced

Due to the fact that the model is simple and allows us to move on a plane from any point to any point (this will continue to be a significant assumption, but for now just take a note), nothing prevents us from thinking as follows.

Let's think one step forward: if our system was first aimed at the target, and at the next step, the beginnings will dodge, then we can find the point where the system will come in two steps, and direct it at once as an intermediate goal. Can we? According to our assumption - YES.

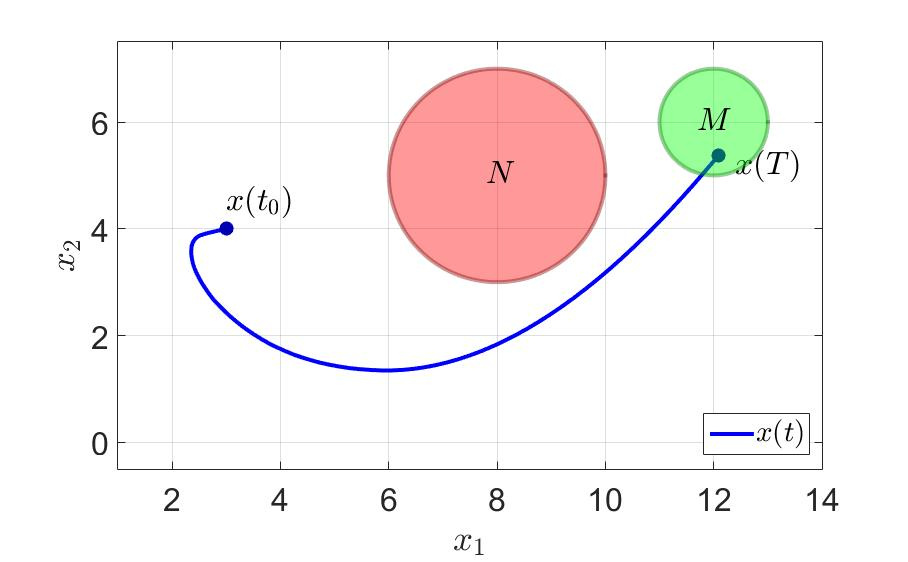
On the same example, let's see what happens. The time for the successful completion of the game by the first player has decreased almost three times since$$ $ inline $ T = 36.0 $ inline $ before$$ $ inline $ T = 11.5 $ inline $ . The number of switches has also decreased dramatically. Take note - to think at least one step forward effectively and generally good for health .

The trajectory of the system and control components of the first player are shown in the following figures.

The trajectory of the system.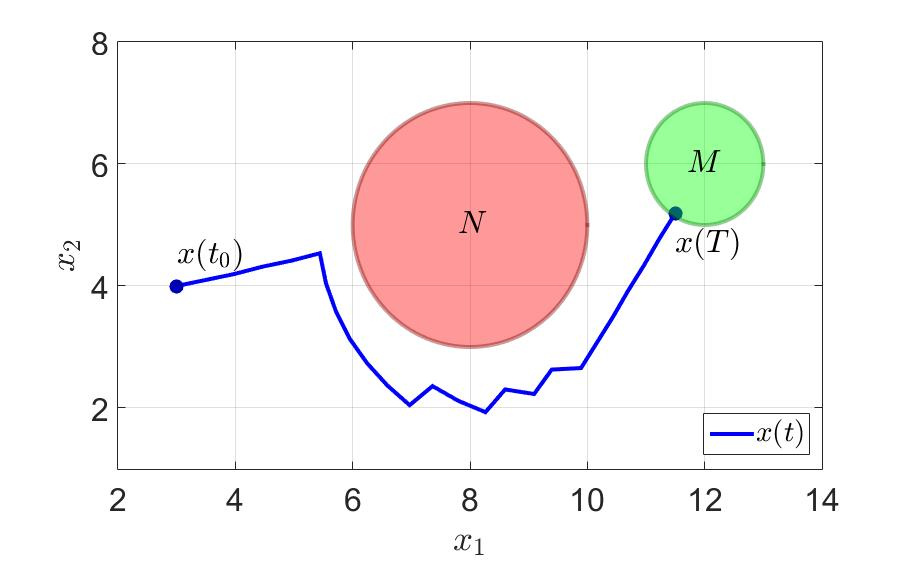
The dependence of the first control component on time.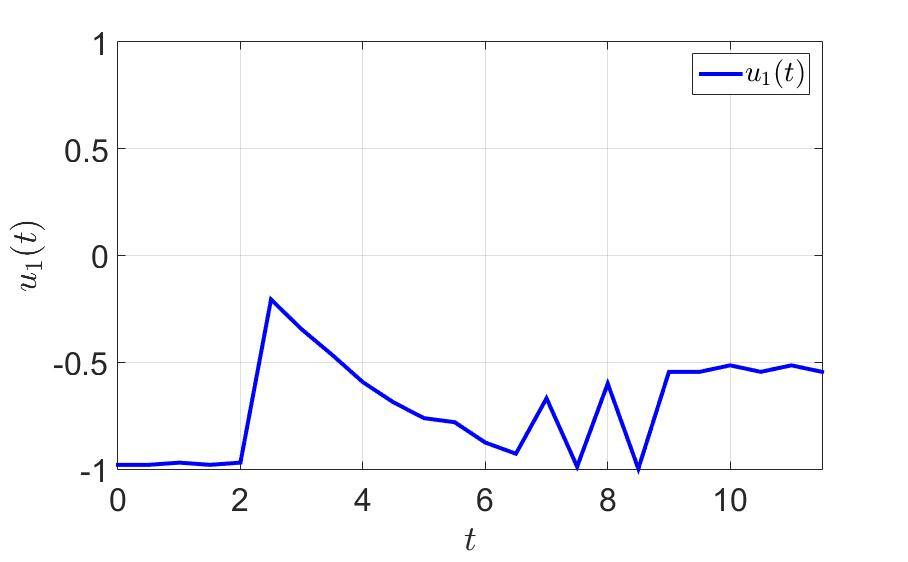
Dependence of the second control component on time.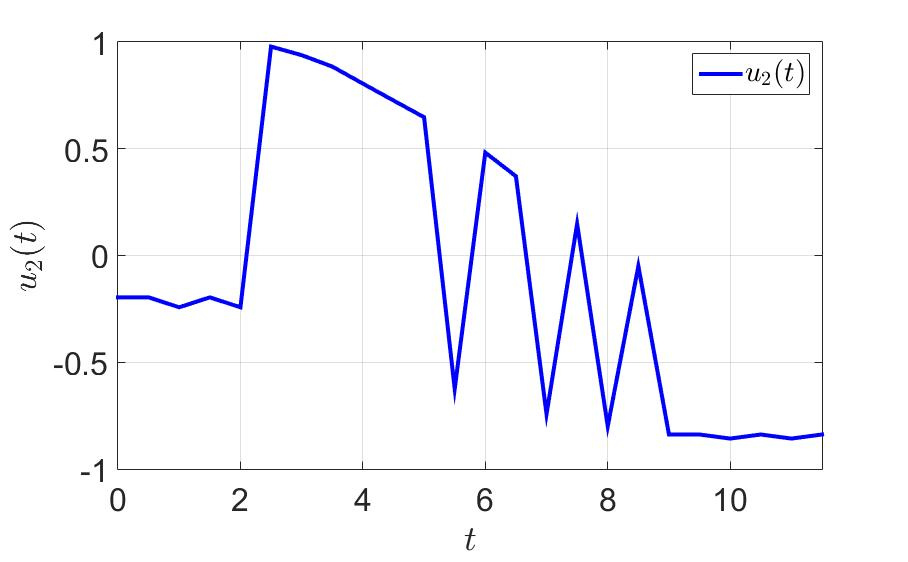

Part three - the model is still in “simple movements”, but now we are solving the issue with an approximation of “normal”

Since we are able to evade one set at one time, then nothing prevents us from building an additional set so that, evading it, we (perhaps with grinding time step) guaranteed in two steps get to a point different from that in which we are now. And we will do this as follows:

Constructing an additional avoidance set for the trajectory.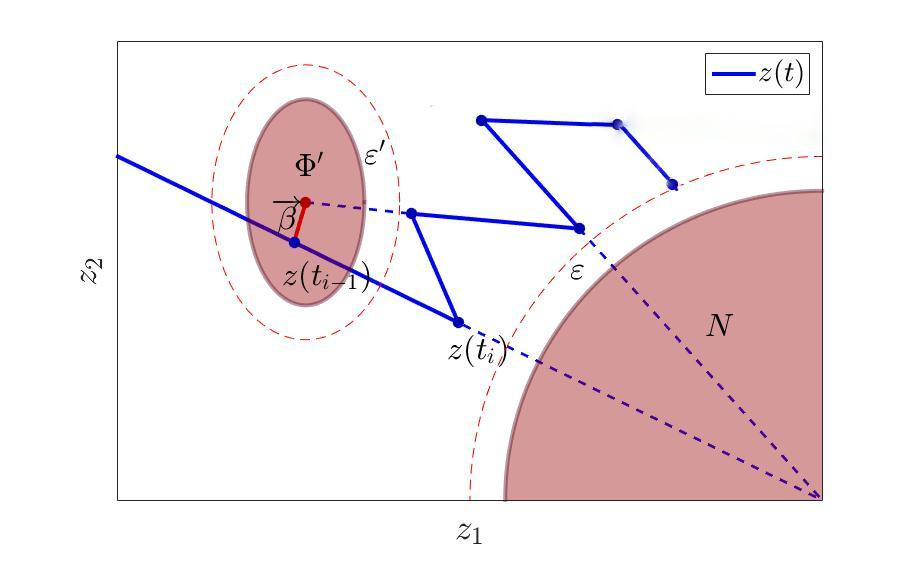

That is, we simply construct an additional set, from which we will shy away, containing the “problem” point not as a center, but with a certain displacement, as in the figure.

Part Four - Mathematical Basis

In order to build controls of inertial objects, it is necessary to immerse yourself in the theory, since simple heuristic reasoning in this case stops working and, accordingly, it is necessary to choose the theoretical basis for the solution. If you have hard laziness there is not enough time, then the section can be skipped and immediately use the results, but we are interested in looking further.

As a basis, we will use the theory of differential games that were developed in our country by Lev Semenovich Pontryagin [1] (if you don’t know who he is, be sure to read, I don’t do a Person with a capital letter) and Krasovsky Nikolai Nikolayevich [2] .

To solve, we need two sets:

• where you can get the first player - the set of reachability of the first player;
• from where you can complete the pursuit of the second player first.
  And also the way to build them, implemented in practice.

With the first set, in the absence of interference, everything is more or less clear if we can build it in such a way as to include a finite set$$ $ inline $ M $ inline $ - then the game will end successfully, we can not - then the game just can not be completed. It is built in theory as follows - for each point starting from the initial$$ $ inline $ x_0 $ inline $ by enumerating all the available controls, we build a set into which we can get through$$ $ inline $ \ Delta t $ inline $ after which the operation is repeated. It looks quite difficult, but for convex sets and linear systems everything can be radically simplified using the apparatus of convex analysis — supporting functions and entering the corresponding grids [4]. The construction of such a set solves the task of pointing the first player, let's call it - task A.
Targeting $ M $ in the absence of interference .

As for the second set - the sets from which the second player can catch us and from which we need to evade, here it is somewhat more difficult - watch your fingers:

• on the one hand, if we are “approaching” the enemy, then, in view of the superiority of our capabilities, the further we are from him, the more likely we are to catch, then this will have to be given a strict explanation;
• on the other hand, if we are “moving away” from the enemy, then due to the same superiority of ours, the enemy will not be able to catch us in any case.

That is, what turns out to be a set from which we shy away should be, on the one hand, large (when approaching), and with the side arc (when moving away) it can be barely larger than that from which it is necessary to shy away?
Evasion of many$$ $ inline $ n $ inline $ .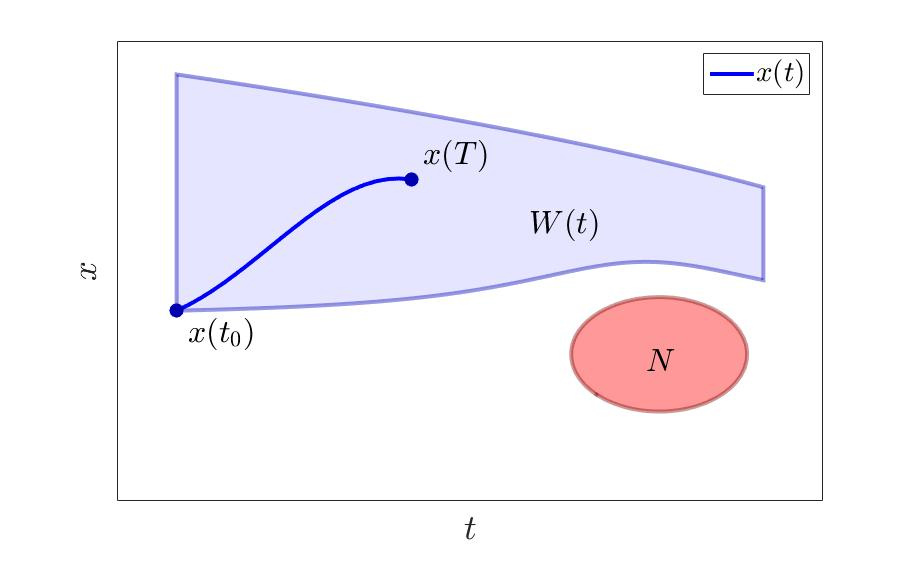

Coincidence? Contradiction? I do not think. Like Doc in “Back to the Future” with his “space-time continuum”, we recall that we have another variable — time and we will interpret the terms “approaching” and “moving away” given in quotation marks as the behavior of the system along the trajectory, which is not always coincides with rectilinear motion and is certainly not characterized by distance in Euclidean space. But the time of movement to a specific point of the concept of "far-close" and "approaching-moving away" is characterized very well.

In this case, let's build the evasion control not from the set from which we need to evade.$$ $ inline $ n $ inline $ , and from the set to which it is converted (and it will decrease due to the superiority of the first player) by the time it approaches the corresponding time interval in the set$$ $ inline $ n $ inline $ - i.e. let's build a funnel directed towards the first player with its narrow side and we will start from it. Building such a set at each moment of the game and evading it will solve the problem of evading the first player, let's call it - task B.

Accordingly, the general management is the management of the first player so that at each time point he solves only one of these subtasks.

We now formalize the movement of our object.$$ $ inline $ x $ inline $ , at$$ $ inline $ x $ inline $ - dimensional Euclidean space$$ $ inline $ \ mathbb {R} ^ n $ inline $ following system of differential equations:

$$$$ display $$ \ dot {x} = A x + B u - C v, $$ display $$

Where$$ $ inline $ x \ in \ mathbb {R} ^ n, \ u \ in P \ subset \ mathbb {R} ^ p, \ v \ in Q \ subset \ mathbb {R} ^ q $ inline $ ;$$ $ inline $ P, \ Q $ inline $ - convex compacts from Euclidean spaces$$ $ inline $ \ mathbb {R} ^ p, \ \ mathbb {R} ^ q $ inline $ ;$$ $ inline $ A, \ B, \ C $ inline $ - constant matrices$$ $ inline $ A \ in \ mathbb {R} ^ {n \ times n}, \ B \ in \ mathbb {R} ^ {n \ times p}, \ C \ in \ mathbb {R} ^ {n \ times q} $ inline $ that ensures the existence, uniqueness, and extendability of all$$ $ inline $ t \ ge t_0 $ inline $ solving the Cauchy problem .

Vector$$ $ inline $ u $ inline $ is at the disposal of the first player, vector$$ $ inline $ v $ inline $ is at the disposal of the second player.

The movement starts at$$ $ inline $ t = t_0 $ inline $ from the initial state$$ $ inline $ (x_0, \ t_0) $ inline $ and proceeds under the influence of Lebesgue measurable functions$$ $ inline $ u (t) \ in P, \ v (t) \ in Q $ inline $ .

AT$$ $ inline $ \ mathbb {R} ^ n $ inline $ selected some non-empty convex closed sets$$ $ inline $ M $ inline $ and$$ $ inline $ n $ inline $ . Lots of$$ $ inline $ M $ inline $ is the terminal set of the first player. The goal of the first player is to achieve the turn-on.$$ $ inline $ x (t_1) \ in M ​​$ inline $ with some$$ $ inline $ t_1 \ ge t_0 $ inline $ . Lots of$$ $ inline $ n $ inline $ is the second player's terminal set and the first player's interference set. The goal of the second player is to achieve the turn-on.$$ $ inline $ x (t_1 ') \ in N $ inline $ with some$$ $ inline $ t_1 '\ ge t_0 $ inline $ . At the time of the first hit point$$ $ inline $ x (t) $ inline $ on$$ $ inline $ n $ inline $ The game is considered to be a successfully completed second player. Additional task of the first player - to avoid hitting the point$$ $ inline $ x (t) $ inline $ on$$ $ inline $ n $ inline $ .

The game is considered to be successfully completed by the first player at the time of the first hit point.$$ $ inline $ x (t) $ inline $ on$$ $ inline $ M $ inline $ provided that for all previous time points the point$$ $ inline $ x (t) $ inline $ never hit on$$ $ inline $ n $ inline $ . Thus, the goals of the players do not match, and the point$$ $ inline $ x (t) $ inline $ is under the influence of opposing directorates$$ $ inline $ u (t), \ v (t) $ inline $ .

We will separately consider the differential game from the point of view of the first and second players.
A: It is assumed that the first player knows:

1. dynamic capabilities of the conflicting object$$ $ inline $ x $ inline $ i.e. matrices$$ $ inline $ A, \ B, \ C $ inline $ , sets$$ $ inline $ P, \ Q $ inline $ ;
2. initial state of the game$$ $ inline $ (x_0, t_0) $ inline $ ;

It is also assumed that the first player is able to detect many$$ $ inline $ n $ inline $ no later than the time$$ $ inline $ \ Theta> 0 $ inline $ whose value is defined below.

Define first player strategy$$ $ inline $ u (t) = U (x_0, t_0, v_t (\ cdot)) $ inline $ as a mapping defined on a set of arbitrary measurable functions$$ $ inline $ v (t) \ in Q, \ t \ ge t_0 $ inline $ , and possessing the following property: for arbitrary measurable$$ $ inline $ v (t) \ in Q, \ t \ ge t_0 $ inline $ function$$ $ inline $ u (t) = U (x_0, t_0, v_t (\ cdot)) $ inline $ measurable by$$ $ inline $ t $ inline $ and$$ $ inline $ u (t) \ in P $ inline $ .

Task A: Find the initial states$$ $ inline $ (x_0, t_0) $ inline $ , for which the first player has such a strategy that it provides the end of the game for an arbitrary measurable$$ $ inline $ v \ in Q $ inline $ no later than some final moment. Such states$$ $ inline $ (x_0, t_0) $ inline $ will be called solutions to A.

B: The second player has full information about the game.
Define second player strategy$$ $ inline $ v (t) = V (x_0, t_0, u_t (\ cdot)) $ inline $ as a mapping defined on a set of arbitrary measurable functions$$ $ inline $ u (t) \ in P, \ t \ ge t_0 $ inline $ , and possessing the following property: for arbitrary measurable$$ $ inline $ u (t) \ in P, \ t \ ge t_0 $ inline $ function$$ $ inline $ v (t) = V (x_0, t_0, u_t (\ cdot)) $ inline $ measurable by$$ $ inline $ t $ inline $ and$$ $ inline $ v (t) \ in Q $ inline $ .

Task B: Find the initial states$$ $ inline $ (x_0, t_0) $ inline $ for which the second player has such a strategy that it provides the end of the game for an arbitrary measurable$$ $ inline $ u \ in P $ inline $ no later than some final moment. Such states$$ $ inline $ (x_0, t_0) $ inline $ will be called solutions of problem B.

We will assume that$$ $ inline $ M = M ^ 1 + M ^ 2 $ inline $ where$$ $ inline $ M ^ 1 $ inline $ - linear subspace of space$$ $ inline $ \ mathbb {R} ^ n $ inline $ ,$$ $ inline $ M ^ 2 $ inline $ - convex compact,$$ $ inline $ M ^ 2 \ subset L ^ 1, \ L ^ 1 \ oplus M ^ 1 = \ mathbb {R} ^ n $ inline $ . Similarly$$ $ inline $ N = N ^ 1 + N ^ 2 $ inline $ where$$ $ inline $ N ^ 1 $ inline $ - linear subspace of space$$ $ inline $ \ mathbb {R} ^ n $ inline $ ,$$ $ inline $ N ^ 2 $ inline $ - convex compact,$$ $ inline $ N ^ 2 \ subset L ^ 1, \ L ^ 1 \ oplus N ^ 1 = \ mathbb {R} ^ n $ inline $ . Wherein$$ $ inline $ \ pi $ inline $ - orthogonal projection operator of$$ $ inline $ \ mathbb {R} ^ n $ inline $ at$$ $ inline $ L ^ 1 $ inline $ ,$$ $ inline $ \ pi \ in \ mathbb {R} ^ {\ nu \ times n} $ inline $ . These constructions are necessary in order to take into account that the game in our case (and in the presence of inertial objects, this is so) is conducted in a space of lower dimension than the dimension of the system of differential equations.

Subsection 4.1. A sufficient condition for the solvability of the problem of evading the first player from the set$$ $ inline $ n $ inline $

Consider task B - the pursuit problem by the second player of the first one and construct for it a set of points from which the given problem will have a solution. So, for this type of problem, Pontryagin invented a method for constructing the desired set — alternating sum —$$ $ inline $ w (t) $ inline $ [3], [5]. So the alternated sum is not only a convex compact, so also$$ $ inline $ v $ inline $ -stable (i.e., it allows us to build the strategies of the second player we need), and also ensures that the saddle point of the small game exists [6, p. 56] (which means that the game is solvable in principle) —that is all at once.

From [6, p. 69 - Theorem 17.1], it follows that under these conditions we can use the theorem on the alternative:

For any starting position$$ $ inline $ (t_0, x_0) $ inline $ and selected$$ $ inline $ \ bar T \ ge t_0 $ inline $ one of two statements is true:
1) Either there is a strategy$$ $ inline $ \ bar {v} $ inline $ that for all movements$$ $ inline $ x (t) = x (t, t_0, x_0, \ bar {v}) $ inline $ will provide a meeting$$ $ inline $ \ {\ tau, x (\ tau) \} \ in N $ inline $ in finite time$$ $ inline $ \ tau <\ bar {T} $ inline $ . That is, in the class of positional strategies of the second player the pursuit problem is solvable (problem B) .
2) Or, otherwise, there is a strategy$$ $ inline $ \ bar {u} $ inline $ that for all movements$$ $ inline $ x (t) = x (t, t_0, x_0, \ bar {u}) $ inline $ , will provide evasion of many$$ $ inline $ \ epsilon $ inline $ -circuits of the set $ N $ up to the point in time$$ $ inline $ \ bar {T} $ inline $ . That is, in the class of positional strategies of the first player, the evasion problem is solvable (problem A) .

In this case, in view of$$ $ inline $ v $ inline $ -stability of the set$$ $ inline $ w (t) $ inline $ on the basis of [6, p. 62 - Theorem 15.1] we obtain the condition:

$$$$ display $$ \ forall t \ in [t_0, \ bar T]: x (t_0) \ notin W (t) $$ display $$

is a sufficient condition for solving the problem of evading the first player from the initial position$$ $ inline $ (t_0, x_0) $ inline $ from$$ $ inline $ \ epsilon $ inline $ - neighborhood of the set$$ $ inline $ n $ inline $ for a time$$ $ inline $ \ bar T $ inline $ .

If the resources of the first player are determined by the set$$ $ inline $ P $ inline $ exceed the resources of the second player, defined by sets$$ $ inline $ Q $ inline $ and$$ $ inline $ n $ inline $ , then there is such a time$$ $ inline $ \ Theta $ inline $ , what$$ $ inline $ W (\ Theta) = \ emptyset $ inline $ .
Existence of the moment$$ $ inline $ t $ inline $ which is enabled$$ $ inline $ x (t) \ in W (t) $ inline $ , ensures the solvability of problem B in a time out of range$$ $ inline $ [t, t + \ Theta] $ inline $ .

That is, you can build a strategy$$ $ inline $ u (x_0, t_0, x (t)) $ inline $ satisfying the condition:

$$$$ display $$ \ forall \ tau \ in [t, t + \ Theta]: x (\ tau, u (x_0, t_0, x (\ tau))) \ notin W (\ tau). $$ display $ $

Consequently, in order to ensure deviation from the set$$ $ inline $ n $ inline $ , you need to check the above condition as for the current point in time$$ $ inline $ t $ inline $ and for all subsequent time points to the depth$$ $ inline $ t + \ Theta $ inline $ .

Lots of$$ $ inline $ \ Phi (\ Theta, t) $ inline $ built as:

$$

$$\Phi(\Theta,t) = \bigcup_{\tau\in[t,t+\Theta]}W(\tau),$$

$$t$t$, . - , ( ), , .

, , , : 5, 2, -- 1, 4. .

$$M$M$.$$M$M$ :

$$

$$\exists T: z(t_0) \in \bar{W}(T).$$

4.2.

$$N$N$,$$Θ$\Theta$ . ,$$ωK$\omega_K$$$[t0, T]$[t_0,\ T]$ , ,$$s$s$ :

$$

$$s = \frac{\Theta}{\Delta_{\omega_K}}.$$

( )$$τ+ΔωK$\tau + \Delta_{\omega_K}$ :

$$

$$x(\tau) \in \Delta_{\omega_K} \pi e^{\tau A}CQ + W(\tau),\, \tau\in[t,t+\Theta].$$

$$τ$\tau$,$$τ+ΔωK$\tau + \Delta_{\omega_K}$ .
, , .

:

1. $$M$M$:

   
   

   $$

   $$\forall T: \Phi( T, \tau) \cap M \neq \emptyset;$$
   
   

   " " ;

   
   
2. $$Φ(T,τ)$\Phi( T, \tau)$, — :
   

   $$

   $$x(t_0)\notin \Phi( T, \tau),$$
   

   , .

   
   
   
   

   $$N$N$$$M$M$.

   
   

   , ,$$x0:x0∉Φ(Θ,τ)$x_0: x_0 \notin \Phi(\Theta,\tau)$ , , ,$$x(t)$x(t)$$$Φ(Θ,τ)$\Phi(\Theta,\tau)$$$ϵ$\epsilon$ , .

   
   

   , , , .

   
   

   , , , [6, . 69],$$N$N$ :

   
   

   $$

   $$U(\theta - t_i, x(\theta - t_i)) \in \underset{u \in P} {\mathrm{argmax}} \left\{ \pi u,\tilde{\psi_i}(x(\theta - t_i)) \right\},$$
   
   

   Where

   
   

   $$

   $$\tilde{\psi_i}(x(\theta-t_i))\in \underset{\psi \in S_1(0)} {\mathrm{argmin}} \left\{ c(\Phi(\Theta,\tau),\psi)-(\pi x(\theta-t_i),\psi) \right\}.$$
   
   

   15.2 [6, . 65], , ,$$x(t)$x(t)$$$Φ(Θ,τ)$\Phi(\Theta,\tau)$ ,$$0$0$ .

   
   

   $$M$M$. -$$N$N$ ,$$x(t0)$x(t_0)$ , :

   
   

   $$

   $$U(\theta-t_i,x(\theta-t_i))\in \underset{u \in P}{\mathrm{argmin}}(\pi u,\tilde{\psi_i}(x(\theta-t_i))).$$
   
   

   -- :

   
   
   • $$T$T$, ;
   • $$ti$t_i$,$$i=¯0,T$i=\overline{0,T}$ .
   
   

   :

   
   

   $$

   $$\pi (x(t_i) + P) \cap \Phi(\Theta,\tau)$$
   
   
   • $$x(ti)$x(t_i)$$$Φ(Θ,ti)$\Phi(\Theta,t_i)$, ;
   
   
   • .
   
   

   , , ..$$w(ti+1)∉W(T)$w(t_{i+1})\notin W(T)$ where$$T$T$ ,$$W(T)$W(T)$ — . ..$$W(Tj)$W(T^j)$$$Tj$T^j$ ,$$j$j$ - .

   
   

   ,$$M$M$ , ,$$N$N$ , .

   
   

   $$N$N$— , ,$$N$N$ . , .

   
   

   $$

   $$\bar{T}_{min} = T$$
   
   

   — ,$$ˉTmax$\bar{T}_{max}$ , .

   
   

   —

   
   

   , , . — " ", . .

   
   

   :

   
   

   $$

   $$\begin{array}{rcl} \dot{x}_1 &=& x_3,\\ \dot{x}_2 &=& x_4,\\ \dot{x}_3 &=& u_1 - v_1,\\ \dot{x}_4 &=& u_2 - v_2. \end{array}$$
   
   

   Here$$x1, x2$x_1,\ x_2$ —$$ $ inline $ x $ inline $ ,$$x3, x4$x_3,\ x_4$ — ,$$x(t)=[x1(t), x2(t), x3(t), x4(t)]T∈R4;$x(t) = [x_1(t),\ x_2(t),\ x_3(t),\ x_4(t)]^{T} \in \mathbb{R}^4;$
   $$x(t0)=[3, 4, 0, 0]T∈R4.$x(t_0) = [3,\ 4,\ 0,\ 0]^{T} \in \mathbb{R}^4.$

   
   

   $$u(t), v(t)$u(t),\ v(t)$

   
   

   $$

   $$u(t) = [u_1(t),\ u_2(t)]^{T} \in P \subset \mathbb{R}^2,\ P = S_{1} ([0,\ 0]^{T}),$$
   
   

   $$

   $$v(t) = [v_1(t),\ v_2(t)]^{T} \in Q \subset \mathbb{R}^2,\ Q = S_{0.9} ([0,\ 0]^{T}).$$
   
   
   
   

   $$

   $$M = S_{1}([12,\ 6]^{T}),$$
   
   
   
   

   $$

   $$N = S_{2}([8,\ 5]^{T}).$$
   
   

   ,

   
   

   $$

   $$T = 22,30.$$
   
   

   .

   
   

   .
   

   
   

   .
   

   
   

   .
   

   
   

   , :

   
   

   $$

   $$T = 8,80$$
   
   

   .

   
   

   .
   

   
   

   .
   

   
   

   .
   

   
   

   , , , .

   
   

   findings

   
   

   ( , , ), — "" "" , (. .. c, .. .. ), .

   
   

   : GitHub

   
   

   , 19 , , C++ , , .. . .

   
   

   , .. , , , .. " " .

   
   

   .

   
   

   UPD: technic93 , (. ).

   
   
   
   

   [1] .. . . , , », , 1983

   
   

   [2] .. : , , , 1968

   
   

   [3] .. , , , 1990

   
   

   [4] .. , .. , .. . , , 2007

   
   

   [5] .., .., .. , , 2007

   
   

   [6] .., .. , , , 1974

   
   

   [7] .., . , , , 1972

   
   

   [8] .., .., .., .. , , , 1969

   
   

   ( jul305a@gmail.com )