Nelder-Mead optimization method. Python implementation example

The Nelder – Mead method is an optimization method (search for a minimum) of a function of several variables. A simple and at the same time effective method to optimize functions without using gradients. The method is reliable and, as a rule, shows good results, although there is no theory of convergence. It can be used in the optimize function from the scipy.optimize module of the popular python library, which is used for mathematical calculations.

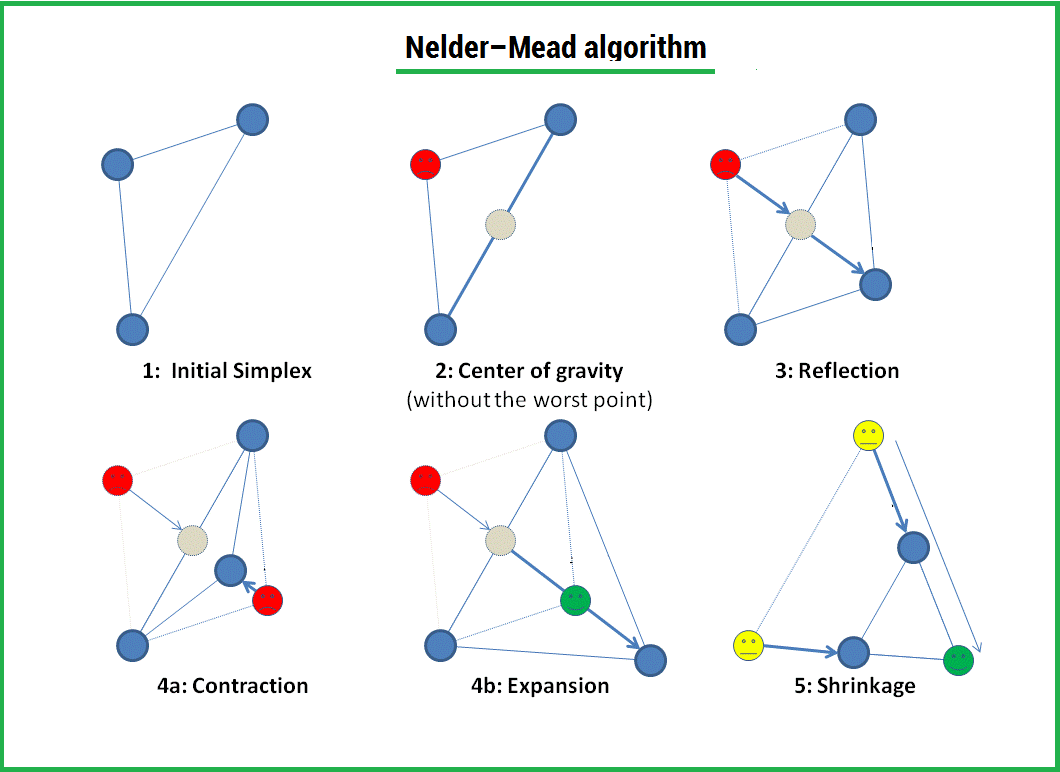
The algorithm consists in the formation of a simplex ( simplex ) and its subsequent deformation in the direction of the minimum, through three operations:

1) Reflection (reflection);
2) Stretching (expansion);
3) Compression (contract);
')
A simplex is a geometric figure, which is an n - dimensional generalization of a triangle. For one-dimensional space it is a segment, for two-dimensional it is a triangle. Thus, an n-dimensional simplex has n + 1 vertices.

Algorithm

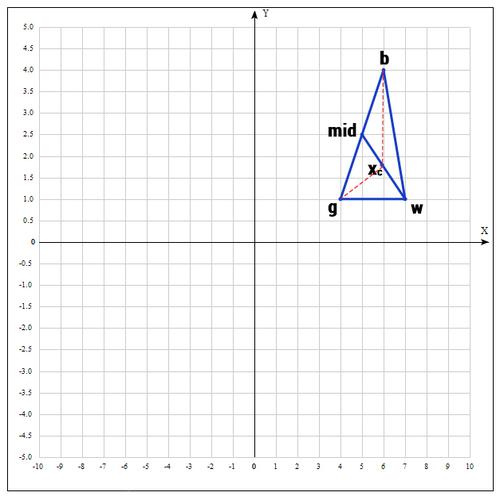
1) Let $$$f (x, y)$function that needs to be optimized. In the first step, we select three random points (more on this later) and form a simplex (triangle). We calculate the value of the function at each point: $$$f (V_1)$, $$$f (V_2)$, $$$f (V_3)$.

Sort points by function values $$$f (x, y)$at these points, we thus obtain a double inequality: $$$f (V_2) \ leq f (V_1) \ leq f (V_3).$

We are looking for the minimum of the function, and therefore, at this step, the best point will be at which the value of the function is minimal. For convenience, remap the points as follows:

b = $$$V_2$, g = $$$V_1$, w = $$$V_3$where best, good, worst - respectively.



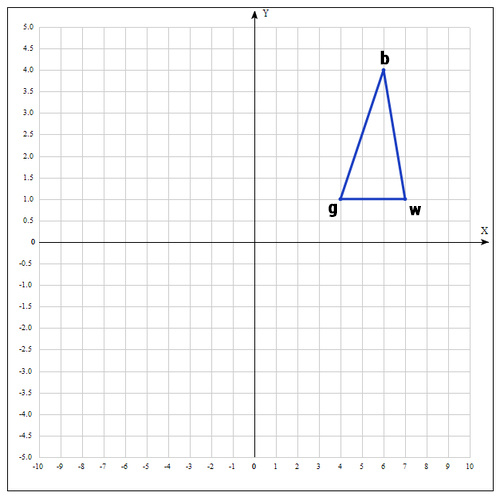
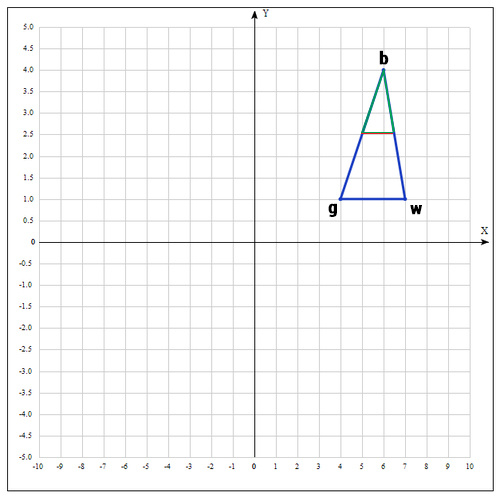
2) In the next step we find the middle of the segment, the points of which are g and b. Since the coordinates of the midpoint of the segment are equal to the half-sum of the coordinates of its ends, we get:

$$

$$mid = \ left (\ frac {x_1 + x_2} 2; \ frac {y_1 + y_2} 2 \ right)$$

In a more general form, you can write this:

$$

$$mid = \ frac 1 n \ sum_ {i = 1} ^ n x_i$$

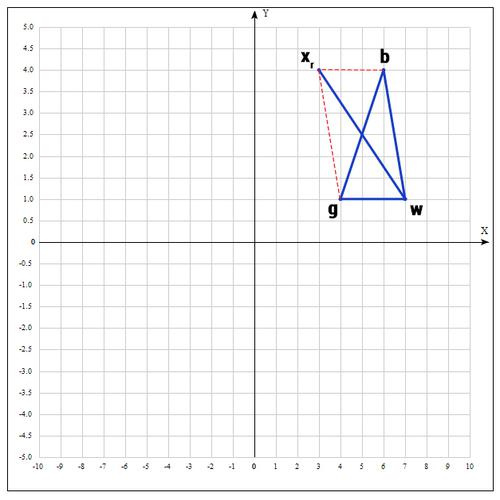
3) Apply the reflection operation:
Find the point $$$x_r$, in the following way:

$$

$$x_r = mid + α (mid - w)$$

Those. we actually reflect the point w relative to mid. As a coefficient, they are taken as a rule 1. We check our point: if $$$f (x_r) <f (g)$then this is a good point. And now we will try to increase the distance by 2 times, all of a sudden we will be lucky and we will find the point even better.



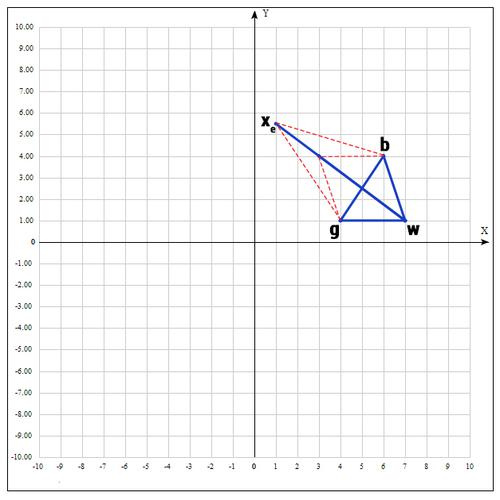
4) Apply the stretching operation:
Find the point $$$x_e$in the following way:

$$

$$x_e = mid + γ (x_r - mid)$$

As γ we take γ = 2, i.e. the distance is increased by 2 times.

Check point $$$x_e$:

If a $$$f (x_e) <f (b)$then we were lucky and we found the point better than it is at the moment, if this had not happened, we would have stopped at the point $$$x_r$.

Next, replace the point w with $$$x_e$in the end we get:



5) If we are completely unlucky and we have not found any good points, try the compression operation.
As follows from the name of the operation, we will reduce our segment and look for good points inside the triangle.

Trying to find a good point. $$$x_c$:

$$

$$x_c = mid + β (w - mid)$$

The coefficient β is taken equal to 0.5, i.e. point $$$x_c$in the middle of the segment wmid.



There is another operation - shrink (reduction). In this case, we redefine the whole simplex. We leave only the "best" point, the rest is defined as follows:

$$

$$x_j = b + δ (x_j - b)$$

The coefficient δ is taken equal to 0.5.

In essence, we move points towards the current “best” point. The conversion is as follows:



It should be noted that this operation is expensive, since it is necessary to replace points in the simplex. Fortunately, it has been established, when conducting a large number of experiments, that shrink transformation rarely happens in practice.

The algorithm ends when:

1) The required number of iterations was performed.
2) The area of ​​the simplex reached a certain value.
3) The current best solution has reached the required accuracy.

As with most heuristic methods, there is no perfect way to select initialization points. As already mentioned, you can take random points that are close to each other to form a simplex; but there is a better solution, which is used in the implementation of the algorithm in MATHLAB:

Select the first point $$$V_1$we charge the user if he has some idea of ​​a possible good solution, otherwise he is chosen randomly. The remaining points are selected based on $$$V_1$, a short distance along the direction of each dimension:

$$

$$V_ {i + 1} = V_i + h (V_1, i) * U_i$$

Where $$$U_i$- unit vector.
$$$h (V_1, i)$is defined as follows:
$$$h (V_1, i)$= 0.05, if the coefficient at $$$U_i$in the definition $$$V_1$not null.
$$$h (V_1, i)$= 0.00025, if the coefficient at $$$U_i$in the definition of zero.

Example:

Find the extremum of the following function: $$$f (x, y) = x ^ 2 + xy + y ^ 2 - 6x - 9y$

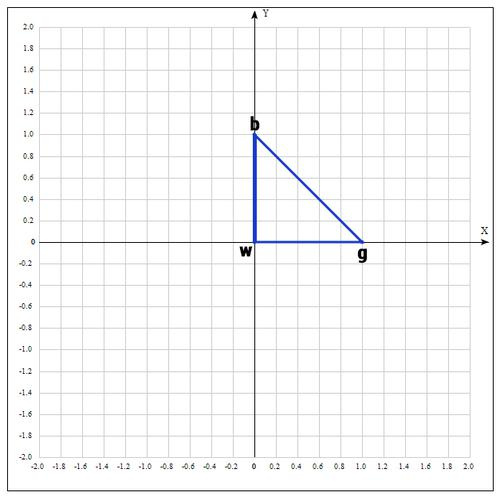
Let's take points as initial:

$$

$$V_1 (0, 0), V_2 (1, 0), V_3 (0, 1)$$

Calculate the value of the function at each point:

$$

$$f (V_1) = f (0, 0) = 0$$

$$

$$f (V_2) = f (1, 0) = -5$$

$$

$$f (V_3) = f (0, 1) = -8$$

Re-designate the points as follows:

$$

$$b = V_3 (0, 1), g = V_2 (1, 0), w = V_1 (0, 0)$$

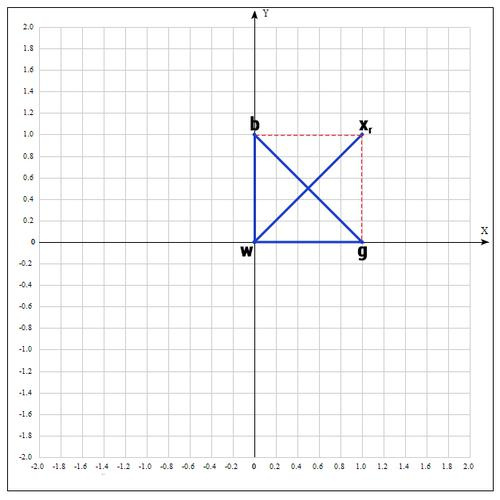
Find the middle of the segment bg:

$$

$$mid = \ frac {b + g} 2 = \ left (\ frac 1 2; \ frac 1 2 \ right)$$

Find the point $$$x_r$(reflection operation):

$$

$$x_r = mid + α (mid - w),$$

if α = 1, then:

$$

$$x_r = 2 * mid - w = 2 \ left (\ frac 1 2; \ frac 1 2 \ right) - \ left (0, 0 \ right) = (1, 1)$$

Check point $$$x_r$:

$$$f (x_r) = -12$because $$$f (x_r) <f (b)$try to increase the segment (stretching operation).

$$

$$x_e = mid + γ (x_r - mid),$$

if γ = 2, then:

$$

$$x_e = 2x_r - mid$$

$$

$$x_e = 2 (1, 1) - \ left (\ frac 1 2, \ frac 1 2 \ right) = (1.5, 1.5)$$

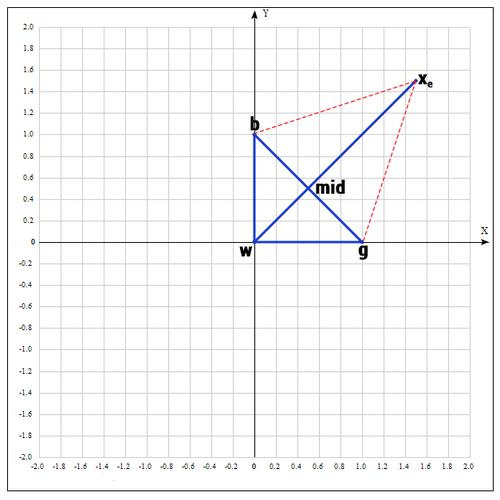
Check the value of the function at the point $$$x_e$:

$$

$$f (x_e) = f (1.5, 1.5) = -15.75$$

It turned out that the point $$$x_e$“Better” points b. Therefore, we get new vertices:

$$

$$V_1 (1.5, 1.5), V_2 (1, 0), V_3 (0, 1)$$

And the algorithm starts over.

Table of values ​​for 10 iterations:

Best	Good	Worst
$$$f (0, 1) = -8$	$$$f (1.0, 0) = -5$	$$$f (0, 0) = 0$
$$$f (1.5, 1.5) = -15.75$	$$$f (0, 1) = -8$	$$$f (1.0, 0) = -5$
$$$f (0.25, 3.75) = -20.187$	$$$f (1.5, 1.5) = -15.75$	$$$f (0, 1) = -8$
$$$f (0.25, 3.75) = -20.187$	$$$f (1.75, 4.25) = -20.1875$	$$$f (1.5, 1.5) = -15.75$
$$$f (1.125, 3.375) = -20.671$	$$$f (1.75, 4.25) = -20.1875$	$$$f (0.25, 3.75) = -20.1875$
$$$f (1.140, 3.796) = -20.9638$	$$$f (1.125, 3.375) = -20.6718$	$$$f (1.75, 4.25) = -20.1875$
$$$f (1.140, 3.796) = -20.9638$	$$$f (1.287, 3.751) = -20.8668$	$$$f (1.125, 3.375) = -20.6718$
$$$f (1.140, 3.796) = -20.9638$	$$$f (1.236, 3.874) = -20.9521$	$$$f (1.287, 3.751) = -20.8668$
$$$f (0.990, 4.002) = -20.9951$	$$$f (1.140, 3.796) = -20.9638$	$$$f (1.2365, 3.874) = -20.9520$
$$$f (0.990, 4.002) = -20.9951$	$$$f (0.895, 3.925) = -20.9855$	$$$f (1.140, 3.796) = -20.9638$

Analytically we find the extremum of the function, it is reached at the point $$$f (1, 4) = -21$.
After 10 iterations, we get a fairly accurate approximation: $$$f (0.990, 4.002) = -20.999916$

More about the method:

The Nelder – Mead algorithm is mainly used to select a parameter in machine learning. In essence, the simplex method is used to optimize model parameters. This is due to the fact that this method optimizes the objective function rather quickly and efficiently (especially where the shrink modification is not used).

On the other hand, due to the absence of the theory of convergence, in practice the method can lead to an incorrect answer even on smooth (continuously differentiable) functions. It is also possible that the working simplex is far from the optimal point, and the algorithm performs a large number of iterations, while slightly changing the values ​​of the function. The heuristic method for solving this problem is to run the algorithm several times and limit the number of iterations.

Implementation in the python programming language:

We create an auxiliary class Vector and overload operators to be able to perform basic operations with vectors. I intend not to use auxiliary libraries to implement the algorithm, since in this case, perception is often reduced.

#!/usr/bin/python # -*- coding: utf-8 -*- class Vector(object): def __init__(self, x, y): """ Create a vector, example: v = Vector(1,2) """ self.x = x self.y = y def __repr__(self): return "({0}, {1})".format(self.x, self.y) def __add__(self, other): x = self.x + other.x y = self.y + other.y return Vector(x, y) def __sub__(self, other): x = self.x - other.x y = self.y - other.y return Vector(x, y) def __rmul__(self, other): x = self.x * other y = self.y * other return Vector(x, y) def __truediv__(self, other): x = self.x / other y = self.y / other return Vector(x, y) def c(self): return (self.x, self.y) # objective function def f(point): x, y = point return x**2 + x*y + y**2 - 6*x - 9*y def nelder_mead(alpha=1, beta=0.5, gamma=2, maxiter=10): # initialization v1 = Vector(0, 0) v2 = Vector(1.0, 0) v3 = Vector(0, 1) for i in range(maxiter): adict = {v1:f(v1.c()), v2:f(v2.c()), v3:f(v3.c())} points = sorted(adict.items(), key=lambda x: x[1]) b = points[0][0] g = points[1][0] w = points[2][0] mid = (g + b)/2 # reflection xr = mid + alpha * (mid - w) if f(xr.c()) < f(gc()): w = xr else: if f(xr.c()) < f(wc()): w = xr c = (w + mid)/2 if f(cc()) < f(wc()): w = c if f(xr.c()) < f(bc()): # expansion xe = mid + gamma * (xr - mid) if f(xe.c()) < f(xr.c()): w = xe else: w = xr if f(xr.c()) > f(gc()): # contraction xc = mid + beta * (w - mid) if f(xc.c()) < f(wc()): w = xc # update points v1 = w v2 = g v3 = b return b print("Result of Nelder-Mead algorithm: ") xk = nelder_mead() print("Best poits is: %s"%(xk)) 

Thanks for reading the article. I hope she was useful to you and you have learned a lot.
With you was FUNNYDMAN. Successful optimization!)