Third Coming GOST 28147-89 or Russian Roulette

Until the mid-60s of the last century, in the era of arithmometers and slide rules, cryptographic systems were developed by engineers. Then the role of mathematicians was reduced to cryptanalysis and the introduction of hidden backdoors into algorithms.

With the advent of computers, mathematicians fully occupied the topic of cryptography, a digital representation of their patrimony data.

But progress does not stand still, quantum calculators and quantum data transfer appeared, and there the data are not represented as numbers, but as quantum states, this means the arrival of physicists in the topic of information processing.
')
While real quantum computations are in the region of the “transcendental distance”, but this does not mean that they are preparing for them early, it is quite possible that it is already too late. But better late than never.

In the meantime, mathematicians are poorly versed in the intricacies of programming, they invent something, and then the programmer must implement it in program code, which is not always possible to do effectively.

An example of this approach is the Grasshopper symmetric encryption algorithm; it is impossible to implement it effectively in the x86-64 software codes.

Let's do the opposite and see what happens ...

The programmer, who knows how the processor works, will develop the algorithm most effectively implemented on modern processors, and the physicist will tell you how to make it resistant to quantum cryptanalysis methods.

Cryptographers, as in the good old days, let them do their main work - the cryptanalysis of the resulting solution.

We will act cautiously, according to the principle of "The best is the enemy of the good," we take as a basis the "good" - GOST 28147-89. Then, following the medical principle “Do no harm”, we will strengthen it with the methods of multi-threaded calculations.

What it means to "strengthen" was stated in the article "Multi-threaded cryptographic algorithms ," which was specifically done:

- Increased the key size to 256 bytes.
- Increased data block size to 256 bytes.
- Improved statistical parameters of ciphertext.

Increasing the size of the key and data block is reduced to an increase in the calculated and algorithmic complexity of cryptanalysis. The requirement of maximum compliance of the ciphertext with the random sequence parameters was previously secondary, but at present it is already unacceptable.

Statistical characteristics of ciphertext in the post-quantum era become the main parameters determining cryptographic resistance.

Any violations of chance are hidden patterns that cryptographers can reduce to linear functions. And linear functions of any complexity are opened by quantum methods. Therefore, the statistics were focused on the development of a multi-threaded encryption algorithm based on GOST 28147-89.

The following has been done:

- The nonlinear tetrad substitution operation is replaced by a nonlinear permutation byte operation in the data block. A total of 16 fixed permutations are used.
- A nonlinear operation of inverting groups of bits is introduced in the linear cyclic shift transform.
- The Feistel network is modified into a ring network of its own production with preservation of the basic transformations GOST 28147-89. This is done to eliminate the reversibility of the transformation.
- Entering keys is made in the form of a reversible cryptographic transformation of permutation of bits.

Converting a bit permutation splits a 256-byte block into pieces of arbitrary length (according to the key information) and swaps them also depending on the key information. The keys in this transformation do not affect the contents of the data block (they do not change the number of zeros and units), they only mix the data block with an “external” influence.

How to analyze this conversion is not clear. There is no mathematical apparatus for analyzing arbitrary permutations in binary blocks performed on arbitrary fragments of this block ...

The modified Feistel network operates in the mode of irreversible gamming. This ensures that even knowing the keys and a certain sequence of gamma blocks it is impossible to calculate the values ​​of gamma blocks outside of this known sequence of blocks.
To calculate gamma block values ​​outside of a known sequence, it is required to perform a calculation from the starting point of gamming.

Practical implementation

While all this was a "fairy tale" and good wishes, it is time to turn them into a "true story", and this is how it looks:


This is a typical result of NIST tests of new crypto-transformation based on GOST 28147-89. The results of tests on any random keys and initial fillings always fit into the statistical parameters of a random sequence.

To reduce testing time, a simplified method was used. First, an experiment was conducted on a hundred blocks one million bits long in a gamut of 24 megabytes long (the first half of the gamut is used).

In the case of an unsuccessful experiment (falling out of the range of permissible proportions), the same gamma, already in full, was tested on blocks of two million bits in length. For such experiments, all test launches were successful (in a series of 100 experiments).

It is clear that tests with a block of two million bits in length should also sometimes lead to falling out of the range of proportions, but due to limitations on the number of experiments, there were no such cases.

These statistical parameters of the gamut are much better than the gamma produced by classical GOST, it often contains keys that the NIST tests do not pass in principle. The AES cipher in similar experiments is not much different from the traditional GOST.

The statistical parameters obtained in experiments on the norms of the 8-byte block cipher for a block cipher with a block size of 256 bytes are fantastic.

This is the same as, for example, throwing a coin 12 times and receiving an equal loss of "eagle" and "nutlets", to demand that the cube, also thrown 12 times, fall on each face twice a time ...

This is theoretically possible only with very high differential entropy between adjacent blocks and characterizes the level of complexity of the block cipher.

And the most interesting, these parameters are obtained with one round of conversion. There are no other block ciphers satisfying the requirements of randomness when using just one round.

The maximum cryptographic power of this cipher is already achieved in 16 rounds, but for the current level of cryptanalysis it is clearly redundant.

Now about the speed



This is a screenshot of the implementation of multi-threaded crypto-transformation based on GOST 28147-89 in the FastSecurityBoxes program, the testing was carried out according to the procedure described in the article “The Second Coming of GOST”.

As can be seen in the screenshot, the copy speed has reached the limit for test SSDs and is 453 MBytes / sec. when the processor is only 6 percent.

Theoretically, in tests of pure cryptography, the encryption speed for the gamming mode is 12 GBytes / sec. for one physical core of the processor (Skylake models and above) operating at a frequency of 3 GHz and above.

The encryption speed is no longer determined by the frequency of the processor, but by the bandwidth of the RAM of the computing system.

Russian Roulette, 2017 and its future application

Recently, with the help of the FSB, we began to receive ciphers with sonorous names, such as “Magma”, “Grasshopper”, and we will continue this tradition.

We will call this block cipher "Russian Roulette" .

Why "Russian", I hope everyone understands. A "roulette", because the cipher is built on the rotations (ring shifts) of binary sequences. Such shifts there are only explicitly 192 pieces per round.

By the way, the Russian officers who played Russian Roulette were crazy, but far from foolish. They thoroughly cleaned their revolvers, and knew physics well, and therefore kept the revolver while rotating the drum horizontally ...

A drum with one / five of the six bullets becomes unbalanced, and always strive to stand up empty chamber in front of the barrel.

So it was just an accident that the drum was jamming from different specks / hairs, getting to the empty chamber was “pseudo-random” and had a strict, predictable result.

Previously, when introducing a parallel implementation method to GOST 28147-89, I had to fully describe it, since it was officially certified by the FSB.

Now the situation is different, no official status is expected. Therefore, there will be no detailed description of the “Russian Roulette” algorithm, this is a kind of copyright protection. If it becomes interesting to become professionals, let them turn to their colleagues, - reverse programmers. That's who will have to break his head ...

In short, the Russian Roulette algorithm will be proprietary and this is coming soon: Russian Roulette, 2017 .

The encryption algorithm, closed from research, is of course nonsense, since there is no confidence in the encryption reliability.

But Russian Roulette is not an encryption system, we do not need a float with a regulator. Let me be the first to throw a stone at someone who says that this is a cipher, this is not an encryption system, the knight's move is made with a slight movement of the hand, and the algorithm is turned into a high-speed system of hashing and error correction, because first of all you need to take care of data integrity ...

The self-made Feistel cyclic network ideally meets the requirements of the “turbo code” for correcting errors, I did not do it on purpose, “he came” ...

Standard feedback gamma is converted to a hash function, if the keys are associated with previously processed data ...

Well, the fact that as a result, the data will also be reliably protected from viewing and modification - so sorry, a side effect of the system of hashing and error correction.

While the cryptographic “engine” of this future system is presented, it can be evaluated on test scales in terms of statistics and cryptographic resistance.

In the future, what Krylov failed to do was to be done. With the help of Russian roulette, we will bind the three members of his fable into the “cart” of responsible archiving, the “swan” of privacy, the “cancer” of authenticity and the “pike” of reliability. In this case, make them pull the "cart" at a breakneck pace ...

Difficult task, but solvable.

Practical implementation of crypto functions

The Russian Roulette algorithm is built into the demo version of the FastSecurityBoxes program in a partially cropped form. So far, for testing, only the basic transform operating in the gamming mode has been implemented. One round is used, this is enough for reliable passing of the NIST tests and cryptographic strength at the level of 2256 * 8 (the brute force direct attack option).

Keys are recalculated after issuing 64 kilobytes of gamma.

The algorithm itself is implemented on AVX commands using YMM registers, so this algorithm can effectively work only on the latest Intel processors (Skylake and higher).
On AMD processors, even the newest ones, the Russian Roulette algorithm will work slowly, since operations using YMM registers are implemented in them by firmware and not by hardware.

So that in the future, the FastSecurityBoxes program was required for practical work, it has a “payload” as a function of creating backup copies of logical disks (of course, recovery of disks is also there).

The choice of the applied task is determined on the one hand by the relevance of the topic, and on the other hand by the clarity of the result. Creating backup copies of the disks was naturally “sharpened” for high-speed SSD drives, which already today on the NVMe interface can work at a speed of 2-3 Gigabytes per second. At such speeds, nobody has yet been able to encrypt data, but now this is already a reality.

In addition to the new, yet exotic multi-threading algorithm, FastSecurityBoxes implements encryption according to the classical GOST 28147-89 in 8 parallel threads (for old processors) and 16 parallel threads (for skyleyka and above). These parallel encryption methods are certified by the FSB.

Encryption in 8 and 16 streams is included in the program for a substantive comparison of the results so that the difference could be felt ...

Apparently I confused readers with the terms "multi-threaded" and "parallel", so I will explain.
The parallel implementation method GOST 28147-89 is a certified FSB method. Parallelism involves the implementation of standard cryptographic procedures simultaneously on 4-8-16 independent physical devices. In this case, encryption keys, replacement blocks are the same everywhere, but the input and output data are different. Acceleration of work is achieved due to the simultaneous operation of several independent physical devices.

The term “independent physical device” as applied to a processor is a conventional concept, in reality, the processor has a set of registers on which the same transformations are performed simultaneously (with one processor command). But for simplicity of understanding, we will consider them independent physical devices operating strictly parallel and synchronous.

The multithreaded method implemented in the “Russian Roulette” algorithm differs significantly from the parallel one, here are its main differences:

1. There is a single block round converter.
2. The block length (so far) is 256 bytes and can be scaled.
3. Block fragments (two bytes each) are processed in independent streams.
4. Combining fragments produced in an additional transformation.

The multithreaded method allows you to increase the size of key data and the size of the input data block. Moreover, a change in any of the 2048 bits of the input block leads to a guaranteed change in all 2048 output bits after ten rounds of conversion.

Now the cipher contains 128 threads, when the processor with the AVX-512 command set appears, it will be possible to increase the number of threads to 512 (the data block will be 1 KB in size) and increase the speed twice.

In the meantime, the bottom line ..

The speed is 12 Gbytes per second for a processor with a frequency of 3 GHz, there is nothing to compare. The speed of the implementation of the algorithm “Russian Roulette” in the gamming mode “incomparable”. It is the fastest known pseudo-random sequence generator that meets the requirements of NIST tests.

The mathematical complexity of the cryptanalysis of the basic transformation “Russian Roulette” is determined by the dimension of the key, in our case it is equal to 2256 * 8.

The algorithmic complexity of cryptanalysis taking into account the known hacking methods for the basic Russian Roulette transformation is at least not less than the parent transformation of GOST 28147-89.

I will not overload the article with information about this new algorithm, while let the interested parties check what was said in the test program.

Download FastSecurityBoxes program here .

For testing, it provides the function of issuing a "clean" gamma. In this mode, test pseudorandom files are created for transformations in accordance with GOST 28147-89 and Russian Roulette.

PS

The FastSecurityBoxes program (Forced Secretive Images if in Russian) will soon turn into a responsible archiving program suitable for mass use, and then, I hope, into a full-featured commercial product. Accordingly, it is interesting to compare it with the commercial market backup luminaries in terms of copy speed and processor load.

The speed parameters of FastSecurityBoxes have already been cited in the article “The Second Coming of GOST”, let's see as an example what Acronis can do in the same modes of operation, on the same hardware platform.

Here's how it creates a sector dump without encryption and compression:



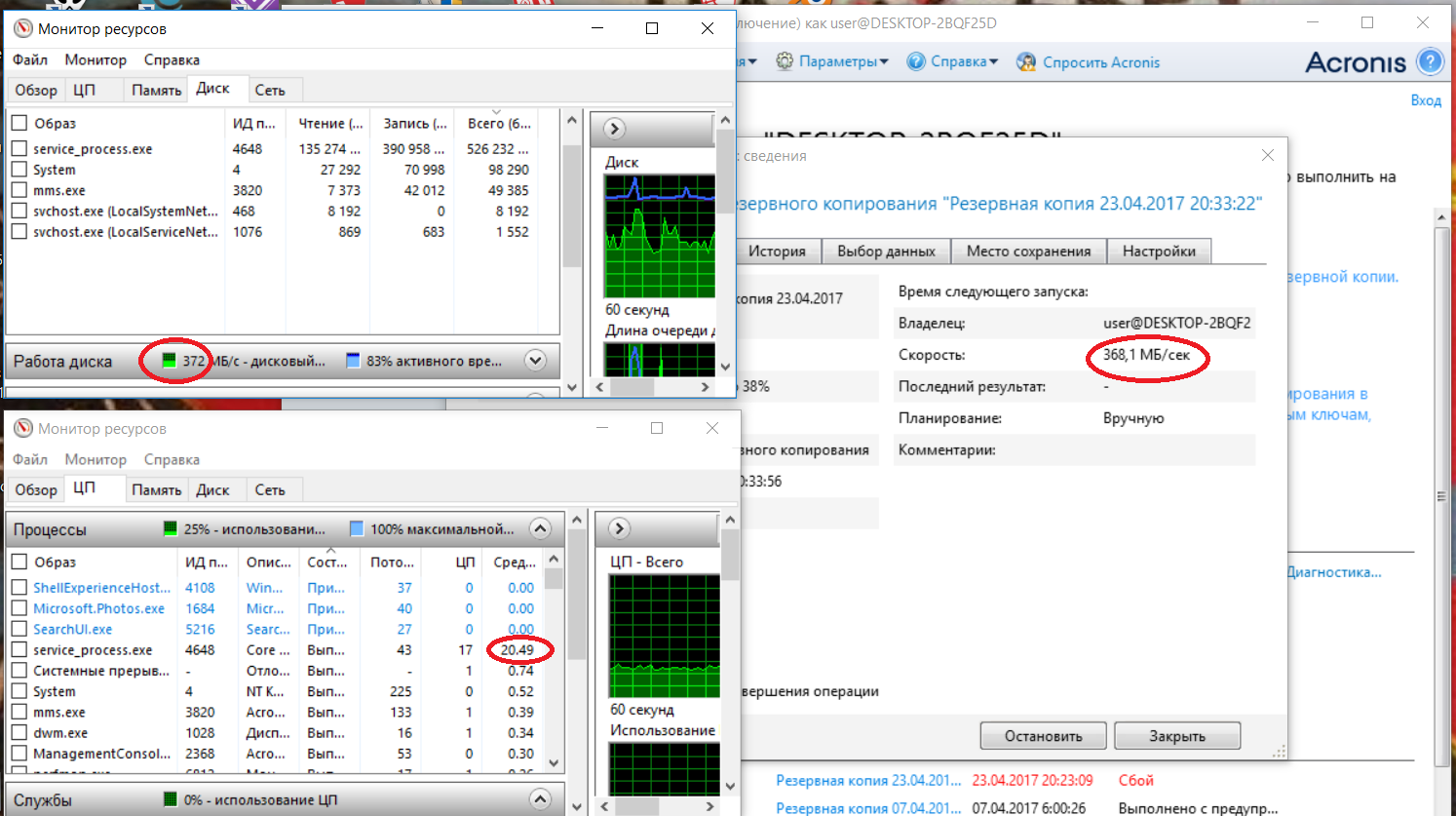
The program performs sector-by-sector copying at a speed of 368 MB / s ... Apparently, synchronous single-threaded I / O with cycles of waiting for the end of an I / O operation is used. Otherwise, do not explain too much CPU usage on I / O operations, which is 20%. Clearly outdated solution from the past millennium.

On the same hardware configuration, the FastSecurityBoxes test program provided a dumping speed of 450 MB / s. with a processor load of 6 percent.

Here is what Acronis issues on sector copying (without compression) with dump encryption according to GOST 28147-89:



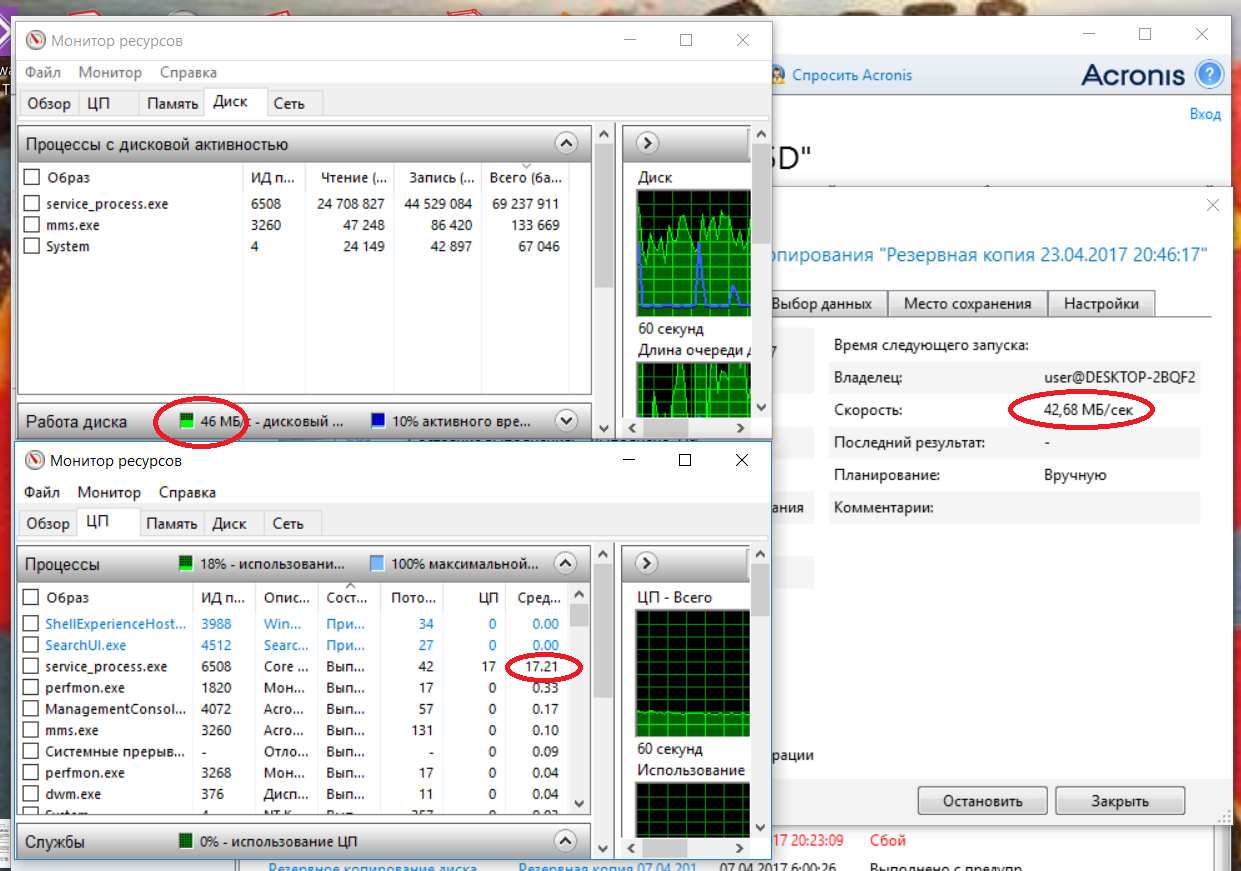
The speed dropped almost ten times, to 42 MB / s. using 17 percent of the processor's computing resources, FastSecurityBoxes provided 330 MB / sec in this mode, while using 10 percent of the computing resources, I think comments are superfluous ...

And the conclusion is obvious, Acronis uses an outdated classical implementation of GOST 28147-89 on the RON registers of the processor, therefore, such a low speed.

This is what Acronis does with encryption dump using the most “lightweight” AES-128 algorithm, again without compression. This algorithm for cryptographic resistance is worse than GOST 28147-89, but its implementation is the fastest due to the reduced number of rounds.



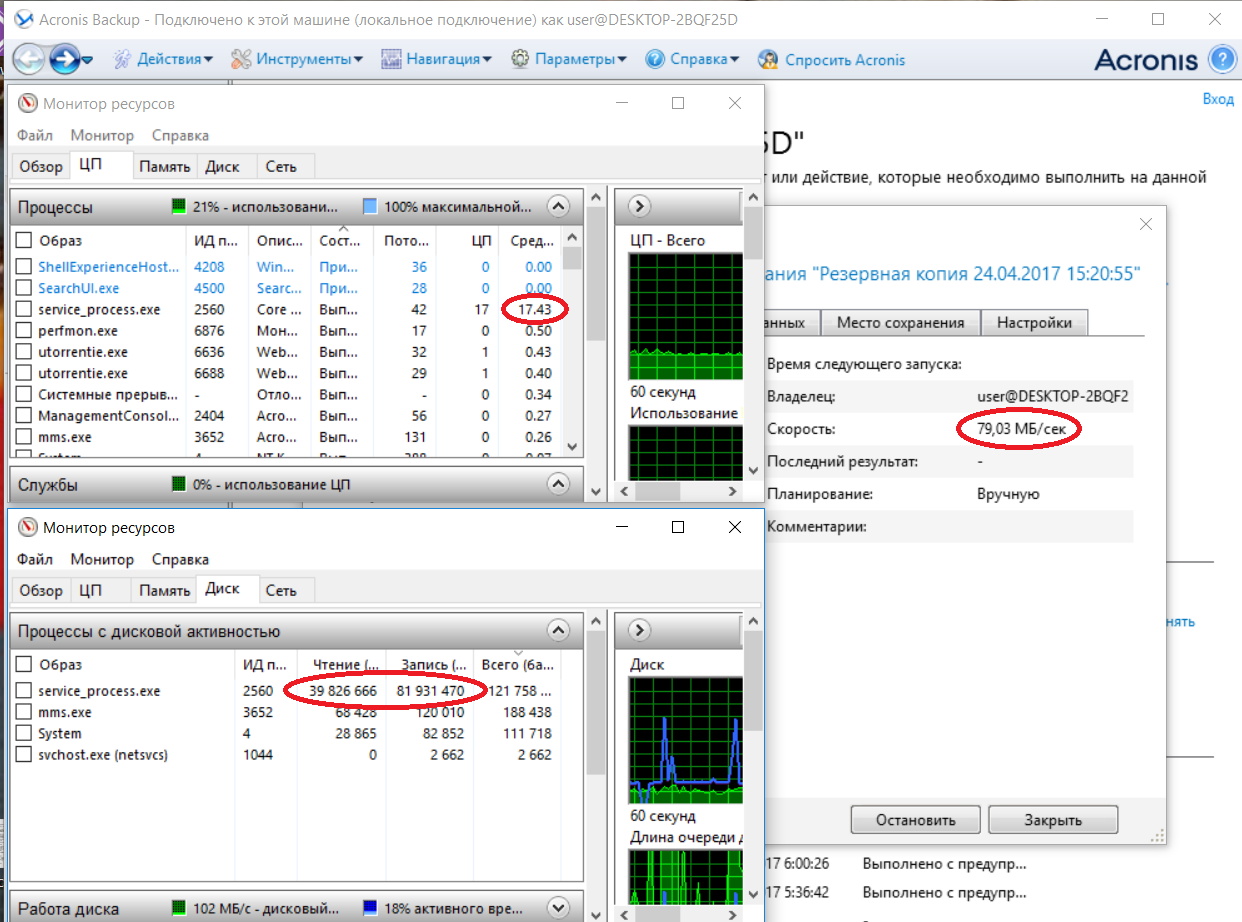
The speed has increased up to 80 MB / s, but still it is catastrophically low, BitLocker provided in this mode a speed of about 360 MB / s. Obviously, outdated crypto-library without the support of Intel hardware crypto accelerator is used.

How does all this look pale against the backdrop of modern technology ...