Algorithm for finding the best route in linux
Currently, IP is almost universally used in computer networks. In order to send an IP packet, each router searches its routing table for the best route for the destination address of the packet. In this article I want to describe the algorithm for finding the best route implemented in the linux kernel.
Usually they say that all routes are in the routing table, in which the search for the best route is performed. There may be terminological confusion. The fact is that under the routing table can be understood two different things, which are sometimes denoted by the terms Routing Information Base (RIB) and Forwarding Information Base (FIB). Both RIB and FIB do store ip routes, but the purpose of these structures and the algorithms for choosing the best routes in these structures are different.
Routing Information Base (RIB)
Routes to the router can come from various sources: be configured statically, come from dynamic routing protocols OSPF, BGP, etc. At the same time, routes with the same prefix can come from various sources. From these routes you need to choose one and add it to the FIB. This problem is just solved in the RIB. Usually, routes from different sources are assigned a different Administrative Distance and the route with the smallest Administrative Distance is considered the best. It is important that routes compete with one and the same prefix. Routes with different prefixes are not compared with each other. For example, the prefixes 10.0.0.0/8 and 10.0.0.0/16 are different prefixes and both routes will be included in the FIB. Thus, in the RIB, a SPECIFIC prefix is searched. The search for prefixes in the RIB is performed when adding or removing routes, which is relatively rare.
')
Forwarding Information Base (FIB)
The FIB itself serves to route ip-packets. Here the best route is the route with the longest prefix that matches the destination address in the ip-package. The joint work of RIB and FIB is shown in the figure:
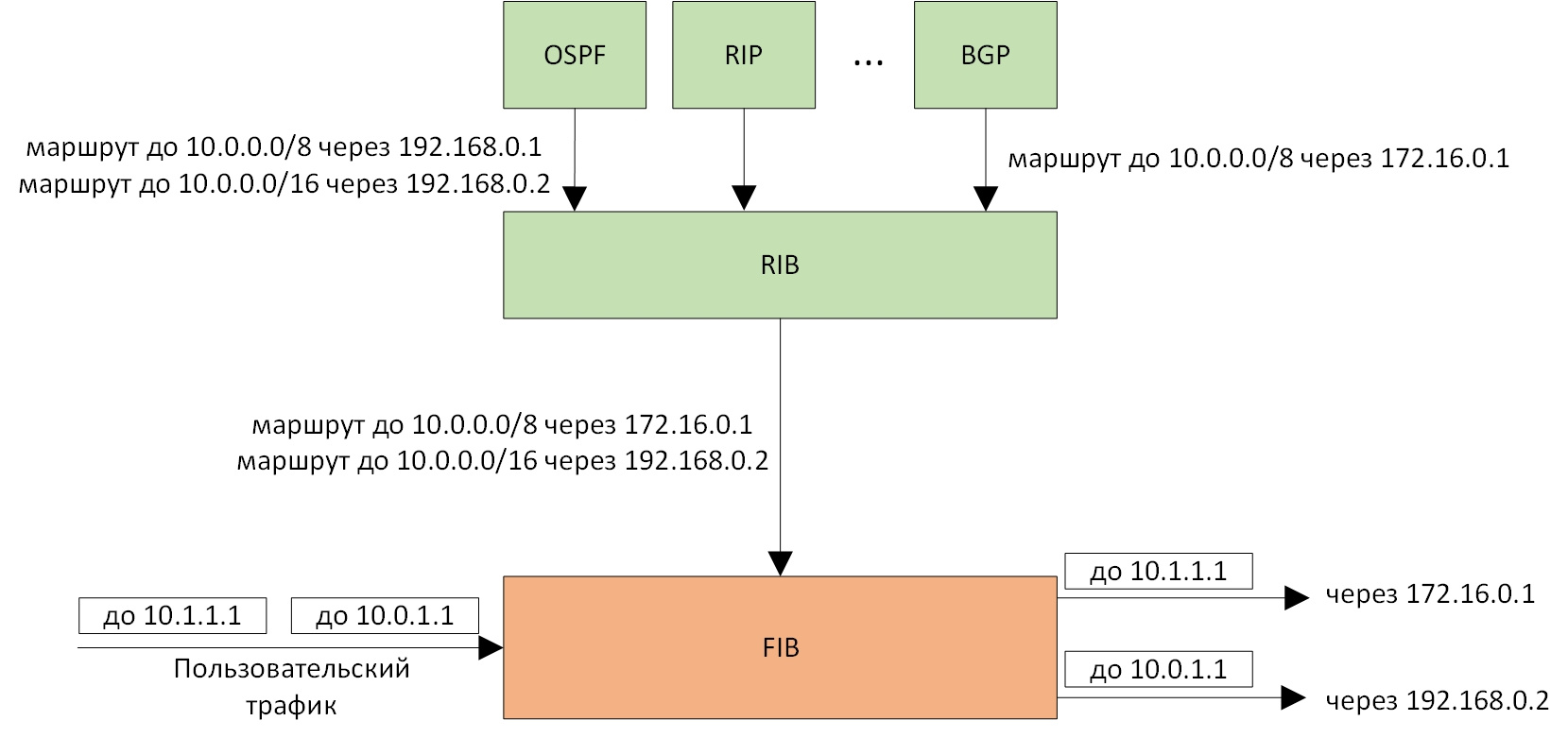
Figure 1. Collaboration between RIB and FIB. Routes from different routing protocols get into the RIB and are selected. The FIB performs packet routing according to the longest prefix.
Search for the best route in the FIB occurs for each new ip-package. The speed of the device routing directly depends on how effectively the route is searched for in the FIB. Therefore, the search in the FIB should be done as quickly and efficiently as possible. The FIB can contain several hundred thousand routes with different prefixes, so the task looks rather nontrivial. To optimize it, many different algorithms have been proposed. In this article I want to tell how the search in the FIB is implemented in the linux kernel.
Task statement
IP-prefix is usually denoted as ip-address and prefix length, for example: 10.0.0.0/8. It will be more convenient for us to represent the prefix in binary form, leaving only the left part equal to the prefix length and lowering its right nonessential part: 00001010. The default route (i.e., the zero length prefix will be denoted by an asterisk *. The search task looks like this. We have a set of different prefixes: *, 00, 10, 0000, 1000, 1001, 1010, 10111. We are given a destination address, which in binary form looks like this: 1010110001110100010001000010111. Among the available prefixes, you need to find the best one, ie The longest that matches the left side of the address n values. In our example, this will be the prefix 1010. Each prefix is associated with the ip-address of the next router (next-hop), outgoing interface, and other information sufficient to send the packet further.In the future, for simplicity, I will use the above set of prefixes and addresses destination length 6. All of the following also applies to real ip-addresses of length 32. You can see how the real list of prefixes in the FIB (in binary form) can look here .
We will consistently build the best prefix search algorithms starting from the simplest, gradually improving them until we come to the algorithm used in the linux kernel.
Trivial algorithm
The obvious and simplest algorithm is to simply search through all the available prefixes and select the best one. Such an algorithm is easy to implement, but on a large number of prefixes, the speed of its operation is completely unsatisfactory. If we have 500,000 prefixes in the FIB, then we need to go through and check them all.
Search speed can be slightly improved by storing prefixes in descending order of their length. Then the first matching prefix will be the longest and, therefore, the best.
Prefix tree
The natural way to organize prefixes is the prefix tree ( trie ). An example of a prefix tree for the prefixes *, 00, 10, 0000, 1000, 1001, 1010, 10111 is shown in the figure:
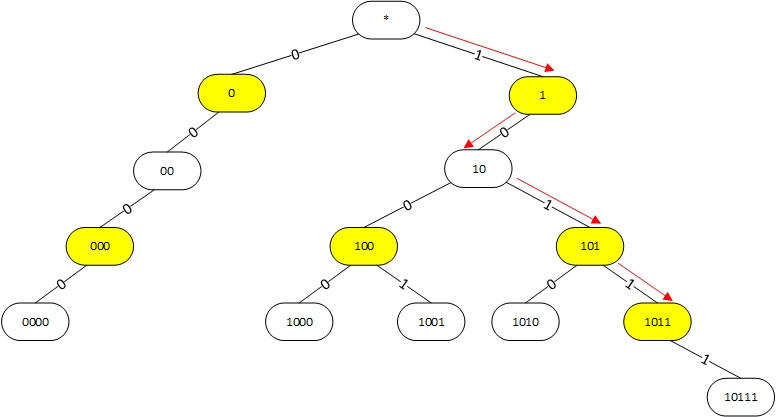
Figure 1. Using the prefix tree to find the longest prefix. The red arrows show the search sequence for address 101100.
White nodes correspond to the prefixes of interest. They also store a link to information about where to send the packet further (next-hop, etc.). Yellow nodes are intermediate and serve to properly organize the structure of the tree. The top node is the root of the tree and corresponds to the prefix 0.0.0.0/0. To find the best prefix, the leftmost bit of the destination address of the packet is checked. If it is 0, then we go down to the left, if it is 1, then to the right. Then we check the second bit, etc., gradually descending the tree while there is a possibility. Going down the tree, remember the last white node passed, it will be the best. For example, when searching for the best prefix for the address 101100, we successively go through the nodes *, 1, 10, 101, 1011. The last white prefix passed is 10, it will be the best.
The maximum number of comparisons, obviously, does not exceed the height of the tree and for ipv4 is equal to 32.
Compression path
If there are not very many prefixes, then chains can form in a prefix tree without branches. In such a chain, you can skip the yellow nodes with one child prefix, as shown in the figure. This mechanism is called Path compression and the tree thus constructed is Path compressed trie (PC-trie).
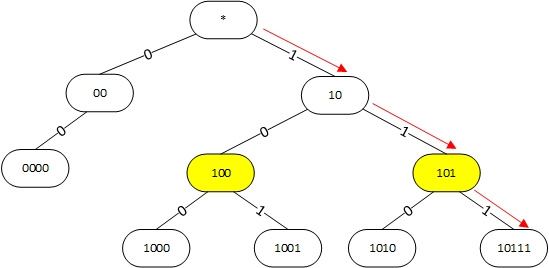
Figure 2. Using Path compressed trie to find the longest prefix for the address 101100.
The search algorithm remains virtually unchanged. To find the best prefix for the address 101100, we also first check the 1st bit of the address. Since it is equal to 1, we go down to the right in the prefix 10. Make sure that the prefix 10 fits. Next, check the 3rd bit of the address, go down to node 101, check the 4th bit, and get to node 10111. Prefix 10111 does not match the address and the last white prefix we visited, as in the previous case, is 10.
Level compression
Compressing the path effectively when the prefixes are relatively few. When the number of prefixes increases, another optimization becomes useful, called Level Compression. Here, for some nodes of the tree, we store not two children, but more, for example, 4, 8, 16, etc. As an index to select a child element, we use several bits at once in the address being checked. The tree using compression paths and levels is called Level and Path Compressed Trie (LPC-Trie).
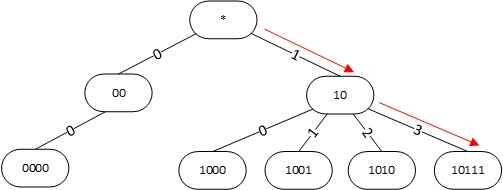
Figure 3. Using Level and Path compressed trie to find the longest prefix for the address 101100.
In this case, node 10 has not four child nodes, but four. To select a child node in the destination address, two bits are checked at once: the 3rd and 4th, and are used as an index to select a child node. So, at address 101100, these bits are 11 (decimal 3), i.e. after node 10 we descend to the child node with index 3, i.e. in node 10111. Since it does not fit, the longest prefix is 10.
The more bits of the destination address are used to find the next node, the smaller the tree height and the faster the search. However, for some indexes, the child nodes are missing and part of the memory is wasted.
Implementation in linux
For verification, I took the linux 4.4.60 kernel. The linux kernel uses the modified LPC-Trie to find the best prefix. When compressing a level, the maximum number of bits is used, at which the number of missing children does not exceed the number of existing children.
The modification is that all white prefixes are moved to the end nodes of the tree. Intermediate nodes are used exclusively for organizing the tree structure. In one final node there may be a chain of several prefixes that differ from each other in the number of zeros to the right, that is, for example: 1, 10, 1000, as shown in the figure:
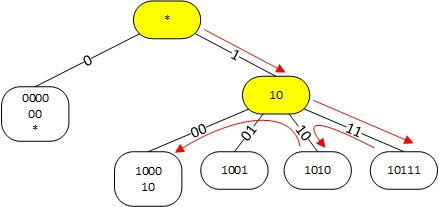
Figure 4. Linux trie implementation to find the longest prefix for the 101100 address.
The end node is searched using the LPC algorithm. Then all the prefixes in the destination node are sequentially searched, starting with the longest. The situation at the same time is complicated by the fact that in some cases the best route is missed when going down a tree and to find it you need to check the nodes on the left (backtracking). So, for the address 101100, we descend to node 10111. Since it does not contain the required prefix, we have to check node 1010 (the prefix 101 can be stored in it) and then node 1000 and find the prefix 10. It fortunately requires backtracking , apparently not very often and not greatly reduces the search speed.
For what purposes is this modification made, which complicates and slows down the search, it is not quite clear to me, perhaps it facilitates the construction of a tree when adding or removing routes, or it may simply be inherited from some algorithm.
In linux, you can view the FIB tree. To do this, enter the command cat / proc / net / fib_trie. This gives something similar to:
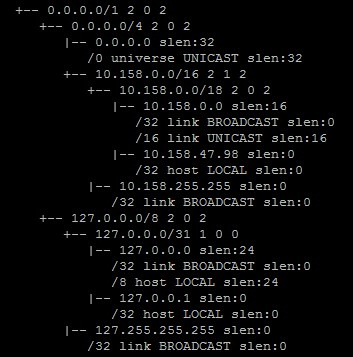
Figure 5. Output from the cat / proc / net / fib_trie command
Intermediate nodes of the tree are marked with + - symbols, end nodes with | - symbols. At the end nodes are visible prefixes, ordered by length.
DIR-24-8
Is it still possible to speed up the search for the best prefix? It turns out you can, if it sacrifices memory. If we assume that we have any amount of memory, then we can organize the search for the best prefix for a single memory access. To do this, you need to create a large array, in the cells of which you store references to the best prefixes, and use the destination address as the index when choosing a cell. For our example, the array will look like this:

Figure 6. Array to search for the longest prefix in one call.
To find the best prefix for the address 101100, we simply look at the cell with the index 101100 in binary form, i.e. with index 44, and immediately find that the best prefix is 10.
For such storage of prefixes, an array with the number of cells 2 to the extent of the destination address is needed, i.e. for addresses of length 6, 64 cells were needed, and for real ip-addresses of length 32, more than 4 billion cells would be needed.
To reduce the number of cells, we note that in our case, almost all prefixes are equal to 4 or less. Therefore, for almost all destinations, it suffices to look only at the first four bits. The streamlined search pattern looks like this:

Figure 7. Arrays for finding the longest prefix in a maximum of two hits.
In this case, two arrays are used. At first, the search is performed in the left array (out of 16 cells), using the first four bits of the destination address as the index. In all cases where the destination address does not start with 1011 (eleven in decimal), we immediately get the best prefix. Otherwise, we look at the last two bits of the address and use them as an index in the second table (from 4 cells). It can be seen that for the address 101100 we again get the best prefix 10. Thus, when searching for the best prefix, in most cases it is performed in one call, in the worst case in two.
In the case of real ip-addresses can be used a similar scheme. Most of the prefixes in FIB are length 24 or less. Therefore, it is logical to use an array indexed by the upper 24 bits of the address (16,777,216 cells) as the left array. For rare cases when the length of stored prefixes is longer than 24, additional tables are used, indexed by the last 8 bits of the prefix (256 cells for each additional table).
This fast search method (a maximum of two hits) is called DIR-24-8 and is used, for example, in DPDK .
Usually they say that all routes are in the routing table, in which the search for the best route is performed. There may be terminological confusion. The fact is that under the routing table can be understood two different things, which are sometimes denoted by the terms Routing Information Base (RIB) and Forwarding Information Base (FIB). Both RIB and FIB do store ip routes, but the purpose of these structures and the algorithms for choosing the best routes in these structures are different.
Routing Information Base (RIB)
Routes to the router can come from various sources: be configured statically, come from dynamic routing protocols OSPF, BGP, etc. At the same time, routes with the same prefix can come from various sources. From these routes you need to choose one and add it to the FIB. This problem is just solved in the RIB. Usually, routes from different sources are assigned a different Administrative Distance and the route with the smallest Administrative Distance is considered the best. It is important that routes compete with one and the same prefix. Routes with different prefixes are not compared with each other. For example, the prefixes 10.0.0.0/8 and 10.0.0.0/16 are different prefixes and both routes will be included in the FIB. Thus, in the RIB, a SPECIFIC prefix is searched. The search for prefixes in the RIB is performed when adding or removing routes, which is relatively rare.
')
Forwarding Information Base (FIB)
The FIB itself serves to route ip-packets. Here the best route is the route with the longest prefix that matches the destination address in the ip-package. The joint work of RIB and FIB is shown in the figure:

Figure 1. Collaboration between RIB and FIB. Routes from different routing protocols get into the RIB and are selected. The FIB performs packet routing according to the longest prefix.
Search for the best route in the FIB occurs for each new ip-package. The speed of the device routing directly depends on how effectively the route is searched for in the FIB. Therefore, the search in the FIB should be done as quickly and efficiently as possible. The FIB can contain several hundred thousand routes with different prefixes, so the task looks rather nontrivial. To optimize it, many different algorithms have been proposed. In this article I want to tell how the search in the FIB is implemented in the linux kernel.
Task statement
IP-prefix is usually denoted as ip-address and prefix length, for example: 10.0.0.0/8. It will be more convenient for us to represent the prefix in binary form, leaving only the left part equal to the prefix length and lowering its right nonessential part: 00001010. The default route (i.e., the zero length prefix will be denoted by an asterisk *. The search task looks like this. We have a set of different prefixes: *, 00, 10, 0000, 1000, 1001, 1010, 10111. We are given a destination address, which in binary form looks like this: 1010110001110100010001000010111. Among the available prefixes, you need to find the best one, ie The longest that matches the left side of the address n values. In our example, this will be the prefix 1010. Each prefix is associated with the ip-address of the next router (next-hop), outgoing interface, and other information sufficient to send the packet further.In the future, for simplicity, I will use the above set of prefixes and addresses destination length 6. All of the following also applies to real ip-addresses of length 32. You can see how the real list of prefixes in the FIB (in binary form) can look here .
We will consistently build the best prefix search algorithms starting from the simplest, gradually improving them until we come to the algorithm used in the linux kernel.
Trivial algorithm
The obvious and simplest algorithm is to simply search through all the available prefixes and select the best one. Such an algorithm is easy to implement, but on a large number of prefixes, the speed of its operation is completely unsatisfactory. If we have 500,000 prefixes in the FIB, then we need to go through and check them all.
Search speed can be slightly improved by storing prefixes in descending order of their length. Then the first matching prefix will be the longest and, therefore, the best.
Prefix tree
The natural way to organize prefixes is the prefix tree ( trie ). An example of a prefix tree for the prefixes *, 00, 10, 0000, 1000, 1001, 1010, 10111 is shown in the figure:

Figure 1. Using the prefix tree to find the longest prefix. The red arrows show the search sequence for address 101100.
White nodes correspond to the prefixes of interest. They also store a link to information about where to send the packet further (next-hop, etc.). Yellow nodes are intermediate and serve to properly organize the structure of the tree. The top node is the root of the tree and corresponds to the prefix 0.0.0.0/0. To find the best prefix, the leftmost bit of the destination address of the packet is checked. If it is 0, then we go down to the left, if it is 1, then to the right. Then we check the second bit, etc., gradually descending the tree while there is a possibility. Going down the tree, remember the last white node passed, it will be the best. For example, when searching for the best prefix for the address 101100, we successively go through the nodes *, 1, 10, 101, 1011. The last white prefix passed is 10, it will be the best.
The maximum number of comparisons, obviously, does not exceed the height of the tree and for ipv4 is equal to 32.
Compression path
If there are not very many prefixes, then chains can form in a prefix tree without branches. In such a chain, you can skip the yellow nodes with one child prefix, as shown in the figure. This mechanism is called Path compression and the tree thus constructed is Path compressed trie (PC-trie).

Figure 2. Using Path compressed trie to find the longest prefix for the address 101100.
The search algorithm remains virtually unchanged. To find the best prefix for the address 101100, we also first check the 1st bit of the address. Since it is equal to 1, we go down to the right in the prefix 10. Make sure that the prefix 10 fits. Next, check the 3rd bit of the address, go down to node 101, check the 4th bit, and get to node 10111. Prefix 10111 does not match the address and the last white prefix we visited, as in the previous case, is 10.
Level compression
Compressing the path effectively when the prefixes are relatively few. When the number of prefixes increases, another optimization becomes useful, called Level Compression. Here, for some nodes of the tree, we store not two children, but more, for example, 4, 8, 16, etc. As an index to select a child element, we use several bits at once in the address being checked. The tree using compression paths and levels is called Level and Path Compressed Trie (LPC-Trie).

Figure 3. Using Level and Path compressed trie to find the longest prefix for the address 101100.
In this case, node 10 has not four child nodes, but four. To select a child node in the destination address, two bits are checked at once: the 3rd and 4th, and are used as an index to select a child node. So, at address 101100, these bits are 11 (decimal 3), i.e. after node 10 we descend to the child node with index 3, i.e. in node 10111. Since it does not fit, the longest prefix is 10.
The more bits of the destination address are used to find the next node, the smaller the tree height and the faster the search. However, for some indexes, the child nodes are missing and part of the memory is wasted.
Implementation in linux
For verification, I took the linux 4.4.60 kernel. The linux kernel uses the modified LPC-Trie to find the best prefix. When compressing a level, the maximum number of bits is used, at which the number of missing children does not exceed the number of existing children.
The modification is that all white prefixes are moved to the end nodes of the tree. Intermediate nodes are used exclusively for organizing the tree structure. In one final node there may be a chain of several prefixes that differ from each other in the number of zeros to the right, that is, for example: 1, 10, 1000, as shown in the figure:

Figure 4. Linux trie implementation to find the longest prefix for the 101100 address.
The end node is searched using the LPC algorithm. Then all the prefixes in the destination node are sequentially searched, starting with the longest. The situation at the same time is complicated by the fact that in some cases the best route is missed when going down a tree and to find it you need to check the nodes on the left (backtracking). So, for the address 101100, we descend to node 10111. Since it does not contain the required prefix, we have to check node 1010 (the prefix 101 can be stored in it) and then node 1000 and find the prefix 10. It fortunately requires backtracking , apparently not very often and not greatly reduces the search speed.
For what purposes is this modification made, which complicates and slows down the search, it is not quite clear to me, perhaps it facilitates the construction of a tree when adding or removing routes, or it may simply be inherited from some algorithm.
In linux, you can view the FIB tree. To do this, enter the command cat / proc / net / fib_trie. This gives something similar to:

Figure 5. Output from the cat / proc / net / fib_trie command
Intermediate nodes of the tree are marked with + - symbols, end nodes with | - symbols. At the end nodes are visible prefixes, ordered by length.
DIR-24-8
Is it still possible to speed up the search for the best prefix? It turns out you can, if it sacrifices memory. If we assume that we have any amount of memory, then we can organize the search for the best prefix for a single memory access. To do this, you need to create a large array, in the cells of which you store references to the best prefixes, and use the destination address as the index when choosing a cell. For our example, the array will look like this:

Figure 6. Array to search for the longest prefix in one call.
To find the best prefix for the address 101100, we simply look at the cell with the index 101100 in binary form, i.e. with index 44, and immediately find that the best prefix is 10.
For such storage of prefixes, an array with the number of cells 2 to the extent of the destination address is needed, i.e. for addresses of length 6, 64 cells were needed, and for real ip-addresses of length 32, more than 4 billion cells would be needed.
To reduce the number of cells, we note that in our case, almost all prefixes are equal to 4 or less. Therefore, for almost all destinations, it suffices to look only at the first four bits. The streamlined search pattern looks like this:

Figure 7. Arrays for finding the longest prefix in a maximum of two hits.
In this case, two arrays are used. At first, the search is performed in the left array (out of 16 cells), using the first four bits of the destination address as the index. In all cases where the destination address does not start with 1011 (eleven in decimal), we immediately get the best prefix. Otherwise, we look at the last two bits of the address and use them as an index in the second table (from 4 cells). It can be seen that for the address 101100 we again get the best prefix 10. Thus, when searching for the best prefix, in most cases it is performed in one call, in the worst case in two.
In the case of real ip-addresses can be used a similar scheme. Most of the prefixes in FIB are length 24 or less. Therefore, it is logical to use an array indexed by the upper 24 bits of the address (16,777,216 cells) as the left array. For rare cases when the length of stored prefixes is longer than 24, additional tables are used, indexed by the last 8 bits of the prefix (256 cells for each additional table).
This fast search method (a maximum of two hits) is called DIR-24-8 and is used, for example, in DPDK .
Source: https://habr.com/ru/post/331944/
All Articles