Prüfer code
Trees Briefly recall
Tree - a special case of the graph. Trees are widely used in programming. A tree is a connected graph without cycles. A tree is called tagged if each vertex has a unique label. Usually this number.
Definition Building a Prüfer code for a given tree
The Prüfer code is a one-to-one coding method for labeled trees with n vertices using a sequence of n-2 integers in the interval [1, n]. That is, it can be said that the Prüfer code is a bijection between all spanning trees of the complete graph and numerical sequences.
This method of coding trees was proposed by the German mathematician Heinz Prüfer in 1918.
Consider the algorithm for constructing a Prüfer code for a given tree with n vertices.
At the entrance is a list of edges. The leaf of the tree with the smallest number is selected, then it is removed from the tree, and the number of the vertex that was associated with this leaf is added to the Prüfer code. This procedure is repeated n-2 times. In the end, only 2 vertices will remain in the tree, and the algorithm ends here. The numbers of the remaining two vertices are not recorded in the code.
Thus, the Prüfer code for a given tree is a sequence of n-2 numbers, where each number is the number of the vertex associated with the smallest leaf at that time — that is, the number in the segment [1, n].
Example
Source tree
Prüfer code: 1
Prüfer code: 1 5
Prüfer code: 1 5 2
Prüfer code: 1 5 2 6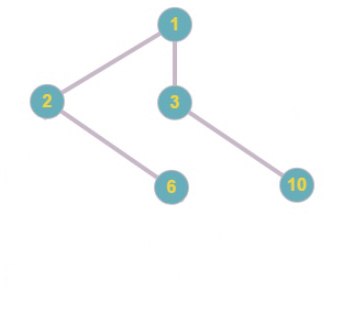
Prüfer code: 1 5 2 6 6
Prüfer code: 1 5 2 6 6 2
Prüfer code: 1 5 2 6 6 2 1
Prüfer code: 1 5 2 6 6 2 1 3
Restoration of a tree by its Prüfer code
Next to the task of constructing the Prüfer code is the task of recovering the encoded tree. We will consider an algorithm for restoring a tree with the following conditions: the input is a sequence of numbers (vertices) that represents the Prüfer code, the result will be a list of edges of the tree. Thus, the problem will be solved.
Consider the decoding algorithm in detail. In addition to the code, we need a list of all the vertices of the graph. We know that the Prüfer code consists of n-2 vertices, where n is the number of vertices in the graph. That is, we can determine the number of vertices in an encoded tree by the size of the code.
As a result, at the beginning of the algorithm, we have an array from the Prüfer code of size n-2 and an array of all vertices of the graph: [1 ... n]. Then the procedure is repeated n-2 times: the first element of the array containing the Prüfer code is taken, and the array with the tree vertices is searched for the smallest vertex not contained in the array with the code. The found vertex and the current element of the array with the Prüfer code constitute the edge of the tree. These vertices are removed from the corresponding arrays, and the procedure described above is repeated until there are no elements in the array with the code. At the end of the algorithm, two vertices will remain in the array with the vertices of the graph; they constitute the last edge of the tree. As a result, we obtain a list of all edges of the graph that has been encoded.
Example
Restore the tree using the Prüfer code, which was obtained in the encoding example.
First step
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 4
List of edges: 1 4
Second step
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 7
List of edges: 1 4, 5 7
Third step
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 5
List of edges: 1 4, 5 7, 2 5
Fourth step
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 8
List of edges: 1 4, 5 7, 2 5, 6 8
Fifth step
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 9
List of edges: 1 4, 5 7, 2 5, 6 8, 6 9
Sixth step
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 6
List of edges: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6
Seventh Step
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 2
List of edges: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2
Eighth step
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 1
List of edges: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1
Completion of the algorithm
Prüfer code: 1 5 2 6 6 2 1 3
Array of tree tops: 1 2 3 4 5 6 7 8 9 10
The minimum vertex not contained in the Prüfer code is 1
List of edges: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1, 3 10
Conclusion
The Prüfer code was proposed as a clear and simple proof of Cayley’s formula for the number of labeled trees. In practice, it is used more often to solve combinatorial problems.
Sources
- Wilson R. Introduction to graph theory. Translation from English M .: Mir, 1977. -208 p.
- Combinatorics. Boolean functions. Counts: studies. manual / A. A. Balagura, O. V. Kuzmin. - Irkutsk: Publishing house of ISU, 2012. - 115 p.
- MAXimal [Electronic Resource] - Access Mode: link , free. (the date of the appeal: 04.22.2017)
')
Source: https://habr.com/ru/post/331836/
All Articles