Postquantum reincarnation of the Diffie-Hellman algorithm: past and present

As you know, the last revolution in cryptography happened in 1976 due to the article “New Directions in Cryptography” by the American scientists Whitfield Diffie and Martin Hellman. This work turned out for the subsequent development of cryptography as the “Big Bang” - there was the birth of a new asymmetric cryptography universe. Up to this point (in any case, in the open press) there existed only symmetric cryptography. For the first time, young people and then unknown scientists proposed a scheme in which the subscribers initially did not need to share any secret keys to develop a shared secret. In addition to its primordial nature, this algorithm is interesting because, despite the fact that the “complex” tasks that underlie its security can become outdated, they can be successfully replaced by new ones. Initially, this was the discrete logarithm problem in the multiplicative group of a finite field (Discrete Logarithm Problem, abbr. - DLP), now in practice the discrete logarithm problem in the group of points of the elliptic curve (ECDLP) is widely used. In the future (not so distant) it is supposed to use other “complex” tasks, which will have exponential complexity not only on the classical, but also on the quantum computer. They are called postquantum. One of these tasks is the problem of finding isogeny between elliptic curves, which I want to talk about in this article.

Since the goal of the article is to explain as simply as possible the new mathematical “engine” for the Diffie-Hellman protocol (Diffie-Hellman or abbreviated DH), some attacks are not considered: we assume that the attacker can only read the messages in the channel, but cannot interfere in the work of the channel to intercept messages of subscribers and send their own (ie, the attacker is not “Man in the middle”). In practice (for example, in the TLS protocol), DH’s public keys can be signed and then Man can’t replace the DH key in the Middle: the DH public key comes from the server to the client as a certificate, from the client to the server is a temporary (ephemeral) key signed on a permanent client's private key. In general, in a harsh reality, the PKI technology, based on the trust of both parties to one CA, rescues DH from replacing public keys. But, again, in order not to distract the reader from the main thing - mathematics, I don’t write anything about PKI in this article. And once again: because there are cases when systems were implemented and implemented in which the parties exchanged temporary (ephemeral) public keys that the parties did not check (apparently those who designed them considered themselves too busy to learn the basics of cryptography or at least contact the experts), please do not forget that in real life it is necessary. The Man in the Middle (he is the Mediator, he is the Man-in-the-middle) is not the Snowman, and he exists.

Past: Classic Diffie-Hellman

Alice and Bob initially choose the parameters (domain parameters): the multiplicative group of the finite field and g - the generator of its subgroups. There is nothing wrong with the word generator. This is just one of the elements of the group with the following property: if we take its degrees from 1 to the number of elements of the group, we get the whole group. A subgroup is a subset of a group, which in itself is also a group (by multiplying its elements in any combination, we only get the elements of this very subset).

Example: $$$F_p ^ *$- multiplicative group of a finite field.

Elements of the group:

numbers from 1 to p - 1, where p is a prime number.

Group operation a * b mod p: multiply the elements of a and b, then divide a * b by p. The remainder of dividing a * b by p is the result of the operation a * b mod p.

For example, let the p module be 11. Most commonly referred to as $$$F_ {11} ^ *$. It consists of 11 - 1 = 10 elements: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

The number of elements in a group is called a group order. Order $$$F_ {11} ^ *$equals 10.

And now let's play a little with operations:

5 * 6 mod 11 = 8,

1 * 10 mod 11 = 10.

')

1 for this group is a neutral element. Neutral - because it “does not interact” with any other elements and the result of the operation with it is always equal to the second element of the operation. In this case, 1 * 10 mod 11 is 10.

6 * 2 mod 11 = 1.

For any element of any group there is an inverse element that “turns” it into a neutral one. For this group, 6 and 2 are opposite for each other.

When a group operation is called multiplication (as in the case of $$$F_p ^ *$), then use such designations to inverse to $$$a$item: $$$a ^ {- 1}$Those. $$$a$* $$$a ^ {- 1} *$= 1 What else can you say about this group? It is commutative (or abelian):

$$$a * b$mod p = $$$b * a$mod p: from the permutation a and b, the result does not change.

The generators of a group are those of its elements, all degrees of which are all elements of the group. Groups in which there is at least one such element are called cyclic. How to understand that x is a generator? The most primitive method: build a table of degrees x:

What about degrees 2?

2 * 2 mod 11 = 4

4 * 2 mod 11 = 8

8 * 2 mod 11 = 5

5 * 2 mod 11 = 10

10 * 2 mod 11 = 9

9 * 2 mod 11 = 7

7 * 2 mod 11 = 3

3 * 2 mod 11 = 6

6 * 2 mod 11 = 1 - we see that the cycle is closed. Degrees 2 generate the whole group. $$$F_ {11} ^ *$.

Total: 2 - generator $$$F_ {11} ^ *$.

The element order is the minimum degree to which it must be raised in order to get neutral. Order 2 in $$$F_ {11} ^ *$equals 10.

Now consider degree 3:

3 * 3 mod 11 = 9

9 * 3 mod 11 = 5

5 * 3 mod 11 = 4

4 * 3 mod 11 = 1

Order 3 equals 5. It does not “run through” all values. $$$F_ {11} ^ *$because we see that a looping occurs on the fifth power: if we continue multiplication, we again get 3, 9, 5, 4, 1.

What else can be said about 3?

This is also a generator. But not for $$$F_ {11} ^ *$, and for its subgroup consisting of five elements {3, 9, 5, 4, 1}.

It is easy to see that this is a subset $$$F_ {11} ^ *$- subgroup: there is a neutral element 1. Closure: the result of any a * b mod p for these numbers does not go beyond this set, because the result will be one of the set {3, 9, 5, 4, 1}.

Each element has the opposite: 3 * 4 mod 11 = 1, 9 * 5 mod 11 = 1, 1 * 1 mod 11 = 1. What other subgroups are in $$$F_ {11} ^ *$?

There is also a group of order 2: {1, 10}

And of course, the trivial subgroups {1} and {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (since formally the group is a subgroup of itself)

How can I optimize generator search for $$$F_ {11} ^ *$?

Here it is necessary to use the foundation of the theory of groups - the Lagrange theorem: “The order of a subgroup divides the order of a group”.

The element x is either a generator of a group, or is a generator of one of its subgroups. Consequently, raising x to the order of the subgroups and comparing the result with 1 can confirm or refute this.

Back to $$$F_ {11} ^ *$. Thanks to the Lagrange theorem, we can confidently say that there are nontrivial subgroups of only orders 2 and 5, since the order $$$F_ {11} ^ *$equals 10.



Thus, we could reduce the calculations for 2, raising it only to degrees 2 and 5!



$$$2 * 2$mod 11 = 4 ≠ 1

$$$2 ^ 5$mod 11 = $$$2 ^ 2$* $$$2 ^ 2$* $$$2$mod 11 = $$$4 * 4 * 2$mod 11 = 10 ≠ 1 Now these calculations are enough to prove that 2 is a generator $$$F_ {11} ^ *$

Similarly for 4:

4 * 4 mod 11 = 5 ≠ 1 ok, the next step is the fifth degree for 4:

$$$4 ^ 5$mod 11 = $$$4 ^ 2$* $$$4 ^ 2$* 4 mod 11 = 5 * 5 * 4 mod 11 = 100 mod 11 = 1 -> 4 is not a generator $$$F_ {11} ^ *$What if the structure is a bit more complicated? Will consider $$$F_ {19} ^ *$:

Order 18 = 3 * 3 * 2. Dividers 18: 2, 3, 6, 9 Choose a random element, for example 3:

We raise 3 to the power r1 = 18/3 = 6:

$$$3 ^ 6$mod 19 = 7 ≠ 1

We raise 3 to the power r2 = 18/2 = 9:

$$$3 ^ 9$mod 19 = 18 ≠ 1



It is not necessary to build the element under study to the degree of all subgroups, i.e. 2, 3, 6, 9, since if the element turns out to be a generator of a subgroup of a subgroup, then still raising to the power of the order of the subgroup will give 1.



For example, if we chose not 3, but 11, we would stop at the first step:



$$$11 ^ 6$mod 19 = 1.

because 11 has order 3

$$$11 ^ 6$mod 19 = $$$11 ^ {3 * 2}$mod 19 = $$$1 ^ 2$mod 19

3 in $$$F_ {19} ^ *$generates a subgroup {1, 7, 11}



Nontrivial subgroups $$$F_ {19} ^ *$: {1, 18}, {1, 7, 11}, {1, 7, 8, 11, 12, 18}, {1, 4, 5, 6, 7, 9, 11, 16, 17}



But back to DH. In practice, this choice of parameters for it is a large choice (~ $$$2 ^ {3072}$, i.e., length 3072 bits) of prime number p and generator $$$g$order $$$q$which (i.e. the minimum degree that results in 1: $$$g ^ q$mod p = 1) is also a large prime number (~ $$$2 ^ {256}$). The basic operation that is performed in the algorithm is exponentiation x modulo: $$$g ^ x$mod p.

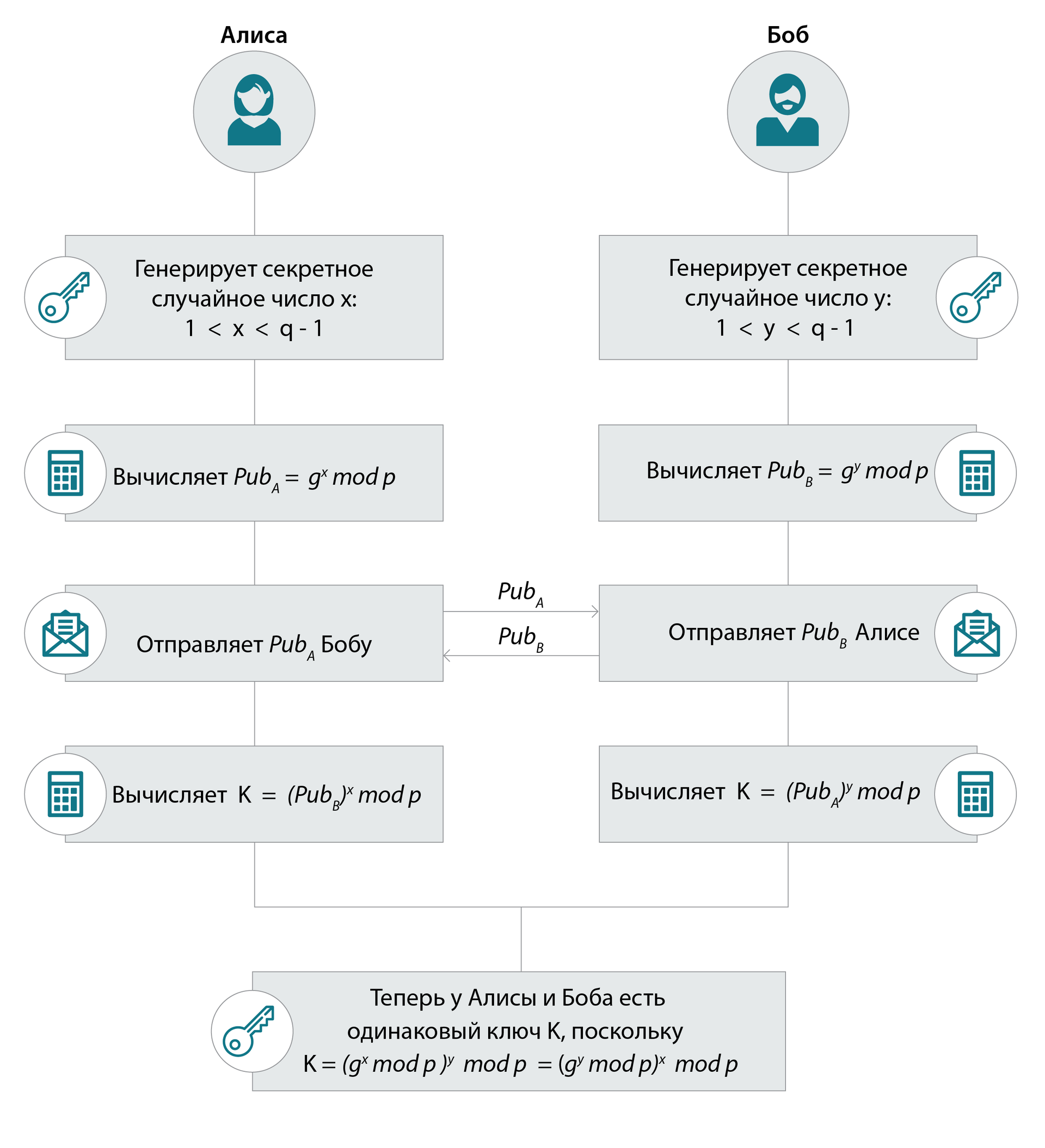
Note: Alice and Bob need to check the keys coming from outside that they belong to the “working” subgroup of a large simple order q:

Alice checks $$$Pub_B ^ q$mod p = 1? If not, the protocol is aborted.

Bob does the same: he checks the key that came from Alice: $$$Pub_A ^ q$mod p = 1?

We are not considering an adversary who could replace public keys on the way, but nevertheless, we must always remember that even in cryptography there are cases from the category “we don’t need enemies with such friends”: the program on Alice or Bob’s devices may contain various errors (in the implementation of modular arithmetic, or memory can simply be damaged).

If the checks were normal, then Alice and Bob consider the keys for symmetric algorithms in order to use them to protect the data transmission channel (for example, to encrypt data and read the MAC (Message Autentication Code) or just read the MAC).



Back to $$$g ^ x$mod p operation is called Discrete Logarithm (DL) or in our Discrete Logarithmization: let p, g and $$$g ^ x$. Required to find the degree of x. This is exactly what is very interesting to the attacker.



Of course, the choice of the group is not personally Alice or Bob, but the cryptographers (although some subsets of all Alice and Bobs belong to their set, but we do not consider this particular case). A subset of cryptographers who have a deep understanding of the structure of groups and know which ones to use safely sometimes publish the results of their work in the form of specific numbers p, g and step-by-step descriptions of algorithms with test vectors. They can be found in the form of NIST or RFC standards.



Here is an example of unsafe parameters for DH: a group of “smooth” order, i.e. whose number of elements can be represented as a product of powers of small primes, since it can easily compute the discrete logarithm using the Pollig-Hellman method, which computes the discrete logarithm in subgroups of a group, and then using the Chinese remainder theorem, obtains the logarithm for the group itself. Since the calculations by the Chinese theorem themselves are fairly simple, the complexity of the entire Pollig-Hellman algorithm can be roughly estimated as the complexity of calculating DL in the largest subgroup of simple order.

Present: Elliptical Diffie-Hellman

In 1985, Neil I. Koblitz and Victor Saul Miller independently discovered each other how to use elliptic curves in cryptography. Their discovery helped to create elliptic variants of the Diffie-Hellman, El-Gamal, MQV, DSS, GOST R 34.10-94 algorithms, which initially used the multiplicative group of a finite field. As a result, new algorithms (with the exception of GOST) received the prefix EC: ECDH, EC ElGamal, ECMQV, ECDSS. And our Russian GOST R 34.10-94 was transformed into GOST R 34.10-2001 (and then more reliable 34.10-2012). Why was such a transition to elliptic curves necessary? He allowed faster calculations with the same level of security.



Alice and Bob choose Domain parameters for elliptic curves.



What are the domain parameters for elliptic curves:



1. Galois field GF ( $$$p ^ n$). Consists of $$$p ^ n$elements, where p -

field characteristic (prime)

(In practice, n = 1 is used more often. Denoted by GF ( $$$p$) and is called

simple field (prime field). Its elements are all numbers from 0 to p-1)



2. Weierstrass equation of a curve over a field GF ( $$$p ^ n$) (“Over the Field” means that

all coefficients (in this case, A and B) and solutions (x and y) are field elements):



$$$y ^ 2$= $$$x ^ 3$+ A $$$x$+ B (for p> 3)



where A and B are such that 4 $$$A ^ 3$+27 $$$B ^ 2$≠ 0, x, y - affine

coordinates



3. The order of a group of points (the number of all its elements)

Denoted as #E (GF ( $$$p ^ n$))

It is represented as q * k, where q (large prime) is the order of the subgroup, and k is small

the number (not necessarily prime) is called cofactor (multiplier)



4. The generator of the subgroup of the group of points of the curve (base point): the point Q, which has order q. (The Pollig-Hellman discrete logarithm algorithm is also applicable to a group of points of an elliptic curve, like any other Abelian group, so a group of points must have a “non-smooth” order. Ie, equal to the product of a large prime number by a small number. Unlike the classic version, the group of which always contains p-1 element, the group of elliptic curves may have a simple order)



Recall the most basic:



Elements of a group are points of a curve, i.e. pairs (x, y) are solutions of the Weierstrass equation. Group operation is called addition of points:



(x1, y1) + (x2, y2) = (x3, y3)



Plus, there is also the so-called Point At Infinity or zero point (but the point at infinity sounds more beautiful, agree) Let’s denote O. This is an analogue unit for the multiplicative group of a finite field (from classical DH): 1 * t mod p = t * 1 mod p = t, for curves: (x, y) + O = O + (x, y) = (x, y). Her fundamental difference from a sister from a multiplicative group is that she cannot be represented as any field element, i.e. as an ordinary point (x, y) so that it is possible to perform calculations with it as with the other points using the general formula.



In the first part of the article we will consider only the simple field GF (p), therefore all examples and formulas use the mod p suffix:



The formula for adding the points (X1, Y1) and (X2, Y2):



X3 = $$$µ ^ 2$- X1- X2 mod p

Y3 = µ (X1 - X3) - Y1 mod p



where µ = (Y2-Y1) / (X2-X1) mod p if X1 ≠ X2:



If X1 = X2 and Y1 = Y2 ≠ 0, then µ = (3 $$${X1} ^ 2$+ A) / 2Y1 mod p



In the case when X1 = X2 and Y1 = - Y2 mod p, then the formulas are not applicable and the result is a point at infinity.



Fractions help to more beautifully express the inverse element in a multiplicative group: for example, $$${(Y2-Y1) / (X2-X1)}$mod p means $$${(Y2-Y1)}$* $$${(X2-X1)} ^ {- 1}$mod p where $$${(X2-X1)} ^ {- 1}$- inverse to the value $$${(X2-X1)}$



Denote the scalar product of the number n by the point Q as follows: [n] * Q.

[n] * Q = Q + Q +… + Q + Q



n times (this is a sequential addition operation performed n times using the above formulas) The attacker knows the domain parameters: the curve and the point Q (the subgroup generator) and the result of multiplying the scalar n by the point Q: [n] * Q. What he wants to find: the number n (ie, solve the ECDLP problem). In which case is it easy? Captain Obvious says that if Q belongs to a small subgroup, then the point [n] * Q will belong to the same subgroup and the attacker will go through all possible scalars and multiply them by Q until he receives the well-known point [n] * Q. Therefore, Q must belong to a subgroup of large simple order.



So, the main group should contain a subgroup of a large simple order (in other words, the order of the whole group should NOT be smooth). Captain Obvious again in the case and reports: in order for the group to contain a large subgroup, it is necessary that the group itself be large. The order of the group of points of the curve E over the field GF ( $$$p ^ n$) is denoted by #E (GF ( $$$p ^ n$)). The Hasse theorem gives a very useful estimate:



#E (GF ( $$$p ^ n$)) = $$$p ^ n$+ 1 - t, where t is the trace of Frobenius, which in absolute value t ≤ 2 * $$$\ sqrt {p ^ n}$. Those. group order #E (GF ( $$$p ^ n$)):

$$$p ^ n$+ 1 - $$$\ sqrt {p ^ n}$≤ #E (GF ( $$$p ^ n$)) ≤ $$$p ^ n$+ 1 + $$$\ sqrt {p ^ n}$



Now we know how the number of field elements is related to the number of points: they practically do not differ in order. Is it possible to say that an attacker needs about the points of the calculation curve to get a scalar? For bruteforce, yes, but there is a more beautiful method that requires much less effort. Pollard's method, which is also applicable to DLP (as well as to any other commutative group). This is a probabilistic algorithm. The number of operations it requires is about the square root of the number of elements of the group. Thus, if we consider “combat” cryptographic curves (cq * k, where q is a large prime number, and k is a small number: in practice 1, 2 or 4), then their security is conveniently evaluated as the number of operations that an attacker must perform when the aid of the most “advanced” method for these curves - the Pollard method.



Example:



The world's most used NIST P-256 curve over a simple field.

The structure of its group is as follows: the order is equal to a large prime number. That is, the order is q * k, where q is simple and cofactor k = 1. Its safety can be assessed as $$$2 ^ {128}$, because today for NIST P-256 nothing better than the Pollard method is invented.



In addition to curves with smooth order, there are others that make it relatively easy to solve ECDLP: supersingular (with a Frobenius trace t such that: t mod p = 0) and anomalous (t = 1). Suppose that the Bob and Alice curve does not fall into any of these bad companies and therefore it is practically impossible to solve the ECDLP for it.







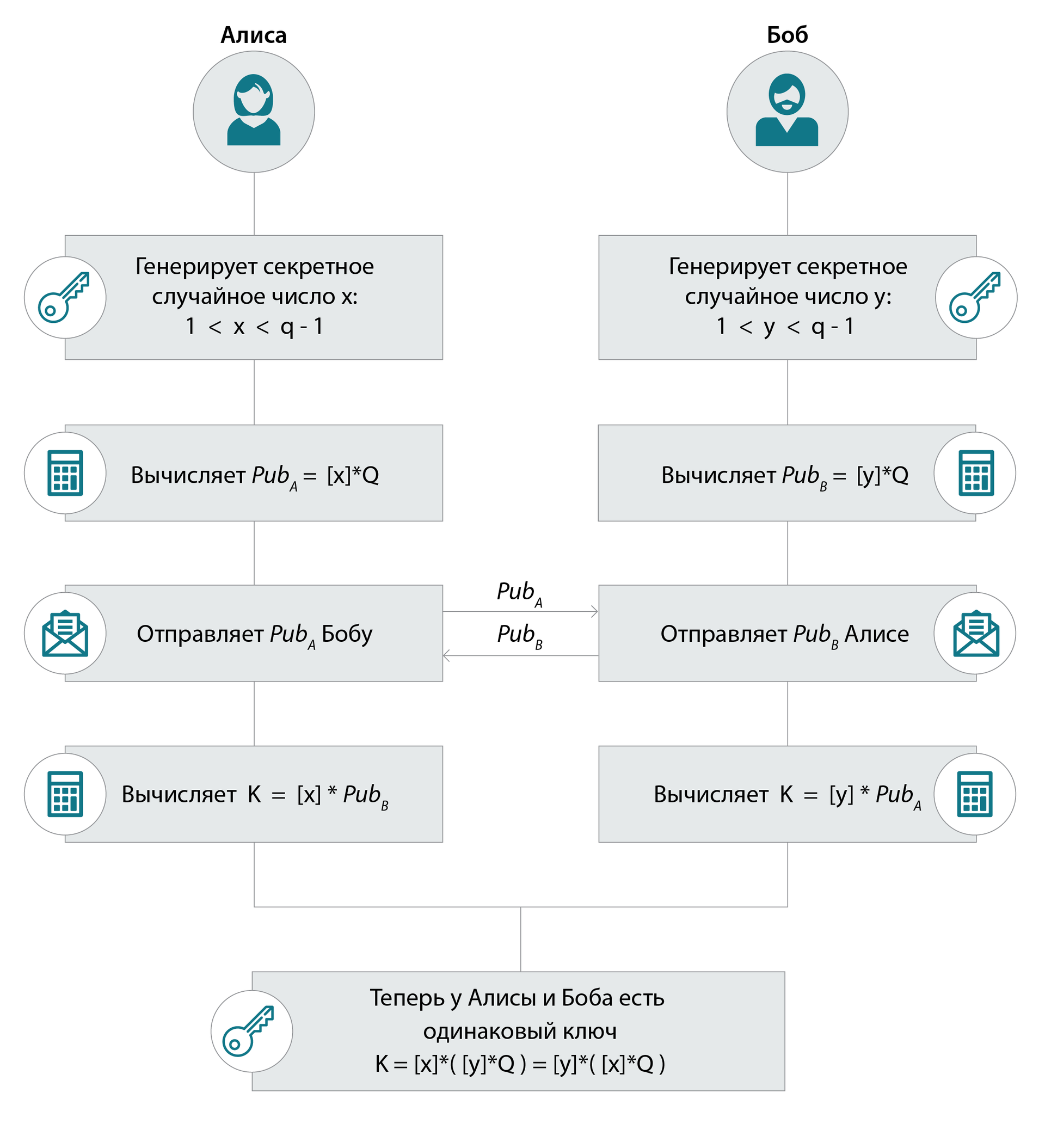
Note: as in the case of classical DH, it is considered good practice to check all (incoming and outgoing) points for belonging to a group, but here the situation is a bit more complicated. First, the coordinates are substituted into the equation - this is a test for joining the group. Then, to check whether a large subgroup of order q belongs to it, we multiply a point by q. If the result is a point at infinity, then everything is OK, and if not, the point lies in some other subgroup and the protocol should be interrupted.



Total:



Classic DH: as a result of key exchange, Alice and Bob have the same element of the group: its generator multiplied by itself x * y times: $$$g ^ {x * y}$mod p



Now copypaste:



Elliptical DH: as a result of key exchange, Alice and Bob have the same element of the group: its generator is a Q point, folded x * y times: [x * y] * Q



The difference in the name of the operations for these groups (addition or multiplication) is not important (after all, the group only has only one operation). So now let's try more universally:

As a result of key exchange, Alice and Bob have the same element of the group: her generator, on which x * y was performed x once a group operation with him.

Quantum nightmare and hate

Classical and elliptical DH besides mathematical elegance unites one unpleasant fact: the complex (for ordinary computers) ECDLP and DLP tasks underlying them can be easily solved if quantum computers are created that are able to keep a sufficiently large number of qubits ( several hundred to several thousand). In addition, this means an end to the RSA cryptosystem: Shor's quantum algorithm allows one to decompose large numbers into prime factors in polynomial time. Therefore, it is for asymmetric algorithms that the post-quantum theme is very relevant. For symmetric ciphers, everything is not so bad yet - they will be attacked by Grover’s quantum algorithm, which has the complexity of the square root of the power of the key set. For example, if you used AES with a key length of 128 bits, then to keep the same security level, you need the same AES, but with a 256 bit key (and AES-128 drops to 64 bit level, that is, the attacker will need to perform $$$2 ^ {64}$operations on a quantum computer).



One of the most promising complex mathematical problems that are resistant to quantum computers is the isogeny of elliptic curves. Read about them in the sequel .



Literature:



Bruce Schneier, Nils Ferguson “Practical Cryptography”

Alfred J. Menezes, Paul C. van Oorschot and Scott A. Vanstone “Handbook of Applied Cryptography”

Lawrence C. Washington “Elliptic Curves: Number Theory and Cryptography, Second Edition”