Introduction to the A * algorithm
When developing games, we often need to find ways from one point to another. We do not just strive to find the shortest distance, we also need to take into account the duration of the movement. Move the asterisk (starting point) and the cross (end point) to see the shortest path. [Approx. Per .: In the articles of this author there are always many interactive inserts, I recommend to go to the original article.]
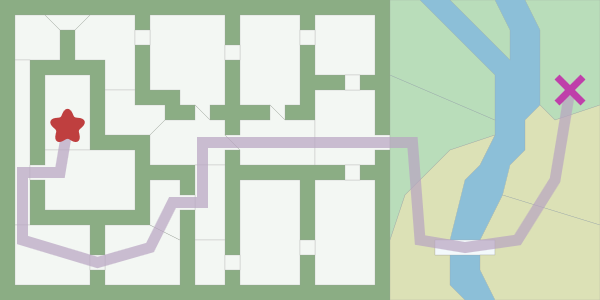
To search for this path, you can use the graph search algorithm, which is applicable if the map is a graph. A * is often used as a graph search algorithm. Search in width is the simplest of the search algorithms for a graph, so let's start with it and gradually move on to A *.
The first thing you need when studying an algorithm is to understand the data . What is served at the entrance? What do we get at the output?
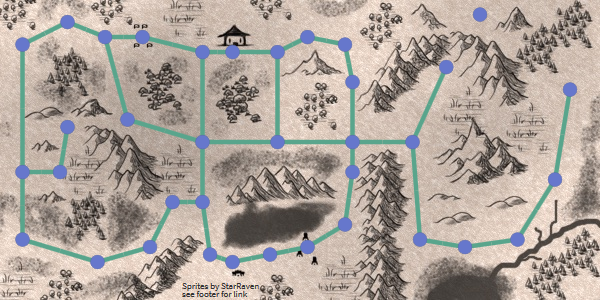
Input : search algorithms for a graph, including A *, receive a graph as input. A graph is a set of points (“nodes”) and connections (“edges”) between them. Here is the graph I gave to A *:
')

A * sees nothing else. He sees only the graph. He does not know whether something is inside or outside, whether it is a door or a room, how large the area is. He sees only the graph! He does not understand any difference between the map above and this one:
Output : A * defined path consists of nodes and edges. Ribs is an abstract mathematical concept. A * tells us to move from one point to another, but does not tell us how to do it. Remember that he does not know anything about rooms or doors, he sees only the graph. You yourself have to decide what the edge of the graph, returned by A *, will be - moving from tile to tile, moving in a straight line, opening the door, running along a curved path.
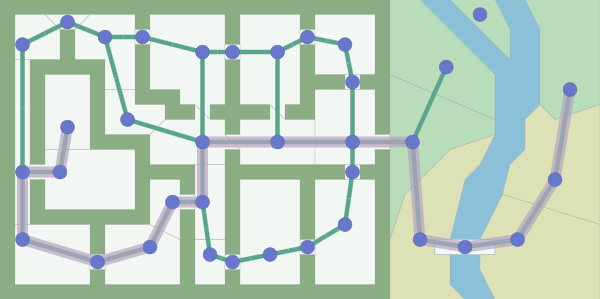
Compromises: for each game card there are many different ways to transfer the path search graph to the A * algorithm. The card in the figure above turns the doors into knots.
And what if we turn doors into ribs?

And if we use the grid to find the way?
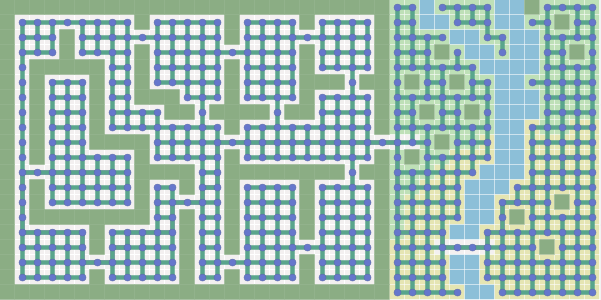
The path search graph does not have to be the same as used in your game map. In the grid-based map, you can use the pathfinding graph without grids, and vice versa. A * runs faster with the least number of nodes in the graph. It is often easier to work with grids, but they make a lot of nodes. This article discusses the A * algorithm itself, and not the design of graphs. More information about the graphs can be found on my other page . For explanations, I will use grids in the future , because it's easier to visualize concepts like this .
There are many algorithms that work with graphs. I will review the following:

A wide search does research evenly in all directions. This is an incredibly useful algorithm, not only for the usual search of a path, but also for procedural map generation, search for paths of flow, distance maps and other types of analysis of maps.

Dijkstra's algorithm (also called equal cost search) allows us to set the priorities for path research. Instead of a uniform study of all possible paths, he prefers low cost paths. We can set reduced costs so that the algorithm moves along the roads, increased cost, to avoid forests and enemies, and much more. When the cost of movement may be different, we use it instead of searching in width.

A * is a modification of the Dijkstra algorithm, optimized for a single end point. Dijkstra's algorithm can find paths to all points, A * finds a path to one point. He gives priority to paths that lead closer to the goal.
I will start with the simplest - search in width, and will add functions, gradually turning it into A *.
The key idea of all these algorithms is that we track the state of the expanding ring, which is called the boundary . In the grid, this process is sometimes called flood fill, but the same technique applies to maps without grids. View the border expansion animation:
How to implement it? Repeat these steps until the border is empty:
Let's take a look at this in more detail. Tiles are numbered in the order of their visit:
The algorithm is described in just ten lines of Python code:
In this cycle is the whole essence of the search algorithms for the graph of this article, including A *. But how do we find the shortest path? The cycle doesn’t really create paths, it just tells us how to visit all the points on the map. It happened because the search in width can be used for much more than just finding paths. In this article, I show how it is used in tower defense games, but it can also be used in distance maps, in procedural map generation and much more. However, here we want to use it to search for paths, so let's change the loop so that we track where we came from for each point visited and rename the
Now came_from for each point indicates the place from which we came. This is similar to the "bread crumbs" from a fairy tale. This is enough for us to recreate the whole path. See how the arrows show the way back to the starting position.
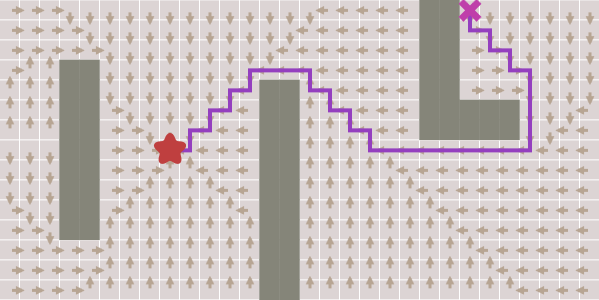
The code for recreating paths is simple: follow the arrows back from the goal to the beginning . A path is a sequence of edges , but sometimes it is easier to store only nodes:
This is the simplest path finding algorithm. It works not only in grids, as shown above, but also in any structure of graphs. In a dungeon, points of a graph can be rooms, and edges - doors between them. In the platformer, the nodes of the graph can be locations, and the edges - possible actions: move left, right, jump, jump down. In general, you can perceive the graph as a state and action, changing the state. Read more about the presentation of the maps I wrote here . In the remainder of this article, I will continue to use the examples with grids, and tell you why you can use search variations in width.
We found paths from one point to all other points. Often we do not need all the paths, we just need a path between two points. We can stop expanding the border as soon as we find our goal. See how the border stops expanding after finding the target.
The code is quite straightforward:
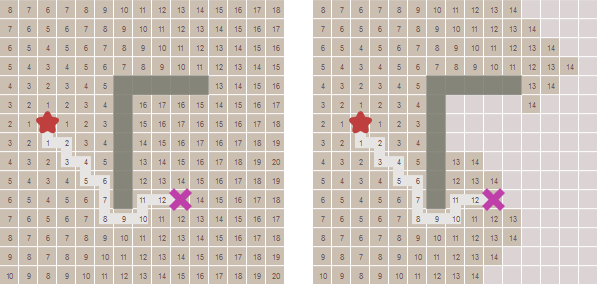
So far we have taken steps with equal value. In some cases, the search for ways in different types of movement has a different cost. For example, in Civilization, movement through plains or desert can cost 1 point of movement, and movement through a forest - 5 movement points. On the map at the very beginning of the article, passing through the water is 10 times more expensive than moving through the grass. Another example is the diagonal movement in a grid, which costs more than movement along the axes. We need to find the way to take this cost into account. Let's compare the number of steps from the beginning with the distance from the beginning:

For this, we need a Dijkstra algorithm (also called a uniform cost search). How does it differ from search in width? We need to track the cost of movement, so we add a new variable,
Using a priority queue instead of a normal queue changes the way the boundary is expanded . Contour lines allow you to see it. Watch the video to see how the border widens more slowly through forests, and the search for the shortest path is performed around the central forest rather than through it:
The cost of movement, which differs from 1, allows us to explore more interesting graphs, not just grids. On the map at the beginning of the article, the cost of movement is based on the distance between the rooms. Movement costs can also be used to avoid or prefer areas based on the proximity of enemies or allies. An interesting implementation detail: the usual priority queue supports inserts and deletes, but in some versions of the Dijkstra algorithm, the third operation also uses the priority of an element that is already in the priority queue. I do not use this operation, and explain it on the implementation page of the algorithm .
In the search in width and Dijkstra algorithm, the border expands in all directions. This is a logical choice if you are looking for a path to all points or to a set of points. However, usually a search is performed for only one point. Let's make it so that the border expands toward the goal more than in other directions. First, we define a heuristic function that tells us how close we are to the goal:
In the Dijkstra algorithm, for ordering the priority queue, we used the distance from the start . In the greedy search for the first best match for the order of the queue with priorities, we instead use the estimated distance to the target . The point closest to the target will be examined first. The code uses a queue with priorities from search to width, but no
Let's see how it works:
Wow! Awesome, right? But what happens on a more complex map?
These paths are not the shortest. So, this algorithm works faster when there are not very many obstacles, but the paths are not very optimal. Can this be fixed? Of course.
Dijkstra's algorithm is good at finding the shortest path, but it spends time researching all directions, even unpromising ones. The eager search explores promising avenues, but may not find the shortest path. Algorithm A * uses both the true distance from the beginning and the estimated distance to the target.
The code is very similar to Dijkstra's algorithm:
Compare algorithms: Dijkstra's algorithm calculates the distance from the starting point. A greedy search for the first best match estimates the distance to the target point. A * uses the sum of these two distances.
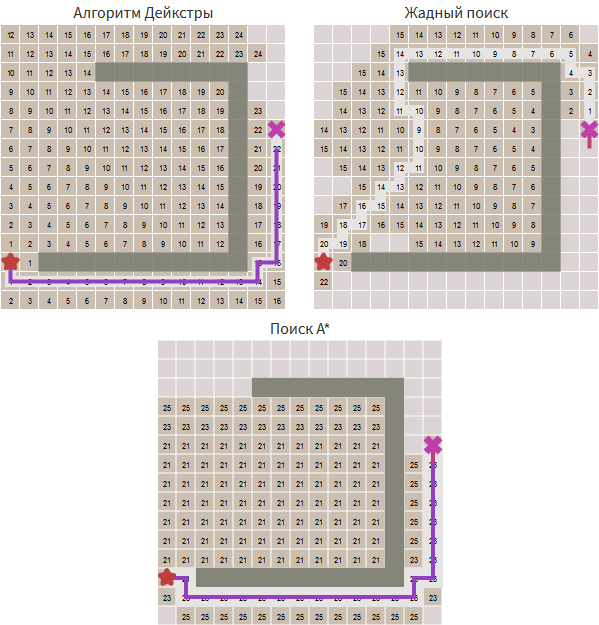
Try to make holes in different places of the wall in the original article. You will find that the greedy search finds the right answer, A * finds it too, exploring the same area. When the greedy first-best search finds the wrong answer (the longer path), A * finds the right one, like Dijkstra's algorithm, but still explores less than Dijkstra's algorithm.
A * takes the best from two algorithms. Since heuristics do not re-estimate distances, A * does not use heuristics to find a suitable answer. It finds the optimal path, like Dijkstra’s algorithm. A * uses heuristics to change the order of nodes to increase the likelihood of an earlier finding a target node.
And that is all! This is the algorithm A *.
Are you ready to implement it? Try using a ready-made library. If you want to implement it yourself, then I have instructions for step-by-step implementation of graphs, queues and path finding algorithms in Python, C ++ and C #.
What algorithm should be used to find the paths on the game map?
What about the best ways? Search in width and Dijkstra's algorithm is guaranteed to find the shortest path in the graph. Greedy search does not necessarily find it. A * is guaranteed to find the shortest path if the heuristics is never greater than the true distance. When heuristics become smaller, A * turns into Dijkstra's algorithm. When heuristics get larger, A * turns into a greedy search for the best first match.
What about performance? It is best to eliminate unnecessary points of the graph. If you are using a mesh, then read this . Reducing the size of the graph helps all graph search algorithms. After that, use the simplest possible algorithm. Simple queues are faster. A greedy search is usually faster than the Dijkstra algorithm, but does not provide optimal paths. For most pathfinding tasks, the best choice is A *.
What about using not on cards? I used maps in the article because I think it is easier to explain the operation of the algorithm. However, these graph search algorithms can be used on any graphs, not only on game maps, and I tried to present the code of the algorithm in a form that does not depend on two-dimensional grids. The cost of movement on the maps turns into arbitrary weights of the edges of the graph. Heuristics are not so easy to transfer to arbitrary maps, it is necessary to create heuristics for each type of graph. For flat maps, distances are a good choice, so we used them here.
I wrote a lot more about finding ways here . Do not forget that searching by graphs is only one part of what you need. By itself, A * does not handle such aspects as joint movement, moving obstacles, changing the map, estimating dangerous areas, formations, turning radii, object sizes, animation, smoothing of paths, and much more.

To search for this path, you can use the graph search algorithm, which is applicable if the map is a graph. A * is often used as a graph search algorithm. Search in width is the simplest of the search algorithms for a graph, so let's start with it and gradually move on to A *.
Map presentation
The first thing you need when studying an algorithm is to understand the data . What is served at the entrance? What do we get at the output?
Input : search algorithms for a graph, including A *, receive a graph as input. A graph is a set of points (“nodes”) and connections (“edges”) between them. Here is the graph I gave to A *:
')

A * sees nothing else. He sees only the graph. He does not know whether something is inside or outside, whether it is a door or a room, how large the area is. He sees only the graph! He does not understand any difference between the map above and this one:

Output : A * defined path consists of nodes and edges. Ribs is an abstract mathematical concept. A * tells us to move from one point to another, but does not tell us how to do it. Remember that he does not know anything about rooms or doors, he sees only the graph. You yourself have to decide what the edge of the graph, returned by A *, will be - moving from tile to tile, moving in a straight line, opening the door, running along a curved path.

Compromises: for each game card there are many different ways to transfer the path search graph to the A * algorithm. The card in the figure above turns the doors into knots.
And what if we turn doors into ribs?

And if we use the grid to find the way?

The path search graph does not have to be the same as used in your game map. In the grid-based map, you can use the pathfinding graph without grids, and vice versa. A * runs faster with the least number of nodes in the graph. It is often easier to work with grids, but they make a lot of nodes. This article discusses the A * algorithm itself, and not the design of graphs. More information about the graphs can be found on my other page . For explanations, I will use grids in the future , because it's easier to visualize concepts like this .
Algorithms
There are many algorithms that work with graphs. I will review the following:

A wide search does research evenly in all directions. This is an incredibly useful algorithm, not only for the usual search of a path, but also for procedural map generation, search for paths of flow, distance maps and other types of analysis of maps.

Dijkstra's algorithm (also called equal cost search) allows us to set the priorities for path research. Instead of a uniform study of all possible paths, he prefers low cost paths. We can set reduced costs so that the algorithm moves along the roads, increased cost, to avoid forests and enemies, and much more. When the cost of movement may be different, we use it instead of searching in width.

A * is a modification of the Dijkstra algorithm, optimized for a single end point. Dijkstra's algorithm can find paths to all points, A * finds a path to one point. He gives priority to paths that lead closer to the goal.
I will start with the simplest - search in width, and will add functions, gradually turning it into A *.
Search wide
The key idea of all these algorithms is that we track the state of the expanding ring, which is called the boundary . In the grid, this process is sometimes called flood fill, but the same technique applies to maps without grids. View the border expansion animation:
How to implement it? Repeat these steps until the border is empty:
- Select and delete a point from the border .
- Mark the point as visited to know that you do not need to process it again.
- Expanding the border, looking at its neighbors . All the neighbors, which we have not yet seen, add to the border .
Let's take a look at this in more detail. Tiles are numbered in the order of their visit:
The algorithm is described in just ten lines of Python code:
frontier = Queue() frontier.put(start ) visited = {} visited[start] = True while not frontier.empty(): current = frontier.get() for next in graph.neighbors(current): if next not in visited: frontier.put(next) visited[next] = True In this cycle is the whole essence of the search algorithms for the graph of this article, including A *. But how do we find the shortest path? The cycle doesn’t really create paths, it just tells us how to visit all the points on the map. It happened because the search in width can be used for much more than just finding paths. In this article, I show how it is used in tower defense games, but it can also be used in distance maps, in procedural map generation and much more. However, here we want to use it to search for paths, so let's change the loop so that we track where we came from for each point visited and rename the
visited to came_from : frontier = Queue() frontier.put(start ) came_from = {} came_from[start] = None while not frontier.empty(): current = frontier.get() for next in graph.neighbors(current): if next not in came_from: frontier.put(next) came_from[next] = current Now came_from for each point indicates the place from which we came. This is similar to the "bread crumbs" from a fairy tale. This is enough for us to recreate the whole path. See how the arrows show the way back to the starting position.

The code for recreating paths is simple: follow the arrows back from the goal to the beginning . A path is a sequence of edges , but sometimes it is easier to store only nodes:
current = goal path = [current] while current != start: current = came_from[current] path.append(current) path.append(start) # optional path.reverse() # optional This is the simplest path finding algorithm. It works not only in grids, as shown above, but also in any structure of graphs. In a dungeon, points of a graph can be rooms, and edges - doors between them. In the platformer, the nodes of the graph can be locations, and the edges - possible actions: move left, right, jump, jump down. In general, you can perceive the graph as a state and action, changing the state. Read more about the presentation of the maps I wrote here . In the remainder of this article, I will continue to use the examples with grids, and tell you why you can use search variations in width.
Early exit
We found paths from one point to all other points. Often we do not need all the paths, we just need a path between two points. We can stop expanding the border as soon as we find our goal. See how the border stops expanding after finding the target.

The code is quite straightforward:
frontier = Queue() frontier.put(start ) came_from = {} came_from[start] = None while not frontier.empty(): current = frontier.get() if current == goal: break for next in graph.neighbors(current): if next not in came_from: frontier.put(next) came_from[next] = current Relocation cost
So far we have taken steps with equal value. In some cases, the search for ways in different types of movement has a different cost. For example, in Civilization, movement through plains or desert can cost 1 point of movement, and movement through a forest - 5 movement points. On the map at the very beginning of the article, passing through the water is 10 times more expensive than moving through the grass. Another example is the diagonal movement in a grid, which costs more than movement along the axes. We need to find the way to take this cost into account. Let's compare the number of steps from the beginning with the distance from the beginning:

For this, we need a Dijkstra algorithm (also called a uniform cost search). How does it differ from search in width? We need to track the cost of movement, so we add a new variable,
cost_so_far , to keep track of the total cost of movement from the starting point. In assessing points, we need to consider the cost of movement. Let's turn our queue into a priority queue. It is less obvious that it may happen that one point is visited several times with different costs, so you need to change the logic a bit. Instead of adding a point to the border in the case where the point has never been visited, we add it if the new path to the point is better than the best previous path. frontier = PriorityQueue() frontier.put(start, 0) came_from = {} cost_so_far = {} came_from[start] = None cost_so_far[start] = 0 while not frontier.empty(): current = frontier.get() if current == goal: break for next in graph.neighbors(current): new_cost = cost_so_far[current] + graph.cost(current, next) if next not in cost_so_far or new_cost < cost_so_far[next]: cost_so_far[next] = new_cost priority = new_cost frontier.put(next, priority) came_from[next] = current Using a priority queue instead of a normal queue changes the way the boundary is expanded . Contour lines allow you to see it. Watch the video to see how the border widens more slowly through forests, and the search for the shortest path is performed around the central forest rather than through it:
The cost of movement, which differs from 1, allows us to explore more interesting graphs, not just grids. On the map at the beginning of the article, the cost of movement is based on the distance between the rooms. Movement costs can also be used to avoid or prefer areas based on the proximity of enemies or allies. An interesting implementation detail: the usual priority queue supports inserts and deletes, but in some versions of the Dijkstra algorithm, the third operation also uses the priority of an element that is already in the priority queue. I do not use this operation, and explain it on the implementation page of the algorithm .
Heuristic search
In the search in width and Dijkstra algorithm, the border expands in all directions. This is a logical choice if you are looking for a path to all points or to a set of points. However, usually a search is performed for only one point. Let's make it so that the border expands toward the goal more than in other directions. First, we define a heuristic function that tells us how close we are to the goal:
def heuristic(a, b): # Manhattan distance on a square grid return abs(ax - bx) + abs(ay - by) In the Dijkstra algorithm, for ordering the priority queue, we used the distance from the start . In the greedy search for the first best match for the order of the queue with priorities, we instead use the estimated distance to the target . The point closest to the target will be examined first. The code uses a queue with priorities from search to width, but no
cost_so_far from Dijkstra’s algorithm is applied: frontier = PriorityQueue() frontier.put(start, 0) came_from = {} came_from[start] = None while not frontier.empty(): current = frontier.get() if current == goal: break for next in graph.neighbors(current): if next not in came_from: priority = heuristic(goal, next) frontier.put(next, priority) came_from[next] = current Let's see how it works:
Wow! Awesome, right? But what happens on a more complex map?
These paths are not the shortest. So, this algorithm works faster when there are not very many obstacles, but the paths are not very optimal. Can this be fixed? Of course.
Algorithm A *
Dijkstra's algorithm is good at finding the shortest path, but it spends time researching all directions, even unpromising ones. The eager search explores promising avenues, but may not find the shortest path. Algorithm A * uses both the true distance from the beginning and the estimated distance to the target.
The code is very similar to Dijkstra's algorithm:
frontier = PriorityQueue() frontier.put(start, 0) came_from = {} cost_so_far = {} came_from[start] = None cost_so_far[start] = 0 while not frontier.empty(): current = frontier.get() if current == goal: break for next in graph.neighbors(current): new_cost = cost_so_far[current] + graph.cost(current, next) if next not in cost_so_far or new_cost < cost_so_far[next]: cost_so_far[next] = new_cost priority = new_cost + heuristic(goal, next) frontier.put(next, priority) came_from[next] = current Compare algorithms: Dijkstra's algorithm calculates the distance from the starting point. A greedy search for the first best match estimates the distance to the target point. A * uses the sum of these two distances.

Try to make holes in different places of the wall in the original article. You will find that the greedy search finds the right answer, A * finds it too, exploring the same area. When the greedy first-best search finds the wrong answer (the longer path), A * finds the right one, like Dijkstra's algorithm, but still explores less than Dijkstra's algorithm.
A * takes the best from two algorithms. Since heuristics do not re-estimate distances, A * does not use heuristics to find a suitable answer. It finds the optimal path, like Dijkstra’s algorithm. A * uses heuristics to change the order of nodes to increase the likelihood of an earlier finding a target node.
And that is all! This is the algorithm A *.
Additional reading
Are you ready to implement it? Try using a ready-made library. If you want to implement it yourself, then I have instructions for step-by-step implementation of graphs, queues and path finding algorithms in Python, C ++ and C #.
What algorithm should be used to find the paths on the game map?
- If you need to find ways from or to all points, use the search in width or Dijkstra's algorithm. Use wide search if the cost of movement is the same. Use the Dijkstra algorithm if the cost of movement changes.
- If you need to find the way to one point, use the greedy search for the best first or A *. In most cases, A * should be preferred. When there is a temptation to use a greedy search, then consider using A * with an “invalid” heuristic .
What about the best ways? Search in width and Dijkstra's algorithm is guaranteed to find the shortest path in the graph. Greedy search does not necessarily find it. A * is guaranteed to find the shortest path if the heuristics is never greater than the true distance. When heuristics become smaller, A * turns into Dijkstra's algorithm. When heuristics get larger, A * turns into a greedy search for the best first match.
What about performance? It is best to eliminate unnecessary points of the graph. If you are using a mesh, then read this . Reducing the size of the graph helps all graph search algorithms. After that, use the simplest possible algorithm. Simple queues are faster. A greedy search is usually faster than the Dijkstra algorithm, but does not provide optimal paths. For most pathfinding tasks, the best choice is A *.
What about using not on cards? I used maps in the article because I think it is easier to explain the operation of the algorithm. However, these graph search algorithms can be used on any graphs, not only on game maps, and I tried to present the code of the algorithm in a form that does not depend on two-dimensional grids. The cost of movement on the maps turns into arbitrary weights of the edges of the graph. Heuristics are not so easy to transfer to arbitrary maps, it is necessary to create heuristics for each type of graph. For flat maps, distances are a good choice, so we used them here.
I wrote a lot more about finding ways here . Do not forget that searching by graphs is only one part of what you need. By itself, A * does not handle such aspects as joint movement, moving obstacles, changing the map, estimating dangerous areas, formations, turning radii, object sizes, animation, smoothing of paths, and much more.
Source: https://habr.com/ru/post/331192/
All Articles