A very rude approach to determining a person’s language (or how to understand a person’s language from a normal corporate base)

What do these pictures, Excel and applied database work have in common? That's right - Bayesian approach to data analysis.

If I didn’t intrigue you with the picture above, then let me tell you just a little about Bayesian networks and how to use them on the knee (and why they are little used in practice). This subject is quite technical (here is a conditionally free course from Stanford, it is a bit boring and very technical, but in the subject. There is still a strange thing - you can complete the course and understand everything in 10 hours, and to solve problems in the lab, you need 50 hours the feeling is that the tasks are the PhD of the course author ...).
')

0. A bit of theory

In a nutshell, in simple terms, Bayesian models are a set of probability distributions (sorry for the terms), which are connected by arrows (it sounds terrible, but the simplest explanation is). In classic Bayesian models, the arrows have a direction (in Markov chains, there is no direction).

There is also a repost link about the visualization of conditional Bayes probability.


Definition from the professor.

If the model is divided into fingers into components, then in essence it consists of:

1. Unconditional probability distributions (the sum of weights in the table is equal to one) of certain random variables (complexity, intelligence, estimates from the example below);
2. Conditional distributions of random variables that depend on others;
3. The rules by which you can work with such models, cause-effect relationships and axiomatics ( see the course above );

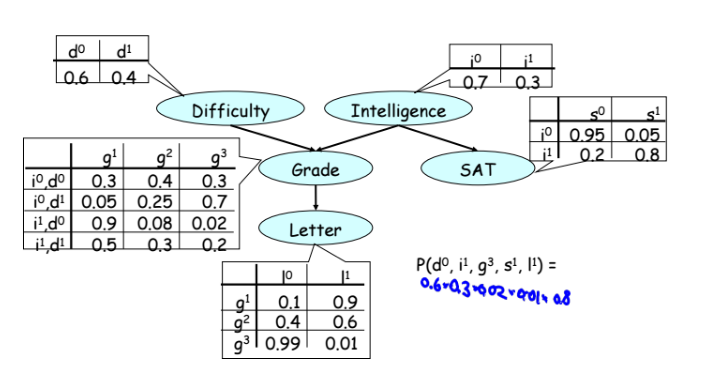
Talk less, work more. Here is an explanation in a nutshell.
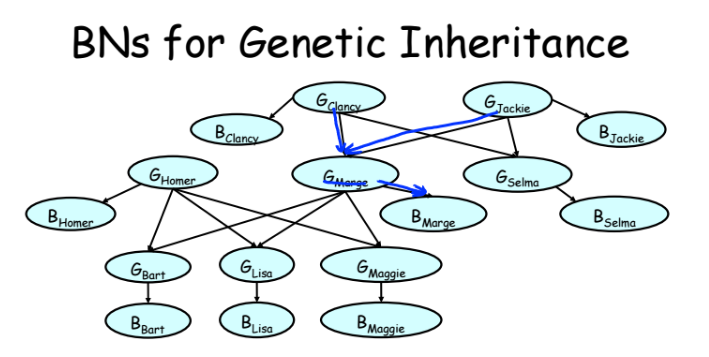
A more complex model on the example of Simson.


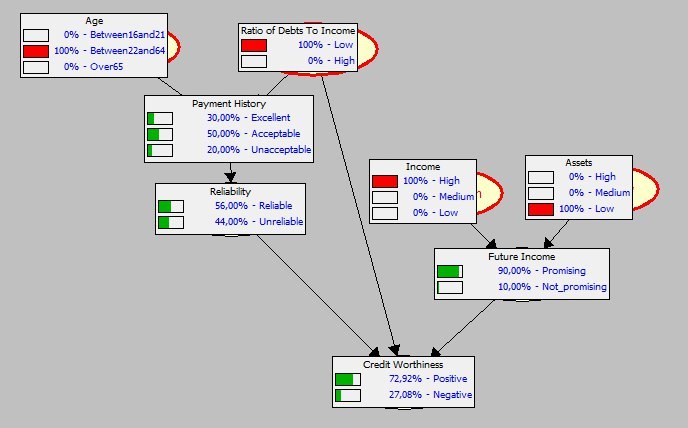
More realistic model

Such models are mathematical in the strict sense and they have their own axiomatics. But from my point of view, it is interesting for them to be able to draw conclusions about variables that are not formally connected in any way. In order not to get into the wilds of what I don’t really understand, I’ll just give 3 examples of how such models can allow you to make the simplest conclusions in real life and then tell you how they helped me solve an applied problem and why they are rarely used in practice .

1. A bit of logic

Example 1 - causation (examples of their course) or induction (in mathematics, arrow to the right =>). The probability that you will have a positive review (letter), ceteris paribus, is approximately 50%. If at the same time you are not very smart, then it drops to 39%. If this course is simple - then the probability again rises to 51%. It all seems simple and logical.


Example 2 - deduction (decision based on some data, or arrow left <=). If a student received a top three, then the likelihood that he is not very smart is growing, and the likelihood that the course is complex is also growing.


Example 3 is the most interesting. If we recorded that a student received a troika, then with an increase in the observed complexity of the subject, the probability that the student is intelligent also begins to grow. It turns out that unrelated variables — the intelligence and complexity of the course become related, provided that we have the observation of the assessment that the student received. In fact, this is just an example of applying the Bayes theorem.

2. A bit of practice

A few more words why such models are rarely used in the PURE form in reality:

• The number of parameters of such a model is very high, and often higher than the number of variables;
• It requires a large amount of statistics on past distributions, which is not in every area of ​​knowledge;
• Often, one cannot observe immediate variables, one can only observe the logs of people's actions. In the model described above, observation of assessment and complexity can replace observation of intelligence, but this is all written in the water with a pitchfork;
• If using a linear model there are statistical tests for significance, and using machine-learning algorithms there is a validation and test sample, then using Bayesian models in fact a priori requires a deep knowledge of the subject area and a lot of data;
• On the other hand, in fact, any regression or neural network, according to its logic, is a simple Bayesian model, where a certain data structure is fixed;

And now let's collect all this in my head and apply this approach on the knee to work with corporate databases. If you are pretty well versed in the subject area and how in reality some variables are connected in it, then ultra-simple Bayesian models on the knee can let you very quickly draw the conclusions you need.

Imagine that there is some kind of database where a company collects 3 things - a name, a person’s mail address and his IP address. 99% of web services can access such statistics. Imagine that a company is global and has no restrictions on the geography of its customers and the task is to determine the language in which each person speaks with a high degree of probability in a very short period of time.

Of course, in an ideal world, one could do this ( I’m writing why it doesn’t fit in brackets ):

1. Write / call parts of clients, asking what language they have (and if you have 2 hours for a task and tens or hundreds of thousands of clients?);
2. Take the banal assumption that the language is equal to the most popular language in the country (and if there are many countries in IP addresses, where 3-4 official languages ​​and languages ​​are used differently by different population groups and professions?);
3. Take the language of the interface that customers have chosen (and if they have not had time to go to the interface yet, and have just registered?);
4. Take the browser language (and what if such a log is also not saved, or simply forgot to save?);

In this case, the so-called " sifting " or the approach consisting in the application of primitive intuitive Bayesian probabilities helps. It looks like this:

1. We select the mail domain from the mail address (aveysov@gmail.com => gmail.com);
2. All brightly national services (such as qqq or 123 in China, mail.ru in Russia, and the like) - very much say that a person speaks the language of the service even despite the name of the person or the country of his last;
3. From the rest, choose national subdomains of the type yahoo.de or simply national domains. The conditional probability that a person speaks German even if he has the last country of call - the USA - is much higher than if he has just the country of call - Germany;
4. From the rest we put down the languages ​​for obvious countries where exactly one state language predominates;
5. There are countries with a large number of languages ​​or simply very multi-ethnic / multilingual countries;
6. In this case, ideally, then we need to find vectors that say how the names are distributed by language, but I quickly could not find such statistics and simply stopped on the most popular language for the country of the remaining users;

3. A little beauty

This is all fine, but how to check now that our primitive model worked? Very simple - look at the names of people with a given language. Language is usually a statistical property of a culture (there are very few people who have 2-3 native languages ​​and nationalities at once). You can just build a vector of probabilities, but you can build beautiful pictures.

Arabic


German


Greek language


Portuguese

Spanish language


Chinese


Slovenian language


Hungarian


French


Hindi


Polish language


Russian language


Czech


And suddenly the English language (the explanation is simple - if you remove the countries of Southeast Asia, then everything rises on its immest)


English without southeast Asia


Something like that. For a couple of hours, without a training set, but with an understanding of the simplest Bayesian models, you can sift any such dataset and get an acceptable result in terms of effort / time / accuracy.