Task: find a triangle with a smaller perimeter
I stumbled upon this task completely by accident. My friend, a year after graduating from the master's program, decided to study again and began to prepare for admission. So something just needs to be repeated and remembered, well, and deal with something new. Here she sat over a task, I passed by. The task seemed very simple (school level), but we need to think a little.
So, the problem considered here sounds like this: given the angle and point inside it. Through this point to hold the segments having ends on the sides of the angle, so that the resulting triangle has the smallest perimeter.

The problem is part of the proof of the Fanyano problem .
')
The first thoughts that come to mind is probably to build perpendiculars (as the shortest distance to the sides). Display the point symmetrically relative and (get the points and ).
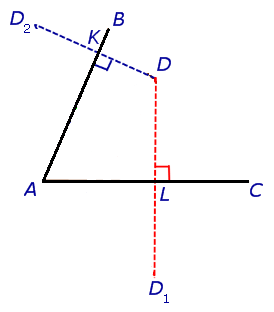
Some may immediately be tempted to connect the intersection points of perpendiculars and sides of an angle. . Then a false impression of “I dodel'e” appears, and it seems that - this is the same triangle.

All wrong. The fact that the two sides of a triangle are the shortest (perpendiculars to a straight line) does not make the perimeter of the triangle minimal.
In fact, the search for a triangle with the smallest perimeter uses the statement: the shortest distance between two points is a straight line. Additional constructions must cause all the lengths of the sides of the desired triangle to be on a straight line. Connect the dots and . Crossing points with the sides of the angle there are the remaining sought vertices of the triangle.
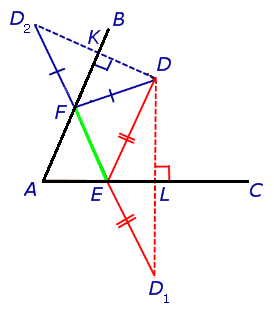
and are medians and heights (dot symmetrically displayed relative to the sides of the angle) of the triangles and accordingly, means triangles and - isosceles. It can be seen that the perimeter of the triangle equal to the length of the segment . A triangle with a smaller perimeter is found.
Take some other points ( and a) on the sides of the corner.
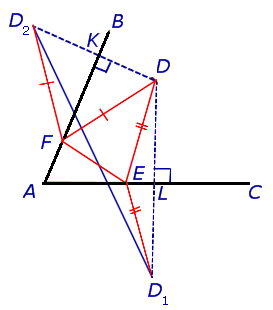
The perimeter of this triangle turns out to be longer than the length of the segment .
That's all. Good luck to all incoming!
So, the problem considered here sounds like this: given the angle and point inside it. Through this point to hold the segments having ends on the sides of the angle, so that the resulting triangle has the smallest perimeter.

The problem is part of the proof of the Fanyano problem .
The task of Fanyano itself sounds as follows:
All sorts of triangles are considered. tops , and which lie on the sides , and acute triangle respectively. Prove that of all triangles DEF the orthocentric triangle of a triangle has the smallest perimeter .
')
Orthocentric Triangle
An orthocentric triangle (ortho-triangle) is a triangle whose vertices are the bases of the heights of the original triangle.
The first thoughts that come to mind is probably to build perpendiculars (as the shortest distance to the sides). Display the point symmetrically relative and (get the points and ).

Some may immediately be tempted to connect the intersection points of perpendiculars and sides of an angle. . Then a false impression of “I dodel'e” appears, and it seems that - this is the same triangle.

All wrong. The fact that the two sides of a triangle are the shortest (perpendiculars to a straight line) does not make the perimeter of the triangle minimal.
In fact, the search for a triangle with the smallest perimeter uses the statement: the shortest distance between two points is a straight line. Additional constructions must cause all the lengths of the sides of the desired triangle to be on a straight line. Connect the dots and . Crossing points with the sides of the angle there are the remaining sought vertices of the triangle.

and are medians and heights (dot symmetrically displayed relative to the sides of the angle) of the triangles and accordingly, means triangles and - isosceles. It can be seen that the perimeter of the triangle equal to the length of the segment . A triangle with a smaller perimeter is found.
Take some other points ( and a) on the sides of the corner.

The perimeter of this triangle turns out to be longer than the length of the segment .
That's all. Good luck to all incoming!
Source: https://habr.com/ru/post/330130/
All Articles