On the issue of numbers
“Well, without a fight? Volleyball - so volleyball! ”
Well, USB is USB.

It is not in my rules to indulge the reader of the KDPV, but I could not resist.
But we begin, as promised, with the time service in the MK. Consider the task associated with this service - there is a set of numbers and among them should be identified those that do not exceed some other preassigned number. Turning to time, we can say that we will need to determine the moment when our current time (T) becomes an interval (I) greater than the origin of the interval (C).
How can we solve this problem, and where is Oroboros?
To begin, we must be able to get the number T, which characterizes the current moment in time (it would be nice to understand exactly how it relates to time, although it is not necessary, to get started, it’s enough to know the size of the number and the behavior of this number as time increases — it increases or decreases ). Next, we must be able to memorize the current T in some variable C (for which it is required that they be of the same type - that’s why we need to know the size). Next, we should be able to associate the desired interval with a certain number of AND (and here we will need knowledge of the exact behavior of T) and we can carry out a simple comparison operation, implementing it in the form
')
T = C + AND
- as soon as this equality is fulfilled, we have reached the point in time we need.
Everything is good, but there is a slippage problem - time flows independently of our behavior, the variable T changes at the same time, and if for some reason we don’t make comparisons at the moment of equality, the condition will be lost and we will never know that the time has come for us (in fact, in the real world we will find out, but more on that later). Therefore, the hard condition = should be replaced by soft> =, or <= if the variable T decreases with time and we get the condition T> = C + AND, which is much more difficult to miss (if at all possible) and everything turns out just fine, it is not clear what will fill the rest of the post.
In fact, this solution has the pitfalls, but they are underwater so that they are not immediately noticed. Consider one of them, which so many times already hit the unwary navigators, which is not counted. And this stone is called a limited width or overflow.
The problem arises due to the fact that time is infinite, and the digit capacity of numbers in the MC is limited and we basically can not stretch an uncountable set to a countable number, this is an axiom. Therefore, our number T, no matter how large it is, cannot uniquely determine a certain moment in time, but will have a period. The duration of this period will be the maximum number, decreasing in T + 1, multiplied by the time of increasing T per unit Pr = (Max + 1) * To. For example, if T is increased by 1 every microsecond, and T is 32 bits wide, then the period will be (2 ^ 32) * 1e-6 = 4 * (2 ^ 10) ^ 3 * 1e-6 ~ 4 * 10 ^ 3 ^ 3 * 1e-6 = 4 * 10 ^ (9-6) = 4000 seconds, which is just over an hour. If T increases by 1 every millisecond, then the period will increase a thousand times and will be 4-6 seconds, that is, approximately 46 days. Of course, the second value is much larger than the first, but they both fade in comparison with eternity.
And what happens when our number reaches its maximum value - different options are possible: it can “lie on the stops” and remain unchanged (but then we lose the ability to fix the continuation of the passage of time), it can begin to decrease (imitating the work of the pendulum, but then computational complexity) and can take the minimum value, usually it is zero (the latter phenomenon is called overflow).
As you can increase the time interval after which this phenomenon will occur - you need to increase any of the factors, but increasing the first will entail complication of operations on working with the number T, and increasing the second will make it impossible to work with intervals less than the minimum step, which is not always acceptable. Therefore, the choice of pitch and digit capacity is always a compromise, which allows not to overstate the requirements for the MK and not to reduce the usability of the work.
There is another way to extend the period - to make the relationship between time and number T non-linear, best (and quite easily realizable on MC) a power function with a power less than one or a logarithm (piecewise linear approximation) fits, but this option is more theoretical interest, rather than a real solution, since the increment step and, accordingly, the accuracy increase with time, which is unacceptable for us.
So what threatens us with the periodicity of T values and the overflow (wraparound, recount, reroll, warp) associated with this - that the monotony of T's behavior is broken, that is, some next time point can be represented by a number not larger than the previous one (if we have T increases with time), and smaller and, accordingly, our formula will stop working, and manifestations of this will be very unpleasant - the program will form a time interval significantly smaller than expected.
Here is a picture that should be kept in mind for understanding what is happening.
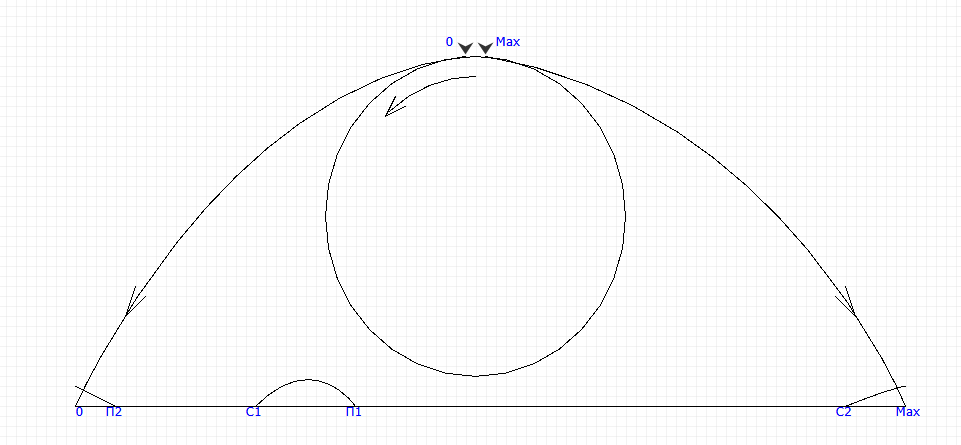
Consider an example of this, for brevity, we assume that T is placed in a byte and its maximum value is 255. If the initial time for forming the interval is C = 20, and the interval is And = 08, then, according to our formula, the time will expire from 28 that is correct, but in the case of C = 250, the condition 251> = (250 + 8) = 258 - 256 = 2 will already be met at T = 251, which is clearly not in line with our expectations. This will not happen too often, near the end of the period, and if you are absolutely sure that your device will never work so long, you can ignore this feature and use the previously proposed formula to track the time intervals that many library authors do. I am categorically opposed to this practice for two reasons - firstly, one should always do the program correctly so that bad habits do not arise, and secondly, it is completely easy to do correctly.
To get the right formula (true in any case), it is necessary to subject the original T> = C + AND to a simple transformation and subtract C from both parts, getting a new condition T - C> = I. From the point of view of mathematics, these conditions are equivalent, but mathematics works with ideal numbers that have an infinite width, although it is not at all helpless and in the case of limited numbers, you just need to impose appropriate conditions. So, taking into account these conditions, our new formula always works correctly. Of course, it is true in the case when T is more than C, but it works and when T is less than C, and this happens because of the remarkable property of subtraction. Imagine T as
T = C + D, where D is an additive in relation to the start, even if during this addition we could get an overflow and then the value T = C + D - Max <S, in any case, our formula turns into
(C + D) - C = C - C + D = D
that is, we get the time interval we are looking for (or rather, the number that characterizes it) for any C and T. Why it happens that way - this is ordinary street magic, that is, the transition from the absolute to the relative coordinate system with the beginning at point C.
The computational complexity of the original formula has one addition and one comparison, one subtraction and one comparison are modified, that is, they do not differ (addition, subtraction and comparison have the same complexity), so why not use the correct one, since it costs nothing. The only limitation of this method should be noted - we cannot order an interval equal to or greater than the maximum representable, that is, we can order, but we will get a much smaller interval, and this is very bad, although it is obvious. And one more, less obvious limitation - if we order an interval close to the maximum possible, there will be very few control points where the condition is met, and if we miss them, then we will go to the second round, and so on. But even in this case, we are guaranteed that we will receive, at a minimum, what we have ordered, which is much better than nothing.
So, we have created an absolutely correct method of counting time intervals, which works in all possible situations (of course, with these limitations in mind), but, as we know, there is no limit to perfection. Let's take a closer look at the resources involved in this method - we need to remember two variables and we need to perform two operations like addition. To reduce resource requirements, you need to return to the original formula.
T> = C + AND
and pay attention to the fact that both quantities in the right part are known at the moment of the beginning of the interval formation and it is possible to calculate the moment of the end of the delay
= + ,
and the formula will turn into expression
T> = P.
Unfortunately, its main drawback - the false triggering at overflow, remains in force, but we can go the tried and tested way and use the subtraction T - P> = 0.
Unfortunately, ordinary street magic has let us down (the fakir was drunk and the focus did not succeed), since this condition is always fulfilled, since the difference between any two numbers is a number from 0 to Mach and is always not less than zero. Actually, the result is predictable, since for two arbitrary numbers it is completely impossible to determine which of them precedes the other from the word “absolutely” is impossible.
Let us try to create an additional criterion and assume that T precedes if (T - ) <(<- T). Not bad for a start, but a direct calculation using this formula will require three subtractions - we will reduce it. First of all we establish the indisputable fact that (T - P) + (P - T) = 0 = Mach + 1.
From this obvious fact we can deduce that T - P will be greater than P - T in the case, and only if T - P> = (Max + 1) / 2. Since the second expression is quite obviously constant and will be calculated at the compilation stage, the resulting condition P - T> = (Max + 1) / 2 requires only two subtraction operations, and we have already reduced the memory by one storage unit, but we can go further.
Note that for the fulfillment of the latter condition, it is required that the most significant bit of the result be set, and we could use conditional jump commands for the value of the result bit, but they are far from being in every MC and the translator can use them not efficiently enough. Fortunately, it is for working with the high bit that any MC has such commands and any translator implements them very well - commands for checking the sign of the number. The fact is that, if we consider the result as a number in the additional code, then the sign is encoded in the most significant bit and checking that the most significant bit of the number contains one, and that the number is negative, coincide. Therefore, our comparison condition can be written as T - P <0.
Let's pay attention to the fact that we perform the subtraction operation with no significant numbers and only interpret the result as a significant number during the comparison operation. This circumstance must be taken into account when writing software that implements this algorithm, for example, for the C language, the corresponding fragment can be executed as follows:
if ( (long) ( - ) < 0) ....So, we need to remember only one number (P) and the computational complexity of the test is one subtraction operation (comparison will use its result and does not require additional operations), it is hardly possible to achieve the best indicators. What we had to pay for such beauty - we now can not order an interval of more than half the maximum possible number, or rather, we can order, but it will stop instantly, so you decide whether it is worth winning such a limit. In Linux systems, the last option is adopted, and the fact that the details are hidden behind the macro is syntactic sugar.
Well, and finally, a little to the side - I discovered recently (actually long ago, just forgot) that I personally cannot call the behavior of the C compiler (at least some of them) logical. For example, the following program fragment behaves completely differently than I would like:
typedef unsigned char Timet;
Timet S = 0xF8, I = 12, T = S + I + 2;
// , MISRA, , , ,
if ( (T - S) >= I) printf ( "time"); //
register Timet D = (T - S);
if (D >= I) printf ("time"); //It is completely incomprehensible to me why, in this form, I see only one message about the expiration of time, and if I change the Timet type to unsigned long, I get two messages. That is, I, of course, dissemble, I understand why this is happening, I do not understand why this decision was made when implementing the compiler. But, by the way, this problem is practically solved very easily - you enable MISRA support (rule 10.1.b) and get the ban on using the unsuccessful string and we have to do everything correctly, that is, reliably, we will simply be forced to write an intermediate assignment. Moreover, this assignment does not cost anything and a good compiler will make a very effective code. Yes, this is a crutch, “but it works,” unfortunately, there is simply no other solution.
I must say that the following code fragment looks even more amusing.
if ( (c = uc ) == uc) printf ( "is equal");during the execution of which you will not receive, quite reasonably, the expected message of equality for some values of the variable uc, and we will not get "what is the worst thing, no
Source: https://habr.com/ru/post/330094/
All Articles