Monte Carlo and tic-tac-toe tree search

So it turned out that to get a programming machine, poor first-timers were given one interesting task: to write a program that searches for a tree using the Monte-Carlo method.

Of course, it all started with searching for information on the Internet. In the great and mighty Russian language there were only a couple of articles from Habr, verbally explaining the essence of the algorithm, and an article from Wikipedia that redirects to the problem of the game of Go and the computer. For me, this is a good start. Google in English for completeness and stumble on an English article from Wikipedia, in which the algorithm is also explained verbally.

Some theory

The Monte Carlo method for searching a tree has been used for a long time in games for artificial intelligence. The task of the algorithm is to choose the most advantageous scenario. A tree is a structure in which, in addition to the move and pointers, there is the number of games played and the number of games won. Based on these two parameters, the method selects the next step. The following image clearly demonstrates how the algorithm works:

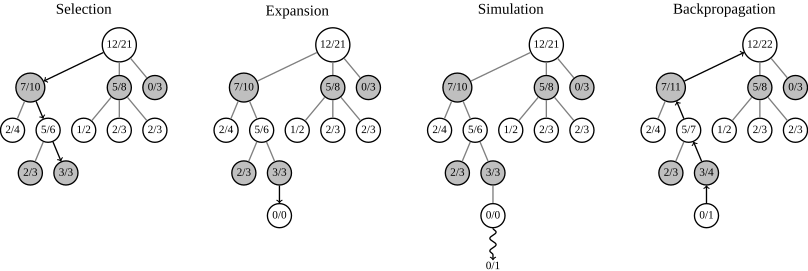
Step 1: Select - Selection. At this step, the algorithm chooses its opponent’s move. If there is such a move, we will choose it, if not, we will add it.
Step 2: Expansion - Expansion. To the selected node with the opponent's move, we will add a node with its own move and with zero results.
Step 3: Simulation - Simulation. Play the game from the current state of the playing field to anyone's victory. From here we take only the first move (i.e. your move) and the results.
Step 4: Back Propagation - Back Propagation. We will distribute the results from the simulation from the current to the root. To all parent nodes we will add one to the number of games played, and if we run into the winner’s node, we’ll add one to the number of games won in such a node.

As a result, a bot with such an algorithm will make winning moves for it.

Actually, the algorithm is not so complicated. Rather, voluminous.

Implementation

I decided to implement the algorithm as a bot for the game Tic-tac-toe. The game is simple and is an excellent example. But the devil is in the details ...

The problem is that we have to play the game on the simulation step without a real player. It was possible, of course, to force the algorithm to do random moves in such simulations, but I wanted some meaningful behavior.

Then the simplest bot was written that could only do two things - interfere with the player and make random moves. To simulate this was more than enough.

Like everyone else, the bot with the algorithm had information about the current state of the field, the state of the field from the last turn, its own move tree and the currently selected node in this tree. To begin with, I will find a new opponent move.

// 0. add node with new move. bool exist = false; int enemyx = -1, enemyy = -1; this->FindNewStep ( __field, enemyx, enemyy ); for ( MCBTreeNode * node : this->mCurrent->Nodes ) { if ( node->MoveX == enemyx && node->MoveY == enemyy ) { exist = true; this->mCurrent = node; } } if ( !exist ) { MCBTreeNode * enemymove = new MCBTreeNode; enemymove->Parent = this->mCurrent; enemymove->MoveX = enemyx; enemymove->MoveY = enemyy; enemymove->Player = (this->mFigure == TTT_CROSS) ? TTT_CIRCLE : TTT_CROSS; this->mCurrent->Nodes.push_back ( enemymove ); this->mCurrent = enemymove; } 

As you can see, if there is such an opponent move in the tree, then we will select it. If not, add.

  // 1. selection // select node with more wins. MCBTreeNode * bestnode = this->mCurrent; for ( MCBTreeNode * node : this->mCurrent->Nodes ) { if ( node->Wins > bestnode->Wins ) bestnode = node; } 

Here we make a choice.

  // 2. expanding // create new node. MCBTreeNode * newnode = new MCBTreeNode; newnode->Parent = bestnode; newnode->Player = this->mFigure; this->mCurrent->Nodes.push_back ( newnode ); 

Expand the tree.

  // 3. simulation // simulate game. TTTGame::Field field; for ( int y = 0; y < TTT_FIELDSIZE; y++ ) for ( int x = 0; x < TTT_FIELDSIZE; x++ ) field[y][x] = __field[y][x]; Player * bot1 = new Bot (); bot1->SetFigure ( (this->mFigure == TTT_CROSS) ? TTT_CIRCLE : TTT_CROSS ); Player * bot2 = new Bot (); bot2->SetFigure ( this->mFigure ); Player * current = bot2; while ( TTTGame::IsPlayable ( field ) ) { current->MakeMove ( field ); if ( newnode->MoveX == -1 && newnode->MoveY == -1 ) this->FindNewStep ( field, newnode->MoveX, newnode->MoveY ); if ( current == bot1 ) current = bot2; else current = bot1; } 

Let's play the game between the bots. I think here we need to explain a little: the field is copied to the current state and the bots play on this copy, the second bot goes first and we will remember its first move.

  // 4. backpropagation. int winner = TTTGame::CheckWin ( field ); MCBTreeNode * currentnode = newnode; while ( currentnode != nullptr ) { currentnode->Attempts++; if ( currentnode->Player == winner ) currentnode->Wins++; currentnode = currentnode->Parent; } 

And the last: we will receive result and we will extend it upwards on a tree.

  // make move... this->mCurrent = newnode; TTTGame::MakeMove ( __field, this->mFigure, mCurrent->MoveX, mCurrent->MoveY ); 

And at the end we just make a move and set our new node from the second step as the current node.

Conclusion

As you can see, the algorithm is not so scary and complicated. Of course, my implementation is far from ideal, but it shows the essence and some practical application.

The full code is available on my GitHub .

All good.