Three cycles in the Lorenz attractor

Studying foreign literature, I stumbled upon the work [1, 2] of the University of Michigan Divakar Viswanath [1, 2] about an iterative algorithm for calculating periodic orbits of dynamic systems based on the Lindstedt-Poincaré (LP) method (I recommend the book [3 , pp. 408-411] ). The advantage of this method is that it does not require numerical integration of the differential equation, therefore it can be applied to the construction of unstable cycles.

Today in mathematics one of the most popular areas of research is the theory of dynamic chaos. The most famous object here is the Lorentz system, introduced in the 60s of the 20th century. I note that since that time many non-linear mathematical models have appeared, where chaotic behavior of solutions takes place, in various fields of science . A few years ago, chaotic systems with no equilibrium positions used to encrypt signals (see, for example, [4]) became popular. Those who are just beginning to study the theory of chaos, I advise you to watch the mathematical film CHAOS , consisting of nine chapters.

Warwick Tucker (Warwick Tucker) is considered to have solved Smale’s 14th problem in [5] using interval arithmetic, but I couldn’t find convincing evidence of the cycles found in the numerical experiments of various authors.
')
Let x (t), y (t) and z (t) be the phase coordinates of the Lorentz system. In 2004, Vishwanat in [2] found three cycles by the LP method. He cited the values ​​of the initial conditions and period:



where T is the period.

In my opinion, this is a significant breakthrough in the study of the Lorenz attractor.

The question may arise - why are 99 digits in the fractional part of numbers? The fact is that periodic orbits are unstable (and these numbers, most likely, are irrational), and in order to construct them by numerical methods on a period with acceptable accuracy, you need to have a large number of decimal places.

I decided to check and build the Vishwanat cycles in the program given in topic [6] (the numerical scheme is also described in [7]). For this, the accuracy of 1e-110 was taken according to the power series, the number of bits under the mantissa of a real number was 390 (machine epsilon is 7.93107e-118), and the passage in time is only forward. The following equations were checked:

x (0) = x (T),
y (0) = y (T),
z (0) = z (T).

For the first cycle, all the signs in the fractional part of all coordinates coincided, except for the last sign for y (T) (I got the number 6), for the second - 80 characters, for the third - 38 characters.

The following are pictures of Vishwanath cycles.





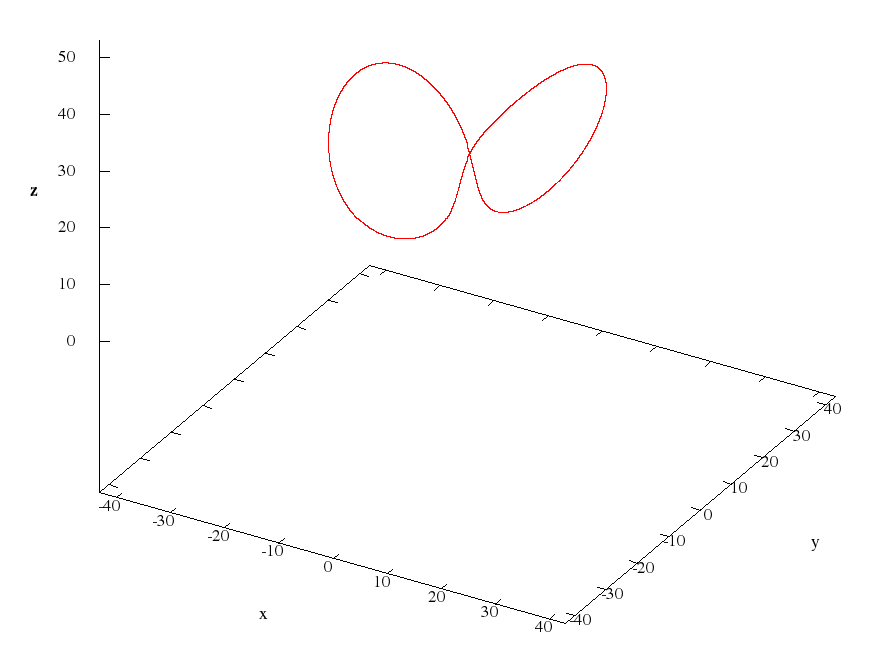
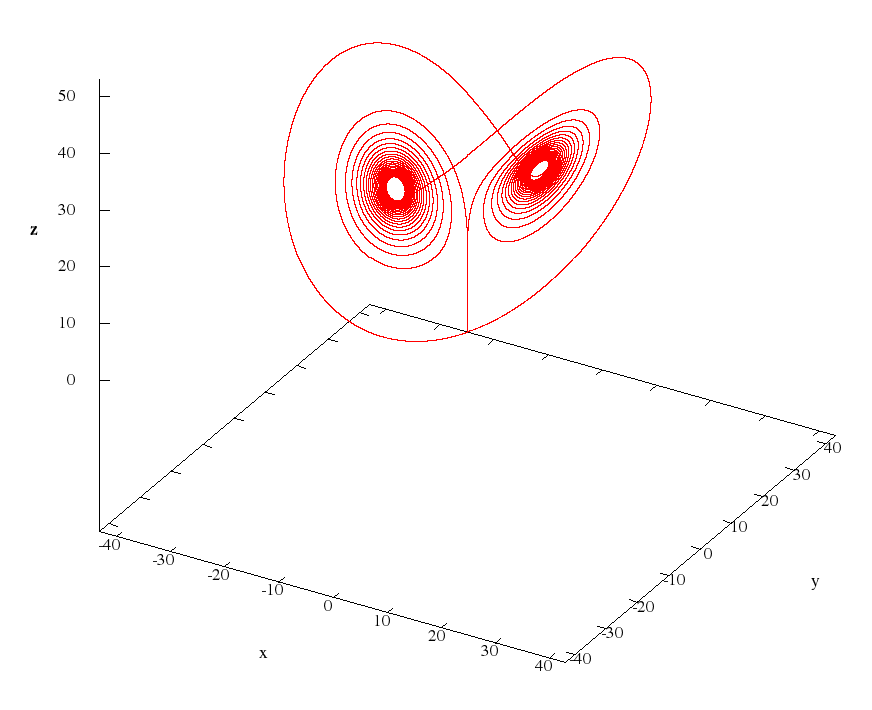
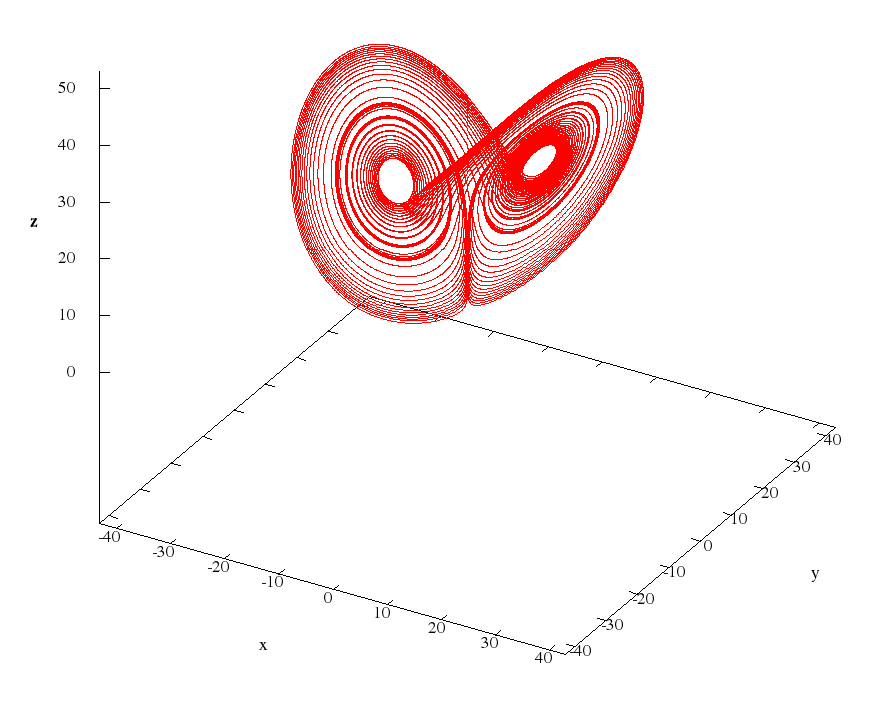
And the animation uploaded to YouTube.


For the second drawing, I was interested in how close the trajectory of the system goes to the origin O (0; 0; 0). A point with coordinates was found in a numerical experiment.



Since the base method for the numerical scheme is the power series method, for the third cycle, the maximum degree of the approximating polynomial is determined at variable integration steps, where the solution is expanded into series, 78, the approximate maximum value of the integration step is 0.0120621. Since the value of T here is quite large, the computation time on my computer was approximately 6.2 minutes.