Breaking words into elements of the periodic table

(The full source code is here )
Sitting in a five-hour class in chemistry, I often glanced at the periodic table hanging on the wall. To pass the time, I began to look for words that I could write using only the notation of the elements from the table. For example: ScAlS, FeArS, ErAsURe, WAsTe, PoInTlEsSnEsS, MoISTeN, SALMoN, PuFFInEsS.
Then I thought what the longest word could be made (I managed to pick up TiNTiNNaBULaTiONS ), so I decided to write a Python program that would search for words consisting of chemical symbols. She had to receive the word and return all of its possible transformations into sets of chemical elements:
Generate naming groupings
If the designations of all elements were of the same length, the problem would be trivial. But some designations consist of two symbols, some - of one. This greatly complicates matters. For example, pu in amputations may mean plutonium (Pu) or phosphorus with uranium (PU). Any input word must be broken down into all possible combinations of one and two-character symbols.
I decided to call such transformations “groups”. They define the specific division of the word into symbols. Grouping can be represented as a tuple of ones and twos, where 1 is a one-character symbol, and 2 is a two-character one. Each division into elements corresponds to a grouping:
- 'AmPuTaTiONS'
(2,2,2,2,1,1,1)
- 'AmPUTaTiONS'
(2,1,1,2,2,1,1,1)
Analyzing the task, in an attempt to find patterns, I wrote such a table in a notebook.
Question: is a string given, n, how many sequences of units and twos can exist for it, so that the number of digits in each sequence equals n?
| n | # groupings | Groupings |
|---|---|---|
| 0 | one | () |
| one | one | (1) |
| 2 | 2 | (1,1), (2) |
| 3 | 3 | (1,1,1), (2,1), (1,2) |
| four | five | (1,1,1,1), (2,1,1), (1,2,1), (1,1,2), (2,2) |
| five | eight | (1,1,1,1,1), (2,1,1,1), (1,2,1,1), (1,1,2,1), (1,1,1,2), (2,2,1), (2,1,2), (1,2,2) |
| 6 | 13 | (1,1,1,1,1,1), (2,1,1,1,1), (1,2,1,1,1), (1,1,2,1,1), (1,1,1,2,1), (1,1,1,1,2), (2,2,1,1), (2,1,2,1), (2,1,1,2), (1,2,2,1), (1,2,1,2), (1,1,2,2), (2,2,2) |
| 7 | 21 | (1,1,1,1,1,1,1), (2,1,1,1,1,1), (1,2,1,1,1,1), (1,1,2,1,1,1), (1,1,1,2,1,1), (1,1,1,1,2,1), (1,1,1,1,1,2), (2,2,1,1,1), (2,1,2,1,1), (2,1,1,2,1), (2,1,1,1,2), (1,2,2,1,1), (1,2,1,2,1), (1,2,1,1,2), (1,1,2,2,1), (1,1,2,1,2), (1,1,1,2,2), (2,2,2,1), (2,2,1,2), (2,1,2,2), (1,2,2,2) |
Answer: fib(n + 1) !?
I was surprised to find the Fibonacci sequence in such an unexpected place. During the following explorations, I was surprised even more when I learned that this pattern was known two thousand years ago. Prosodist poets from ancient India discovered it by exploring the transformations of short and long syllables of Vedic chants. You can read about this and other excellent studies in the history of combinatorics in Chapter 7.2.1.7 of the book The Art of Computer Programming by Donald Knut.
I was impressed with this discovery, but still did not reach the initial goal: generating the factions themselves. After some thoughts and experiments, I came up with the simplest solution I could come up with: generate all possible sequences of ones and twos, and then filter out those whose sum of elements does not coincide with the length of the input word.
from itertools import chain, product def generate_groupings(word_length, glyph_sizes=(1, 2)): cartesian_products = ( product(glyph_sizes, repeat=r) for r in range(1, word_length + 1) ) # , groupings = tuple( grouping for grouping in chain.from_iterable(cartesian_products) if sum(grouping) == word_length ) return groupings A Cartesian product is a collection of all tuples composed of an existing set of elements. The standard Python library provides the function itertools.product() , which returns the Cartesian product of elements for a given iterable. cartesian_products is a generating expression that collects all possible transformations of elements into glyph_sizes up to the length specified in word_length .
If word_length is 3, then cartesian_products generate:
[ (1,), (2,), (1, 1), (1, 2), (2, 1), (2, 2), (1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2) ] The result is then filtered so that the groupings include only those transformations whose number of elements satisfies the word_length .
>>> generate_groupings(3) ((1, 2), (2, 1), (1, 1, 1)) Of course, there is a lot of extra work. The function has computed 14 transformations, but only 3 remain. Performance drops dramatically with increasing word length. But we will come back to this later. In the meantime, I got a working function and moved on to the next task.
Matching words with groupings
After calculating all possible groupings for the word, it was necessary to “match” it with each of the groups:
def map_word(word, grouping): chars = (c for c in word) mapped = [] for glyph_size in grouping: glyph = "" for _ in range(glyph_size): glyph += next(chars) mapped.append(glyph) return tuple(mapped) The function treats each designation in the grouping as with a cup: first it fills it with as many characters from the word as it can, and then proceeds to the next. When all characters are placed in the correct notation, the resulting matching word is returned as a tuple:
>>> map_word('because', (1, 2, 1, 1, 2)) ('b', 'ec', 'a', 'u', 'se') After matching, the word is ready for comparison with the list of symbols of chemical elements.
Search for spelling options
I wrote a spell() function that brings together all previous operations:
def spell(word, symbols=ELEMENTS): groupings = generate_groupings(len(word)) spellings = [map_word(word, grouping) for grouping in groupings] elemental_spellings = [ tuple(token.capitalize() for token in spelling) for spelling in spellings if set(s.lower() for s in spelling) <= set(s.lower() for s in symbols) ] return elemental_spellings spell() gets all the possible spellings and returns only those that are entirely composed of the element designations. For effective filtering of unsuitable options, I used sets.
Python sets are very similar to mathematical sets. These are unordered collections of unique items. Behind the scenes, they are implemented as dictionaries (hash tables) with keys, but without values. Since all elements of the set are hashable, the membership test works very efficiently ( on average, O (1) ). Comparison operators are reloaded to test for subsets using these effective affinity checks. Sets and dictionaries are well described in the wonderful book Fluent Python by Luciano Ramalho.
I earned the last component, and I got a functioning program!
>>> spell('amputation') [('Am', 'Pu', 'Ta', 'Ti', 'O', 'N'), ('Am', 'P', 'U', 'Ta', 'Ti', 'O', 'N')] >>> spell('cryptographer') [('Cr', 'Y', 'Pt', 'Og', 'Ra', 'P', 'H', 'Er')] The longest word?
Satisfied with my implementation of the core functionality, I called the Stoichiograph program and made a wrapper for it using the command line. The wrapper takes a word as an argument or from a file and displays spellings. Adding the function of sorting words in descending order, I set the program on the word list.
$ ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english NoNRePReSeNTaTiONaL NoNRePReSeNTaTiONAl [...] Fine! I myself would not have found this word. The program is already solving the task. I played around and found a longer word:
$ ./stoichiograph.py nonrepresentationalisms NoNRePReSeNTaTiONaLiSmS NONRePReSeNTaTiONaLiSmS NoNRePReSeNTaTiONAlISmS NONRePReSeNTaTiONAlISmS Interesting. I wanted to find out if this is really the longest word ( spoiler ), and I decided to explore longer words . But first it was necessary to deal with performance.
Solving performance problems
Processing 119,095 words (many of which were rather short) took about 16 minutes for the program:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english [...] real 16m0.458s user 15m33.680s sys 0m23.173s On average about 120 words per second. I was sure that you could do it much faster. I needed more detailed performance information to figure out where to dig.
Line profiler is a tool for determining bottlenecks in Python code performance. I used it to profile the program when she was looking for a spelling for the 23-letter word. Here is a compressed version of the report:
Line # % Time Line Contents =============================== 30 @profile 31 def spell(word, symbols=ELEMENTS): 32 71.0 groupings = generate_groupings(len(word)) 33 34 15.2 spellings = [map_word(word, grouping) for grouping in groupings] 35 36 elemental_spellings = [ 37 0.0 tuple(token.capitalize() for token in spelling) 38 13.8 for spelling in spellings 39 if set(s.lower() for s in spelling) <= set(s.lower() for s in symbols) 40 ] 41 42 0.0 return elemental_spellings Line # % Time Line Contents =============================== 45 @profile 46 def generate_groupings(word_length, glyhp_sizes=(1, 2)): 47 cartesian_products = ( 48 0.0 product(glyph_sizes, repeat=r) 49 0.0 for r in range(1, word_length + 1) 50 ) 51 52 0.0 groupings = tuple( 53 0.0 grouping 54 100.0 for grouping in chain.from_iterable(cartesian_products) 55 if sum(grouping) == word_length 56 ) 57 58 0.0 return groupings It's no wonder that generate_groupings() works so long. The problem that she is trying to solve is a special case of the sum of subsets problem , which is an NP-complete problem . Finding a Cartesian product quickly becomes expensive, and generate_groupings() searches for numerous Cartesian products.
You can perform an asymptotic analysis to see how bad everything is:
- We assume that
glyph_sizesalways contain two elements (1 and 2). product()findsrtimes the Cartesian product of a set of two elements, so the time complexity forproduct()isO(2^r).product()is called in a loop that repeatsword_lengthtimes, so if we equatentoword_length, the time complexity for the entire cycle will beO(2^r * n).- But
rgets different values for each run of the loop, so in fact the time complexity is closer toO(2^1 + 2^2 + 2^3 + ... + 2^(n-1) + 2^n). - And since
2^0 + 2^1 + ... + 2^n = 2^(n+1) - 1, the resulting time complexity isO(2^(n+1) - 1), orO(2^n).
With O(2^n) it can be expected that the execution time will double with each word_length increment. Awful
I have been thinking about the performance problem for many weeks. It was necessary to solve two interrelated, but different tasks:
- Processing a list of words of different lengths.
- Handling a single, but very long word.
The second task turned out to be much more important, because it influenced the first one. Although I did not immediately figure out how to improve the processing in the second case, but I had ideas about the first, so I started with it.
Task 1: to be lazy
Laziness is a virtue not only for programmers , but also for the programs themselves. The solution of the first problem required the addition of laziness. If the program will check a long list of words, then how to make it do as little work as possible?
Check for incorrect characters
Naturally, I thought that the list probably contains words containing characters that are not listed in the periodic table. It makes no sense to spend time searching for spellings for such words. So, the list can be processed faster if you quickly find and throw out such words.
Unfortunately, the only characters not represented in the table were j and q.
>>> set('abcdefghijklmnopqrstuvwxyz') - set(''.join(ELEMENTS).lower()) ('j', 'q') And in my dictionary only 3% of words contained these letters:
>>> with open('/usr/share/dict/american-english', 'r') as f: ... words = f.readlines() ... >>> total = len(words) >>> invalid_char_words = len( ... [w for w in words if 'j' in w.lower() or 'q' in w.lower()] ... ) ... >>> invalid_char_words / total * 100 3.3762962340988287 Throwing them out, I got a performance boost of only 2%:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english [...] real 15m44.246s user 15m17.557s sys 0m22.980s It was not the improvement I was hoping for, so I moved on to the next idea.
Memoization
Memoisation is a technique for storing the output of a function and returning it if the function is called again with the same input data. Memotized functions need to generate output data only once based on specific inputs. This is very useful when using expensive functions that are repeatedly called with the same multiple inputs. But memoization works only for pure functions.
generate_groupings() was the perfect candidate. It is unlikely to encounter a very large range of input data and is very expensive to perform when processing long words. The functools package facilitates memoization by providing the decorator @lru_cache() .
The generate_groupings() memoization has led to a decrease in execution time — noticeably, although not enough:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english [...] real 11m15.483s user 10m54.553s sys 0m17.083s But still not bad for the only decorator from the standard library!
Task 2: be smart
My optimizations helped a little with the first task, but the key unsolved problem remained the inefficiency of generate_groupings() , large individual words were still processed for a very long time:
$ time ./stoichiograph.py nonrepresentationalisms [...] real 0m20.275s user 0m20.220s sys 0m0.037s Laziness can lead to some progress, but sometimes you need to be smart.
Recursion and DAG
Dozing off one evening, I experienced a flash of inspiration and ran to the marker board to draw it:

I thought that I could take any string, pull out all the one and two-character notations, and then in both cases recurs the rest. After going through the whole line, I will find all the designations of the elements and, most importantly, I will receive information about their structure and order. I also thought that the graph could be an excellent option for storing such information.
If a series of recursive function calls for the perfect word amputation looks like this:
'a' 'mputation' 'm' 'putation' 'p' 'utation' 'u' 'tation' 't' 'ation' 'a' 'tion' 't' 'ion' 'i' 'on' 'o' 'n' 'n' '' 'on' '' 'io' 'n' 'ti' 'on' 'at' 'ion' 'ta' 'tion' 'ut' 'ation' 'pu' 'tation' 'mp' 'utation' 'am' 'putation' then after filtering all the symbols that do not satisfy the periodic table, you can get a similar graph:
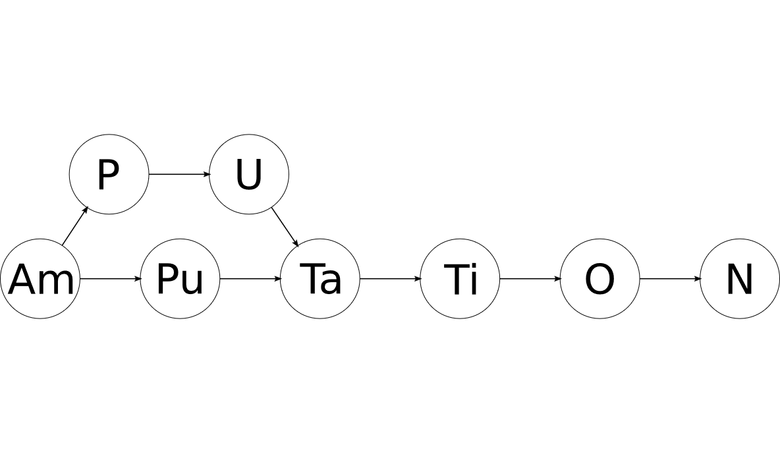
The result is a directed acyclic graph (DAG), each node of which contains the designation of a chemical element. All paths from the first node to the last will be valid spellings of the source word in the form of chemical elements!
Before that, I did not work with graphs, but I found a very useful essay that describes the basics, including an effective search for all paths between two nodes. In the excellent book 500 Lines or Less there is a chapter with another example of a graph implementation in Python. These examples I took as a basis.
Having implemented and tested a simple graph class, I turned my drawing on the board into a function:
# . . Node = namedtuple('Node', ['value', 'position']) def build_spelling_graph(word, graph, symbols=ELEMENTS): """ , - . , . """ def pop_root(remaining, position=0, previous_root=None): if remaining == '': graph.add_edge(previous_root, None) return single_root = Node(remaining[0], position) if single_root.value.capitalize() in symbols: graph.add_edge(previous_root, single_root) if remaining not in processed: pop_root( remaining[1:], position + 1, previous_root=single_root ) if len(remaining) >= 2: double_root = Node(remaining[0:2], position) if double_root.value.capitalize() in symbols: graph.add_edge(previous_root, double_root) if remaining not in processed: pop_root( remaining[2:], position + 2, previous_root=double_root ) processed.add(remaining) processed = set() pop_root(word) Win
While the head-on algorithm ran awfully long ( O(2^n) ), the recursive lasted O(n) . Much better! When I for the first time ran a svezheoptimizirovannuyu program on his dictionary, I was shocked:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english [...] real 0m11.299s user 0m11.020s sys 0m0.17ys Instead of 16 minutes, I got 10 seconds, instead of 120 words per second - 10,800 words!
For the first time, I really appreciated the power and value of data structures and algorithms.
Longest word
With the new features I was able to find the longest word, broken down into chemical elements: floccinaucinihilipilificatiousness. It is a derivative of floccinaucinihilipilification , which means an action or habit of describing something or treating something as unimportant, valueless or useless. This word is often called the longest non-technical word in the English language.
Floccinaucinihilipilificatiousness can be represented in the form of 54 spellings, all of them are encrypted in this beautiful graph:
Well spent time
Someone may say that all of the above is complete nonsense, but for me it has become a valuable and important experience. When I started my project, I was relatively inexperienced in programming and had no idea where to start. It moved slowly, and it took quite a while until I achieved a satisfactory result (see the history of commits , there are big breaks when I switched to other projects).
Nevertheless, I learned a lot and learned a lot. It:
- Combinatorics
- Performance profiling
- Time complexity
- Memoization
- Recursion
- Graphs and trees
The understanding of these concepts helped me many times. Especially important for my simulation project on n-bodies recursion and trees.
Finally, it was nice to find the answer to my own original question. I know that you no longer need to think about splitting into chemical elements, because I now have a tool for this that you can get and you can use pip install stoichiograph .
Discussion
Kind people (and several well-intentioned bots) participated in the discussion of this article in the r / programming branch.
Additional materials
I got a lot of inspiration from the elegant solutions to some interesting problems, the solutions belong to Peter Norvig:
Two informative articles about performance profiling in Python:
')
Source: https://habr.com/ru/post/328986/
All Articles
