The evolution of fractal monsters
Today we will draw geometric fractals, which are paid undeservedly little attention. Meanwhile, here each fractal is a small masterpiece that amazes the imagination!

Then a lot of pictures and gif-animation. But before you go under the cut, look at the picture above and tell me what is drawn on it?
Consider one curious algorithm on the example of a famous fractal - the Levy curve.
We have two points A1 and A2. Find a point A3, for which angle A1 = 45 °, and angle A3 = 90 °.
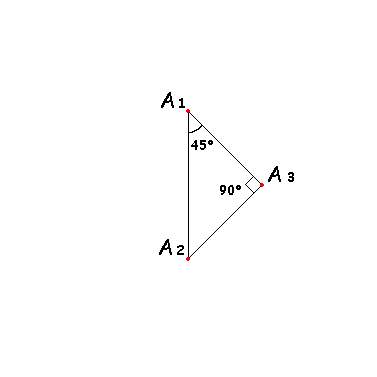
Perform the same operation for points A1, A3 and A3, A2.
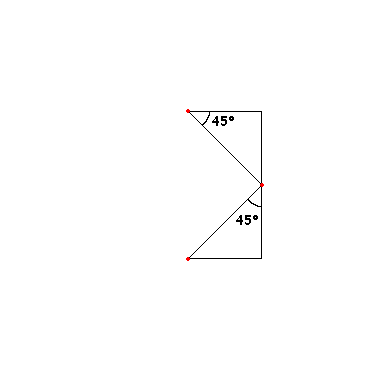
And then recursively for each pair of points.
Third iteration:

At 14 iterations, this curve looks like this:

More visually on javascript:
')
→ Launch in browser
By slightly modifying the above code, we can draw another known fractal curve - the Dragon Harter-Heituey. To do this, starting from the second iteration, we alternate the angles of 45 ° and -45 °
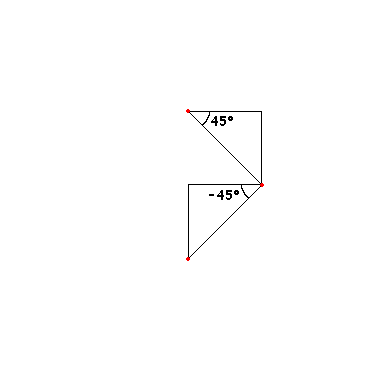
Third iteration:

At 14 iterations, this curve looks like this:
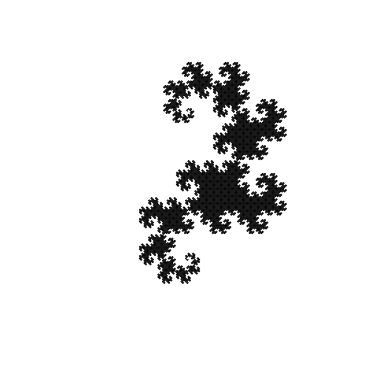
→ Launch in browser
We have changed our function just a little by adding another angle to it, and the fractal has changed beyond recognition! In dynamics (change the second angle in increments of 5 °):
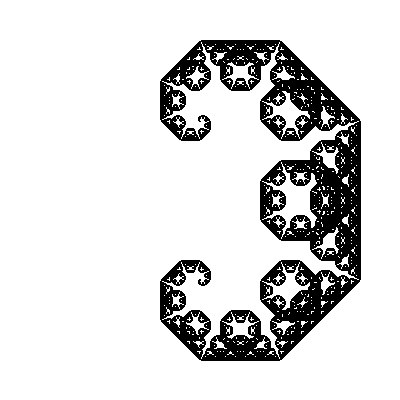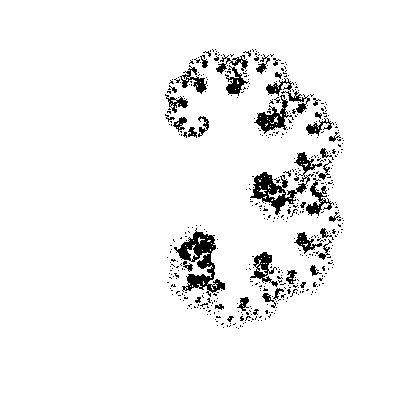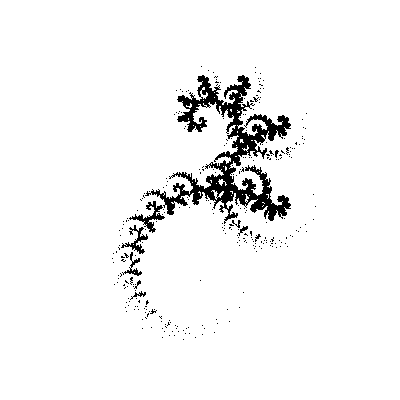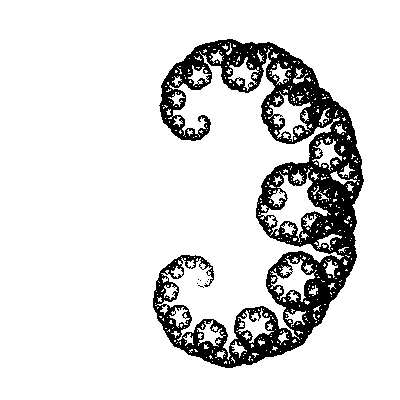
And here our inquiring mind starts asking questions. But what if you try to use other angles instead of [45, -45] ? Let's say [30, -60] . Or [30, -30, -60, 60] . Rewrite our function so that it takes an array with corners as one of the arguments.
Run in the browser (Separate the values of the angles in degrees, press “draw!”)
From this point on, we will draw only points, not connecting them with lines ... purely for aesthetic reasons. Fractal [30, -30, -60, 60] drawn by lines and dots:

Special attention should be paid to the fact that all points A3 lie on a circle with a diameter of A1A2:

If the points are inside (or outside) the circle - the fractal turns out to be too compressed (or vice versa - it goes beyond the drawing area). Clearly:

With this cosine we align the points along the circumference:
It is not difficult to see that using an angle of 120 ° we get the same point as with an angle of -60 °. Therefore, all angles are in the range (-90 °, 90 °).
Let's try to enter into our script different combinations of angles.
Several random fractals with angles of -45 ° / 45 ° (clickable):





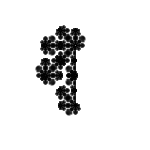







With angles of -30 ° / 30 ° / -60 ° / 60 °:











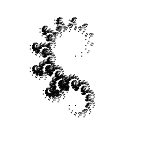













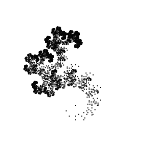


With angles of -15 ° / 15 ° / -30 ° / 30 ° / -45 ° / 45 ° / -60 ° / 60 ° / -75 / 75 °:

























... So you can continue for a very long time. If we use angles of 15 ° / 30 ° / 45 ° / 60 ° / 75 ° (positive and negative) and, say, draw "octagonal" fractals - how many total fractals can we draw? Approximately 10 ^ 8 = 100 000 000 pieces. In addition, the set of "octagonal" fractals does not intersect with a set of, say, "nine-corner" fractals (with the exception of fractals, in which all angles are the same). In general, a lot of fractals can be drawn with this algorithm.
Manually searching for something among this set, without knowing how this “something” should look like, is a bit difficult. What prevents us from screwing the genetic algorithm here? Nothing. Screw!
Genetic algorithm - a heuristic search algorithm that uses the mechanisms of biological evolution. The algorithm is simple, intuitive and at the same time quite effective.
It is divided into several stages.
Each stage is more visual on javascript.
Initial population
The randomangl function is called with three arguments: the minimum angle, the maximum angle, and the pitch. Conveniently, if we want to fill the initial population with certain angles. For example, you can call a function with the following arguments:
randomangl (-45, 45, 90) - generates angles of -45 ° / 45 °
randomangl (-60, 60, 30) - generates angles of -60 ° / -30 ° / 30 ° / 60 °
randomangl (-75, 75, 15) - generates angles of -75 ° / -60 ° / -45 ° / -30 ° / -15 ° / 15 ° / 30 ° / 45 ° / 60 ° / 75 °
Angles 0 ° do not use. The fractal [45 °, 0 °] would look like this:

We get the same fractal [45 °] , only in the place where we are trying to draw 0 ° - the points merge (all further recursion in this place becomes meaningless). For the same reason, it makes no sense to generate fractals using 90 °. For the initial population, it is best to call the randomangl function (-75, 75, 15) . For mutations, randomangl (-89, 89, 1) .
Create several populations with different numbers of angles ( anglemin , anglemax ). We initialize a separate array with fitness coefficients. The first gene in each individual is forcibly made positive - fractals [45 °, -45 °] and [-45 °, 45 °] are symmetrical.
Selection
In general, the fitness of each individual, in classical genetic algorithms, is determined by a special fitness-function. The function evaluates how each of the individuals solves the problem. In our case, it is not possible to clearly formulate the task (we don’t know how this “something” should look like), therefore we will tie in the quality of the fitness function to the user's algorithm.
There are two options. It would be possible to draw all the fractals from the populations and suggest the user to select the best ones, but there may be some difficulties - how to choose the best fractals when they all look impressive? It is much easier to compare two random fractals.
Interface:

There are two canvases on the page: myCanvas1 and myCanvas2. And two buttons: onclick = "selecter (1);" and onclick = "selecter (2);"
Call the function that draws two random fractals:
In the function get2fractals, select a random population.
In the drawcanvas function , check if (n == 1) - in order not to draw two identical fractals. The population number and the number of two fractals are stored in global variables ( PopulationNumber and FractalNumber [] ).
When the user presses the Select button next to the fractal he likes, we call the following function:
Which increases the coefficient of fitness for the selected fractal and draws two new fractals.
We assume that the user was bona fide and made the election no less than the number of individuals in the population, before starting the mechanism of evolution.
Crossbreeding and mutations
We take in turn each population. We write all the individuals in a temporary array, there we write their fitness coefficients. Sort the temporary array by these coefficients. Cut off the half (the fittest). The old two arrays are reset so that there is nothing extra left. We pull from a temporary array of two ancestors, form two descendants. We fill the population with ancestors and descendants.
We make mutations. A small note. Instead of the percentage of mutations in the entire population, we use the probability of mutation of a single individual.
Exchange option available. With this option, a model of migration of individuals between populations is implemented.
If the Exchanges checkbox is checked, alternately for each population, one random individual with a probability of 50% can exchange genes with a random individual from the next population (population n + 1). The genes in the genotypes of the next population are larger, the exchange is as follows. We select a random gene in an individual in the population n + 1, insert it in the same position in the genotype of the individual in population n. Swap individuals:

It remains to add a whistle (css buttons, saving the entire process to localStorage, displaying Parents Tree ...).
Sources can be viewed on GitHub
Or run in the browser by going to the project site (carefully, you can stick!)
The result of my selection is in the picture at the beginning of the publication.
So in conclusion I’ll add that 2D is good, and 3D is even better!

You can twist a fractal with a mouse in three dimensions here . Through a slash we drive in pairs of angles / alpha / beta / alpa / beta / ... into the address bar.

Alpha - is already familiar to us the angle of rotation. New angle Beta - turning point A3 around axis A1A2.

Then a lot of pictures and gif-animation. But before you go under the cut, look at the picture above and tell me what is drawn on it?
Algorithm
Consider one curious algorithm on the example of a famous fractal - the Levy curve.
We have two points A1 and A2. Find a point A3, for which angle A1 = 45 °, and angle A3 = 90 °.

Perform the same operation for points A1, A3 and A3, A2.

And then recursively for each pair of points.
Third iteration:

At 14 iterations, this curve looks like this:

More visually on javascript:
')
JS source
<canvas id="myCanvas"></canvas> <script> window.onload=function(){ var canvas=document.getElementById('myCanvas'); var context=canvas.getContext('2d'); canvas.width=800, canvas.height=800; context.beginPath(); recurs(context, 17, 400, 250, 400, 550); // , context.stroke(); }; var angle=45*Math.PI/180; // function recurs(context, n, x0, y0, x1, y1){ //n , A1(x0,y0) A2(x1,y1) if (n==0){ context.moveTo(x0,y0); context.lineTo(x1,y1); }else{ var xx=Math.cos(angle)*((x1-x0)*Math.cos(angle)-(y1-y0)*Math.sin(angle))+x0; var yy=Math.cos(angle)*((x1-x0)*Math.sin(angle)+(y1-y0)*Math.cos(angle))+y0; // A3 recurs(context, n-1, x0, y0, xx, yy); //A1, A3 recurs(context, n-1, xx, yy, x1, y1); //A3, A2 } } </script> → Launch in browser
By slightly modifying the above code, we can draw another known fractal curve - the Dragon Harter-Heituey. To do this, starting from the second iteration, we alternate the angles of 45 ° and -45 °

Third iteration:

At 14 iterations, this curve looks like this:
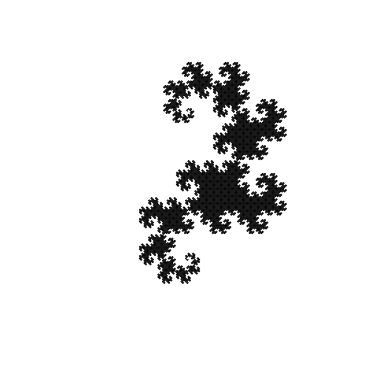
Modified source fragment
}else{ angle2=angle*k; // <- var xx=Math.cos(angle2)*((x1-x0)*Math.cos(angle2)-(y1-y0)*Math.sin(angle2))+x0; var yy=Math.cos(angle2)*((x1-x0)*Math.sin(angle2)+(y1-y0)*Math.cos(angle2))+y0; recurs(context, n-1, x0, y0, xx, yy, 1); // - k recurs(context, n-1, xx, yy, x1, y1, -1); } → Launch in browser
We have changed our function just a little by adding another angle to it, and the fractal has changed beyond recognition! In dynamics (change the second angle in increments of 5 °):
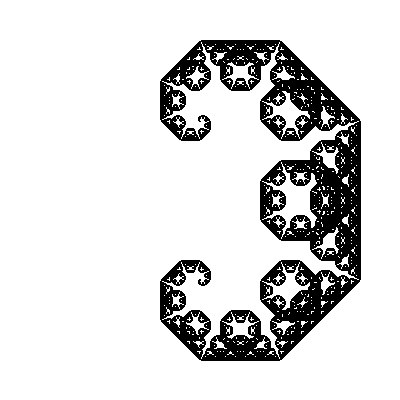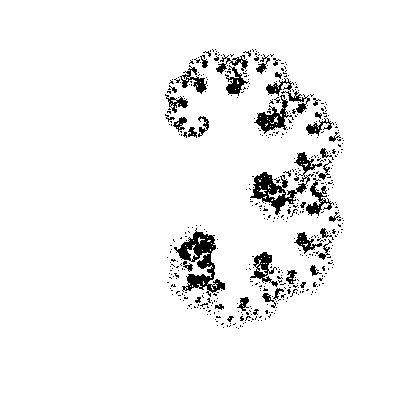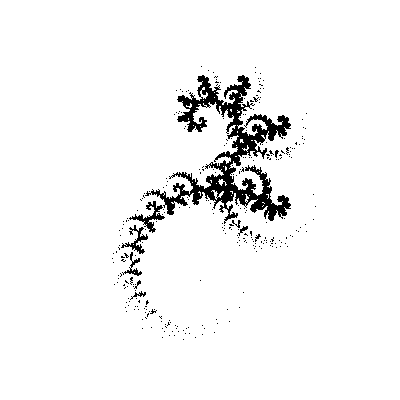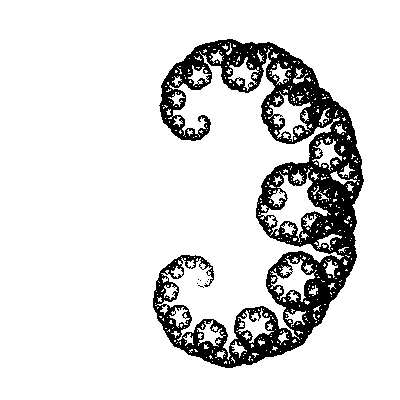
And here our inquiring mind starts asking questions. But what if you try to use other angles instead of [45, -45] ? Let's say [30, -60] . Or [30, -30, -60, 60] . Rewrite our function so that it takes an array with corners as one of the arguments.
The final version of the function
The position array stores the angle number from the arr array for the current recursion depth (n).
function recurs(context, arr, position, n, x0, y0, x1, y1){ if (n==0){ context.fillRect(x1,y1, 1,1); return position; }else{ if (!position[n]) position[n]=0; var xx=Math.cos(arr[position[n]])*((x1-x0)*Math.cos(arr[position[n]])-(y1-y0)*Math.sin(arr[position[n]]))+x0; var yy=Math.cos(arr[position[n]])*((x1-x0)*Math.sin(arr[position[n]])+(y1-y0)*Math.cos(arr[position[n]]))+y0; position[n]++; if (position[n]==arr.length) position[n]=0; position=recurs(context, arr, position, n-1, x0, y0, xx, yy); position=recurs(context, arr, position, n-1, xx, yy, x1, y1); return position; } } The position array stores the angle number from the arr array for the current recursion depth (n).
Run in the browser (Separate the values of the angles in degrees, press “draw!”)
From this point on, we will draw only points, not connecting them with lines ... purely for aesthetic reasons. Fractal [30, -30, -60, 60] drawn by lines and dots:

Special attention should be paid to the fact that all points A3 lie on a circle with a diameter of A1A2:

If the points are inside (or outside) the circle - the fractal turns out to be too compressed (or vice versa - it goes beyond the drawing area). Clearly:

With this cosine we align the points along the circumference:
var xx=Math.cos(arr[position[n]])* ... var yy=Math.cos(arr[position[n]])* ... It is not difficult to see that using an angle of 120 ° we get the same point as with an angle of -60 °. Therefore, all angles are in the range (-90 °, 90 °).
Let's try to enter into our script different combinations of angles.
"Little masterpieces"
Several random fractals with angles of -45 ° / 45 ° (clickable):





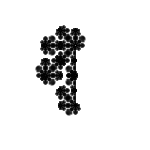







With angles of -30 ° / 30 ° / -60 ° / 60 °:











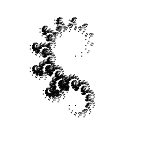
















With angles of -15 ° / 15 ° / -30 ° / 30 ° / -45 ° / 45 ° / -60 ° / 60 ° / -75 / 75 °:

























... So you can continue for a very long time. If we use angles of 15 ° / 30 ° / 45 ° / 60 ° / 75 ° (positive and negative) and, say, draw "octagonal" fractals - how many total fractals can we draw? Approximately 10 ^ 8 = 100 000 000 pieces. In addition, the set of "octagonal" fractals does not intersect with a set of, say, "nine-corner" fractals (with the exception of fractals, in which all angles are the same). In general, a lot of fractals can be drawn with this algorithm.
Manually searching for something among this set, without knowing how this “something” should look like, is a bit difficult. What prevents us from screwing the genetic algorithm here? Nothing. Screw!
Evolution
Genetic algorithm - a heuristic search algorithm that uses the mechanisms of biological evolution. The algorithm is simple, intuitive and at the same time quite effective.
It is divided into several stages.
- An initial population is created, consisting of a small number of individuals. Each individual is an array of fixed length with a set of genes (genotype). Genotypes of the initial population are filled randomly. In relation to our problem, genes are the angles with which we will draw fractals.
- At the next stage, selection takes place. For each individual we consider the coefficient of fitness ( fitness ). The better the individual, the higher the coefficient. Sort the population by this coefficient. We divide the population in half - from the fittest we will form the next population. (How to share and what to choose for the next population is a topic that you can argue about for a long time).
- The next stage is crossing. From the fittest we choose (randomly) two individuals - parents. We make two descendants: we randomly take part of the genes of one parent and part of the genes of the other, fill them with the genotype of one of the descendants. The remaining genes go to the second descendant. Take the next two parents. Perform the same operation. So until the parents run out. From parents and descendants form a new population.
- The final stage - mutations. We take a certain percentage of individuals from the new population, for each of them (individuals), we randomly select a gene and replace it with a random value. Thus, we add genes to our gene pool that were not in the initial population and which, in the long term, can form the best results. In addition, by increasing the percentage of mutations, one can to some extent solve the problem of convergence to a local optimum.
Each stage is more visual on javascript.
Initial population
Generate corners
function randomangl(min, max, step){ if(step==0) step=1; var rand=Math.floor(Math.random() * (max/step - min/step + 1)) + min/step; if(rand==0) rand=1; rand*=step; if(rand>max) rand=max; return Math.round(rand); } The randomangl function is called with three arguments: the minimum angle, the maximum angle, and the pitch. Conveniently, if we want to fill the initial population with certain angles. For example, you can call a function with the following arguments:
randomangl (-45, 45, 90) - generates angles of -45 ° / 45 °
randomangl (-60, 60, 30) - generates angles of -60 ° / -30 ° / 30 ° / 60 °
randomangl (-75, 75, 15) - generates angles of -75 ° / -60 ° / -45 ° / -30 ° / -15 ° / 15 ° / 30 ° / 45 ° / 60 ° / 75 °
Angles 0 ° do not use. The fractal [45 °, 0 °] would look like this:

We get the same fractal [45 °] , only in the place where we are trying to draw 0 ° - the points merge (all further recursion in this place becomes meaningless). For the same reason, it makes no sense to generate fractals using 90 °. For the initial population, it is best to call the randomangl function (-75, 75, 15) . For mutations, randomangl (-89, 89, 1) .
Create the initial population
population=[]; fitness=[]; for(var n=anglemin; n<=anglemax; n++){ population[n]=[]; fitness[n]=[]; for(var i=0; i<PopulationSize; i++){ population[n][i]=[]; fitness[n][i]=0; for(var j=0; j<n; j++){ population[n][i][j]=randomangl(min, max, step); if(j==0) population[n][i][j]=Math.abs(population[n][i][j]); } } } Create several populations with different numbers of angles ( anglemin , anglemax ). We initialize a separate array with fitness coefficients. The first gene in each individual is forcibly made positive - fractals [45 °, -45 °] and [-45 °, 45 °] are symmetrical.
Selection
In general, the fitness of each individual, in classical genetic algorithms, is determined by a special fitness-function. The function evaluates how each of the individuals solves the problem. In our case, it is not possible to clearly formulate the task (we don’t know how this “something” should look like), therefore we will tie in the quality of the fitness function to the user's algorithm.
There are two options. It would be possible to draw all the fractals from the populations and suggest the user to select the best ones, but there may be some difficulties - how to choose the best fractals when they all look impressive? It is much easier to compare two random fractals.
Interface:

There are two canvases on the page: myCanvas1 and myCanvas2. And two buttons: onclick = "selecter (1);" and onclick = "selecter (2);"
Call the function that draws two random fractals:
Draw two random fractals
function get2fractals(){ PopulationNumber=Math.floor(Math.random() * (anglemax - anglemin + 1))+anglemin; drawcanvas(1); drawcanvas(2); } function drawcanvas(n){ var canvas=document.getElementById('myCanvas'+n); var context=canvas.getContext('2d'); canvas.width=canvasSize, canvas.height=canvasSize; context.fillStyle = 'rgb(255,255,255)'; context.fillRect (0, 0, canvas.width, canvas.height); var position=[]; if(n==1){ FractalNumber[1]=Math.floor(Math.random() * (PopulationSize)); }else{ do{ var rnd = Math.floor(Math.random() * (PopulationSize)); }while(rnd==FractalNumber[1]) FractalNumber[2]=rnd; } var array1fractal=population[PopulationNumber][FractalNumber[n]]; context.fillStyle = 'rgb(0,0,0)'; draw(context, array1fractal, position, iteration, xA, yA, xB, yB); } In the function get2fractals, select a random population.
In the drawcanvas function , check if (n == 1) - in order not to draw two identical fractals. The population number and the number of two fractals are stored in global variables ( PopulationNumber and FractalNumber [] ).
When the user presses the Select button next to the fractal he likes, we call the following function:
Select
function selecter(n){ fitness[PopulationNumber][FractalNumber[n]]++; get2fractals(); } Which increases the coefficient of fitness for the selected fractal and draws two new fractals.
We assume that the user was bona fide and made the election no less than the number of individuals in the population, before starting the mechanism of evolution.
Crossbreeding and mutations
Crosses and mutations
function sortf(a, b) { if (a[1] < b[1]) return 1; else if (a[1] > b[1]) return -1; else return 0; } function evolution(){ var mutation=document.getElementById("mutatepercent").value; var exchange=document.getElementById("exchangepercent").checked; var sizehalf=PopulationSize/2; var sizequarter=sizehalf/2; for(var n=anglemin; n<=anglemax; n++){ var arrayt=[]; for(var i=0; i<PopulationSize; i++){ arrayt[i]=[]; arrayt[i][0]=population[n][i]; arrayt[i][1]=fitness[n][i]; } arrayt.sort(sortf); arrayt.length=sizehalf; population[n].length=0; fitness[n].length=0; for(var i=0; i<sizequarter; i++){ var i0=i*4; var i1=i*4+1; var i2=i*4+2; var i3=i*4+3; var removed1=Math.floor(Math.random()*(arrayt.length)); var parent1f = arrayt.splice(removed1,1); var parent1=parent1f[0][0]; var removed2=Math.floor(Math.random()*(arrayt.length)); var parent2f = arrayt.splice(removed2,1); var parent2=parent2f[0][0]; var child1=[]; var child2=[]; for(var j=0; j<n; j++){ var gen=Math.round(Math.random()); if(gen==1){ child1[j]=parent1[j]; child2[j]=parent2[j]; }else{ child1[j]=parent2[j]; child2[j]=parent1[j]; } } population[n][i0]=parent1; population[n][i1]=parent2; population[n][i2]=child1; population[n][i3]=child2; fitness[n][i0]=0; fitness[n][i1]=0; fitness[n][i2]=0; fitness[n][i3]=0; } if(mutation>0){ var m=100/mutation; for(var i=0; i<PopulationSize; i++){ var rnd=Math.floor(Math.random()*(m))+1; if(rnd==1){ var mutatedgene=Math.floor(Math.random()*(n)); population[n][i][mutatedgene]=randomangl(minm, maxm, stepm); } } } } if(exchange){ ///... } get2fractals(); } We take in turn each population. We write all the individuals in a temporary array, there we write their fitness coefficients. Sort the temporary array by these coefficients. Cut off the half (the fittest). The old two arrays are reset so that there is nothing extra left. We pull from a temporary array of two ancestors, form two descendants. We fill the population with ancestors and descendants.
We make mutations. A small note. Instead of the percentage of mutations in the entire population, we use the probability of mutation of a single individual.
Exchange option available. With this option, a model of migration of individuals between populations is implemented.
Migration Model
if(exchange){ var n=anglemin; while(n<population.length){ var rnd=Math.round(Math.random()); var np=n+1; if(rnd==1 && (typeof population[np]!="undefined")){ var i1=Math.floor(Math.random() * (PopulationSize)); var i2=Math.floor(Math.random() * (PopulationSize)); var tempa1=population[np][i1]; var tempa2=population[n][i2]; var indexofexcessgene=Math.floor(Math.random()*(tempa1.length)); var excessgene=tempa1.splice(indexofexcessgene,1); tempa2.splice(indexofexcessgene,0,excessgene[0]); population[np][i1]=tempa2; population[n][i2]=tempa1; n+=2; }else{ n++; } } } If the Exchanges checkbox is checked, alternately for each population, one random individual with a probability of 50% can exchange genes with a random individual from the next population (population n + 1). The genes in the genotypes of the next population are larger, the exchange is as follows. We select a random gene in an individual in the population n + 1, insert it in the same position in the genotype of the individual in population n. Swap individuals:

It remains to add a whistle (css buttons, saving the entire process to localStorage, displaying Parents Tree ...).
Sources can be viewed on GitHub
Or run in the browser by going to the project site (carefully, you can stick!)
The result of my selection is in the picture at the beginning of the publication.
So in conclusion I’ll add that 2D is good, and 3D is even better!

You can twist a fractal with a mouse in three dimensions here . Through a slash we drive in pairs of angles / alpha / beta / alpa / beta / ... into the address bar.

Alpha - is already familiar to us the angle of rotation. New angle Beta - turning point A3 around axis A1A2.
bug in 3D algorithm
In the 3D algorithm there is a funny bug (feature) that did not fix it. To draw the Dragon Harter-Heytuey, you need to use 4 pairs of angles: 45/180/45/0/45/0/45/180 .
3D algorithm can draw two-dimensional fractals, which can not draw a 2D algorithm. For example:
45/0/45/180/45/180/45/180/45/0

45/180/45/180/45/0/45/180/45/180 /

A small gallery of two-dimensional fractals drawn by this algorithm.

3D algorithm can draw two-dimensional fractals, which can not draw a 2D algorithm. For example:
45/0/45/180/45/180/45/180/45/0

45/180/45/180/45/0/45/180/45/180 /

A small gallery of two-dimensional fractals drawn by this algorithm.

Source: https://habr.com/ru/post/328568/
All Articles