On the appearance of spirals in a cyclic cellular automaton
About cyclic cellular automata was written in this article . The purpose of this article is to examine the conditions for the emergence of spirals, also known as demons . The means to achieve the goal is to change the initial conditions and monitor the development of the cellular automaton. As a result, general conclusions will be made about the conditions for the formation of spirals.
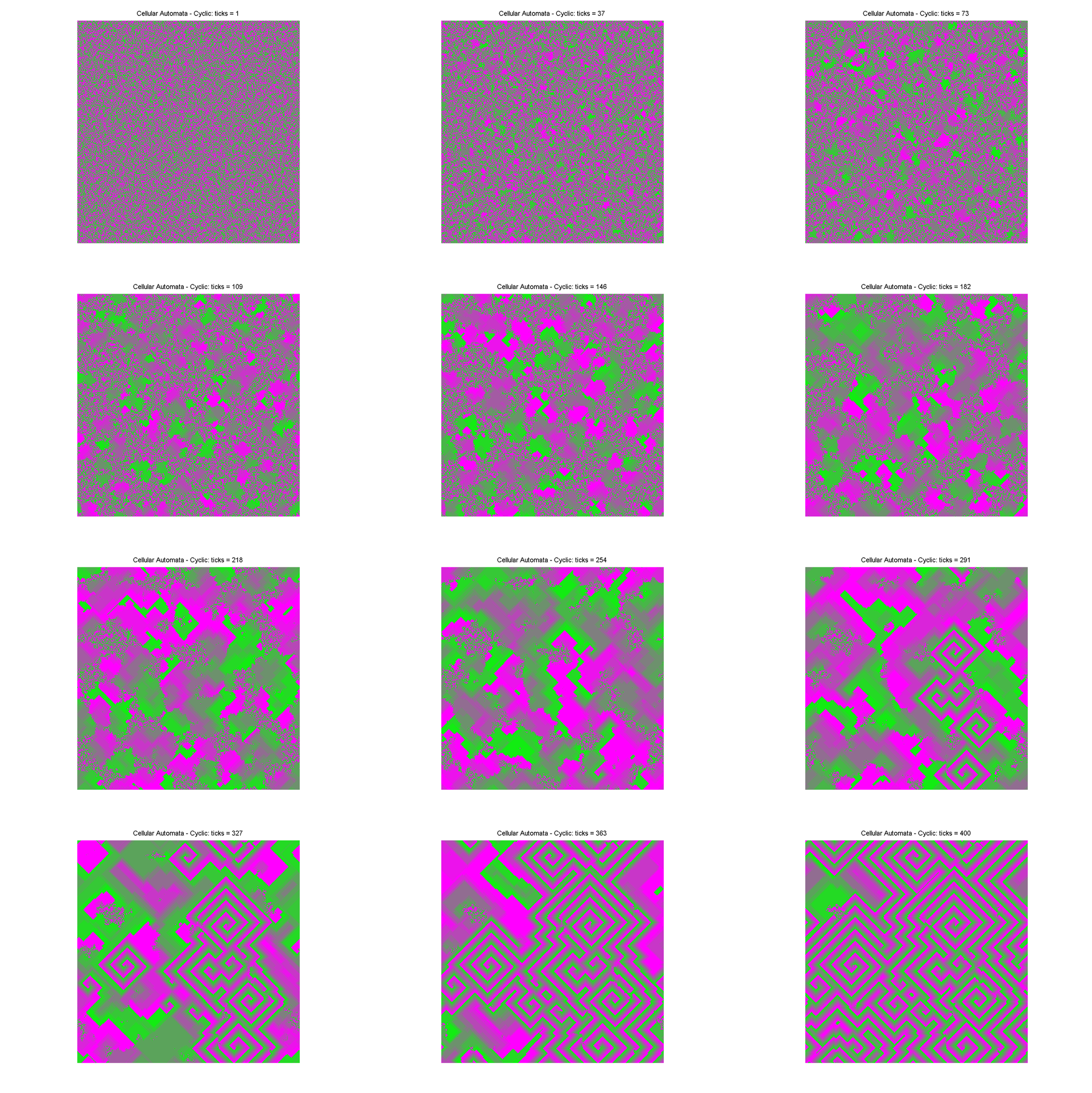
As can be seen from the figure above, the cellular automaton goes through three stages:
1. Random field.
2. Colored areas.
3. Spirals, also known as demons .
Add another dimension to the grid. In this dimension, we will display the state of the cell. The cell will rise until it reaches the top of the cuboid, and then it falls down. Such a model is a good idea of a change in the state of the cellular automaton.
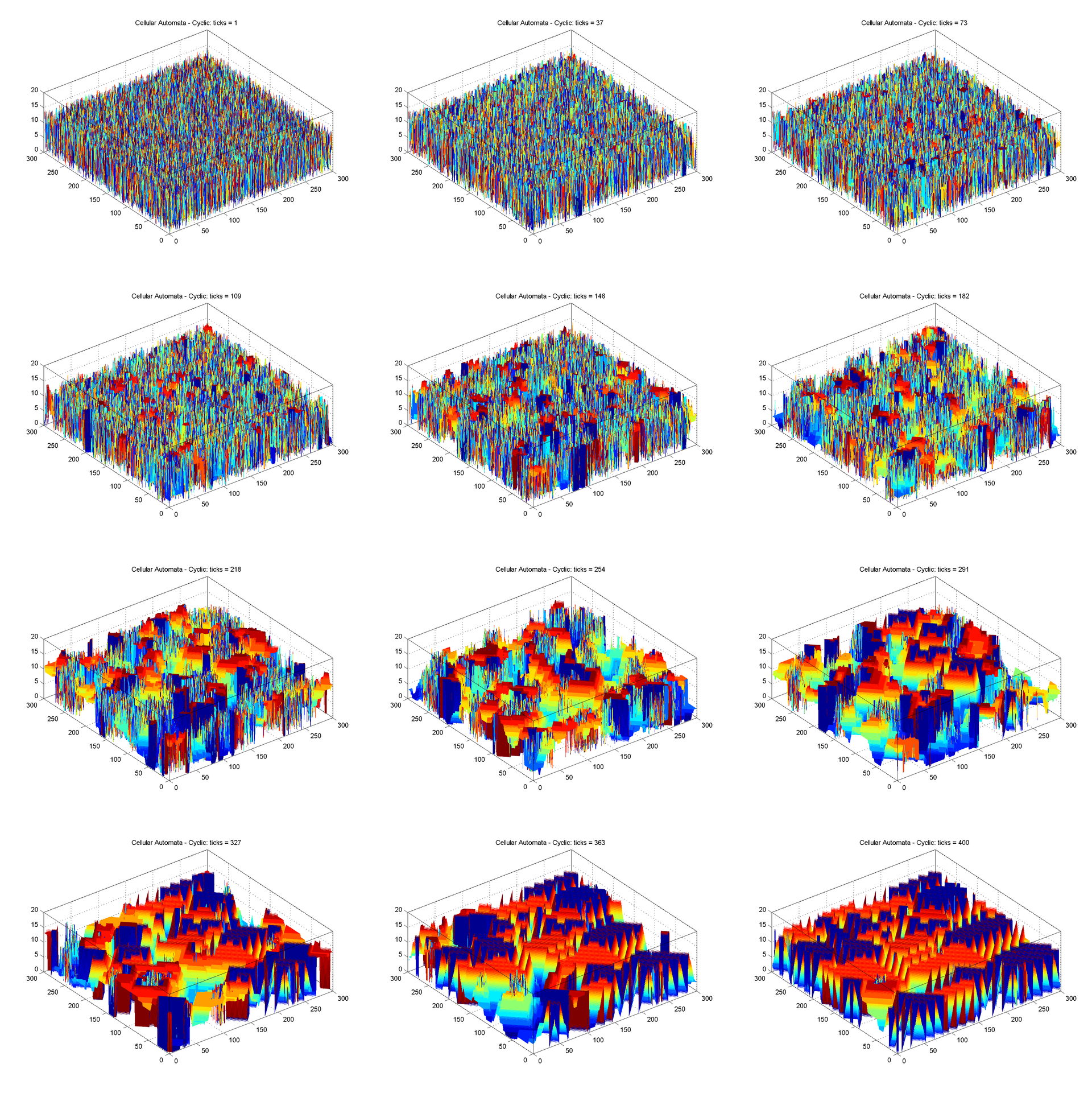
Select several (for example, 12) random cells and consider the change in their states over time.

Now it is not difficult to guess in which of the three stages of the cellular automaton the current cell is at each moment of time:
1. Random field . It is obvious that at the initial moment each cell is in this stage.
2. Color area . As soon as the cell begins to change its state, it enters this stage. The following criterion for this stage can be defined: the number of iterations for which the cell goes through a full cycle is greater than the number of states of the cellular automaton . The considered cellular automaton has 15 states from 0 to 14. If a cell changes state 0 to state 14 in more than 15 iterations of the algorithm (for example, 20 or 25), then it is in the stage Colored area of the cellular automaton.
3. Spirals , also known as demons . If a cell changes state 0 to state 14 in exactly 15 iterations, then it is in the helix stage of a cellular automaton. Thus, the criterion can be: the number of iterations for which the cell goes through a full cycle, exactly equal to the number of states of the cellular automaton .
We draw attention to some features of the transition from one state to another.
1. According to the rules of the cellular automaton, a cell can never return to a lower state unless it is a question of repeating a cycle. For example, from state 9, a cell cannot get to state 8. But from state 14, a cell always falls into state 0, since state 0 is the next state for state 14.
2. According to the rules of the cellular automaton, the cell cannot jump over states.
The presence of boundary states (0 and 14) is a necessary condition for the generation of spirals. However, as will be shown below, the above features of the transition from one state to another impose restrictions on the spatial arrangement of cells in different states, including the boundary.
The figure below shows the change in the proportion of each state during the iterations of the algorithm.

As we can see, changes in fractions are oscillatory. These fluctuations seem erratic and too complex for analysis. However, we try to understand them. To do this, we change the initial conditions of the cellular automaton.

According to the rules of the cellular automaton, a cell in any state cannot arise by itself (except for the zero iteration). To create it, in the neighborhood of the cell there must be a cell with the same state. Thus, if all possible states of the cellular automaton are not initially specified, the missing states will never occur. The cycle will never be closed, and the spiral will never arise.
An important role is played by the spatial arrangement of cells with different states. Consider this by example. 15 cells with all possible states of the cellular automaton are randomly placed on the grid. The remaining cells are initialized to zero state. Thus, we have different distances between the source cells. Run the simulation and see how the fractions of the cells change.

Consider changing fractions in 3D mode.

As can be seen in the figure above, the proportion of cells in state 0 decreases. Because, according to the rules of the cellular automaton, they serve as food for cells with state 1. The fraction of cells in state 1 first increases and then decreases. Cells with state 1 form a colored area. This colored area grows as long as there is only food next to it (cells with a zero state). The colored area itself becomes food and begins to decrease as soon as a successor appears in its area (cell with state 2). The time of growth (the number of iterations) of this colored region depends on the distance between the source cells with state 1 and 2, which is random.
As can be seen from the figure, the fraction of cells in the state above the third is zero. This is due to the fact that the distance between the source cells is too large. At the same time, the number of iterations is limited and equal to 400. The colored area does not reach the next successor within 400 iterations. Thus, our model moves too slowly. Nevertheless, it allows to understand the principle of growth and reduction of color areas:
1. A colored area grows as long as its borders have food (cells with a lower state).
2. The color area begins to shrink when successors appear in its environment (cells with a higher state).
The process of forming colored areas can be accelerated in two ways:
1. Increasing the number of iterations.
2. Reducing the distance between the source cells.
We use the second method. Place the original cells so that they are located at a distance of 10 cells from each other.

Consider fractions on three-dimensional graphics.

In the figure above, we see the movement of the color areas from state 0 to state 13. The color region does not go into the last state, which is 14, because there is no successor (cells with state 14). Although, we placed the cell with this state on the lattice at the very beginning, but the only cell from state 14 was absorbed by its successor (cell with state 0), while the color region with state 13 did not have time to reach it.

State 14 has disappeared from the cellular automaton forever. It will never appear again.

Thus, the cycle will never be closed, and spirals will never be formed. This is an important feature of cyclic cellular automata. Unsuccessful spatial arrangement of cells cannot generate a loop. How to find a good spatial arrangement of cells. Obviously, they should be located as close as possible to each other so that they can interact as quickly as possible (until their successor devours them).
Place the initial cells one by one.

Consider changing fractions on 3D graphics.

As we can see, cell fractions are evenly distributed between all states. The color area goes through all possible states. The loop ends for each starting cell.

We see the formation of a spiral.

Thus, we can conclude: the spiral is a colored area for which three conditions are fulfilled simultaneously:
1. The size of the color area is only one cell.
2. The colored area has food in its neighborhood (cells with a lower state)
3. The color region has successors in its neighborhood (cells with a higher state)
We briefly describe the cyclic cellular automaton.
The lattice is a closed two-dimensional orthogonal grid of square cells, each of which is in one of 15 possible states, ranging from 0 to 14.
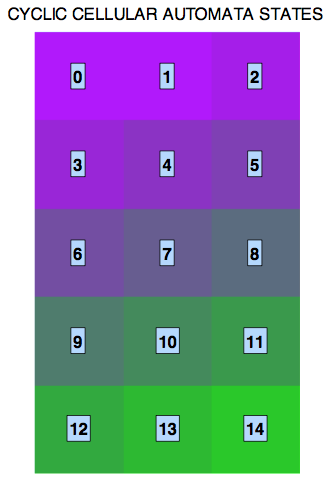
Each cell interacts with its four neighbors — the von Neumann neighborhood. Von Neumann surroundings are cells that are arranged horizontally and vertically. Below is a set of rules for a cyclic cellular automaton.
')

The first generation starts with random states in each of the cells. The next generation is created by applying the above rules simultaneously to each cell of the previous generation. A state change occurs for each cell at the same time. In other words, each generation is a pure function of the previous one. The rules continue to be applied repeatedly, creating new generations.

Each cell interacts with its four neighbors — the von Neumann neighborhood. Von Neumann surroundings are cells that are arranged horizontally and vertically. Below is a set of rules for a cyclic cellular automaton.
')

The first generation starts with random states in each of the cells. The next generation is created by applying the above rules simultaneously to each cell of the previous generation. A state change occurs for each cell at the same time. In other words, each generation is a pure function of the previous one. The rules continue to be applied repeatedly, creating new generations.

As can be seen from the figure above, the cellular automaton goes through three stages:
1. Random field.
2. Colored areas.
3. Spirals, also known as demons .
Add another dimension to the grid. In this dimension, we will display the state of the cell. The cell will rise until it reaches the top of the cuboid, and then it falls down. Such a model is a good idea of a change in the state of the cellular automaton.

Select several (for example, 12) random cells and consider the change in their states over time.

Now it is not difficult to guess in which of the three stages of the cellular automaton the current cell is at each moment of time:
1. Random field . It is obvious that at the initial moment each cell is in this stage.
2. Color area . As soon as the cell begins to change its state, it enters this stage. The following criterion for this stage can be defined: the number of iterations for which the cell goes through a full cycle is greater than the number of states of the cellular automaton . The considered cellular automaton has 15 states from 0 to 14. If a cell changes state 0 to state 14 in more than 15 iterations of the algorithm (for example, 20 or 25), then it is in the stage Colored area of the cellular automaton.
3. Spirals , also known as demons . If a cell changes state 0 to state 14 in exactly 15 iterations, then it is in the helix stage of a cellular automaton. Thus, the criterion can be: the number of iterations for which the cell goes through a full cycle, exactly equal to the number of states of the cellular automaton .
We draw attention to some features of the transition from one state to another.
1. According to the rules of the cellular automaton, a cell can never return to a lower state unless it is a question of repeating a cycle. For example, from state 9, a cell cannot get to state 8. But from state 14, a cell always falls into state 0, since state 0 is the next state for state 14.
2. According to the rules of the cellular automaton, the cell cannot jump over states.
The presence of boundary states (0 and 14) is a necessary condition for the generation of spirals. However, as will be shown below, the above features of the transition from one state to another impose restrictions on the spatial arrangement of cells in different states, including the boundary.
The figure below shows the change in the proportion of each state during the iterations of the algorithm.

As we can see, changes in fractions are oscillatory. These fluctuations seem erratic and too complex for analysis. However, we try to understand them. To do this, we change the initial conditions of the cellular automaton.

According to the rules of the cellular automaton, a cell in any state cannot arise by itself (except for the zero iteration). To create it, in the neighborhood of the cell there must be a cell with the same state. Thus, if all possible states of the cellular automaton are not initially specified, the missing states will never occur. The cycle will never be closed, and the spiral will never arise.
An important role is played by the spatial arrangement of cells with different states. Consider this by example. 15 cells with all possible states of the cellular automaton are randomly placed on the grid. The remaining cells are initialized to zero state. Thus, we have different distances between the source cells. Run the simulation and see how the fractions of the cells change.

Consider changing fractions in 3D mode.

As can be seen in the figure above, the proportion of cells in state 0 decreases. Because, according to the rules of the cellular automaton, they serve as food for cells with state 1. The fraction of cells in state 1 first increases and then decreases. Cells with state 1 form a colored area. This colored area grows as long as there is only food next to it (cells with a zero state). The colored area itself becomes food and begins to decrease as soon as a successor appears in its area (cell with state 2). The time of growth (the number of iterations) of this colored region depends on the distance between the source cells with state 1 and 2, which is random.
As can be seen from the figure, the fraction of cells in the state above the third is zero. This is due to the fact that the distance between the source cells is too large. At the same time, the number of iterations is limited and equal to 400. The colored area does not reach the next successor within 400 iterations. Thus, our model moves too slowly. Nevertheless, it allows to understand the principle of growth and reduction of color areas:
1. A colored area grows as long as its borders have food (cells with a lower state).
2. The color area begins to shrink when successors appear in its environment (cells with a higher state).
The process of forming colored areas can be accelerated in two ways:
1. Increasing the number of iterations.
2. Reducing the distance between the source cells.
We use the second method. Place the original cells so that they are located at a distance of 10 cells from each other.

Consider fractions on three-dimensional graphics.

In the figure above, we see the movement of the color areas from state 0 to state 13. The color region does not go into the last state, which is 14, because there is no successor (cells with state 14). Although, we placed the cell with this state on the lattice at the very beginning, but the only cell from state 14 was absorbed by its successor (cell with state 0), while the color region with state 13 did not have time to reach it.

State 14 has disappeared from the cellular automaton forever. It will never appear again.

Thus, the cycle will never be closed, and spirals will never be formed. This is an important feature of cyclic cellular automata. Unsuccessful spatial arrangement of cells cannot generate a loop. How to find a good spatial arrangement of cells. Obviously, they should be located as close as possible to each other so that they can interact as quickly as possible (until their successor devours them).
Place the initial cells one by one.

Consider changing fractions on 3D graphics.

As we can see, cell fractions are evenly distributed between all states. The color area goes through all possible states. The loop ends for each starting cell.

We see the formation of a spiral.

Thus, we can conclude: the spiral is a colored area for which three conditions are fulfilled simultaneously:
1. The size of the color area is only one cell.
2. The colored area has food in its neighborhood (cells with a lower state)
3. The color region has successors in its neighborhood (cells with a higher state)
Summing up all the observations.
1. If the number of iterations for which a cell goes through a full cycle (changes states from 0 to 14) is more than the number of states of the cellular automaton (15), then this is a colored area .
2. If the number of iterations for which the cell goes through a full cycle is exactly equal to the number of states of the cellular automaton, then this is a spiral .
3. According to the rules of the cellular automaton, a cell in any state cannot arise by itself (except for the zero iteration). To create it, in the neighborhood of the cell there must be a cell with the same state.
4. The color area grows as long as its borders have food (cells with a lower state). The color area begins to shrink when successors appear in its neighborhood (cells with a higher state).
5. An unsuccessful spatial arrangement of source cells may not generate a cycle, because the last few states may disappear forever and never appear again. Thus, the cellular automaton loses several states and is unable to produce more helix.
6. To avoid this, the source cells should be located as close as possible to each other so that they can interact as quickly as possible (until their successors absorb them).
7. The spiral is a colored area for which three conditions are fulfilled simultaneously:
- the size of the color area is only one cell;
- the colored area has food in its neighborhood (cells with a lower state);
- the color area has in its neighborhood successors (cells with a higher state).
2. If the number of iterations for which the cell goes through a full cycle is exactly equal to the number of states of the cellular automaton, then this is a spiral .
3. According to the rules of the cellular automaton, a cell in any state cannot arise by itself (except for the zero iteration). To create it, in the neighborhood of the cell there must be a cell with the same state.
4. The color area grows as long as its borders have food (cells with a lower state). The color area begins to shrink when successors appear in its neighborhood (cells with a higher state).
5. An unsuccessful spatial arrangement of source cells may not generate a cycle, because the last few states may disappear forever and never appear again. Thus, the cellular automaton loses several states and is unable to produce more helix.
6. To avoid this, the source cells should be located as close as possible to each other so that they can interact as quickly as possible (until their successors absorb them).
7. The spiral is a colored area for which three conditions are fulfilled simultaneously:
- the size of the color area is only one cell;
- the colored area has food in its neighborhood (cells with a lower state);
- the color area has in its neighborhood successors (cells with a higher state).
Links
(1) Robert Fisch, David Griffeath, Janko Gravner, CYCLIC CELLULAR AUTOMATA IN TWO DIMENSIONS.
(2) Clifford A. Reiter, Medley of Spirals from Cyclic Cellular Automata.
(3) Yiqing Cai, CYCLIC CELLULAR AUTOMATA ON NETWORKS AND COHOMOLOGICAL WAVES.
(4) Indrajit Banerjee, Prasenjit Chanak, Hafizur Rahaman, CCABC: Cyclic Cellular Automata Based Clustering.
(5) KJ Kwak, YM Baryshnikov, EG Coffman, Cyclic Cellular Automata: A Tool for Self-Organizing Sleep Scheduling in Sensor Networks
(2) Clifford A. Reiter, Medley of Spirals from Cyclic Cellular Automata.
(3) Yiqing Cai, CYCLIC CELLULAR AUTOMATA ON NETWORKS AND COHOMOLOGICAL WAVES.
(4) Indrajit Banerjee, Prasenjit Chanak, Hafizur Rahaman, CCABC: Cyclic Cellular Automata Based Clustering.
(5) KJ Kwak, YM Baryshnikov, EG Coffman, Cyclic Cellular Automata: A Tool for Self-Organizing Sleep Scheduling in Sensor Networks
Source: https://habr.com/ru/post/328314/
All Articles