Corrective (or anti-interference) codes are codes that can detect and, if lucky, correct errors that occurred during data transfer. Even if you have not heard anything about them, you probably met the abbreviation CRC in the list of files in the ZIP-archive or even the inscription ECC on the memory bar. And someone, perhaps, wondered how it turns out that if you scratch a DVD, the data is still read without errors. Of course, if the scratch is not a centimeter thick and did not cut the disc in half.

As you might guess, corrective codes are involved in all this. Actually, the ECC is also decoded - “error-correcting code”, that is, “error correcting code”. A CRC is one of the algorithms that detect errors in the data. He can not fix them, but often it is not required.

Let's see what it is.

To understand the article does not need any special knowledge. It is enough to understand what a vector and a matrix are, how they are multiplied and how to use them to write a system of linear equations.

Attention! Lots of text and little pictures. I tried to explain everything, but without a pencil and paper, the text may seem a bit confusing.

Channels with error

We will first understand where all the errors come from, which we are going to correct. We have the next task. It is necessary to transfer several data blocks, each of which is encoded by a string of binary digits. The resulting sequence of zeros and ones is transmitted through the communication channel. But it so happens that real communication channels are often error prone. Generally speaking, errors can be of different types - there may be an extra figure or some kind of chasm. But we will consider only situations when only replacements of zero by one and vice versa are possible in the channel. And again, for simplicity, we consider such replacements to be equally probable.

Error is an unlikely event (otherwise why do we need such a channel at all, where are some errors?), Which means that the probability of two errors is less, and three are already quite small. We can choose for ourselves some acceptable amount of probability, outlining the boundary "this is certainly impossible." This will allow us to say that the channel may not be more than $$$k$ mistakes. This will be a characteristic of the communication channel.

For simplicity, we introduce the following notation. Let the data we want to transfer are binary sequences of fixed length. In order not to get entangled in zeros and units, we will sometimes denote them in capital Latin letters ( $$$A$ , $$$B$ , $$$C$ , ...). What exactly to transfer, in general, it does not matter, it will be easier to work with letters at first.

Encoding and decoding will be denoted by a straight arrow ( $$$\ rightarrow$ ), and the transmission over the communication channel - wavy arrow ( $$$\ rightsquigarrow$ ). Errors in the transmission will emphasize.

For example, suppose we want to send only messages. $$$A = 0$ and $$$B = 1$ . In the simplest case, they can be encoded with zero and one (surprise!):

$$

$$\ begin {aligned} A & \ to 0, \\ B & \ to 1. \ end {aligned}$$

The transmission on the channel in which the error occurred will be recorded as:

$$

$$A \ to 0 \ rightsquigarrow \ underline {1} \ to B.$$

Chains of zeros and ones with which we encode letters will be called code words. In this simple case, the code words are $$$0$ and $$$1$ .

Triple Code

Let's try to build some kind of correction code. What do we usually do when someone does not hear us? Repeat twice:

$$

$$\ begin {aligned} A & \ to 00, \\ B & \ to 11. \ end {aligned}$$

True, it does not help us much. In fact, consider a channel with one possible error:

$$

$$A \ to 00 \ rightsquigarrow 0 \ underline {1} \ to?$$

What conclusions can we draw when we received $$$01$ ? It is clear that since we do not have two identical numbers, it was a mistake, but in what category? Maybe in the first, and the letter was passed $$$B$ . And maybe in the second, and was transferred $$$A$ .

That is, the resulting code detects, but does not fix the error. Well, not bad either, in general. But we will go further and will now triple the numbers.

$$

$$\ begin {aligned} A & \ to 000, \\ B & \ to 111. \ end {aligned}$$

Check in:

$$

$$A \ to 000 \ rightsquigarrow 0 \ underline {1} 0 \ to A ?.$$

Got $$$010$ . Here we have two possibilities: either this $$$B$ and there were two mistakes (in extreme figures), either this $$$A$ and there was one mistake. In general, the probability of one error is higher than the probability of two errors, so the most plausible is the assumption that the letter was transmitted $$$A$ . Although plausible - does not mean true, so there is a question mark next to it.

If a maximum of one error is possible in the communication channel, then the first assumption of two errors becomes impossible and only one option remains - the letter was transmitted $$$A$ .

They say about such code that it fixes one mistake. He will also find two, but he will correct it incorrectly.

This is, of course, the easiest code. Encode is easy, and decode too. Zeroes more means zero passed, one means one.

If you think a little, you can offer a code correcting two errors. This will be the code in which we repeat the single bit 5 times.

Distances between codes

Let us consider the code with trebling in more detail. So, we got a working code that fixes a single error. But for all the good you have to pay: it encodes one bit in three. Not very effective.

And generally, why does this code work? Why is it necessary to triple to eliminate one error? Surely this is no accident.

Let's think about how this code works. Intuitively, everything is clear. Zeros and edinichki - these are two different sequences. Since they are quite long, a single error does not spoil their appearance.

May we transmit $$$000$ and got $$$001$ . It can be seen that this chain is more similar to the original $$$000$ than on $$$111$ . And since we have no other code words, the choice is obvious.

But what does “more like” mean? And everything is simple! The more characters in two chains coincide, the greater their similarity. If almost all characters are different, then the chains are “far away” from each other.

You can enter some value $$$d (\ alpha, \ beta)$ equal to the number of different digits in the corresponding bits of the chains $$$\ alpha$ and $$$\ beta$ . This value is called the Hamming distance. The greater this distance, the less like two chains.

For example, $$$d (010, 010) = 0$ , since all the numbers in the respective positions are equal, but $$$d (010101, 011011) = 3$ .

Hamming distance is called distance for a reason. After all, in fact, what is the distance? This is some characteristic indicating the proximity of two points, and for which the assertions are true:

1. The distance between the points is non-negative and is equal to zero only if the points coincide.
2. The distance in both directions is the same.
3. The path through the third point is not shorter than the straight path.

Reasonably reasonable requirements.

Mathematically, this can be written like this (it will not be useful to us, just for the sake of interest, let's see):

1. $$$d (x, y) \ geqslant 0, \ quad d (x, y) = 0 \ Leftrightarrow x = y;$
2. $$$d (x, y) = d (y, x);$
3. $$$d (x, z) + d (z, y) \ geqslant d (x, y)$ .

I suggest the reader to make sure that for the Hamming distance these properties are satisfied.

Neighborhood

Thus, we consider different chains as points in some imaginary space, and now we can find distances between them. True, if you try to arrange some long chains on a sheet of paper so that Hamming distances coincide with distances on a plane, we can fail. But do not worry. Yet this is a special space with its own laws. And words like "distance" only help us to reason.

Let's go further. Once we started talking about the distance, we can introduce such a thing as a neighborhood. As you know, a neighborhood of a point is a ball of a certain radius with a center in it. Ball? What other balls! We are talking about codes.

But it's simple. What is a ball? This is the set of all points that are not further from this point than a certain distance, called a radius. We have points, we have distance, now there are balls.

So let's say the neighborhood of the code word $$$000$ radius 1 - these are all codes that are at a distance not more than 1 from it, that is, differing not more than in one bit. That is, these codes:

$$

$$\ {000, 100, 010, 001 \}.$$

Yes, that's how strange the balls look in the code space.

And now look. Same all possible codes which we will receive in the channel in one error if we send $$$000$ ! This follows directly from the definition of a neighborhood. After all, each error causes the chain to change only in one digit, and therefore removes it at a distance of 1 from the original message.

Similarly, if two errors are possible in the channel, then sending some message $$$x$ , we get one of the codes that belongs to the neighborhood $$$x$ radius 2.

Then our entire decoding system can be built like this. We get some kind of chain of zeros and ones (a point in our new terminology) and look at the neighborhood of which code word does it fall.

How many errors can fix the code?

In order for the code to correct more errors, the surroundings must be as wide as possible. On the other hand, they should not intersect. Otherwise, if the point falls into the intersection area, it will be unclear to which neighborhood it belongs.

In code with doubling between code words $$$00$ and $$$11$ the distance is 2 (both digits are different). So, if we build around them balls of radius 1, then they will touch. This means that the touch point will belong to both balls and it will not be clear which of them it will be attributed to.

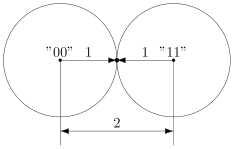
That is what we received. We saw that there was a mistake, but we could not fix it.

Interestingly, there are two contact points in our strange space of balls - these are codes $$$01$ and $$$10$ . The distances from them to the centers are equal to unity. Of course, in the usual geometry this is not possible, so the drawings are just a convention for more convenient reasoning.

In the case of a code with a tripling, there will be a gap between the balls.

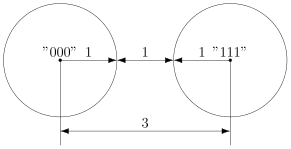
The minimum gap between the balls is 1, since our distances are always integer (well, two chains cannot differ in one and a half bits).

In general, we obtain the following.

This obvious result is actually very important. It means that the code with the minimum code distance $$$d _ {\ min}$ will work successfully in the channel with $$$k$ errors if the relation is

$$

$$d _ {\ min} \ geqslant 2k + 1.$$

The resulting equality makes it easy to determine how many errors a particular code will correct. And how much error code can detect? The arguments are the same. The code detects $$$k$ errors, if the result is not another code word. That is, code words should not be in the vicinity of the radius $$$k$ other code words. Mathematically, this is written like this:

$$

$$d _ {\ min} \ geqslant k + 1.$$

Consider an example. Suppose we encode 4 letters as follows.

$$

$$\ begin {aligned} A \ to 10100, \\ B \ to 01000, \\ C \ to 00111, \\ D \ to 11011. \\ \ end {aligned}$$

To find the minimum distance between different code words, we construct a table of pairwise distances.

	A	B	C	D
A	-	3	3	four
B	3	-	four	3
C	3	four	-	3
D	four	3	3	-

Minimum distance $$$d _ {\ min} = 3$ which means $$$3 \ geqslant2k + 1$ , whence we get that such code can fix up $$$k = 1$ mistakes. He discovers two errors.

Consider an example:

$$

$$A \ to 10100 \ rightsquigarrow 101 \ underline {1} 0.$$

To decode the received message, let's see which symbol it is closest to.

$$

$$\ begin {aligned} A: \, d (10110, 10100) & = 1, \\ B: \, d (10110, 01000) & = 4, \\ C: \, d (10110, 00111) & = 2, \\ D: \, d (10110, 11011) & = 3. \ end {aligned}$$

The minimum distance is for the character $$$A$ , it means that it was most likely transmitted by him:

$$

$$A \ to 10100 \ rightsquigarrow 101 \ underline {1} 0 \ to A ?.$$

So, this code corrects one error, as well as a code with a tripling. But it is more efficient, since, unlike the tripling code, 4 characters are encoded here.

Thus, the main problem when building such codes is to arrange the code words so that they are as far from each other as possible and there are more of them.

For decoding, it would be possible to use a table in which all possible received messages would be indicated, and the code words to which they correspond. But such a table would be very large. Even for our little code that gives out 5 binary digits, we’d get $$$2 ^ 5 = $ 3$ options for possible received messages. For more complex codes, the table will be much larger.

Let's try to think of a way to correct the message without tables. We can always find a useful application of the released memory.

Interlude: GF field (2)

To present further material, we will need matrices. And when multiplying matrices, as you know, we add and multiply the numbers. And there is a problem. If the multiplication is more or less good, then what about the addition? Due to the fact that we only work with single binary digits, it is not clear how to add 1 and 1 to get one binary digit again. So instead of the classical addition, you need to use something else.

We introduce the addition operation as an addition modulo 2 (well known to XOR programmers):

$$

$$\ begin {aligned} 0 + 0 & = 0, \\ 0 + 1 & = 1, \\ 1 + 0 & = 1, \\ 1 + 1 & = 0. \ end {aligned}$$

Multiplication will be done as usual. These operations are not actually introduced in any way, but in order to produce a system that is called a field in mathematics. A field is simply a set (in our case, from 0 and 1) on which addition and multiplication are defined so that the basic algebraic laws are preserved. For example, so that the basic ideas concerning matrices and systems of equations are still true. And we can introduce subtraction and division as inverse operations.

Set of two elements $$$\ {0, 1 \}$ with operations introduced as we did, it is called the Galois field GF (2). GF is the Galois field, and 2 is the number of elements.

In addition, there are some very useful properties that we will use in the future.

$$

$$x + x = 0.$$

This property follows directly from the definition.

$$

$$x + y = x - y.$$

And this can be seen by adding $$$y$ to both sides of equality. This property, in particular, means that we can transfer the terms in the equation to the other side without changing the sign.

We check the correctness

Let's go back to the code with trebling.

$$

$$\ begin {aligned} A & \ to 000, \\ B & \ to 111. \ end {aligned}$$

To begin, just solve the problem of checking whether there were any errors in the transmission. As can be seen from the code itself, the received message will be a code word only when all three digits are equal to each other.

Suppose we took a row vector $$$x$ of three digits. (We will not draw arrows above vectors, since we have almost everything - these are vectors or matrices.)

$$

$$\ dots \ rightsquigarrow x = (x_1, x_2, x_3).$$

Mathematically, the equality of all three digits can be written as a system:

$$

$$\ left \ {\ begin {aligned} x_1 & = x_2, \\ x_2 & = x_3. \ end {aligned} \ right.$$

Or, if we use the properties of addition in GF (2), we get

$$

$$\ left \ {\ begin {aligned} x_1 + x_2 & = 0, \\ x_2 + x_3 & = 0. \ end {aligned} \ right.$$

Or

$$

$$\ left \ {\ begin {aligned} 1 \ cdot x_1 + 1 \ cdot x_2 + 0 \ cdot x_3 & = 0, \\ 0 \ cdot x_1 + 1 \ cdot x_2 + 1 \ cdot x_3 & = 0. \ end {aligned} \ right.$$

In the matrix view, this system will be

$$

$$Hx ^ T = 0,$$

Where

$$

$$H = \ begin {pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \ end {pmatrix}.$$

Transposing here is necessary because $$$x$ Is a row vector, not a column vector. Otherwise we could not multiply it on the right by the matrix.

We will call the matrix $$$H$ check matrix. If the received message is a valid code word (that is, there was no transmission error), then the product of the check matrix on this message will be equal to the zero vector.

Multiplication by a matrix is ​​much more efficient than a search in a table, but we actually have another table — the coding table. Let's try to get rid of it.

Coding

So, we have a system for checking

$$

$$\ left \ {\ begin {aligned} x_1 + x_2 & = 0, \\ x_2 + x_3 & = 0. \ end {aligned} \ right.$$

Her decisions are code words. Actually, we built the system on the basis of code words. Now let's try to solve the inverse problem. By system (or, equivalently, by matrix $$$H$ ) find the code words.

However, for our system, we already know the answer, so that it would be interesting, we take another matrix:

$$

$$H = \ begin {pmatrix} 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 \ end {pmatrix}.$$

The corresponding system is:

$$

$$\ left \ {\ begin {aligned} x_1 + x_3 & = 0, \\ x_2 + x_3 + x_5 & = 0, \\ x_4 + x_5 & = 0. \ end {aligned} \ right.$$

To find the code words of the corresponding code you need to solve it.

By virtue of linearity, the sum of the two system solutions will also be the system solution. It is easy to prove. If a $$$a$ and $$$b$ - system solutions, then their sum is correct

$$

$$H (a + b) ^ T = Ha ^ T + Hb ^ T = 0 + 0 = 0,$$

which means she, too, is the solution.

Therefore, if we find all linearly independent solutions, then they can be used to obtain all the solutions of the system. To do this, just need to find their various amounts.

First we express all the dependent components. There are as many as equations. It is necessary to express so that on the right were only independent. The easiest way to express $$$x_1, x_2, x_4$ .

If we were not so lucky with the system, then we would have to add such a system by folding the equations together so that some three variables would occur once. Well, or use the Gauss method. For GF (2) it works too.

So, we get:

$$

$$\ left \ {\ begin {aligned} x_1 & = x_3, \\ x_2 & = x_3 + x_5, \\ x_4 & = x_5. \ end {aligned} \ right.$$

To obtain all linearly independent solutions, we equate each of the dependent variables to one in turn.

$$

$$\ begin {aligned} x_3 = 1, x_5 = 0: \ quad x_1 = 1, x_2 = 1, x_4 = 0 \ Rightarrow x ^ {(1)} = (1, 1, 1, 0, 0), \ \ x_3 = 0, x_5 = 1: \ quad x_1 = 0, x_2 = 1, x_4 = 1 \ Rightarrow x ^ {(2)} = (0, 1, 0, 1, 1). \ end {aligned}$$

The various sums of these independent solutions (namely, they will be code vectors) can be obtained as follows:

$$

$$a_1 x ^ {(1)} + a_2 x ^ {(2)},$$

Where $$$a_1, a_2$ equal to either zero or one. Since there are two such coefficients, then everything is possible $$$2 ^ 2 = 4$ combinations.

But look! The formula we just got is the multiplication of the matrix by the vector again.

$$

$$(a_1, a_2) \ cdot \ begin {pmatrix} 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 \ end {pmatrix} = aG.$$

The lines here are linearly independent solutions that we received. Matrix $$$G$ called generating. Now, instead of creating the coding table ourselves, we can get the code words by simple multiplication by the matrix:

$$

$$a \ to aG.$$

Find the code words for this code. (Do not forget that the length of the original messages must be equal to 2 - this is the number of solutions found.)

$$

$$\ begin {aligned} 00 & \ to 00000, \\ 01 & \ to 01011, \\ 10 & \ to 11100, \\ 11 & \ to 10111. \ end {aligned}$$

So, we have a ready-made code that detects errors. Check it in the case. Suppose we want to send 01 and we have an error in the transfer. Will the code find it?

$$

$$a = 01 \ to aG = 01011 \ rightsquigarrow x = 01 \ underline {1} 11 \ to Hx ^ T = (110) ^ T \ neq 0.$$

And if the result is not a zero vector, then the code is suspicious. To hold it failed. Hurray, the code works!

For the code with tripling, by the way, the generating matrix looks very simple:

$$

$$G=\begin{pmatrix}1&1&1\end{pmatrix}.$$

Such codes that can be generated and checked by a matrix are called linear (they are also non-linear), and they are very widely used in practice. Implementing them is fairly easy, since it only requires multiplication by a constant matrix.

, . !

, . , . $$$x$ , $$$v$ .

$$

$$e = x - v.$$

GF(2), , :

$$

$$\begin{aligned} v &= x + e,\\ x &= v + e. \end{aligned}$$

, , , , .

, $$$x$ , $$$Hx^T\neq 0$ . , ! , , ?

:

$$

$$s(x)=Hx^T.$$

$$

$$s(x) = Hx^T = H(v+e)^T = He^T = s(e).$$

, , .

, , . , . . ?

! , , , ? , , . .

, 5- . — .

$$$s(x)$	$$$x$
$$$000$	$$$\underline{00000}, 11100, 01011, 10111$
$$$001$	$$$\underline{00010}, 11110, 01001, 10101$
$$$010$	$$$\underline{01000}, 10100, 00011, 11111$
$$$011$	$$$01010, 10110, \underline{00001}, 11101$
$$$100$	$$$\underline{10000}, 01100, 11011, 00111$
$$$101$	$$$\underline{10010}, 01110, 11001, \underline{00101}$
$$$110$	$$$11000, \underline{00100}, 10011, 01111$
$$$111$	$$$11010, \underline{00110}, \underline{10001}, 01101$

, .

, . . , , .

, . , … .

$$

$$a=01 \to aG=01011 \rightsquigarrow x=01\underline{1}11 \to s(x)=Hx^T = (110)^T \to e=(00100).$$

$$$(00100)$ , which means an error in the third digit. As we made.

Hooray, everything works!

What next?

To practice, try repeating the reasoning for different test matrices. For example, for a code with trebling.

The logical continuation of the above would be a story about cyclic codes - an extremely interesting subclass of linear codes with remarkable properties. But then, I'm afraid, the article would really have grown.

If you are interested in the details, you can read the wonderful book Arshinov and Sadowski "Codes and Mathematics". It outlines much more than is presented in this article. If coding mathematics is of interest, then look at Blehut's Theory and Practice of Error Control Codes. In general, there are quite a lot of materials on this topic.

I hope that when there is free time again, I will write a sequel in which I will talk about cyclic codes and show an example of a program for encoding and decoding. Unless, of course, the venerable public is interested.