From two tuning forks from Lissajous experiments to a single elliptical level gauge tube with a step of centuries and everything in Python

Pictures from the network, the quality wants the best, but they quite accurately reflect the essence of the experience in visualizing figures. See the root is the basis of the wisdom of generations.
A bit of history
While still in school in physics class, I peered into an oscilloscope, on the screen of which, replacing each other, different figures appeared: first simple - line, parabola, circle, ellipse, then the figures became more and more saturated with continuous wavy lines, reminiscent of lace. The author of this lacy diva was Jules Antoine Lissajous, a French physicist, corresponding member of the Paris Academy of Sciences (1879) [1]. The figures themselves are closed trajectories, traced by a point that simultaneously performs two harmonic oscillations in two mutually perpendicular directions [2]. I think that in those years far from the present, the main merit of Jules, except for the course of knowledge of mathematics and physics, of course, was the simple mechanical visualization of these figures by improvised means. Like Zhulu, I wanted to construct as simply and visually as possible, to implement his ideas as applied to the modern linear measurement task. But to do this by mathematical modeling with graphical visualization of its results in Python. But first, consider the classic version [3] of building shapes.
')
What should be Lissajous figures
To do this, we use the system of equations describing the figures:
x (t), y (t) in the general case, time-dependent harmonic oscillations along mutually perpendicular planes, frequencies b, a, and initial phase d. For the analysis of figures in calculations, the modulus of the frequency difference | b - a | = 1. We consider the ratio of the circular frequencies b / a and the initial phase d. We have for the line A = B d = 0, a circle
Code for plotting each of the figures on separate graphs
#!/usr/bin/env python #coding=utf8 import numpy as np from numpy import sin,pi import matplotlib.pyplot as plt m=[[0],[2,2],[2,1],[1,2],[3,2],[3,4],[5,4],[5,6],[9,8]]# for i in m: if i[0]==0: a=1 x=[sin(a*t) for t in np.arange(0.,2*pi,0.01)] y=[sin(a*t) for t in np.arange(0.,2*pi,0.01)] plt.plot(x, y, 'r')# plt.grid(True) plt.show() else: a=i[0] b=i[1] d=0.5*pi x=[sin(a*t+d) for t in np.arange(0.,2*pi,0.01)] y=[sin(b*t) for t in np.arange(0.,2*pi,0.01)] plt.plot(x, y, 'r') # a/b # plt.grid (True) plt.show() I do not give the result, individual figures are not impressive. I want a collage of "lace".
Program code for plotting on one form of graphs for four figures with m = [3,4], [5,4], [5,6], [9,8]]
#!/usr/bin/env python #coding=utf8 import numpy as np from numpy import sin,pi import matplotlib.pyplot as plt m=[[3,4],[5,4],[5,6],[9,8]] # plt.figure(1) for i in m: a=i[0] b=i[1] d=0.5*pi x=[sin(a*t+d) for t in np.arange(0.,2*pi,0.01)] y=[sin(b*t) for t in np.arange(0.,2*pi,0.01)] if m.index(i)==0: plt.subplot(221) plt.plot(x, y, 'k') # a/b plt.grid(True) elif m.index(i)==1: plt.subplot(222) plt.plot(x, y, 'g') plt.grid(True) elif m.index(i)==2: plt.subplot(223) plt.plot(x, y, 'b') plt.grid(True) else: plt.subplot(224) plt.plot(x, y, 'r') plt.grid(True ) plt.show() And here they are "lace".
What can not be attributed to the Lissajous figures, by definition, about their isolation
Why do we need | b - a | = 1, “for the flags!” We try for example: m = [[1,3], [1,5], [1,7], [1,9]]
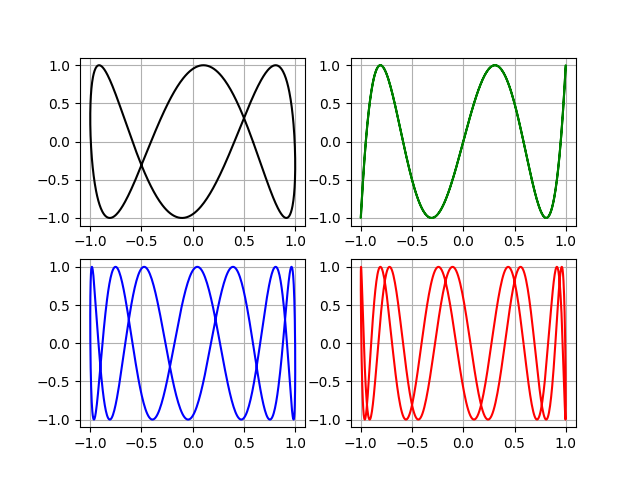
In the second graph, for m = 0.2, an open path was obtained, which, by definition, is not a Lbssage figure.
In search of mechanical analogs
Let us look for analogies of the figures in the measuring technique and here is a vibration level gauge with a resonator in the form of an elliptical tube [4].
Elastically fixed tube of elliptical cross section with the help of excitation systems 5,6,7 performs self-oscillations in one plane, and with the help of systems 8, 9, 10 in another plane perpendicular to the first one. The tube oscillates in two mutually perpendicular planes with different frequencies close to its own. The mass of the tube depends on the level of its filling fluid. With the change in mass, the oscillation frequencies of the tube also change, which are the output signals of the level gauge. Frequencies carry additional information about the multiplicative and additive additional errors that are compensated by the processing of frequencies by the microprocessor 11.
Conditions for adequate modeling
In order to more or less correctly link the Lissajous figures to the work of the mentioned level gauge, the following circumstances should be taken into account. First, an elliptical tube fixed at one end is an oscillating system with distributed parameters, which greatly complicates the analysis of its oscillations. Secondly, the ratio of the oscillation frequencies of the tube can not change arbitrarily, it depends on the ellipticity of the cross section and the allowable gaps in the system of excitation of oscillations. For the frequency ratio, you can get a simple ratio.
What variables belong to, a, b, a0, b0 is clear from the figure and, moreover, the formula for the cyclical frequency of the oscillator is known from the school physics course. To “implement in Python, in the last relation, we introduce the wall thickness and the ellipse index of the internal section of the tube; then, instead of four variables, we get three.
The program code to determine. allowable frequency ratio change
#!/usr/bin/env python #coding=utf8 import numpy as np from numpy import sqrt import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' d=0.5 a=9 x=[w for w in np.linspace(0.8,0.95,15)] y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)] plt.plot(x, y, 'r', label=' . -- %s' %str(d)) d=0.7 y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)] plt.plot(x, y, 'b',label=' .-- %s' %str(d)) d=1.0 y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)] plt.plot(x, y, 'g', label=' .-- %s' %str(d)) plt.ylabel(' ') plt.xlabel(' ') plt.title(' ') plt.legend(loc='best') plt.grid(True) plt.show() As a result of the program, we get the schedule.

The graph is constructed for a small inner axis of 9 mm. For a constructively acceptable ratio of small to large semi-axis in the range from 0.8 to 0.95. This is the main factor affecting the frequency ratio, which varies from 1.18 to 1.04. Wall thickness is affected slightly. Now we have a range of relationships and can be used for further modeling.
Oscillations of the vertical axis of the tube
As for the distributed mechanical parameters of the cantilever tube, they can be reduced to a concentrated stiffness mass and damping with the help of equality of natural frequencies and impedance. In addition, to determine the forms of bending vibrations of a cantilever tube, an expression for distributed parameters can be obtained. The equation for forms - beam functions has the form:
Where
It should be noted that, in spite of the large number of publications on the shapes and frequencies of oscillations of a cantilever rod, a beam or tube, equations (4) are not given anywhere, only pictures without coordinates. Therefore, equation (4), I derived through the conditions at the ends and the beam functions, checked by the roots (5) and the location of the nodes. However, this is a trivial equation, which is simply forgotten.
Program code for the numerical determination of the roots of equation 1.1 and the construction of three forms of flexural vibrations of the tube axis
1.1 - 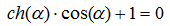
#!/usr/bin/env python #coding=utf8 from scipy.optimize import * import numpy as np from numpy import pi,cos,cosh,sin,sinh import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' d=[] for i in range(0,4): x=brentq(lambda x:cosh(x)*cos(x)+1,0+pi*i,pi+pi*i) p=round(x,3) if p not in d: d.append(p) x=[w for w in np.linspace(0,1,100)] k=d[0] z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x) )for x in np.linspace(0,1,100)] plt.plot(z, x, 'g', label=' - %s' %str(k)) k=d[1] z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x)) for x in np.linspace(0,1,100)] plt.plot(z, x, 'b', label=' - %s' %str(k)) k=d[2] z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x)) for x in np.linspace(0,1,100)] plt.plot(z, x, 'r', label=' - %s' %str(k)) plt.title(' ') plt.xlabel(' OX ') plt.ylabel(' OZ ') plt.legend(loc='best') plt.grid(True) plt.show() As a result of the work of the program, we obtain a graph constructed with regard to the vertical position of the tube.

On the graph, the coordinate of the centerline is shown to the length of the tube, and the amplitude is normalized. The position of the tube vibration nodes relative to the place of its attachment corresponds exactly to the vibration theory.
What are the trajectories moving end of the tube
The last obstacle is the difficulty of obtaining a meaningful numerical solution of the differential oscillation equations, subject to varying by several parameters simultaneously. Here came two of my articles on the oscillatory link in Python [5, 6], which provide a method for obtaining exact symbolic solutions of differential equations.
We write two conditionally independent equations for tube oscillations in the OX and OY plane with different frequencies a and b, the relationship between which is selected from the previously established range. The remaining parameters are selected in the correct relationship, but arbitrarily to better demonstrate the result.
The following notation is introduced here (for simplicity, without indices).
Program code for solving each differential equation of system (6), followed by addition to obtain the trajectory of the end of the tube.
import numpy as np from sympy import * from IPython.display import * import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' def solution(w,v,i,n1,n2,B,f,N): t=Symbol('t') var('t C1 C2') u = Function("u")(t) de = Eq(u.diff(t, t) +2*B*u.diff(t) +w**2* u, f*sin(w*t+v)) des = dsolve(de,u) eq1=des.rhs.subs(t,0) eq2=des.rhs.diff(t).subs(t,0) seq=solve([eq1,eq2],C1,C2) rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])]) g= lambdify(t, rez, "numpy") t= np.linspace(n1,n2,N) plt.figure(1) if i==1: plt.subplot(221) plt.plot(t,g(t),color='b', linewidth=3,label='x=%s*sin(%s*t+%s)' %(str(f),str(w),str(v))) plt.legend(loc='best') plt.grid(True) else: plt.subplot(222) plt.plot(t,g(t),color='g', linewidth=3,label='y=%s*sin(%s*t+%s)' %(str(f),str(w),str(v))) plt.legend(loc='best') plt.plot(t,g(t),color='r', linewidth=3) plt.grid(True) return g(t) N=1000# B=0.2# f=1# n1=0# n2=20# w1=5.0# w2=10.0# v1=0# v2=0# g1=solution(w1,v1,1,n1,n2,B,f,N) g2=solution(w2,v2,2,n1,n2,B,f,N) plt.subplot(223) plt.plot(g1,g2,color='b', linewidth=3,label='w1/w2=%s'%str(w1/w2)) plt.legend(loc='best') plt.grid(True) plt.subplot(224) x=[w for w in np.linspace(0,1,100)] k=1.875 z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x) )for x in np.linspace(0,1,100)] plt.plot(z, x, 'g',label=' -%s'%str(k)) plt.legend(loc='best') plt.grid(True) plt.show() The program allows you to change all the parameters of the model, for example, for:
N = 1000, B = 0.2, f = 1, n1 = 0, n2 = 20, w1 = 5.0, w2 = 10.0, v1 = 0, v2 = 0
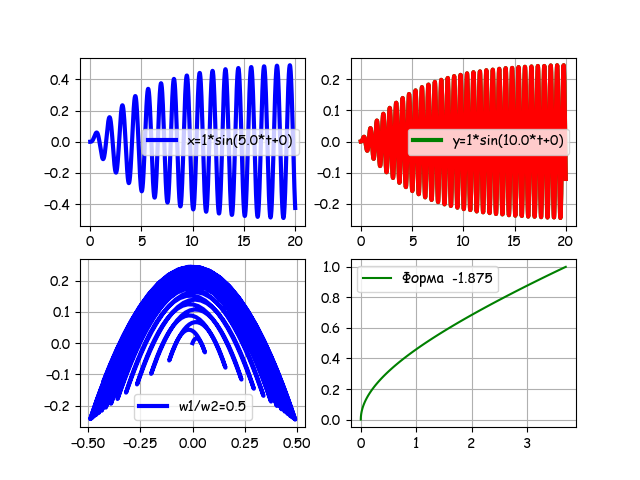
For a frequency ratio of 0.5, the transient multiplies the shapes. Put the "gate" of time n15 = 0, n2 = 20, we get.

Remove the "gate" and enter the initial phase v2 = -pi / 2, we get:
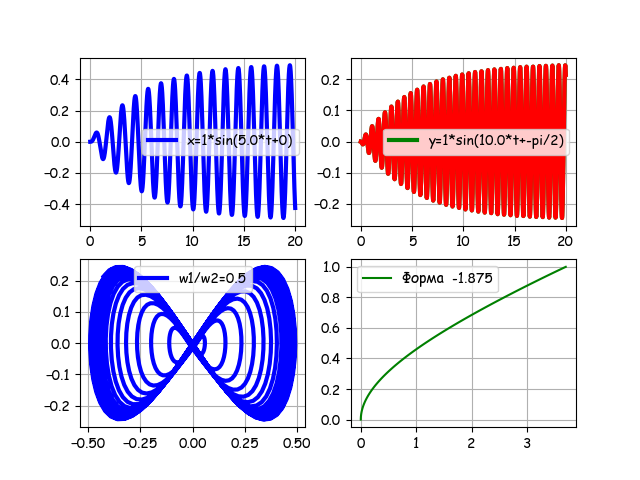
Taking into account the foregoing, I do not require commentary graphics.
For intrigue
If this article finds its readers or readers find it without fearing the shadows of the past, then I will publish three-dimensional animated graphs of complex spatial oscillations of the tube as the filling fluid level changes in it.
Instead of conclusions
The invention of Jules Antoine Lissajous continues its journey in time, but already in Python. I hope that the presented interpretation, certainly far from perfect, will allow us to continue acquaintance with the works of the brilliant mathematician Lissajous.
Links
Source: https://habr.com/ru/post/327768/
All Articles