Mersenne prime numbers and Luke-Lemer test

Translation of the post by John McGee (John McGee) " Mersenne Primes and the Lucas – Lehmer Test ".
The code given in the article can be downloaded here .
I express my deep gratitude to Polina Sologub for assistance in translating and preparing the publication .
Content
- Introduction.
- The Euler and Mersenne multiplier theorem
- Luke and Lemer
- From before
- perfect numbers
- 21st, 22nd and 23rd numbers of Mersenne
- 24th, 25th and 26th of Mersenne.
- 27th and 28th of Mersenne
- 29th number of Mersenne
- 30th and 31st of Mersenne
- Great online search for Mersenne numbers
- Factorization of Mersenne numbers
')
Introduction
Mersenne Prime Number - a Prime Number (the value of the degree of p should also be simple). These prime numbers got their name from the name of the French mathematician and religious scholar Mersenne , who made this list of prime numbers of this form in the first half of the seventeenth century. The first four of them have been known for a long time: , , and .
Mersenne argued that the value will be simple for prime numbers belonging to the set . Whether he was right in everything, you can check with the Wolfram Language - PrimeQ function , which uses modern methods of testing numbers for simplicity, which do not require searching for a specific multiplier to prove that the number is composite.


It is possible that his statement that - a prime number, just a typo, and in fact he meant . It is easy to understand that the test of simplicity was difficult for Mersenn during his life, because the test by division was one of the few tools available. For example, for the smallest factor is a 15-digit number, so even with modern methods of factorization it is not so easy to find. The FactorInteger function uses the most advanced methods that allow you to apply the factorization method for large integers.
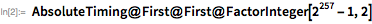

Euler and Mersenne multiplier theorem
The first important achievements in the field of simplicity testing belong to the great mathematician Leonard Euler , who, shortly before 1772, clarified that is simple. He did this by demonstrating that any simple divisor must be equal to 1 or 62 (mod 248).
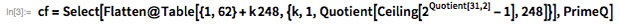

Such a relatively short list, even in the times of Euler, could be checked using test division (manually). He belongs to the application of the theorem of Mersenne , which states that if is a divider then , and for some positive integer . These facts significantly limit the number of possible dividers. . Using the functions presented below, the use of this theorem is demonstrated to provide a list of possible divisors. smaller than .
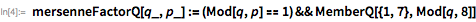
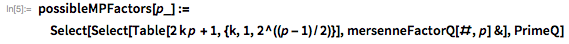


We use these functions to quickly find a divider. . note that is a divider then and only if . This makes it possible to use the PowerMod function, which ensures effective exponentiation modulo.
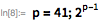
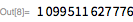


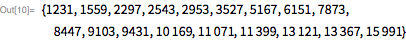

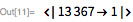
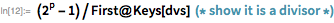
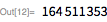
The following is the number of Mersenne with 161649 characters :.


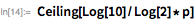


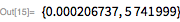
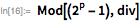

Luke and Lemer
The next important step was the discovery by Edward Luke of a method for checking the simplicity of the numbers of this form. He used his method in 1876 to check whether (the largest number of Mersenne pre-computer era) simple. In the early twentieth century, when the basics of binary arithmetic and algebra became widely known, Derek Henry Lemer improved the method of Luke. The resulting simplicity test of Luc-Lemer provided an effective check if the number of this form was simple. The test was carried out using the comparison module:

It means that identical to the number represented by its bits of the lower order, plus - the numbers represented by the other bits. This relationship can be applied recursively as long as .
Consider the following example. Here we show that
 for . note that
for . note that  (23 lower order bits) and
(23 lower order bits) and  - means that the remaining bits are shifted to the lowest position.
- means that the remaining bits are shifted to the lowest position.

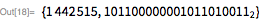
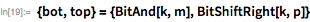



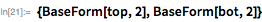
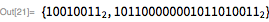

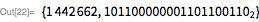
The function below sets this method to calculate using only bit operations (no division). Note that has binary form , while there is no 0, and therefore it also serves as a mask for lower order bits .

The following function implements the Luke-Lemere simplicity test (LLT). Determine the sequence , . Then is simple if and only if .

Experience shows that the main execution time of these functions is spent on integer arithmetic.
To check whether simple, it is better to first check the simplicity on small prime dividers and perform other checks of simplicity. First, we use the Mersenne prime divisor theorem encoded in checkMPDivisors , and then the PrimeQ function. If this does not work, apply the Luke-Lemer test.

Here we present an extended version of PrimeQ , which applies the Luke- Lemere test for large numbers .

From before
The first prime number of Mersenne, discovered on a computer using the Luke-Lemer test, was , found by Rafael Robinson on January 30, 1952 based on the SWAC (Standards Western Automatic Computer) tube computer. Below you see a block of memory of this computer, containing 256 words of 37 bits each.

The 20th Mersenne prime number was discovered by Alexander Hurwitz in November 1961 as a result of Luke-Lemer’s 50-minute test on the IBM 7090. Below we reproduce these results (this took about 151 seconds of computer time on a modern single-core laptop).







One of the features of the Wolfram Language that makes it suitable for this kind of work is its fast integer arithmetic. The search for Mersenne primes was a real challenge at the dawn of the era of computerized search. Researchers adapted fast Fourier transform methods to transform the problem of multiplying two large integers into a simple, element-wise product of transformed digits. Fast multiplication of integers is necessary for the squaring step in the Luc-Lemer test. The Wolfram Language uses the latest algorithms optimized to work with exact integers with billions of characters. For example, make sure that the last one, - , Is in fact a simple Mersenne number, and we will demonstrate all its numbers.



Perfect numbers
There is an interesting connection between prime Mersenne numbers and perfect numbers. A perfect number is a number equal to the sum of all its divisors (different from the number itself). Euclid assumed, and Euler proved that all even perfect numbers have the form . The Wolfram Language PerfectNumberQ function checks if the number is perfect. Let us demonstrate this property on .
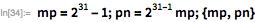

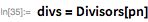


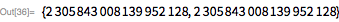


21st, 22nd and 23rd numbers of Mersenne
Let us turn to the re-discovery of the 21st, 22nd and 23rd numbers of Mersenne (we will denote them further in the form of ): , , . All of them were discovered by Donald Gillis, who ran the LLT on ILLIAC II throughout the spring of 1963 (see here ). To check all numbers of the form for prime numbers in between it took us about 6 minutes.


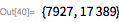

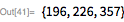
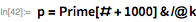



24th, 25th and 26th numbers of Mersenne
Next, we expand the search to find , , . The last of them was discovered in February 1979 by Landon Kurt Noll and Laura Nickel. They searched in range from before on the CDC Cyber 174 supercomputer (you can read about it here ). Our calculations become longer, so we start using parallel processing. Since the tests are independent, we can use ParallelMap to speed up the work. Range check takes about three and a half minutes (4 cores are used).



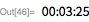
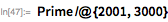
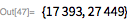


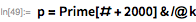
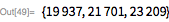
Note that Luke- Lemere's specialized test is significantly faster than the more general PrimeQ function (for given Mersenne numbers).

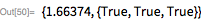
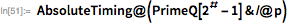

27th and 28th of Mersenne
Next we checked the range to find the number . It was discovered in April 1979 by Harry Nelson and his team (they used the Cray-1 supercomputer). Our search was completed in 15 minutes.


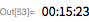
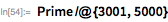


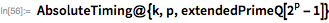
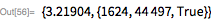
The next number is mersenne, . It was opened in September 1982 by David Slowinski - also on Cray-1. This supercomputer weighed about 5 tons and consumed about 115 kilowatts of electricity, and its computing performance reached 160 megaflops . It came with 1 million 64-bit words of memory (8 megabytes), and cost about $ 16000000 in today's prices. The detail of its cooling system is shown below. For comparison, the Raspberry Pi weighs a few ounces, runs at 4 watts, provides about 410 megaflops and is equipped with 1GB of RAM, and that’s all for $ 40. And it comes immediately with Mathematica .


Number contains 25962 digits. We found this value in 1 hour and 14 minutes (on my laptop, not on the Raspberry Pi), conducting tests in the range .



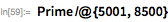





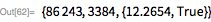
29th number of mersenne
Since we now need more serious computer time, we also produce a time stamp for each run. Now we check the range . After 1 hour and 44 minutes, the computer showed: . This number was first discovered on January 29, 1988 by Walker Colquitt and Luke Welch (NEC DX-2 supercomputer; article can be found here ).
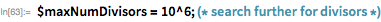






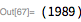




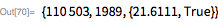


30th and 31st of mersenne
The following are two Mersenne prime numbers: and , - were actually discovered even before the 29th (by the same team that found the 28th). They used Cray X-MP to find the 30th number of Mersenne in September 1983 and the 31st in September 1985. Check using the range search function . To check each in this range it took 4 hours and 8 minutes.








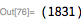

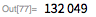

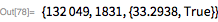


Great online search for Mersenne numbers
With the discovery of the 34th prime number of Mersenne - - in September 1996, the era of supercomputers for searching for Mersenne primes was over. The following 15 were found by volunteers of the Great Internet Search for Mersenne Prime Numbers ( GIMPS ), which include the Luke-Lemer test variant (as a background process) on personal computers. This large-scale distributed computing project currently reaches a performance level equivalent to about 300 teraflops per second, with downtime of more than 1.3 million computers.

Check the 34th of Mersenne with the Luke-Lemer test. At this stage, we have reached the limit of the possibilities of a personal computer. Testing thousands of Mersenne numbers in this range will take many days. It is interesting to note that the Luke-Lemere test is often used as a stress test for the reliability of computer hardware and software, since even one arithmetic error among the billions of calculations required to test one large prime number would entail an incorrect conclusion, which would mean a loss Mersenne numbers or false answer. The fact that we checked every for primes between 2 and 139901, convincingly proves the reliability of the arithmetic of large numbers and binary operations in the Mathematica system and the Wolfram Language.
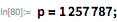


Mersenne number factorization
As we have already seen, the number of possible factors in the expansion of numbers of the form according to the theorem of multipliers, Mersenne is limited. This allowed for an effective computerized search for the divisors of large numbers of this form. At the time of this writing, all Mersenne numbers (up to ) were fully factorized (illustrations can be found here ). The GIMPS project also led to the discovery of the large multipliers of many Mersenn numbers as a by-product of checking the simplicity of numbers. A new article, which is a modern approach to solving this problem (along with 17 new factorizations), can be found here . The largest factorized number was ; its smallest divisor found has 76 decimal digits. Its smallest divider is 23. The total time required to get this result is 7500 years (talking about computer time).
We can quickly find the first few factors. using the FactorInteger function.


All the Mersenne prime numbers found to date are cataloged in the Wolfram Language (before the 44th). Access to this information is provided by the MersennePrimeExponent and MersennePrimeExponentQ functions.
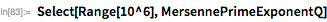





If you are interested in this topic, you can find more information on the following websites:
Source: https://habr.com/ru/post/327342/
All Articles