Open machine learning course. Topic 9. Time Series Analysis with Python
Good day! We continue our series of open-source machine learning articles and today we will talk about time series.
 Let's look at how to work with them in Python, what possible methods and models can be used for forecasting; what is double and triple exponential weighting; what to do if stationarity is not about you; how to build SARIMA and not die; and how to predict xgboost. And all this we will apply for example from the harsh reality.
Let's look at how to work with them in Python, what possible methods and models can be used for forecasting; what is double and triple exponential weighting; what to do if stationarity is not about you; how to build SARIMA and not die; and how to predict xgboost. And all this we will apply for example from the harsh reality.
UPD: now the course is in English under the brand mlcourse.ai with articles on Medium, and materials on Kaggle ( Dataset ) and on GitHub .
Video recording of the lecture based on this article as part of the second launch of the open course (September-November 2017).
- Primary data analysis with Pandas
- Visual data analysis with Python
- Classification, decision trees and the method of nearest neighbors
- Linear classification and regression models
- Compositions: bagging, random forest. Validation and training curves
- Construction and selection of signs
- Teaching without a teacher: PCA, clustering
- We study on gigabytes with Vowpal Wabbit
- Time Series Analysis with Python
- Gradient boosting
Plan for this article:
- Moving, smoothing and evaluating
- Rolling window estimations
- Exponential Smoothing, Holt-Winters Model
- Cross-validation on time series, selection of parameters
- Econometric approach
- Stationarity, single roots
- We get rid of non-stationarity and build SARIMA
- Linear and not very time series models
- Feature Extraction
- Linear regression vs XGBoost
- Homework
- Useful resources
Introduction
At work, I almost daily encounter various tasks related to time series. The most common question arises - what will happen to our indicators in the next day / week / month / etc. - how many players will install the applications, how many will be online, how many actions will be performed by users, and so on. The forecasting task can be approached differently, depending on what quality the forecast should be for, for what period we want to build it, and, of course, for how long it is necessary to select and adjust the model parameters to obtain it.
Let's start with simple methods of analysis and forecasting - moving averages, smoothing and their variations.
Moving, smoothing and evaluating
A small definition of the time series:
A time series is a sequence of values describing a process occurring in time, measured at successive times, usually at regular intervals.
Thus, the data are ordered with respect to non-random moments of time, and, therefore, unlike random samples, they can contain additional information that we will try to extract.
We import the necessary libraries. Basically, we will need the statsmodels module, which implements numerous methods of statistical modeling, including for time series. For fans of R who have moved to Python, it may seem very familiar, since it supports the writing of wording models in the style of 'Wage ~ Age + Education'.
import sys import warnings warnings.filterwarnings('ignore') from tqdm import tqdm import pandas as pd import numpy as np from sklearn.metrics import mean_absolute_error, mean_squared_error import statsmodels.formula.api as smf import statsmodels.tsa.api as smt import statsmodels.api as sm import scipy.stats as scs from scipy.optimize import minimize import matplotlib.pyplot as plt As an example for the work, let's take the real data on the hour online players in one of the mobile toys:
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot from plotly import graph_objs as go init_notebook_mode(connected = True) def plotly_df(df, title = ''): data = [] for column in df.columns: trace = go.Scatter( x = df.index, y = df[column], mode = 'lines', name = column ) data.append(trace) layout = dict(title = title) fig = dict(data = data, layout = layout) iplot(fig, show_link=False) dataset = pd.read_csv('hour_online.csv', index_col=['Time'], parse_dates=['Time']) plotly_df(dataset, title = "Online users") 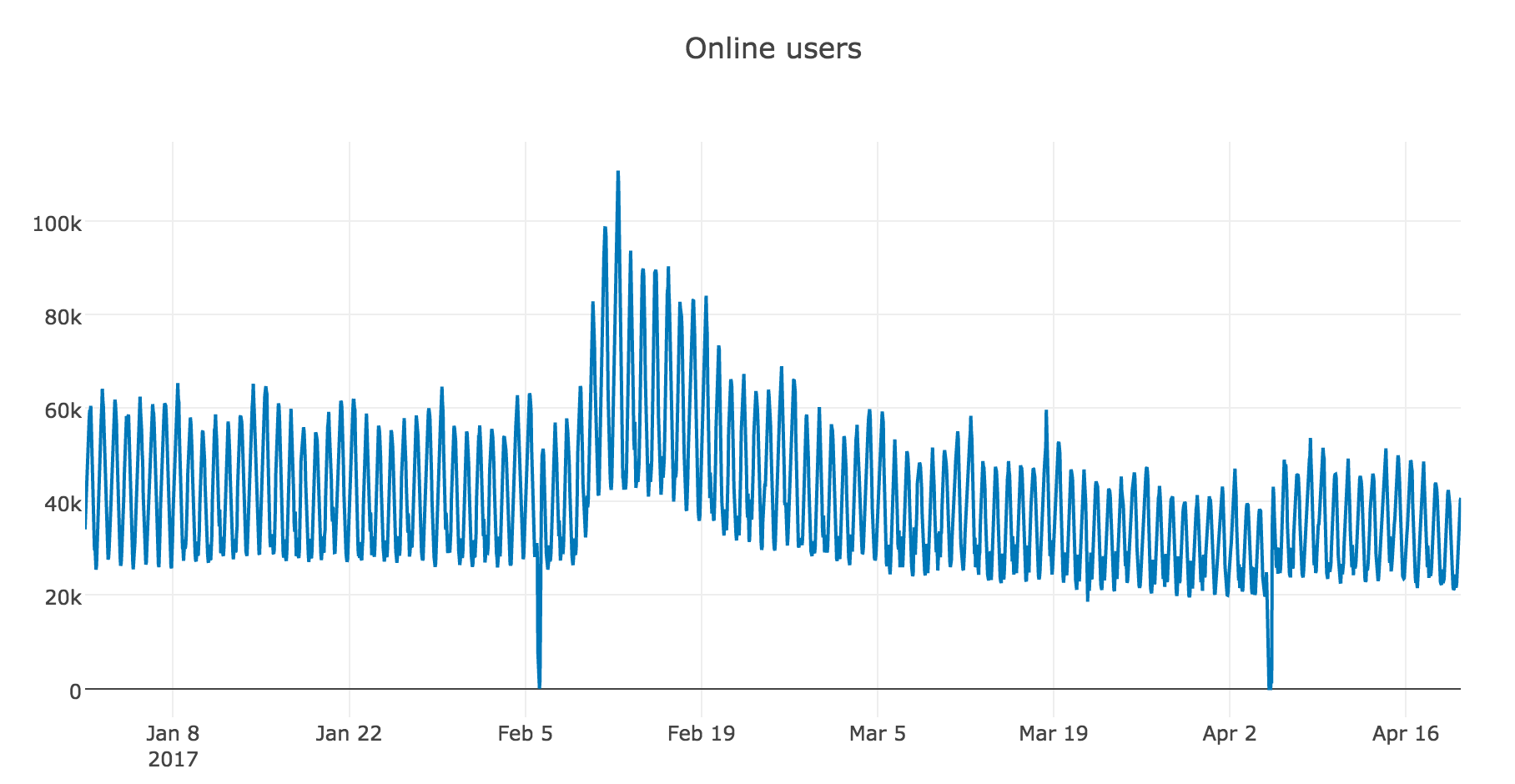
Rolling window estimations
Let's start modeling with the naive assumption - “tomorrow will be like yesterday”, but instead of a model of the form we will assume that the future value of the variable depends on the average its previous values, which means we use the moving average .
We implement the same function in python and look at the forecast, built on the last observed day (24 hours)
def moving_average(series, n): return np.average(series[-n:]) moving_average(dataset.Users, 24) Out: 29858.333333333332 Unfortunately, such a long-term forecast cannot be made - in order to get a prediction one step further, the previous value should be an actually observed value. But the moving average has another application - smoothing the original series to identify trends. There is a ready implementation in the DataFrame.rolling(window).mean() - DataFrame.rolling(window).mean() . The more we set the width of the interval, the more smooth the trend will be. If the data is very noisy, which is especially common, for example, in financial indicators, such a procedure can help with the definition of common patterns.
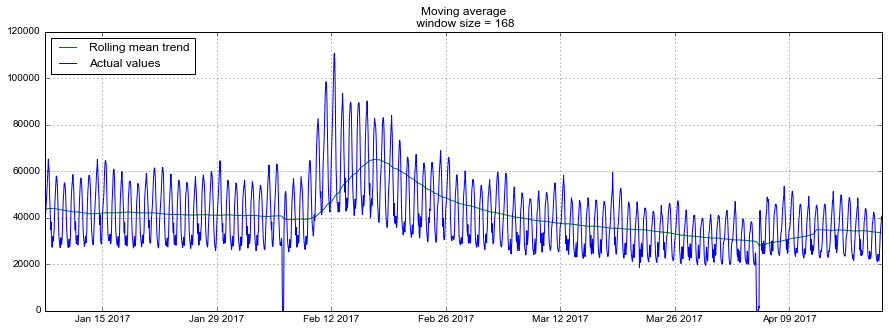
For our series, trends are quite obvious, but if we smooth them out by day, the online dynamics are better visible on weekdays and weekends (weekends - it's time to play), and weekly smoothing reflects well the general changes associated with a sharp increase in the number of active players in February and the subsequent decline in March.
def plotMovingAverage(series, n): """ series - dataframe with timeseries n - rolling window size """ rolling_mean = series.rolling(window=n).mean() # , #rolling_std = series.rolling(window=n).std() #upper_bond = rolling_mean+1.96*rolling_std #lower_bond = rolling_mean-1.96*rolling_std plt.figure(figsize=(15,5)) plt.title("Moving average\n window size = {}".format(n)) plt.plot(rolling_mean, "g", label="Rolling mean trend") #plt.plot(upper_bond, "r--", label="Upper Bond / Lower Bond") #plt.plot(lower_bond, "r--") plt.plot(dataset[n:], label="Actual values") plt.legend(loc="upper left") plt.grid(True) plotMovingAverage(dataset, 24) # plotMovingAverage(dataset, 24*7) # 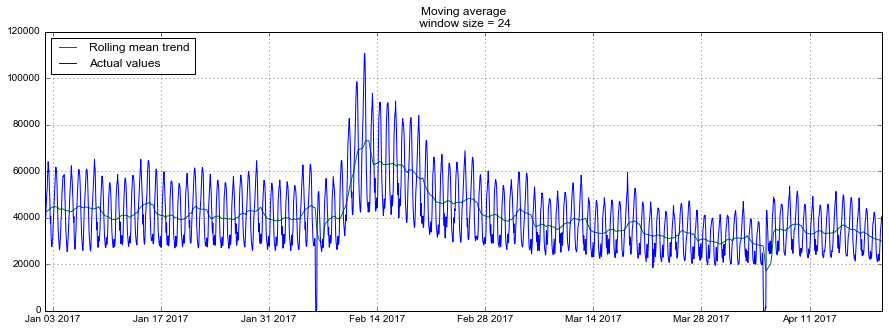
A modification of a simple moving average is a weighted average , within which various weights are attached to the observations, giving a total of one in the total, with more weight being usually assigned to the last observations.
def weighted_average(series, weights): result = 0.0 weights.reverse() for n in range(len(weights)): result += series[-n-1] * weights[n] return result weighted_average(dataset.Users, [0.6, 0.2, 0.1, 0.07, 0.03]) Out: 35967.550000000003 Exponential Smoothing, Holt-Winters Model
Simple exponential smoothing
Now let's see what happens if instead of weighing the last the values of the series, we begin to weigh all available observations, while decreasing weights exponentially as we go deeper into the historical data. The simple exponential smoothing formula will help us with this:
Here, the model value is a weighted average between the current true and previous model values. Weight called a smoothing factor. It determines how quickly we will “forget” the last available true observation. The smaller , the more influences previous model values have, and the series are smoothed out more.
Exponentiality is hidden in the recursiveness of a function - every time we multiply to the previous model value, which, in turn, also contained and so on until the very beginning.
def exponential_smoothing(series, alpha): result = [series[0]] # first value is same as series for n in range(1, len(series)): result.append(alpha * series[n] + (1 - alpha) * result[n-1]) return result with plt.style.context('seaborn-white'): plt.figure(figsize=(20, 8)) for alpha in [0.3, 0.05]: plt.plot(exponential_smoothing(dataset.Users, alpha), label="Alpha {}".format(alpha)) plt.plot(dataset.Users.values, "c", label = "Actual") plt.legend(loc="best") plt.axis('tight') plt.title("Exponential Smoothing") plt.grid(True) 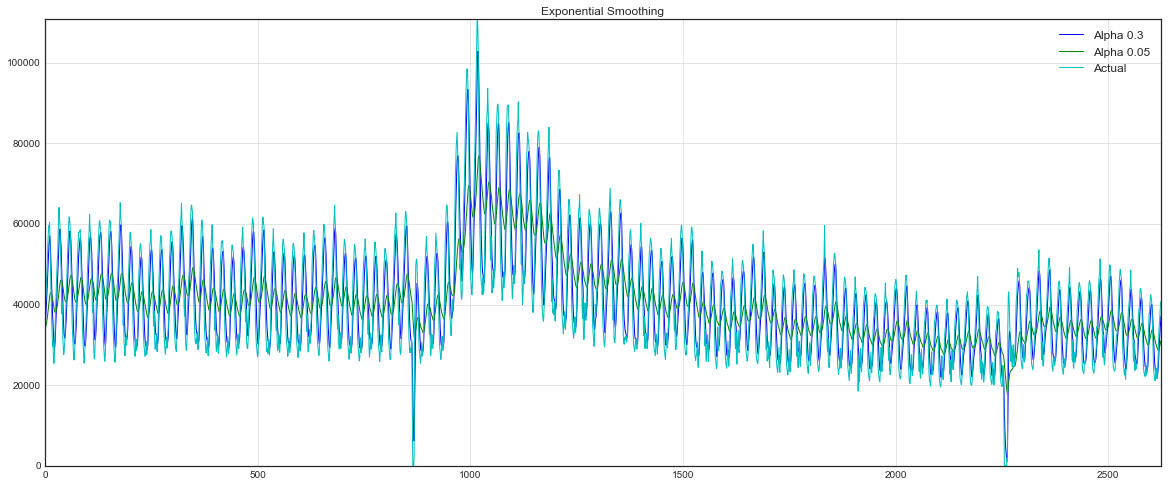
Double exponential smoothing
Until now, we could get a forecast just one point ahead (and even smooth the series nicely) from our methods at best. This is great, but not enough, so let's move on to expanding the exponential smoothing, which will allow us to build a forecast two points ahead (and too beautiful to smooth out the series).
This will help us split the series into two components - level (level, intercept) and trend (trend, slope). We predicted the level, or the expected value of the series, using the previous methods, and now the same exponential smoothing is applicable to the trend, naively or not very well believing that the future direction of change of the series depends on the weighted previous changes.
The result is a set of functions. The first describes the level - it, as before, depends on the current value of the series, and the second term is now divided into the previous value of the level and trend. The second is responsible for the trend - it depends on the level change at the current step, and on the previous trend value. Here, the role of weight in the exponential smoothing is the coefficient . Finally, the final prediction is the sum of the model level and trend values.
def double_exponential_smoothing(series, alpha, beta): result = [series[0]] for n in range(1, len(series)+1): if n == 1: level, trend = series[0], series[1] - series[0] if n >= len(series): # value = result[-1] else: value = series[n] last_level, level = level, alpha*value + (1-alpha)*(level+trend) trend = beta*(level-last_level) + (1-beta)*trend result.append(level+trend) return result with plt.style.context('seaborn-white'): plt.figure(figsize=(20, 8)) for alpha in [0.9, 0.02]: for beta in [0.9, 0.02]: plt.plot(double_exponential_smoothing(dataset.Users, alpha, beta), label="Alpha {}, beta {}".format(alpha, beta)) plt.plot(dataset.Users.values, label = "Actual") plt.legend(loc="best") plt.axis('tight') plt.title("Double Exponential Smoothing") plt.grid(True) 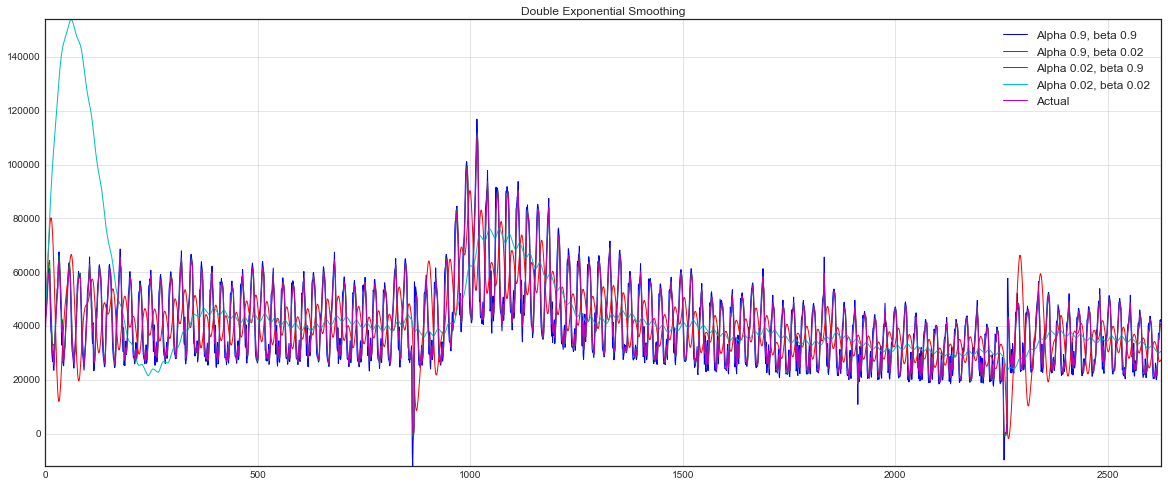
Now I had to configure two parameters - and . The first is responsible for smoothing the series around the trend, the second - for smoothing the trend itself. The higher the values, the more weight will be given to the latest observations and the less smoother the model range will be. Combinations of parameters can produce quite bizarre results, especially if asked by hand. And about not manual selection of parameters I will tell a little lower, immediately after the triple exponential smoothing.
Triple exponential smoothing aka Holt-Winters
So, successfully reached the next option of exponential smoothing, this time triple.
The idea of this method is to add another, third, component - seasonality. Accordingly, the method is applicable only if the series is not deprived of this seasonality, which is true in our case. The seasonal component in the model will explain the repeated fluctuations around the level and trend, and it will be characterized by the length of the season — the period after which the repetitions of the oscillations begin. For each observation in the season, its component is formed, for example, if the season length is 7 (for example, weekly seasonality), then we get 7 seasonal components, piece by piece for each of the days of the week.
We get a new system:
The level now depends on the current value of the series minus the corresponding seasonal component, the trend remains unchanged, and the seasonal component depends on the current value of the series minus the level and on the previous value of the component. In this case, the components are smoothed over all available seasons, for example, if this is a component responsible for Monday, then it will be averaged only with other Mondays. More information about the work of averages and an assessment of the initial values of the trend and seasonal components can be found here . Now, having a seasonal component, we can predict not just one, or even two, but arbitrary steps forward, which can not but rejoice.
Below is the code for building a model of triple exponential smoothing, also known by the names of its creators - Charles Holt and his student Peter Winters.
Additionally, Brutlaga method is included in the model for building confidence intervals:
$$ display $$ \ hat y_ {max_x} = \ ell_ {x − 1} + b_ {x − 1} + s_ {x − T} + m⋅d_ {t − T} \\ \ hat y_ {min_x} = \ ell_ {x − 1} + b_ {x − 1} + s_ {x − T} -m⋅d_ {t − T} \\ d_t = \ gamma∣y_t− \ hat y_t∣ + (1− \ gamma ) d_ {t − T}, $$ display $$
Where - season length, - the predicted deviation, and the remaining parameters are taken from the triple smoothing. More information about the method and its application to the search for anomalies in the time series can be found here.
class HoltWinters: """ - https://fedcsis.org/proceedings/2012/pliks/118.pdf # series - # slen - # alpha, beta, gamma - - # n_preds - # scaling_factor - ( 2 3) """ def __init__(self, series, slen, alpha, beta, gamma, n_preds, scaling_factor=1.96): self.series = series self.slen = slen self.alpha = alpha self.beta = beta self.gamma = gamma self.n_preds = n_preds self.scaling_factor = scaling_factor def initial_trend(self): sum = 0.0 for i in range(self.slen): sum += float(self.series[i+self.slen] - self.series[i]) / self.slen return sum / self.slen def initial_seasonal_components(self): seasonals = {} season_averages = [] n_seasons = int(len(self.series)/self.slen) # for j in range(n_seasons): season_averages.append(sum(self.series[self.slen*j:self.slen*j+self.slen])/float(self.slen)) # for i in range(self.slen): sum_of_vals_over_avg = 0.0 for j in range(n_seasons): sum_of_vals_over_avg += self.series[self.slen*j+i]-season_averages[j] seasonals[i] = sum_of_vals_over_avg/n_seasons return seasonals def triple_exponential_smoothing(self): self.result = [] self.Smooth = [] self.Season = [] self.Trend = [] self.PredictedDeviation = [] self.UpperBond = [] self.LowerBond = [] seasonals = self.initial_seasonal_components() for i in range(len(self.series)+self.n_preds): if i == 0: # smooth = self.series[0] trend = self.initial_trend() self.result.append(self.series[0]) self.Smooth.append(smooth) self.Trend.append(trend) self.Season.append(seasonals[i%self.slen]) self.PredictedDeviation.append(0) self.UpperBond.append(self.result[0] + self.scaling_factor * self.PredictedDeviation[0]) self.LowerBond.append(self.result[0] - self.scaling_factor * self.PredictedDeviation[0]) continue if i >= len(self.series): # m = i - len(self.series) + 1 self.result.append((smooth + m*trend) + seasonals[i%self.slen]) # self.PredictedDeviation.append(self.PredictedDeviation[-1]*1.01) else: val = self.series[i] last_smooth, smooth = smooth, self.alpha*(val-seasonals[i%self.slen]) + (1-self.alpha)*(smooth+trend) trend = self.beta * (smooth-last_smooth) + (1-self.beta)*trend seasonals[i%self.slen] = self.gamma*(val-smooth) + (1-self.gamma)*seasonals[i%self.slen] self.result.append(smooth+trend+seasonals[i%self.slen]) # self.PredictedDeviation.append(self.gamma * np.abs(self.series[i] - self.result[i]) + (1-self.gamma)*self.PredictedDeviation[-1]) self.UpperBond.append(self.result[-1] + self.scaling_factor * self.PredictedDeviation[-1]) self.LowerBond.append(self.result[-1] - self.scaling_factor * self.PredictedDeviation[-1]) self.Smooth.append(smooth) self.Trend.append(trend) self.Season.append(seasonals[i % self.slen]) Cross-validation on time series, selection of parameters
Before building a model, let's finally talk about the non-manual estimation of parameters for models.
There is nothing unusual here, as before, you first need to select the appropriate loss function for this task: RMSE , MAE , MAPE , etc., which will monitor the quality of the fit of the model to the source data. Then we will evaluate for cross-validation the value of the loss function for the given model parameters, look for the gradient, change the parameters in accordance with it, and vigorously descend towards the global minimum of error.
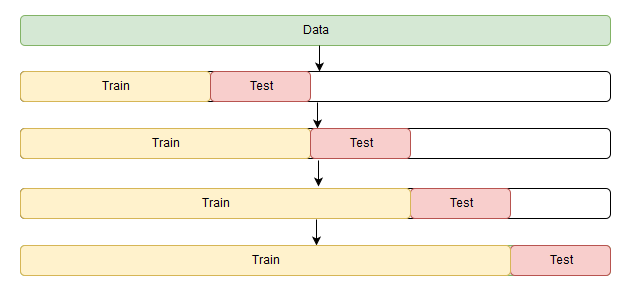
A small snag occurs only in cross-validation. The problem is that the time series has, paradoxically, a temporary structure, and randomly mix in the folds of the values of the entire series without saving this structure is impossible, otherwise in the process all interrelations of observations with each other will be lost. Therefore, we will have to use a slightly more cunning way to optimize the parameters, the official name of which I never found, but on the CrossValidated website, where you can find answers to everything except the main question of Life, the Universe and Everything Else, they suggest the name "cross-validation on rolling basis ", which is not literally translated as cross-validation on a sliding window.
The essence is quite simple - we begin to train the model on a small segment of the time series, from the beginning to some making a forecast for steps forward and consider a mistake. Next, expand the training set to values and predict with before , so we continue to move the test segment of the series until we rest on the last available observation. As a result, we get as many folds as fits in the gap between the original training segment and the entire length of the series.
from sklearn.model_selection import TimeSeriesSplit def timeseriesCVscore(x): # errors = [] values = data.values alpha, beta, gamma = x # - tscv = TimeSeriesSplit(n_splits=3) # , , for train, test in tscv.split(values): model = HoltWinters(series=values[train], slen = 24*7, alpha=alpha, beta=beta, gamma=gamma, n_preds=len(test)) model.triple_exponential_smoothing() predictions = model.result[-len(test):] actual = values[test] error = mean_squared_error(predictions, actual) errors.append(error) # return np.mean(np.array(errors)) The season length value of 24 * 7 was not accidental - the day seasonality is clearly visible in the original row (from here 24), and weekly on weekdays below, on the weekend above, (from here 7), the total seasonal components will turn out 24 * 7.
In the Holt-Winters model, as in the other exponential smoothing models, there is a limit on the amount of smoothing parameters - each of them can take values from 0 to 1, therefore, to minimize the loss function, you need to choose an algorithm that supports restrictions on parameters, in this case - Truncated Newton conjugate gradient.
%%time data = dataset.Users[:-500] # # x = [0, 0, 0] # opt = minimize(timeseriesCVscore, x0=x, method="TNC", bounds = ((0, 1), (0, 1), (0, 1))) # alpha_final, beta_final, gamma_final = opt.x print(alpha_final, beta_final, gamma_final) Out: (0.0066342670643441681, 0.0, 0.046765204289672901) Let's transfer the received optimum values of coefficients , and and build a forecast for 5 days ahead (128 hours)
# , data = dataset.Users model = HoltWinters(data[:-128], slen = 24*7, alpha = alpha_final, beta = beta_final, gamma = gamma_final, n_preds = 128, scaling_factor = 2.56) model.triple_exponential_smoothing() def plotHoltWinters(): Anomalies = np.array([np.NaN]*len(data)) Anomalies[data.values<model.LowerBond] = data.values[data.values<model.LowerBond] plt.figure(figsize=(25, 10)) plt.plot(model.result, label = "Model") plt.plot(model.UpperBond, "r--", alpha=0.5, label = "Up/Low confidence") plt.plot(model.LowerBond, "r--", alpha=0.5) plt.fill_between(x=range(0,len(model.result)), y1=model.UpperBond, y2=model.LowerBond, alpha=0.5, color = "grey") plt.plot(data.values, label = "Actual") plt.plot(Anomalies, "o", markersize=10, label = "Anomalies") plt.axvspan(len(data)-128, len(data), alpha=0.5, color='lightgrey') plt.grid(True) plt.axis('tight') plt.legend(loc="best", fontsize=13); plotHoltWinters() 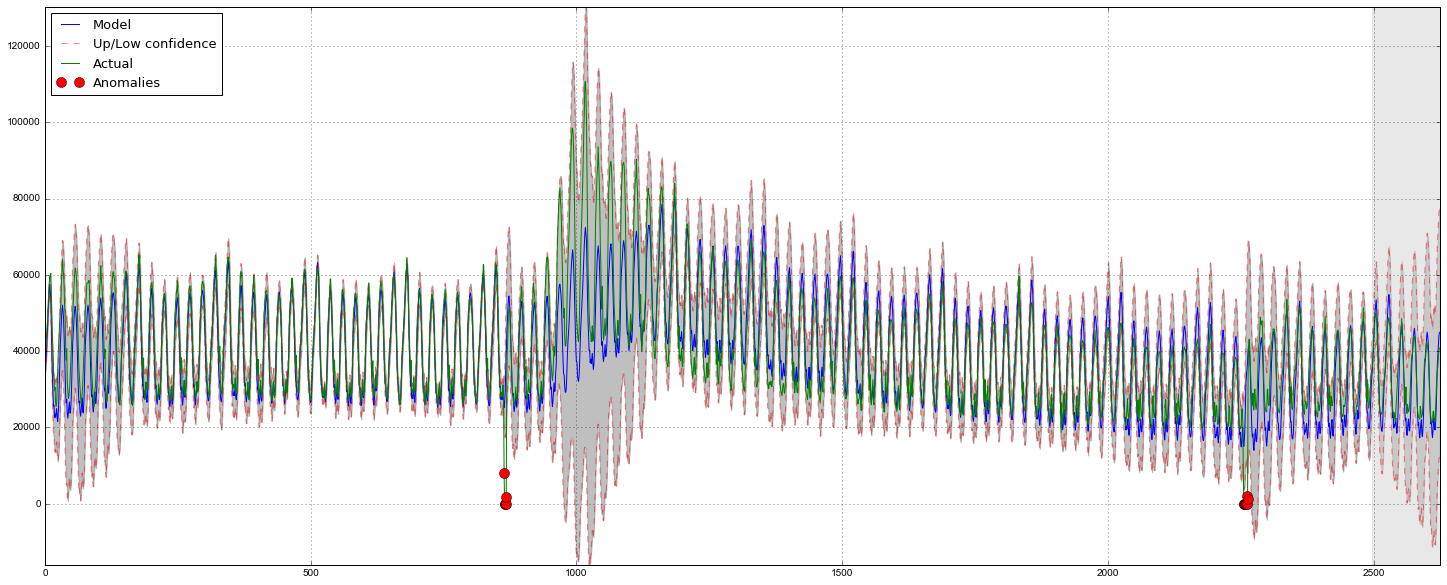
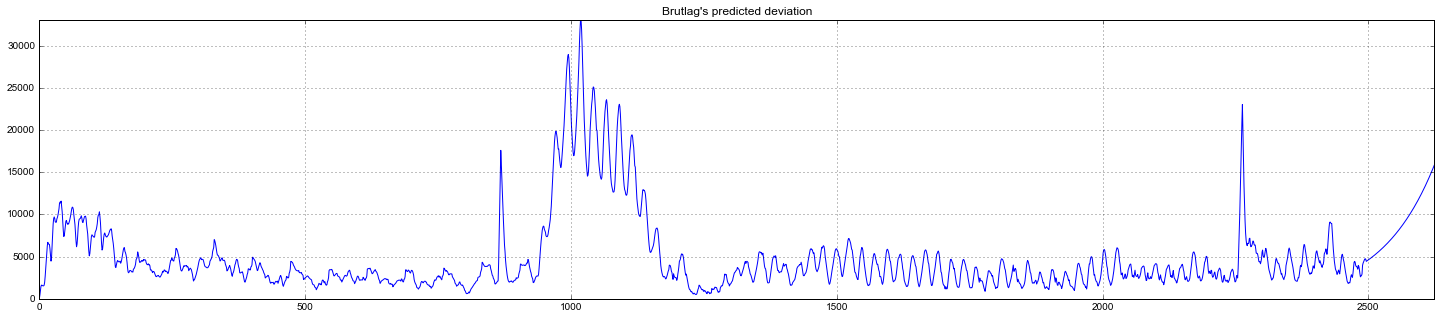
Judging by the schedule, the model described the initial time series quite well, catching weekly and daily seasonality, and even managed to catch anomalous declines that went beyond the confidence intervals. If you look at the simulated deviation, it is clearly seen that the model registers quite sharply for significant changes in the structure of the series, but at the same time quickly returns the variance to normal values, “forgetting” the past. Such a feature makes it possible, quite well and without significant costs for preparing and training the model, to set up a system for detecting anomalies even in fairly noisy rows.
Econometric approach
Stationarity, single roots
Before moving on to modeling, it is worth mentioning such an important property of the time series as stationarity .
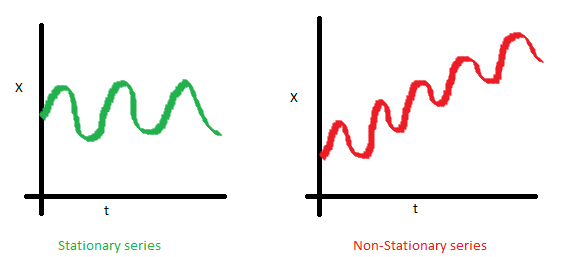
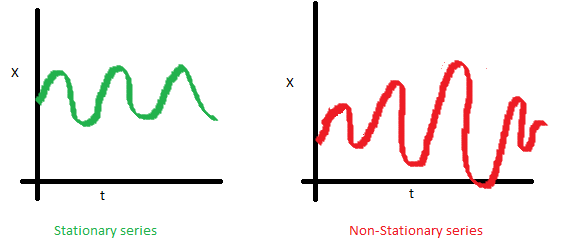
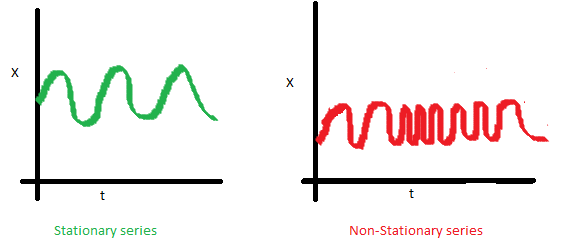
Stationarity is understood as the property of the process not to change its statistical characteristics over time, namely, the constancy of the expectation, the constancy of the dispersion (it is homoscedasticity ) and the independence of the covariance function from time (it should depend only on the distance between observations). You can clearly see these properties in the pictures taken from the post Sean Abu :
- The time series on the right is not stationary, as its expectation increases with time
- There is no luck with dispersion - the spread of the values of the series varies significantly depending on the period
- Finally, the last graph shows that the values of the series suddenly become closer to each other, forming a certain cluster, and as a result we obtain the inconstancy of the covariances
Why is stationarity so important? For the stationary series, it is simple to build a forecast, since we believe that its future statistical characteristics will not differ from the observed current ones. Most time series models somehow model and predict these characteristics (for example, expectation or variance), so in the case of the nonstationarity of the original series, the predictions will turn out to be incorrect. Unfortunately, most of the time series that we have to face outside of the training materials are not stationary, but this can (and should) be dealt with.
To fight nonstationarity, you need to recognize it in person, so let's see how to detect it. To do this, turn to the white noise and random walk to find out how to get from one to another for free and without SMS.
White noise graph:
white_noise = np.random.normal(size=1000) with plt.style.context('bmh'): plt.figure(figsize=(15, 5)) plt.plot(white_noise) 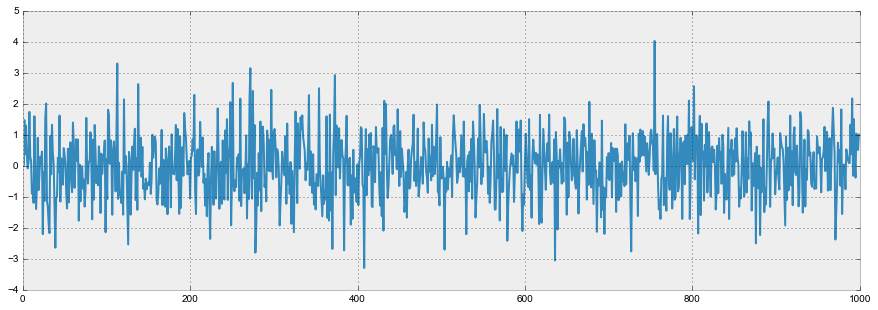
So, the process generated by the standard normal distribution is stationary, oscillates around zero with a deviation of 1. Now, based on it, we will generate a new process in which each subsequent value will depend on the previous one:
def plotProcess(n_samples=1000, rho=0): x = w = np.random.normal(size=n_samples) for t in range(n_samples): x[t] = rho * x[t-1] + w[t] with plt.style.context('bmh'): plt.figure(figsize=(10, 3)) plt.plot(x) plt.title("Rho {}\n Dickey-Fuller p-value: {}".format(rho, round(sm.tsa.stattools.adfuller(x)[1], 3))) for rho in [0, 0.6, 0.9, 1]: plotProcess(rho=rho) 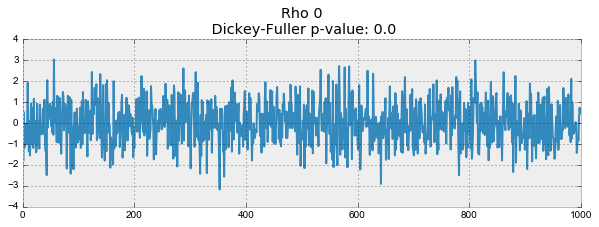
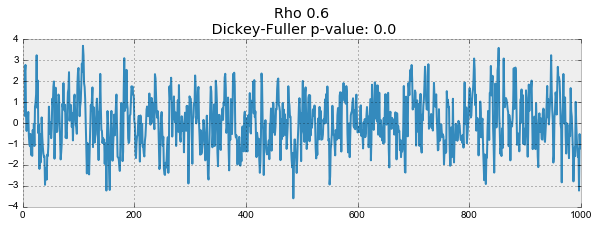
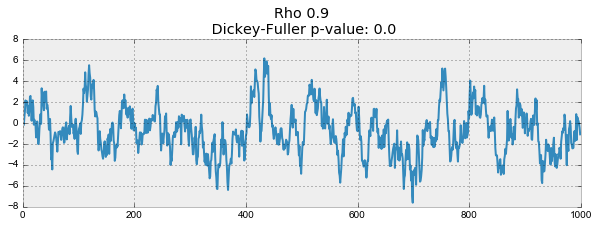
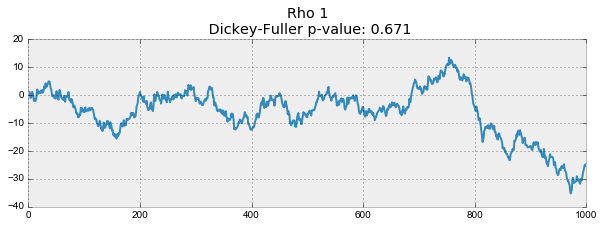
The first graph produced exactly the same stationary white noise that was built earlier. On the second value increased to 0.6, as a result of which wider cycles began to appear on the graph, but on the whole it has not yet ceased to be stationary. The third graph is increasingly deviating from the zero average value, but is still fluctuating around it. Finally, the value — .
- , , . , , — . If a , . - ( ). , . — , , . , , ( ), -, .
— , , , , - .
SARIMA
ARIMA , . — SARIMA Python+R , python , .
def tsplot(y, lags=None, figsize=(12, 7), style='bmh'): if not isinstance(y, pd.Series): y = pd.Series(y) with plt.style.context(style): fig = plt.figure(figsize=figsize) layout = (2, 2) ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2) acf_ax = plt.subplot2grid(layout, (1, 0)) pacf_ax = plt.subplot2grid(layout, (1, 1)) y.plot(ax=ts_ax) ts_ax.set_title('Time Series Analysis Plots') smt.graphics.plot_acf(y, lags=lags, ax=acf_ax, alpha=0.5) smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax, alpha=0.5) print(" -: p=%f" % sm.tsa.stattools.adfuller(y)[1]) plt.tight_layout() return tsplot(dataset.Users, lags=30) Out: -: p=0.190189 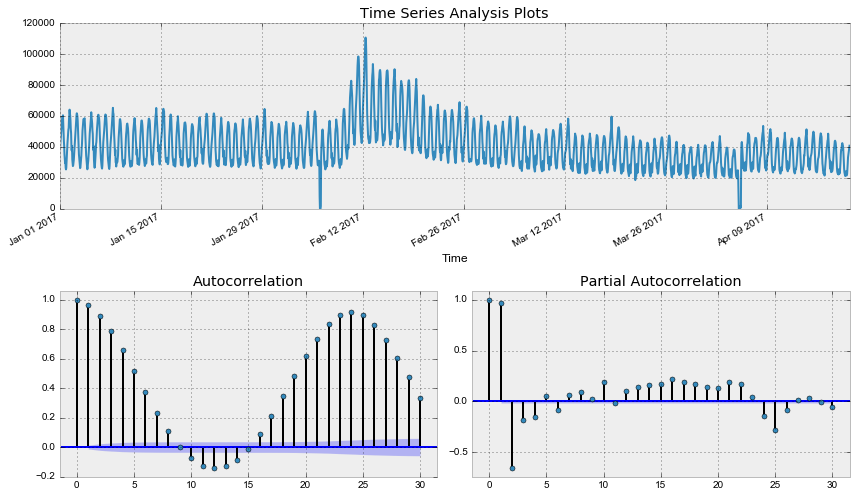
, , - . -.
def invboxcox(y,lmbda): # - if lmbda == 0: return(np.exp(y)) else: return(np.exp(np.log(lmbda*y+1)/lmbda)) data = dataset.copy() data['Users_box'], lmbda = scs.boxcox(data.Users+1) # , tsplot(data.Users_box, lags=30) print(" -: %f" % lmbda) Out: -: p=0.079760 -: 0.587270 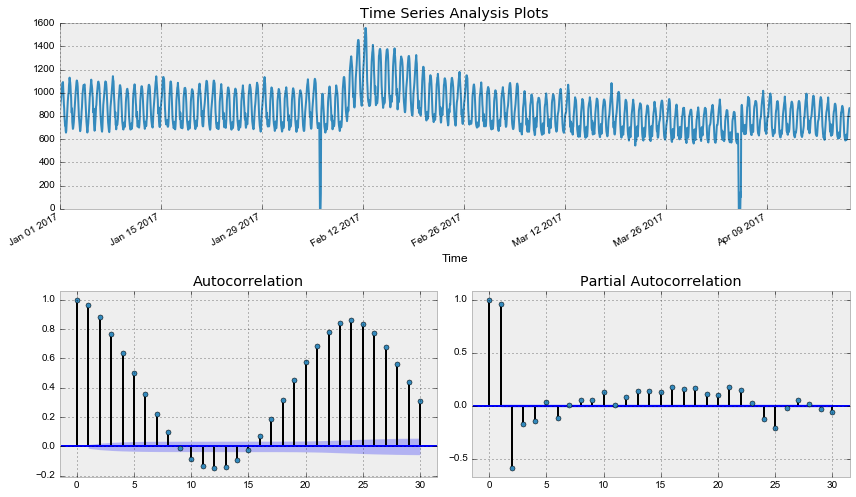
, - - . . :
data['Users_box_season'] = data.Users_box - data.Users_box.shift(24*7) tsplot(data.Users_box_season[24*7:], lags=30) Out: -: p=0.002571 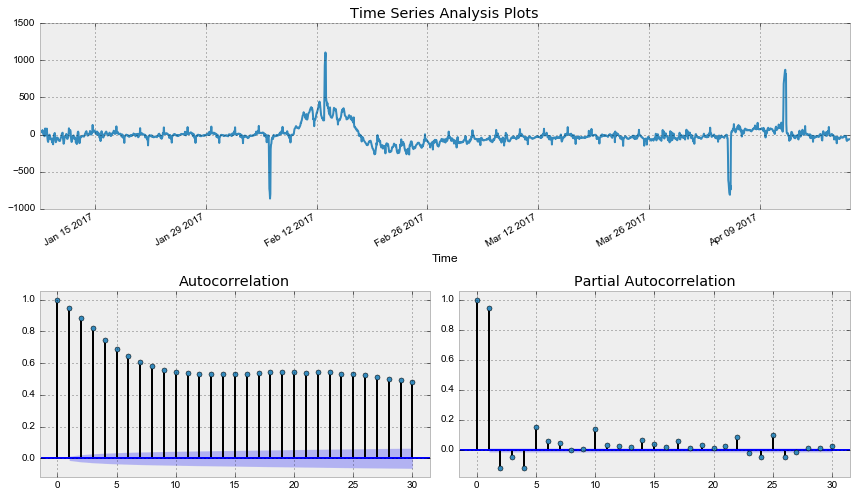
- , - . , , .
data['Users_box_season_diff'] = data.Users_box_season - data.Users_box_season.shift(1) tsplot(data.Users_box_season_diff[24*7+1:], lags=30) Out: -: p=0.000000 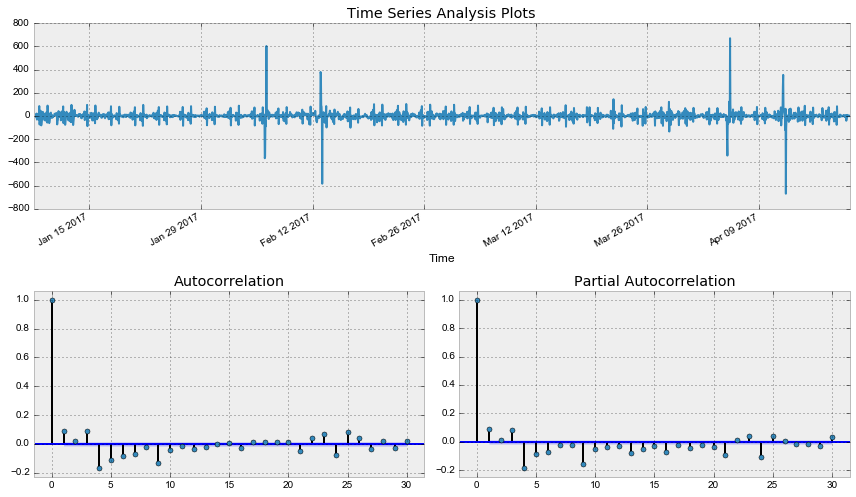
, , SARIMA , , .
Q = 1, P = 4, q = 3, p = 4
ps = range(0, 5) d=1 qs = range(0, 4) Ps = range(0, 5) D=1 Qs = range(0, 1) from itertools import product parameters = product(ps, qs, Ps, Qs) parameters_list = list(parameters) len(parameters_list) Out: 100 %%time results = [] best_aic = float("inf") for param in tqdm(parameters_list): #try except , try: model=sm.tsa.statespace.SARIMAX(data.Users_box, order=(param[0], d, param[1]), seasonal_order=(param[2], D, param[3], 24*7)).fit(disp=-1) # , except ValueError: print('wrong parameters:', param) continue aic = model.aic # , aic, if aic < best_aic: best_model = model best_aic = aic best_param = param results.append([param, model.aic]) warnings.filterwarnings('default') result_table = pd.DataFrame(results) result_table.columns = ['parameters', 'aic'] print(result_table.sort_values(by = 'aic', ascending=True).head()) :
%%time best_model = sm.tsa.statespace.SARIMAX(data.Users_box, order=(4, d, 3), seasonal_order=(4, D, 1, 24)).fit(disp=-1) print(best_model.summary()) Statespace Model Results ========================================================================================== Dep. Variable: Users_box No. Observations: 2625 Model: SARIMAX(4, 1, 3)x(4, 1, 1, 24) Log Likelihood -12547.157 Date: Sun, 23 Apr 2017 AIC 25120.315 Time: 02:06:39 BIC 25196.662 Sample: 0 HQIC 25147.964 - 2625 Covariance Type: opg ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ ar.L1 0.6794 0.108 6.310 0.000 0.468 0.890 ar.L2 -0.0810 0.181 -0.448 0.654 -0.435 0.273 ar.L3 0.3255 0.137 2.371 0.018 0.056 0.595 ar.L4 -0.2154 0.028 -7.693 0.000 -0.270 -0.161 ma.L1 -0.5086 0.106 -4.784 0.000 -0.717 -0.300 ma.L2 -0.0673 0.170 -0.395 0.693 -0.401 0.267 ma.L3 -0.3490 0.117 -2.976 0.003 -0.579 -0.119 ar.S.L24 0.1023 0.012 8.377 0.000 0.078 0.126 ar.S.L48 -0.0686 0.021 -3.219 0.001 -0.110 -0.027 ar.S.L72 0.1971 0.009 21.573 0.000 0.179 0.215 ar.S.L96 -0.1217 0.013 -9.279 0.000 -0.147 -0.096 ma.S.L24 -0.9983 0.045 -22.085 0.000 -1.087 -0.910 sigma2 873.4159 36.206 24.124 0.000 802.454 944.378 =================================================================================== Ljung-Box (Q): 130.47 Jarque-Bera (JB): 1194707.99 Prob(Q): 0.00 Prob(JB): 0.00 Heteroskedasticity (H): 1.40 Skew: 2.65 Prob(H) (two-sided): 0.00 Kurtosis: 107.88 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). :
tsplot(best_model.resid[24:], lags=30) Out: -: p=0.000000 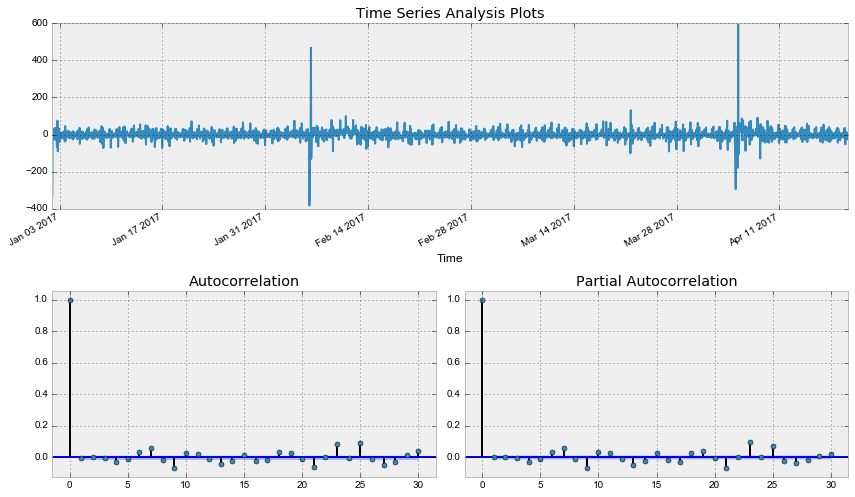
, , ,
data["arima_model"] = invboxcox(best_model.fittedvalues, lmbda) forecast = invboxcox(best_model.predict(start = data.shape[0], end = data.shape[0]+100), lmbda) forecast = data.arima_model.append(forecast).values[-500:] actual = data.Users.values[-400:] plt.figure(figsize=(15, 7)) plt.plot(forecast, color='r', label="model") plt.title("SARIMA model\n Mean absolute error {} users".format(round(mean_absolute_error(data.dropna().Users, data.dropna().arima_model)))) plt.plot(actual, label="actual") plt.legend() plt.axvspan(len(actual), len(forecast), alpha=0.5, color='lightgrey') plt.grid(True) 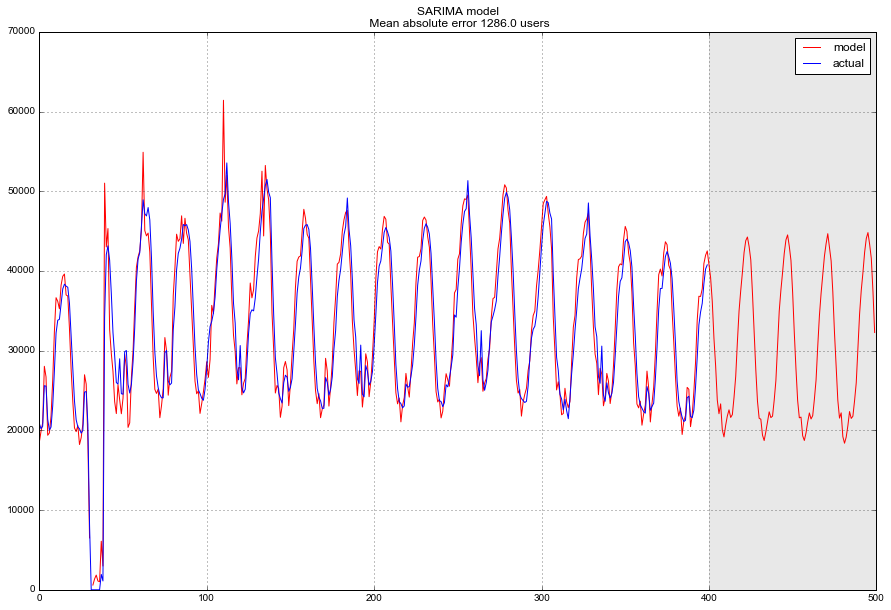
, 1.3 K , , , , .
. , – , , . "-", (, SARIMA), ( – SARIMA), ( SARIMA), . Cheap and angry.
, , , , -, , .
(Feature exctraction)
– . -, , - "0 < 23 ", . – . , . , ( -), .
def code_mean(data, cat_feature, real_feature): """ , cat_feature, - real_feature """ return dict(data.groupby(cat_feature)[real_feature].mean()) , . datetime , hour weekday .
data = pd.DataFrame(dataset) data.columns = ["y"] data.index = data.index.to_datetime() data["hour"] = data.index.hour data["weekday"] = data.index.weekday data['is_weekend'] = data.weekday.isin([5,6])*1 data.head() Out: | y | hour | weekday | is_weekend | |
|---|---|---|---|---|
| Time | ||||
| 2017-01-01 00:00:00 | 34002 | 0 | 6 | one |
| 2017-01-01 01:00:00 | 37947 | one | 6 | one |
| 2017-01-01 02:00:00 | 41517 | 2 | 6 | one |
| 2017-01-01 03:00:00 | 44476 | 3 | 6 | one |
| 2017-01-01 04:00:00 | 46234 | four | 6 | one |
code_mean(data, 'weekday', "y") Out: {0: 38730.143229166664, 1: 38632.828125, 2: 38128.518229166664, 3: 39519.035135135135, 4: 41505.152777777781, 5: 43717.708333333336, 6: 43392.143603133161} , , / , , , , . tsfresh .
, .
def prepareData(data, lag_start=5, lag_end=20, test_size=0.15): data = pd.DataFrame(data.copy()) data.columns = ["y"] # , test_index = int(len(data)*(1-test_size)) # for i in range(lag_start, lag_end): data["lag_{}".format(i)] = data.y.shift(i) data.index = data.index.to_datetime() data["hour"] = data.index.hour data["weekday"] = data.index.weekday data['is_weekend'] = data.weekday.isin([5,6])*1 # , data['weekday_average'] = map(code_mean(data[:test_index], 'weekday', "y").get, data.weekday) data["hour_average"] = map(code_mean(data[:test_index], 'hour', "y").get, data.hour) # data.drop(["hour", "weekday"], axis=1, inplace=True) data = data.dropna() data = data.reset_index(drop=True) # X_train = data.loc[:test_index].drop(["y"], axis=1) y_train = data.loc[:test_index]["y"] X_test = data.loc[test_index:].drop(["y"], axis=1) y_test = data.loc[test_index:]["y"] return X_train, X_test, y_train, y_test vs XGBoost
. , 12 , .
from sklearn.linear_model import LinearRegression X_train, X_test, y_train, y_test = prepareData(dataset.Users, test_size=0.3, lag_start=12, lag_end=48) lr = LinearRegression() lr.fit(X_train, y_train) prediction = lr.predict(X_test) plt.figure(figsize=(15, 7)) plt.plot(prediction, "r", label="prediction") plt.plot(y_test.values, label="actual") plt.legend(loc="best") plt.title("Linear regression\n Mean absolute error {} users".format(round(mean_absolute_error(prediction, y_test)))) plt.grid(True); 
, , , 3K , .
-, , . ( ), Pythonic Cross Validation on Time Series
def performTimeSeriesCV(X_train, y_train, number_folds, model, metrics): print('Size train set: {}'.format(X_train.shape)) k = int(np.floor(float(X_train.shape[0]) / number_folds)) print('Size of each fold: {}'.format(k)) errors = np.zeros(number_folds-1) # loop from the first 2 folds to the total number of folds for i in range(2, number_folds + 1): print('') split = float(i-1)/i print('Splitting the first ' + str(i) + ' chunks at ' + str(i-1) + '/' + str(i) ) X = X_train[:(k*i)] y = y_train[:(k*i)] print('Size of train + test: {}'.format(X.shape)) # the size of the dataframe is going to be k*i index = int(np.floor(X.shape[0] * split)) # folds used to train the model X_trainFolds = X[:index] y_trainFolds = y[:index] # fold used to test the model X_testFold = X[(index + 1):] y_testFold = y[(index + 1):] model.fit(X_trainFolds, y_trainFolds) errors[i-2] = metrics(model.predict(X_testFold), y_testFold) # the function returns the mean of the errors on the n-1 folds return errors.mean() %%time performTimeSeriesCV(X_train, y_train, 5, lr, mean_absolute_error) Size train set: (1838, 39) Size of each fold: 367 Splitting the first 2 chunks at 1/2 Size of train + test: (734, 39) Splitting the first 3 chunks at 2/3 Size of train + test: (1101, 39) Splitting the first 4 chunks at 3/4 Size of train + test: (1468, 39) Splitting the first 5 chunks at 4/5 Size of train + test: (1835, 39) CPU times: user 59.5 ms, sys: 7.02 ms, total: 66.5 ms Wall time: 18.9 ms Out: 4613.17893150896 5 4.6 K , , .
XGBoost...

import xgboost as xgb def XGB_forecast(data, lag_start=5, lag_end=20, test_size=0.15, scale=1.96): # X_train, X_test, y_train, y_test = prepareData(dataset.Users, lag_start, lag_end, test_size) dtrain = xgb.DMatrix(X_train, label=y_train) dtest = xgb.DMatrix(X_test) # params = { 'objective': 'reg:linear', 'booster':'gblinear' } trees = 1000 # - rmse cv = xgb.cv(params, dtrain, metrics = ('rmse'), verbose_eval=False, nfold=10, show_stdv=False, num_boost_round=trees) # xgboost , - bst = xgb.train(params, dtrain, num_boost_round=cv['test-rmse-mean'].argmin()) # #cv.plot(y=['test-mae-mean', 'train-mae-mean']) # - deviation = cv.loc[cv['test-rmse-mean'].argmin()]["test-rmse-mean"] # , prediction_train = bst.predict(dtrain) plt.figure(figsize=(15, 5)) plt.plot(prediction_train) plt.plot(y_train) plt.axis('tight') plt.grid(True) # prediction_test = bst.predict(dtest) lower = prediction_test-scale*deviation upper = prediction_test+scale*deviation Anomalies = np.array([np.NaN]*len(y_test)) Anomalies[y_test<lower] = y_test[y_test<lower] plt.figure(figsize=(15, 5)) plt.plot(prediction_test, label="prediction") plt.plot(lower, "r--", label="upper bond / lower bond") plt.plot(upper, "r--") plt.plot(list(y_test), label="y_test") plt.plot(Anomalies, "ro", markersize=10) plt.legend(loc="best") plt.axis('tight') plt.title("XGBoost Mean absolute error {} users".format(round(mean_absolute_error(prediction_test, y_test)))) plt.grid(True) plt.legend() XGB_forecast(dataset, test_size=0.2, lag_start=5, lag_end=30) 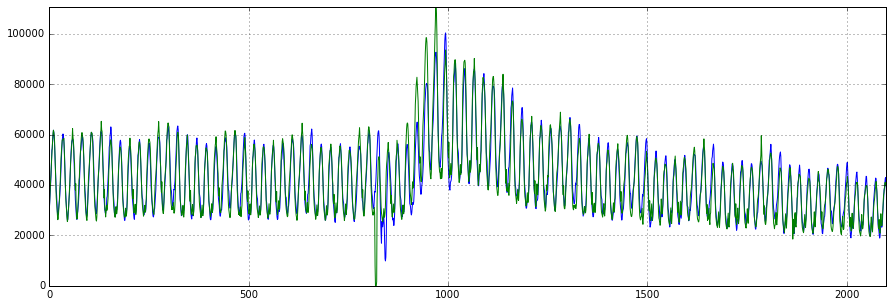

3 K , . , , , , , , ..
Conclusion
. , , . , 60- , ( 19-), - LSTM RNN. , , , — . , - . . SARIMA- , , 10 , - .
Actual homework is announced during the regular session of the course, you can follow in the VC group and in the repository of the course.
- wiki- "Machine Learning". - , .
Useful resources
- Open Machine Learning Course. Topic 9. Part 1. Time series analysis in Python
- Video recording of the lecture based on this article.
- Open Machine Learning Course. Topic 9. Part 2. Predicting the future with Facebook Prophet
- - Duke — , ARIMA
- Comparison of ARIMA and Random Forest time series models for prediction of avian influenza H5N1 outbreaks — ,
- Time Series Analysis (TSA) in Python — Linear Models to GARCH ARIMA (Brian Christopher)
GitHub-
Jupyter.
')
Source: https://habr.com/ru/post/327242/
All Articles