Introduction

Quite often, especially in the use of engineering disciplines, the term “slowing down” is used, that is, acceleration, the action of which leads to a decrease in the velocity modulus. At the same time, a certain negative sign is attributed to such acceleration, which underlines this most delaying effect.

In my humble opinion, this concept is not only redundant, but also harmful from a methodological point of view. It throws a kind of muddy veil on the essence of the quantities describing the mechanical motion.

In fact, to describe the same braking of a car or a parachutist, it is not necessary to attribute an acceleration sign, it is enough to understand that acceleration is a vector value and the ability to correctly move from operations with vectors to operations with their projections on the axes of the selected coordinate system.
')
The article aims to debunk the need to use the term "slowing down" in solving practical problems of mechanics, and if the reader is not embarrassed by another lecture on theoretical theory, welcome to Cat.

1. The concept of the derivative of the vector in time

Consider a vector such that


that is, the modulus and direction of this vector are time dependent. Calculate the change in the change of this vector over a period of time.


Now, using the fact that for the vectors the multiplication operation is defined by a number, multiply (1) by the reciprocal of the time increment . Due to the fact that we get a vector directed in the same direction as vector (1) (see Figure 1)

Fig. 1. The geometric meaning of the time vector derivative


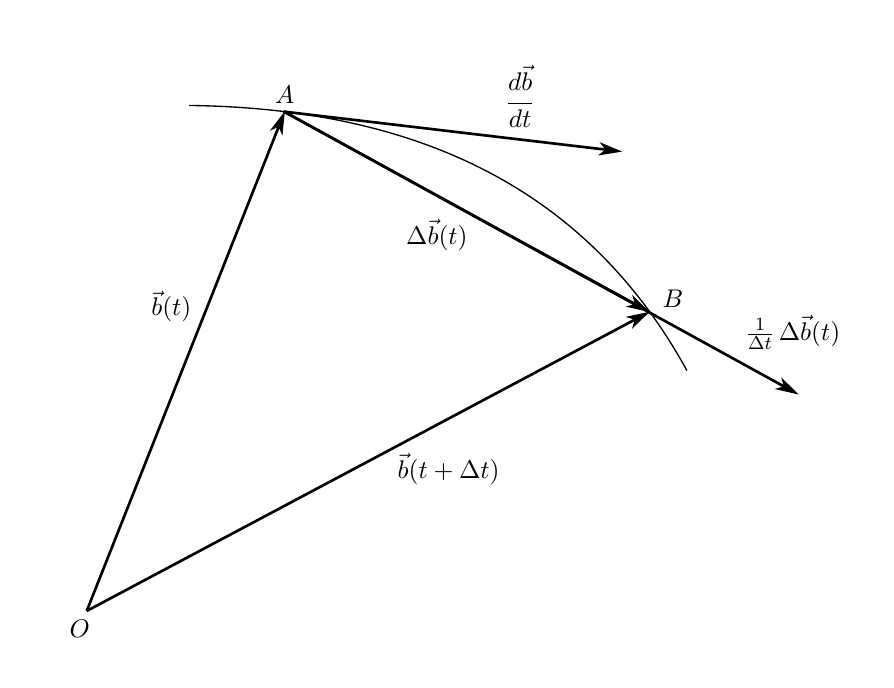
We now turn to the limit at


The relation (2) is the limit of the ratio of the increment of the vector function to the increment of its argument and is called the derivative of the vector with respect to time . As can be seen from our calculations, the time derivative of a vector is also a vector. How is this vector directed?

Let's talk, looking at the geometric interpretation in Figure 1. Vector occupies the secant position with respect to the trajectory that the end of the vector describes for a period of time . This trajectory is called the hodograph of the vector function. . The secant intersects the locus at points A and B. When aspiring to zero, point A remains fixed, and point B shifts towards point A. In the limit, the secant takes a position tangent to the hodograph at point A.

That is, you can enter the following definition

Derivative of vector there is a time vector directed tangent to the hodograph of the vector

Thus, the derivative of the vector shows how the modulus and the direction of the vector change. About any "sign" of the derivative there is no question here in principle. And it cannot go - the derivative of a vector with respect to time is also a vector, and for a vector there is no concept of a sign.

2. Derivative of a constant vector modulo

Assume now that our vector has a constant length, that is


and only its direction in space changes. Will this vector have a nonzero derivative? Of course it will be! Multiply the vector scalar by itself


Differentiate (3) by time


Derivative of vector module equal to zero, because the module does not change in time. Then, using the rule of differentiation of the product, we open the left part (4)


using the commutativity property of a scalar product, we obtain


or


That is, the scalar product of a vector by its own derivative is zero, which means


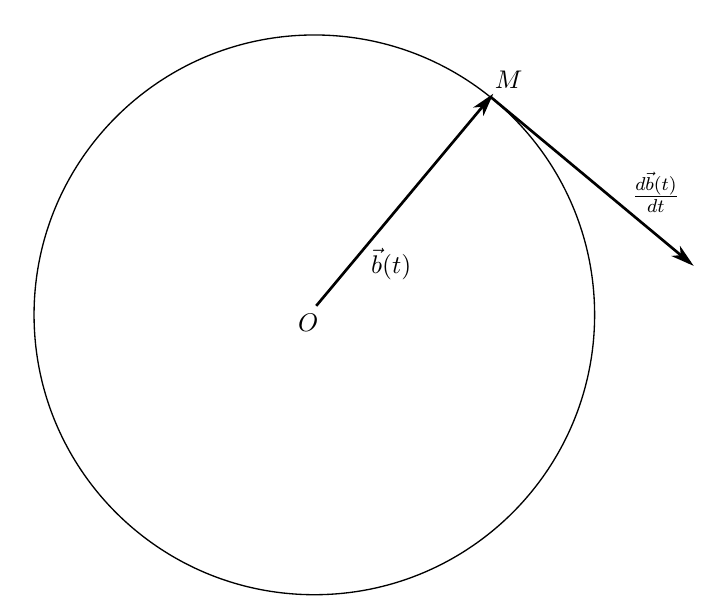
Thus, the derivative of a vector with a constant length is not only non-zero, but it is a vector perpendicular to the original one. The locus of such a vector will be a circle with a radius equal to the length of the vector (Figure 2).

We are faced with a situation where we calculate the acceleration of a point moving uniformly along a circle. She has a centripetal acceleration perpendicular to the velocity vector.

The derivative of the vector will be equal to zero only if the vector does not change either the module or the direction.

Fig 2. Vector with constant length, its hodograph and derivative

3. Speed ​​and acceleration

Now, on the basis of the foregoing, we give the definition of the velocity of a material point. Let the position of a point in space be characterized by a vector called the radius vector of a point (see Figure 3). Then

Point velocity vector called the first derivative of the radius vector of a point in time

The velocity vector of a point is directed tangentially to its trajectory.

That's right - the trajectory is the hodograph of the radius vector, and the choice of origin O from which we release the radius vector does not matter.

Fig. 3. The vectors of the velocity and acceleration of the material point


The concept of acceleration is introduced in a similar way.

Point acceleration vector there is the first derivative of the velocity vector of a point in time

The acceleration vector is directed tangentially to the velocity vector hodograph.

The geometrical illustration of these definitions is shown in Figure 3. When a point moves in a circle with a constant velocity along the module, the acceleration is directed exactly to the center of this circle (Figure 4)



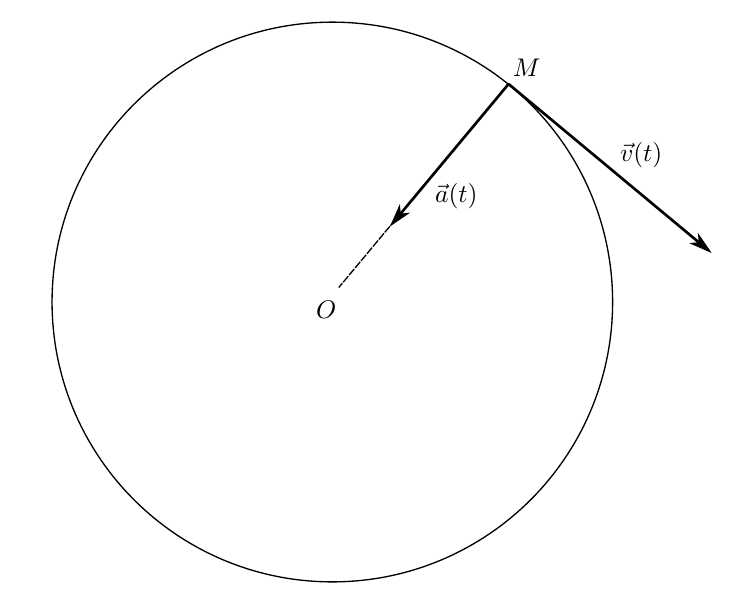
in full accordance with the definition of the derivative of the vector constant in magnitude. In this case, the acceleration vector just shows how the direction of the velocity vector changes.

Conclusion or where does the sign come from

Solving the problem of mechanics, we inevitably move from vector equations to equations in projections on the axes of the selected coordinate system. And, if the acceleration vector is directed against the velocity vector, then the sign of its projection is different from the sign of the velocity vector projection. And the latter can be negative, and the acceleration projection is positive, it all depends on the chosen coordinate system! . It is in this situation that the term “slowdown” is used in engineering practice.

However, the sign of the projection and its naming does not have any relation to mechanics; they already refer to the formal procedure of calculations when solving a problem and do not carry a mechanical meaning. So the concept of “slowing down” is the result of a free interpretation of intermediate results of calculations.

Thank you for your attention!