Cooking Physically Based Rendering + Image-based Lighting. Theory + practice. Step by step
 Hey, hello. 2017 is in the yard. Even unpretentious mobile and browser applications are beginning to slowly draw physically correct lighting. The Internet is replete with a bunch of articles and ready-made shaders. And it seems that it should be so easy to smear PBR too ... Or not?
Hey, hello. 2017 is in the yard. Even unpretentious mobile and browser applications are beginning to slowly draw physically correct lighting. The Internet is replete with a bunch of articles and ready-made shaders. And it seems that it should be so easy to smear PBR too ... Or not?In reality, honest PBR is difficult to do, because it is easy to achieve a similar result, but it is difficult to achieve the right result. And the Internet is full of articles that do exactly the same result, instead of the correct one. Separating flies from cutlets in this chaos becomes difficult.
Therefore, the purpose of the article is not only to understand what PBR is and how it works, but also to learn how to write it. How to debug, where to look, and what errors can typically be made.
The article is intended for people who already know hlsl and are quite familiar with linear algebra, and you can write your simplest nonPBR Phong light. In general, I will try to explain as simply as possible, but I hope that you already have some experience with shaders.
The examples will be written in Delphi (and compiled under FreePascal), but the main code will still be in hlsl. Therefore, do not be afraid if you do not know Delphi.
Where can I see and touch?
To build the examples, you'll need the AvalancheProject code. This is my DX11 / OpenGL framework. You will also need the Vampyre Imaging Library . This is a library for working with pictures, I use it to load textures. The source code for the examples is here . For those who do not want / can not collect binaries, and wants to use the already collected, then they are here .
So we fastened the seat belts, let's go.
')
1 Importance of sRGB support
Our monitors usually show an sRGB image. This is 95% true for desktops, and to some extent true for laptops (and on phones there is total arbitrariness).
This is due to the fact that our perception is not linear, and we notice small changes in light in dark areas better than the same absolute changes in light areas. If it is rough, then when you increase the brightness by 4 times, we perceive it as an increase in brightness by 2 times. I prepared you a picture:

Before trying to understand the picture - make sure that your browser or operating system has not resized the image.
In the middle of the square, consisting of horizontal single-pixel black and white stripes. The amount of light from this square is exactly 2 times less than from pure white. Now, if you move away from the screen so that the stripes merge into a square of the same color, then on the calibrated monitor the central square should merge with the right square, and the left one will be much darker. If you now take the color of the left square with a pipette, you will find that it is 128, and the right one - 187. It turns out that when mixing 50/50 black: 0 0 0 and white 255 255 255 we get not ~ 128 128 128, but already 187 187 187.
Therefore, for a physically correct render, it is important for us that the white multiplied by 0.5 on the screen becomes 187 187 187. For this, the graphic API (DirectX and OpenGL) has hardware support for sRGB. When working with textures in the shader, they are transferred to the linear space, and when displayed on the screen they are transferred back to sRGB.
I will not dwell on how to achieve this in DirectX / OpenGL. This is easy to google. And make sure that your sRGB is working quite simply. The linear gradient from black to white should change something like this:

I just needed to show the importance of working in linear space, because this is one of the first mistakes that is found on the Internet in articles about PBR.
2 Cook-Torrance
A physically correct render usually takes into account such things as:
- Fresnel Reflection Ratios
- Law of energy conservation
- Microfacet theory for reflected light and reradiated
The list can be extended to microfacet theory for subsurface scattering and physically correct refraction, etc., but in the context of this article we will talk about the first three points.
2.1 Microfacet Theory
The surfaces of various materials in the real world are not absolutely smooth, but very rough. These irregularities are much longer than the light wavelength, and make a significant contribution to the illumination. It is impossible to describe a rough plane with one normal vector, and the normal usually describes a certain average value of the macro-surface:
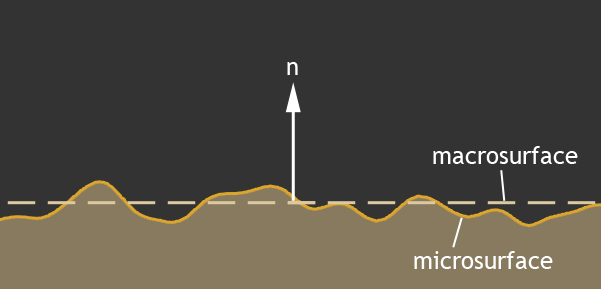
When in fact the main contribution to the reflected light is made precisely by micro-borders:
We all remember that the angle of incidence is equal to the angle of reflection, and the vector h in this figure describes precisely the normal of the micrograin, which contributes to the illumination. It is the light from this point of the surface that we will see.
In addition, part of the world does not physically reach the microfaces that could reflect it:
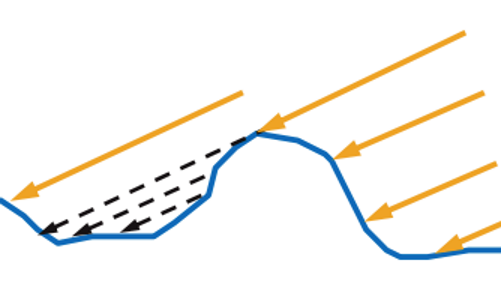
This is called self shadowing, or self shadowing .
And the light that has reached the surface and reflected is not always able to fly out:
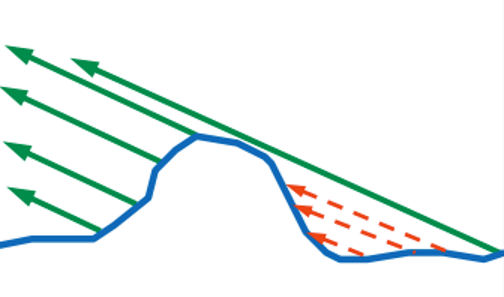
This is called self-overlap, or masking . And the most cunning light can be reflected two or more times:

And this effect is called retroreflection . All these micrograins are described by a roughness coefficient ( roughness ), which usually (but not always) lies in the range (0; 1). At 0, we have a perfectly smooth surface and no micrograins. At 1, micrograins are distributed so that they reflect light in a hemisphere . Sometimes the coefficient of roughness is replaced by the coefficient of smoothness, which is equal to 1-roughness.
That's basically all how surfaces behave for reflected light.
2.2 Bidirectional Reflectance Distribution Function
So, light reaching the surface is partially reflected, and partially penetrates into the material. Therefore, from the total flow of light, first isolate the amount of reflected light. Moreover, we are interested not only in the amount of reflected light, but also in the amount of light that enters our eyes. And this is described by various Bidirectional Reflectance Distribution Function (BRDF) .
We will consider one of the most popular models - the Cook-Torrance model:

In this function:
V - vector from the surface into the eye of the observer
N - macro-normal surface
L - direction from the surface to the light source
D is the distribution function of the reflected light taking into account the microfaces. Describes the number of microfaces turned to us so as to reflect light into our eyes.
G is the distribution function of self-shadowing and self-overlapping. Unfortunately, the light re-reflected several times in this function is not taken into account, and will be lost. We will return to this point later in the article.
F - Fresnel reflection coefficients. Not all light is reflected. Part of the light is refracted and falls inside the material. In this function, F describes the amount of reflected light.
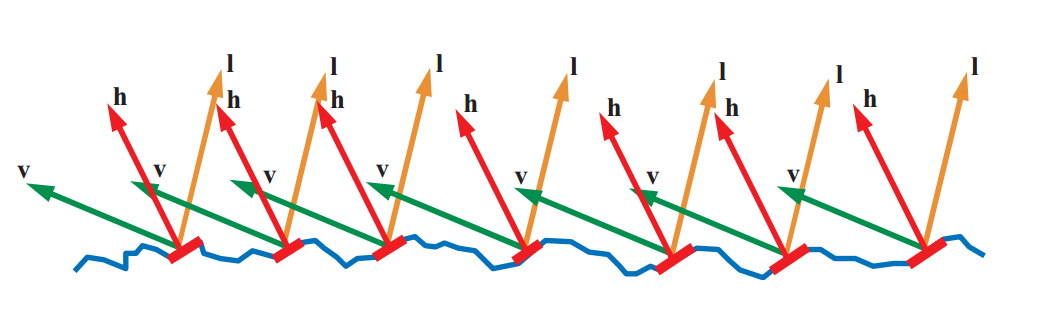
Even in the formula one cannot see such a parameter as the H vector, but it will be actively used in the D and G distribution functions. The meaning of the H vector is to describe the normal microfaces that contribute to the reflected light. Those. a beam of light caught on a micro-facet with a normal H will always be reflected in our eyes. Since the angle of incidence is equal to the angle of reflection, we can always calculate H as normalize (V + L) . Something like that:
The distribution functions D and G are an approximate solution, and there are many and different ones. At the end of the article I will leave a reference to the list of such distributions. We will use the GGX distribution functions developed by Bruce Walter.
2.3 G. Overlap geometry
Let's start with self-shadowing and overlapping. This is a function of G. The GGX distribution of this function uses the Smith method (Smith 1967, "Geometrical shadowing of a random rough surface"). The main point of this method is that the amount of lost light from the light to the surface and from the surface to the observer will be symmetrical with respect to the macro-normal surface. Therefore, we can divide the function G into 2 parts, and calculate the first half of the lost light from the angle between N and L , and then using the same function, calculate the lost light from the angle between V and N. Here is one half of such a function G and describes the distribution of GGX :
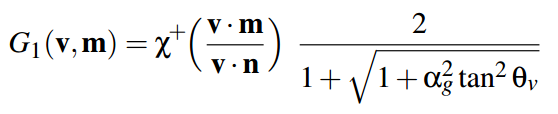
In this function
α g is the square of the surface roughness (roughness * roughness).
θ v is the angle between the macronormal of N and in one case the light L , in the other case the vector on the observer V.
Χ is a function that returns zero if the checked beam comes from the opposite side of the normal, otherwise it returns one. In the HLSL shader, we will remove this from the formula, since We will check at the earliest stages, and do not illuminate such a pixel at all. In the original formula, we have a tangent, but for the render it is convenient to use the cosine of the angle, since we get it through the scalar product. Therefore, I slightly transformed the formula and wrote it in HLSL code:
float GGX_PartialGeometry(float cosThetaN, float alpha) { float cosTheta_sqr = saturate(cosThetaN*cosThetaN); float tan2 = ( 1 - cosTheta_sqr ) / cosTheta_sqr; float GP = 2 / ( 1 + sqrt( 1 + alpha * alpha * tan2 ) ); return GP; } And we consider the total G from the light vector and the observer vector as:
float roug_sqr = roughness*roughness; float G = GGX_PartialGeometry(dot(N,V), roug_sqr) * GGX_PartialGeometry(dot(N,L), roug_sqr); If we render the balls and output this G , we get something like this:

The light source is on the left. The roughness of the balls from left to right is from 0.05 to 1.0.
Check : No pixel should be greater than one. Put this condition here:
Out.Color = G; if (Out.Color.r > 1.000001) Out.Color.gb = 0.0; If at least one output pixel is greater than one, then it will turn red. If everything is done correctly, all pixels will remain white.
2.4 D. Distribution of reflective microfaces
So we have the following parameters: macronormal , roughness , and H vector. From these parameters, it is possible to establish which% of the microfaces on a given pixel have a normal coinciding with H. In GGX , this function is responsible for this:
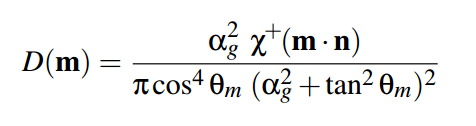
Χ is the same function as in the case of G. We throw it away for the same reasons.
α g - the square of the surface roughness
θ m is the angle between the macronormal of N and our H vector.
I made some small transformations again, and replaced the tangent by the cosine of the angle. As a result, we have the following HLSL function:
float GGX_Distribution(float cosThetaNH, float alpha) { float alpha2 = alpha * alpha; float NH_sqr = saturate(cosThetaNH * cosThetaNH); float den = NH_sqr * alpha2 + (1.0 - NH_sqr); return alpha2 / ( PI * den * den ); } And call it like this:
float D = GGX_Distribution(dot(N,H), roughness*roughness); If we display the value D on the screen, we get something like this:

The roughness still varies from 0.05 on the left, to 1.0 on the right.
Check : Pay attention to the fact that with a roughness of 1.0 all the light should be distributed evenly throughout the hemisphere. This means that the last ball must be monotonous. Its color should be 153,153,153 (+ -1 due to rounding), which, when transferred from sRGB to linear space, will yield 0.318546778125092. By multiplying this number by PI, we should get approximately one, which corresponds to the reflection on the hemisphere. Why PI? Because the integral cos (x) sin (x) over the hemisphere gives PI.
2.5 F. Fresnel Reflection Ratios
A beam of light hitting the border of two different environments is reflected and refracted.
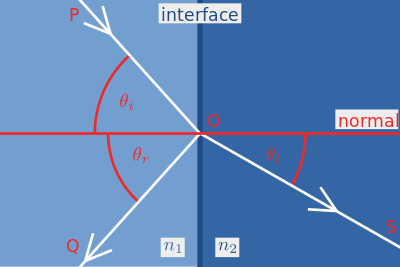
Fresnel formulas fairly accurately describe the laws by which this happens, but if you go to the wiki and look at these multi-story formulas, you will see that they are heavy. Fortunately, there is a good approximation, which is used in most cases in PBR renders, it is Schlick approximation :

Where R0 is calculated as the ratio of the refractive indices:
and cos θ in the formula is the cosine of the angle between the incident light and the normal. It can be seen that for cosθ = 1, the formula degenerates into R0 , and this means that the physical meaning of R0 is the amount of reflected light if the beam falls perpendicular to the surface. Let's arrange this immediately in the hlsl code:
float3 FresnelSchlick(float3 F0, float cosTheta) { return F0 + (1.0 - F0) * pow(1.0 - saturate(cosTheta), 5.0); } Note that F0 is of type float3 . This is due to the fact that the reflection coefficients may be different for different channels. Different materials reflect different amounts of light depending on the wavelength:
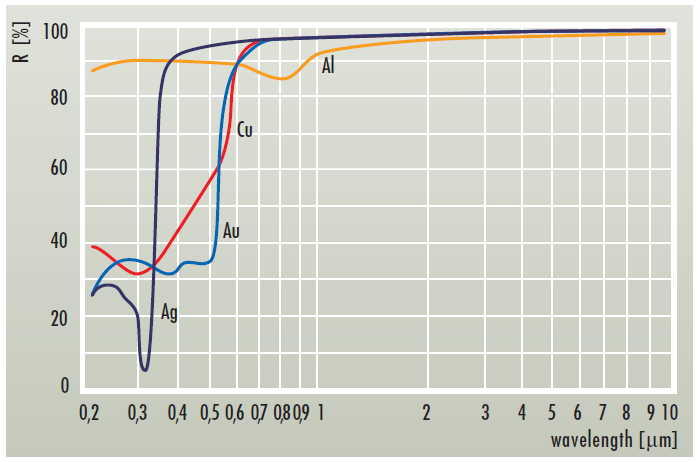
And since in our eyes RGB cones, then float3 will be enough for people.
2.6 We put together
Well. Let's now assemble our function that returns the reflected color entirely:
float3 CookTorrance_GGX(float3 n, float3 l, float3 v, Material_pbr m) { n = normalize(n); v = normalize(v); l = normalize(l); float3 h = normalize(v+l); //precompute dots float NL = dot(n, l); if (NL <= 0.0) return 0.0; float NV = dot(n, v); if (NV <= 0.0) return 0.0; float NH = dot(n, h); float HV = dot(h, v); //precompute roughness square float roug_sqr = m.roughness*m.roughness; //calc coefficients float G = GGX_PartialGeometry(NV, roug_sqr) * GGX_PartialGeometry(NL, roug_sqr); float D = GGX_Distribution(NH, roug_sqr); float3 F = FresnelSchlick(m.f0, HV); //mix float3 specK = G*D*F*0.25/NV; return max(0.0, specK); } At the very beginning, we filter the light that does not hit the surface:
if (NL <= 0.0) return 0.0; as well as areas that we do not see: if (NV <= 0.0) return 0.0; prepare different scalar products, and feed them with our functions GGX_PartialGeometry () , GGX_Distribution () , FresnelSchlick () . Next, multiply everything according to the formula already mentioned:
Please note that I did not divide into NL:
float3 specK = G*D*F*0.25/NV; because then we still multiply by NL , and NL is reduced. At the exit, I got this picture:
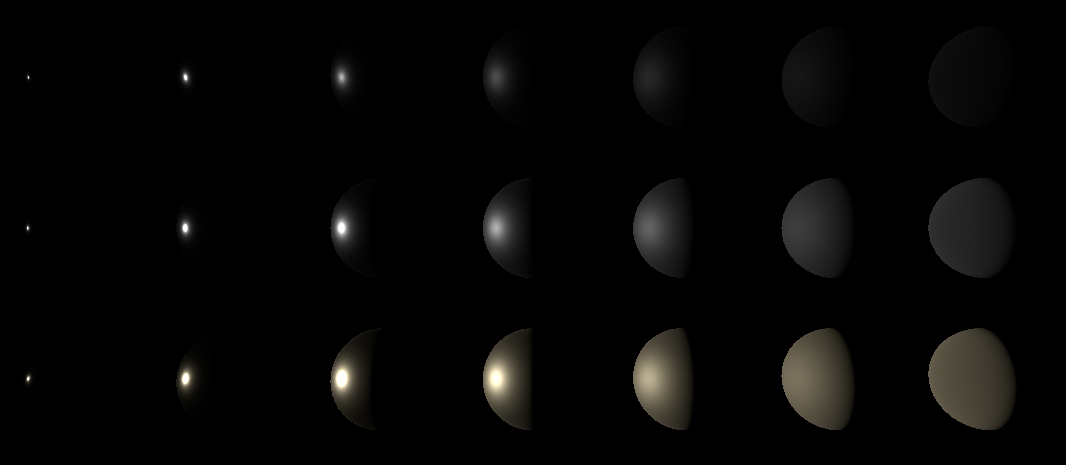
From left to right, the roughness increases from 0.05 to 1.0
From top to bottom, the different Fresnel F0 coefficients are:
1. (0.04, 0.04, 0.04)
2. (0.24, 0.24, 0.24)
3. (1.0, 0.86, 0.56)
2.7 Lambertian diffused light model
So the FresnelSchlick function will return us the amount of reflected light. The rest of the light will be 1.0-FresnelSchlick () .
Here I want to make a retreat.
Many consider this unit minus Fresnel differently. For example, in UE4, FresnelSchlick is counted from dot (V, H). Somewhere take two coefficients (from dot (L, N) and dot (V, N)). As for me - it is more logical to take from dot (L, N). Now I can say that I do not know exactly how correct, and how will be closer to reality. When I study this question, I will fill this gap in the article, but for now we will do it as in UE4, that is, dot (V, H).
This light will pass through the surface and will randomly wander inside it until it is absorbed / reemitted / leaves the surface at another point. Since we are not yet affecting the subsurface scattering, then roughly assume that this light will be absorbed or reemitted in a hemisphere:
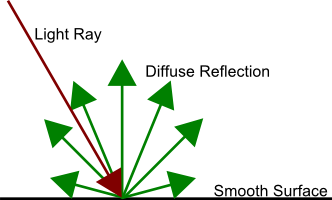
In the first approximation, it will suit us. This dispersion is described by the Lambert lighting model. This is described by the simplest formula LightColor * dot (N, L) / PI . That is, everyone is familiar with dot (N, L) , which describes the density of the light flux reaching the surface, and the division by PI with which we have already met in the form of an integral hemisphere . The amount of light absorbed / reradiated describes the float3 parameter, which is called albedo . It's all very similar with the F0 parameter. The subject re-radiates only certain wavelengths.
Since there is nothing more to say about the Lambert lighting model, then we add it to our CookTorrance_GGX (although it might have been more correct to put it into a separate function, but I am too lazy to pull out the F parameter):
float3 specK = G*D*F*0.25/(NV+0.001); float3 diffK = saturate(1.0-F); return max(0.0, m.albedo*diffK*NL/PI + specK); But in general, the function has become such
float3 CookTorrance_GGX(float3 n, float3 l, float3 v, Material_pbr m) { n = normalize(n); v = normalize(v); l = normalize(l); float3 h = normalize(v+l); //precompute dots float NL = dot(n, l); if (NL <= 0.0) return 0.0; float NV = dot(n, v); if (NV <= 0.0) return 0.0; float NH = dot(n, h); float HV = dot(h, v); //precompute roughness square float roug_sqr = m.roughness*m.roughness; //calc coefficients float G = GGX_PartialGeometry(NV, roug_sqr) * GGX_PartialGeometry(NL, roug_sqr); float D = GGX_Distribution(NH, roug_sqr); float3 F = FresnelSchlick(m.f0, HV); //mix float3 specK = G*D*F*0.25/(NV+0.001); float3 diffK = saturate(1.0-F); return max(0.0, m.albedo*diffK*NL/PI + specK); } Here is what I did after adding the diffuse component:

Albedo of three materials (in linear space) from top to bottom:
1. (0.47, 0.78, 0.73)
2. (0.86, 0.176, 0)
3. (0.01, 0.01, 0.01)
Well, here I put the second light source on the right, and increased the intensity of the sources 3 times:

The current example can be downloaded here in the repository. I also remind you that the collected versions of the examples here .
3.0 Image based lighting

We have now examined how a point source of light contributes to the illumination of each pixel of an image. Of course, we neglected the fact that the source should decay from the square of the distance, as well as the fact that the source cannot be a point source, and we could take all this into account, but let's look at another approach to lighting. The fact is that all the objects around reflect / reradiate light, and thereby illuminate the environment. You come to the mirror and see yourself. The reflected light in the mirror was re-emitted / reflected by your body not so long ago, and that is why you see yourself in it. If we want to receive beautiful reflections in smooth objects, then we will need to count for each pixel the light from the hemisphere surrounding this pixel. In games use in this case such fake. Prepare a large texture with the environment (in fact, a 360 ° photo or a cubic map). Each pixel of such a photo is a small emitter. Next, with the help of “some magic”, pixels are selected from such textures, and the pixel is drawn with the code that we wrote above for point sources. That is why the technique is called Image based lighting (ie, the texture of the environment is used as a source of light).
3.1 Monte-Carlo
Let's start with the simple. Use the Monte Carlo method to calculate our coverage. For those who are afraid and do not understand the terrible words "Monte Carlo method" I will try to explain on the fingers. All points in the map affect the lighting of each point. We can eliminate half of them. These are those that are on the opposite side of the surface, as they will give zero contribution to the lighting. We still have a hemisphere. Now we can let random evenly distributed rays over this hemisphere, and stack the lighting in a heap, and then divide by the number of fired rays and multiply by 2π. At 2π, this is the area of a hemisphere with a radius of 1. Mathematicians will say that we have integrated lighting over the hemisphere by the Monte Carlo method.
How will this work in practice? We will pile up the texture using an additive blending using a floating point render. In the alpha channel of this texture we will record the number of our rays, and in rgb the actual lighting. This will allow us to split color.rgb into color.a and get the final image.
However, additive blending means that objects overlapped by other objects will begin to shine through others, as they will be drawn. To avoid this problem, we will use the depth prepass technique. The essence of the technique is that we first draw objects only into the depth buffer , and then switch the depth test to equal and draw the objects now into the color buffer .
So, then I generate a bunch of rays evenly distributed over the sphere:
function RandomRay(): TVec3; var theta, cosphi, sinphi: Single; begin theta := 2 * Pi * Random; cosphi := 1 - 2 * Random; sinphi := sqrt(1 - min(1.0, sqr(cosphi))); Result.x := sinphi * cos(theta); Result.y := sinphi * sin(theta); Result.z := cosphi; end; SetLength(Result, ACount); for i := 0 to ACount - 1 do Result[i] := Vec(RandomRay(), 1.0); and send this stuff as a constant to this shader:
float3 m_albedo; float3 m_f0; float m_roughness; static const float LightInt = 1.0; #define SamplesCount 1024 #define MaxSamplesCount 1024 float4 uLightDirections[MaxSamplesCount]; TextureCube uEnviroment; SamplerState uEnviromentSampler; PS_Output PS(VS_Output In) { PS_Output Out; Material_pbr m; m.albedo = m_albedo; m.f0 = m_f0; m.roughness = m_roughness; float3 MacroNormal = normalize(In.vNorm); float3 ViewDir = normalize(-In.vCoord); Out.Color.rgb = 0.0; [fastopt] for (uint i=0; i<SamplesCount; i++){ // float3 LightDir = dot(uLightDirections[i].xyz, In.vNorm) < 0 ? -uLightDirections[i].xyz : uLightDirections[i].xyz; // 180, float3 LightColor = uEnviroment.SampleLevel(uEnviromentSampler, mul(LightDir, (float3x3)V_InverseMatrix), 0.0).rgb*LightInt; // ( ) Out.Color.rgb += CookTorrance_GGX(MacroNormal, LightDir, ViewDir, m)*LightColor; // } Out.Color.rgb *= 2*PI; // Out.Color.a = SamplesCount; // return Out; } We start, and we see how our picture for the same balls gradually converges. I used two cubic cards for rendering. Here for this:
I took the cubic card that came with RenderMonkey. It is called Snow.dds. This is an LDR texture, and it is dull. Bulbs seem more dirty than beautifully lit.
And for this:

I took the HDR Probe from here: www.pauldebevec.com/Probes called Grace Cathedral, San Francisco. She has a dynamic range of 200,000: 1. See, what's the difference? Therefore, when you will do this kind of lighting, take the HDR texture immediately.
By the way, let's see what the law of conservation of energy holds. For this, I forcedly set the albedo in the shader to 1.0:
m.albedo = 1.0;
Light set in 1.0:
LightColor = 1.0;
Ideally, each pixel of the ball should now be equal to one. Therefore, everything that goes beyond the unit will be marked in red. I got this:

In fact, the red that is now - this error. It begins to converge, but at some point float accuracy is not enough, and convergence disappears. Please note that the right lower ball "turned blue". This is due to the fact that the Lambert model does not take into account the surface roughness, and the Cook-Torrens model does not take them into account with a polonster. In fact, we lost the yellow color that goes to F0 . Let's try to set F0 to all balls set to 1.0 and see:

The right balls became significantly darker due to the large roughness. In fact, this is a retroreflection that we lost. Cook-Torrens just loses this energy. The Oren-Nayar model can partially restore this energy. But we will postpone it for now. We'll have to accept the fact that for very rough models we lose up to 70% of retroreflection energy.
The source code is here . I already mentioned the collected binaries earlier, they are here .
3.2 Importance sampling
Of course, the gamer will not wait for the light in your picture to converge. Something needs to be done to avoid counting thousands and thousands of rays for each pixel. And the trick here is this. For Montecarlo, we considered a uniform distribution over the hemisphere. This is how we sampled:

but the real contribution comes from the part circled in pink. If we could choose the rays, mainly from the red zone, we would have received an acceptable picture much earlier. So we want this:

Fortunately for this there is a mathematical method called Importance Sampling (or sampling by significance). Significance in our expression introduces the parameter D. According to it, we can build a CDF (distribution function) from some PDF function (probability density function). For PDF, we take the micronormal distribution to our normal, the sum over the hemisphere will give one, which means we can write this integral:
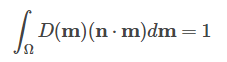
Here is the integrand - PDF
Taking the integral over the spherical angles, we get the following CDF :
For those who want to step by step go through this stage - you can look here .
For those who do not want / can not go deep say. We have a CDF , into which we substitute a uniformly distributed ξ , we get a distribution at the output that reflects our PDF . What does this mean for us?
1. That this will change our Cook-Torrens function. It will need to be divided into a PDF function.
2. The PDF function reflects the micronormal distribution relative to the macronormal. Previously, for Monte Carlo, we took a random vector, and took it as a vector to the light source. Now, using CDF, we choose a random vector H. Next, we reflect the vector of sight relative to this random H and obtain the vector of light.
3. Our PDF should be transferred to the view space (since it reflects the distribution along the vector N ). To translate, we need to divide our PDF into 4 * dot (H, V). It’s interesting for anyone to go deeper - go here and there are explanations in paragraph 4.1 and further with pictures in circles.
It seems that nothing is clear, right? Let's try to digest all this in code.
To begin with, we will write a function that generates the vector H from our CDF . In HLSL it will be like this:
float3 GGX_Sample(float2 E, float alpha) { float Phi = 2.0*PI*Ex; float cosThetha = saturate(sqrt( (1.0 - Ey) / (1.0 + alpha*alpha * Ey - Ey) )); float sinThetha = sqrt( 1.0 - cosThetha*cosThetha); return float3(sinThetha*cos(Phi), sinThetha*sin(Phi), cosThetha); } Here in E we give a uniform distribution [0; 1) for both spherical angles, in alpha we have a square from the roughness of the material.
At the output we get the H vector on the hemisphere. But this hemisphere needs to be oriented on the surface. To do this, we write another function that will return us the orientation matrix on the surface:
float3x3 GetSampleTransform(float3 Normal) { float3x3 w; float3 up = abs(Normal.y) < 0.999 ? float3(0,1,0) : float3(1,0,0); w[0] = normalize ( cross( up, Normal ) ); w[1] = cross( Normal, w[0] ); w[2] = Normal; return w; } On this matrix we will multiply all our generated vectors H , translating their tangent space into the space of the form. The principle is very similar to the TBN basis.
It now remains to divide our Cook-Torrens: G * D * F * 0.25 / (NV) into PDF . Our PDF = D * NH / (4 * HV) . Therefore, our modified Cook-Torrens is obtained:
G * F * HV / (NV * NH)
In HLSL, it now looks like this:
float3 CookTorrance_GGX_sample(float3 n, float3 l, float3 v, Material_pbr m, out float3 FK) { pdf = 0.0; FK = 0.0; n = normalize(n); v = normalize(v); l = normalize(l); float3 h = normalize(v+l); //precompute dots float NL = dot(n, l); if (NL <= 0.0) return 0.0; float NV = dot(n, v); if (NV <= 0.0) return 0.0; float NH = dot(n, h); float HV = dot(h, v); //precompute roughness square float roug_sqr = m.roughness*m.roughness; //calc coefficients float G = GGX_PartialGeometry(NV, roug_sqr) * GGX_PartialGeometry(NL, roug_sqr); float3 F = FresnelSchlick(m.f0, HV); FK = F; float3 specK = G*F*HV/(NV*NH); return max(0.0, specK); } Please note that I have thrown out the diffuse part from the Lambert illumination from this function, and return the FK parameter to the outside. The fact is that we cannot count the diffuse component through Importance Sampling , since our PDF is for facets that reflect light into our eyes. And the Lambert distribution does not depend on it. What to do? Hmm ... but let's leave the diffuse part black for the time being, and focus on speculation.
PS_Output PS(VS_Output In) { PS_Output Out; Material_pbr m; m.albedo = m_albedo; m.f0 = m_f0; m.roughness = m_roughness; float3 MacroNormal = normalize(In.vNorm); float3 ViewDir = normalize(-In.vCoord); float3x3 HTransform = GetSampleTransform(MacroNormal); Out.Color.rgb = 0.0; float3 specColor = 0.0; float3 FK_summ = 0.0; for (uint i=0; i<(uint)uSamplesCount; i++){ float3 H = GGX_Sample(uHammersleyPts[i].xy, m.roughness*m.roughness); // H H = mul(H, HTransform); // float3 LightDir = reflect(-ViewDir, H); // float3 specK; float3 FK; specK = CookTorrance_GGX_sample(MacroNormal, LightDir, ViewDir, m, FK); // FK_summ += FK; float3 LightColor = uRadiance.SampleLevel(uRadianceSampler, mul(LightDir.xyz, (float3x3)V_InverseMatrix), 0).rgb*LightInt;// specColor += specK * LightColor; // } specColor /= uSamplesCount; FK_summ /= uSamplesCount; Out.Color.rgb = specColor; Out.Color.a = 1.0; return Out; } We assign 1024 samples (without accumulation as in Monte Carlo) and look at the result:
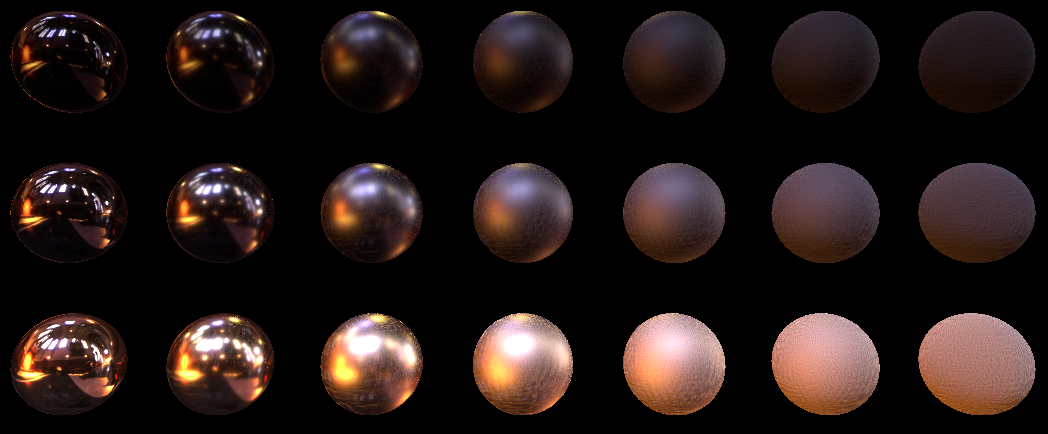
Although there are a lot of samples, but it turned out noisy. Especially on the big roughness.
3.3 Selecting LODs
This is because we take samples from a highly detailed map, from zero LOD . And it would be good for the rays having a large deviation to take a smaller LOD. The situation is well illustrated by this picture:

From this article from NVidia. The blue areas show the average value, which would be nice to take from the LOD textures. It can be seen that for more significant we take LOD less, and for less significant we take more, i.e. we take the value averaged over the region. It would be ideal if we covered the whole hemisphere with Lods. Fortunately, NVidia has already given us a ready-made (and simple formula):

This formula consists of the difference:
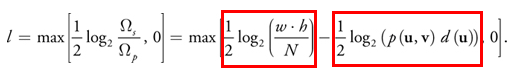
The left part of us depends on the size of the texture and the number of samples. This means that for all samples, we can count it once.On the right side we have a function p , which is nothing more than our pdf , and a function d , which they call distortion , but in fact there is a dependence on the angle of the sample to the observer. For d they have this formula:

Spoiler header
(, Dual-Paraboloid . , , b , . b=1.2 )
Well, NVidia is also recommended to make bias for Lods, add one. Let's see how it looks in the hlsl code. Here is our left side of the equation:
float ComputeLOD_AParam(){ float w, h; uRadiance.GetDimensions(w, h); return 0.5*log2(w*h/uSamplesCount); } Here we consider the right side, and immediately subtract it from the left:
float ComputeLOD(float AParam, float pdf, float3 l) { float du = 2.0*1.2*(abs(lz)+1.0); return max(0.0, AParam-0.5*log2(pdf*du*du)+1.0); } Now we see that we need to pass pdf and l values to ComputeLOD . l is the vector of the light sample, and pdf , if we look above then this is ours: pdf = D * dot (N, H) / (4 * dot (H, V)) . Therefore, let's add the returning pdf parameter to our CookTorrance_GGX_sample function :
float3 CookTorrance_GGX_sample(float3 n, float3 l, float3 v, Material_pbr m, out float3 FK, out float pdf) { pdf = 0.0; FK = 0.0; n = normalize(n); v = normalize(v); l = normalize(l); float3 h = normalize(v+l); //precompute dots float NL = dot(n, l); if (NL <= 0.0) return 0.0; float NV = dot(n, v); if (NV <= 0.0) return 0.0; float NH = dot(n, h); float HV = dot(h, v); //precompute roughness square float roug_sqr = m.roughness*m.roughness; //calc coefficients float G = GGX_PartialGeometry(NV, roug_sqr) * GGX_PartialGeometry(NL, roug_sqr); float3 F = FresnelSchlick(m.f0, HV); FK = F; float D = GGX_Distribution(NH, roug_sqr); // D pdf = D*NH/(4.0*HV); // pdf float3 specK = G*F*HV/(NV*NH); return max(0.0, specK); } And the cycle itself by samples now calculates LOD :
float LOD_Aparam = ComputeLOD_AParam(); for (uint i=0; i<(uint)uSamplesCount; i++){ float3 H = GGX_Sample(uHammersleyPts[i].xy, m.roughness*m.roughness); H = mul(H, HTransform); float3 LightDir = reflect(-ViewDir, H); float3 specK; float pdf; float3 FK; specK = CookTorrance_GGX_sample(MacroNormal, LightDir, ViewDir, m, FK, pdf); FK_summ += FK; float LOD = ComputeLOD(LOD_Aparam, pdf, LightDir); float3 LightColor = uRadiance.SampleLevel(uRadianceSampler, mul(LightDir.xyz, (float3x3)V_InverseMatrix), LOD).rgb*LightInt; specColor += specK * LightColor; } Let's look at what we did for 1024 samples with LODs:
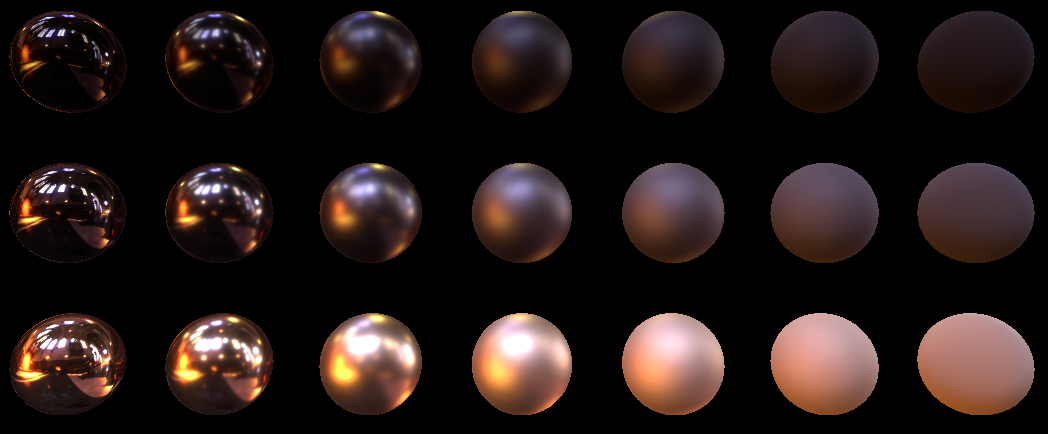
Looks perfect. Lower to 16, and ...
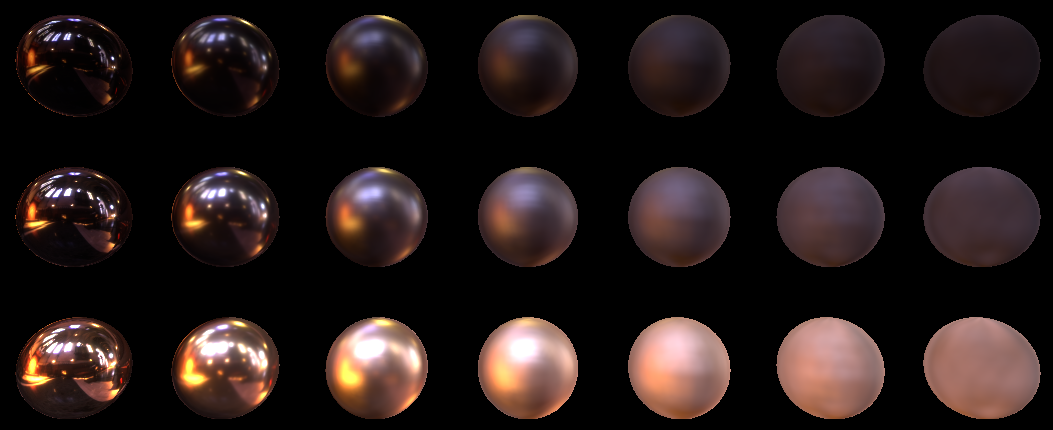
Yes, of course not quite perfect. It can be seen that the quality suffered on the balls with great roughness, but nevertheless, I consider this quality in principle acceptable. Additionally, it would be possible to improve the quality if we would build texture mip files based on our distribution. You can read about this in the Epic presentation here (see the Pre-Filtered Environment Map paragraph). In the meantime, in this article, I propose to focus on the classic pyramidal mipah.
3.4 Hammersley point set
If you look at our random rays, the drawback is clear. They are random. And we have already learned to read from lods and want to capture as much of our area as possible with our rays. To do this, we need to “spray” our rays, but taking into account the importance of sampling. Since Since CDF takes a uniform distribution, it is enough for us to evenly space points on the interval [0; 1) ... but our distribution should be two-dimensional. Therefore, it is necessary not only to evenly position the points on the gap, but also to make sure that the distance in Cartesian coordinates between the points is as large as possible. Hammersley point set is well suited for this role . A little more about this set of points can be read here .
I will only show a picture of the distribution:

I will also give a function that generates a single point:
function HammersleyPoint(const I, N: Integer): TVec2; function radicalInverse_VdC(bits: Cardinal): Single; begin bits := (bits shl 16) or (bits shr 16); bits := ((bits and $55555555) shl 1) or ((bits and $AAAAAAAA) shr 1); bits := ((bits and $33333333) shl 2) or ((bits and $CCCCCCCC) shr 2); bits := ((bits and $0F0F0F0F) shl 4) or ((bits and $F0F0F0F0) shr 4); bits := ((bits and $00FF00FF) shl 8) or ((bits and $FF00FF00) shr 8); Result := bits * 2.3283064365386963e-10; end; begin Result.x := I/N; Result.y := radicalInverse_VdC(I); end; What will our balls look like with this set of points? In fact, I faked, and all the above pictures for Importance Sampling were generated with a set of these points. On random sets of pictures look a little worse (believe a word?)
3.5 Irradiance map
Remember how we were left without a diffuse color? We cannot sample a diffuse color using importance sampling , because our importance sampling selects the most valuable rays for a speculator. For diffusion, the most valuable are directly opposite, on the macronormal surface. Fortunately, the diffuse component for Lambert is completely independent of the observer. Therefore, we can pre-calculate the lighting in a cubic map. And one more bonus - changing the angle so slightly affects the lighting that the pre-calculated map can be of very low resolution, for example 16 * 16 pixels per side.
This time we are lucky. We will not write code that builds the Irradiance map , but use the programCubeMapGen . Just open our cubemap (Load Cubemap (.dds)), set the Irradiance cubemap checkbox, select Output Cube Size 16:
and save the resulting cube map (for HDR textures, do not forget to set the desired output format for the texture).
Well, since we dealt with the Irradiance map , then after sampling we just add one sample from this map. Our HLSL code now looks like this:
Out.Color.rgb = 0.0; float3 specColor = 0.0; float3 FK_summ = 0.0; for (uint i=0; i<(uint)uSamplesCount; i++){ float3 H = GGX_Sample(uHammersleyPts[i].xy, m.roughness*m.roughness); H = mul(H, HTransform); float3 LightDir = reflect(-ViewDir, H); float3 specK; float pdf; float3 FK; specK = CookTorrance_GGX_sample(MacroNormal, LightDir, ViewDir, m, FK, pdf); FK_summ += FK; float LOD = ComputeLOD(LOD_Aparam, pdf, LightDir); float3 LightColor = uRadiance.SampleLevel(uRadianceSampler, mul(LightDir.xyz, (float3x3)V_InverseMatrix), LOD).rgb*LightInt; specColor += specK * LightColor; } specColor /= uSamplesCount; FK_summ /= uSamplesCount; float3 LightColor = uIrradiance.Sample(uIrradianceSampler, mul(MacroNormal, (float3x3)V_InverseMatrix)).rgb; Out.Color.rgb = m.albedo*saturate(1.0-FK_summ)*LightColor + specColor; And at the output we have the following picture for 16 samples:
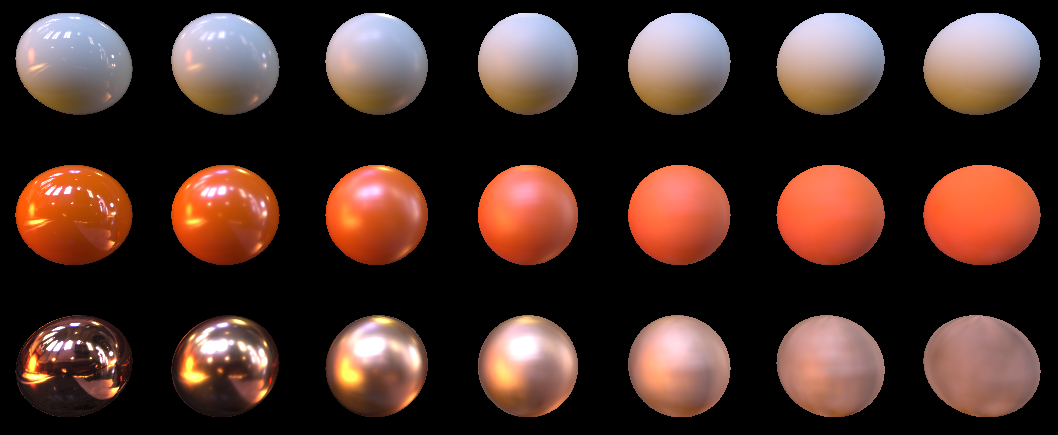
And such for 1024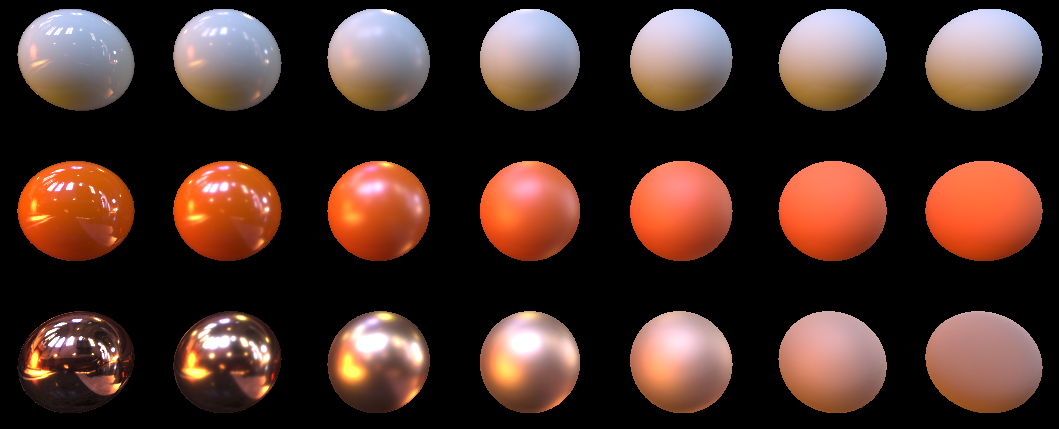
Please note that we no longer multiply the diffuse light by dot (N, L) , which is logical. After all, we predicted this illumination and baked it in a cubmap, and in our case N and L are generally the same vector.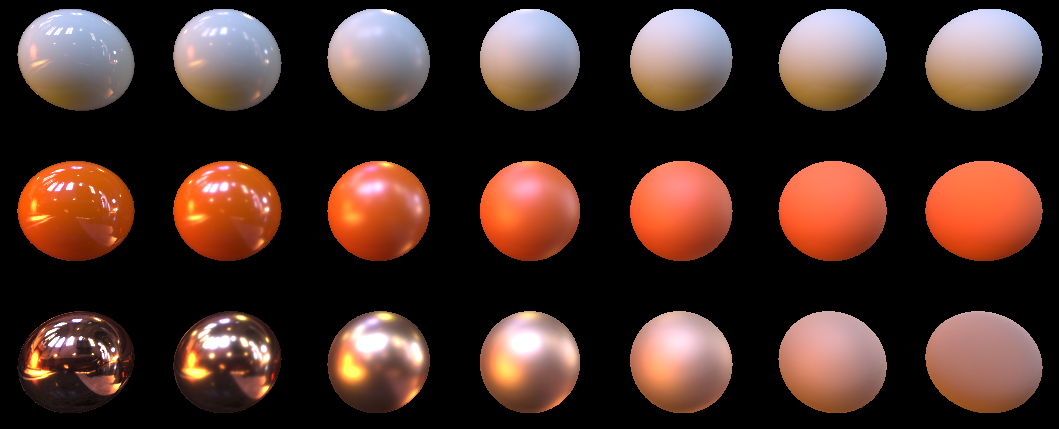
Let's look, what do we have there with energy conservation? As usual, we set the light from the cubic cards to one, set the material albedo to one, and highlight with a red area> 1. We get about this for 1024 samples:

And this is for 16:

As we see, there are obvious “outliers” of excess energy, but they are small. This is due to the fact that we do not accurately calculate the amount of light from the diffuse energy. After all, we consider Fresnel coefficients only for certain specula samples, and use them for all seeds that are pre-calculated in the irradiance map . Alas, I do not know what to do with it, the Internet could not tell me anything. Therefore, I propose for now to come to terms with this, all the same, the emissions of excess energy are not significant.
4 A little more about the materials.
While we were fiddling with the balls, you must have noticed that we have two float3 color options. This is albedo and f0 . Both of them have some physical meaning, but in games, as a rule, materials are divided into metals and non-metals. The fact is that non-metals always reflect the light in the grayscale ranges, but at the same time they re-radiate the curved light. Metals, on the contrary, reflect colored light, but at the same time absorb the rest.
That is, for metals we have:
albedo = {0, 0, 0}
f0 = {R, G, B}
for dielectrics we have:
albedo = {R, G, B}
f0 = {X, X, X}
and ... we see that we can enter a certain coefficient [0,1], which we will show as far as our metal surface, and take the material simply through linear interpolation. This is actually many artists do. I downloaded this 3d model.
Here, for example, the texture of the sword.
Texture of color:

Texture of roughness:

And finally, the texture of metallicity (the one about which I told above):

You can read a bit more about materials on the Internet. For example here .
Different engines and studios can pack the parameters in different ways, but as a rule, everything revolves around: color, roughness, metallicity.
And finally, how it looks on the whole model:

on the left is the same cathedral, which we tested on balls. On the right, our Artorias got into nature (the environment map from here www.pauldebevec.com/Probes is called Campus).
For rendering these image data, I used additional Reinhard tone mapping, but this topic is for a separate article.
The source code with the Artorias model is a demo in my framework, and is located here . I also compiled a version for you, and laid it out here .
5 Conclusion
The article came out much more than I expected. I wanted to tell more about:
1. Anisotropic lighting model
2. subsurface scattering
3. Advanced diffuse lighting model, such as Oren-Nayar
4. Grab spherical harmonics
5. Grab tonmapping
But believe it or not, I ran out of gas while writing this article ... And then everyone point is a fat layer. Therefore, there is, that is. Maybe someday I will tell about all this.
I hope that my article will lift the curtain of secrets hidden behind these letters PBR. And thank you for your attention.
Useful materials on PBR and so on
[1] blog.tobias-franke.eu/2014/03/30/notes_on_importance_sampling.html
PDF CDF, .
[2] hal.inria.fr/hal-00942452v1/document
PBR (+ )
[3] disney-animation.s3.amazonaws.com/library/s2012_pbs_disney_brdf_notes_v2.pdf
Disney, . ,
[4] blog.selfshadow.com/publications/s2015-shading-course/#course_content
Disney
[5] www.cs.cornell.edu/~srm/publications/EGSR07-btdf.pdf
GGX, Bruce Walter-
[6] de45xmedrsdbp.cloudfront.net/Resources/files/2013SiggraphPresentationsNotes-26915738.pdf
PBR Unreal Engine 4
[7] holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html
Hammersley Point Set
[8] www.jordanstevenstechart.com/physically-based-rendering
. .
[9] graphicrants.blogspot.nl/2013/08/specular-brdf-reference.html
[10] developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch20.html
NVidia Importance Sampling LOD-.
[11] cgg.mff.cuni.cz/~jaroslav/papers/2008-egsr-fis/2008-egsr-fis-final-embedded.pdf
Importance Sampling
[12] gdcvault.com/play/1024478/PBR-Diffuse-Lighting-for-GGX
PBR.
[13] www.codinglabs.net/article_physically_based_rendering.aspx
[14] www.codinglabs.net/article_physically_based_rendering_cook_torrance.aspx
( - )
[15] www.rorydriscoll.com/2009/01/25/energy-conservation-in-games
[16] www.gamedev.net/topic/625981-lambert-and-the-division-by-pi
www.wolframalpha.com/input/?i=integrate+cos+x+ *+sin+x+dx+dy+from+x+%3D+0+to+pi+%2F+2+y+%3D+0+to+pi+*+2
[17]https://seblagarde.files.wordpress.com/2015/07/course_notes_moving_frostbite_to_pbr_v32.pdf
[18] www.pauldebevec.com/Probes
HDR 360 . .
[19] seblagarde.wordpress.com/2012/06/10/amd-cubemapgen-for-physically-based-rendering
code.google.com/archive/p/cubemapgen/downloads
. radiance irradiance .
[20] eheitzresearch.wordpress.com/415-2
. .
PDF CDF, .
[2] hal.inria.fr/hal-00942452v1/document
PBR (+ )
[3] disney-animation.s3.amazonaws.com/library/s2012_pbs_disney_brdf_notes_v2.pdf
Disney, . ,
[4] blog.selfshadow.com/publications/s2015-shading-course/#course_content
Disney
[5] www.cs.cornell.edu/~srm/publications/EGSR07-btdf.pdf
GGX, Bruce Walter-
[6] de45xmedrsdbp.cloudfront.net/Resources/files/2013SiggraphPresentationsNotes-26915738.pdf
PBR Unreal Engine 4
[7] holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html
Hammersley Point Set
[8] www.jordanstevenstechart.com/physically-based-rendering
. .
[9] graphicrants.blogspot.nl/2013/08/specular-brdf-reference.html
[10] developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch20.html
NVidia Importance Sampling LOD-.
[11] cgg.mff.cuni.cz/~jaroslav/papers/2008-egsr-fis/2008-egsr-fis-final-embedded.pdf
Importance Sampling
[12] gdcvault.com/play/1024478/PBR-Diffuse-Lighting-for-GGX
PBR.
[13] www.codinglabs.net/article_physically_based_rendering.aspx
[14] www.codinglabs.net/article_physically_based_rendering_cook_torrance.aspx
( - )
[15] www.rorydriscoll.com/2009/01/25/energy-conservation-in-games
[16] www.gamedev.net/topic/625981-lambert-and-the-division-by-pi
www.wolframalpha.com/input/?i=integrate+cos+x+ *+sin+x+dx+dy+from+x+%3D+0+to+pi+%2F+2+y+%3D+0+to+pi+*+2
[17]https://seblagarde.files.wordpress.com/2015/07/course_notes_moving_frostbite_to_pbr_v32.pdf
[18] www.pauldebevec.com/Probes
HDR 360 . .
[19] seblagarde.wordpress.com/2012/06/10/amd-cubemapgen-for-physically-based-rendering
code.google.com/archive/p/cubemapgen/downloads
. radiance irradiance .
[20] eheitzresearch.wordpress.com/415-2
. .
Source: https://habr.com/ru/post/326852/
All Articles