One task about cactus graph

It is time for entrance exams, and therefore the solution of interesting problems. A couple of years ago, the Computer Science Center offered the applicants to deal with the task about the cactus graph, and today we will speak about it. Try to think about the task yourself, and then check with the decision.

By the way, the set in the CS center is already underway. This year, enrolling in full-time study is possible not only in St. Petersburg, but also in Novosibirsk. Come - in the classroom even more interesting.

Task

A cactus is a simple connected graph in which any two cycles have no more than one common vertex. Prove that the maximum number of edges in a cactus with n vertices is $$$\ operatorname {floor} \ frac {3} {2} (n-1)$.

* $$$\ operatorname {floor}$- rounding down.

Decision

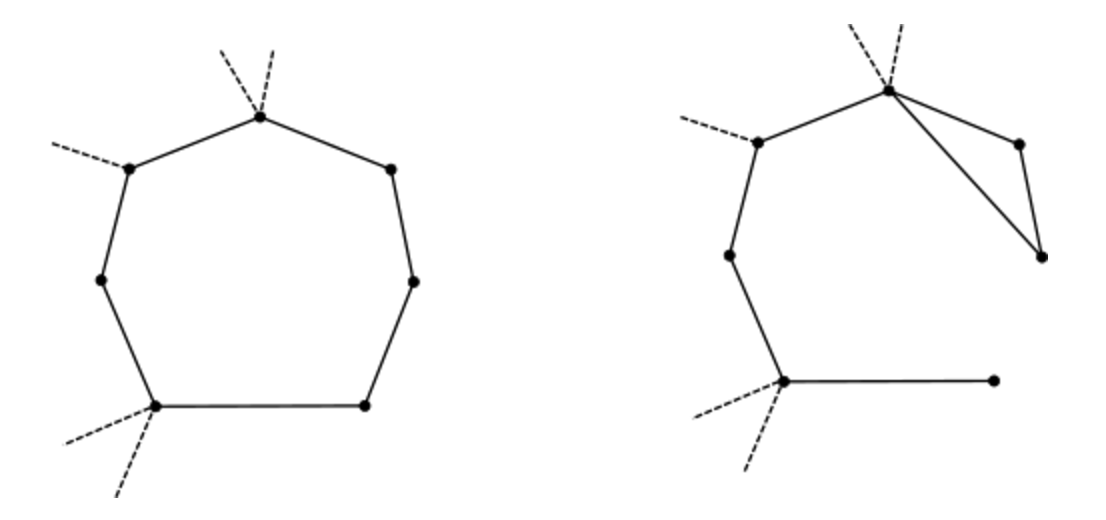
First you need to understand how this graph works. An example of the graph shown in the figure will help us in this. Next is a real cactus. This allows you to understand what caused this name.

Any cycle in which there are more than three vertices can be “tightened”, replacing it with a cycle of length three and a simple path. In this case, the total number of vertices and edges in the graph will not change, and the graph itself will remain a cactus. Below is an example of the "tightening" of the graph.

Consider now a cactus in which there are edges that do not lie on any cycle. Any two of these edges can be pulled to the top. As a result, two edges and two vertices will disappear from the graph. Then add to the graph a cycle of length three, one of the vertices of which will be the already existing vertex of the graph. The number of vertices will be the same, and the number of edges will increase by one.

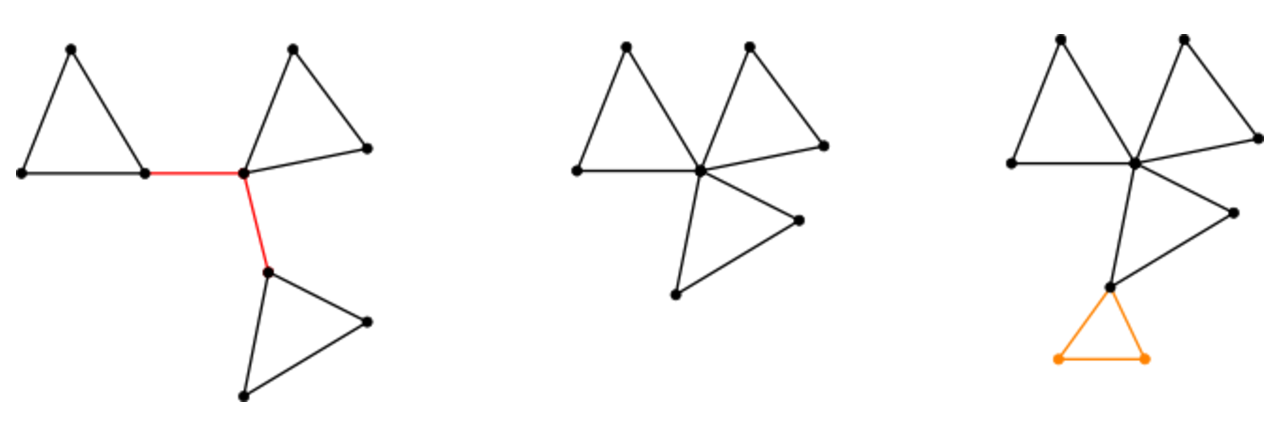
The figure above shows an example of the above manipulation. The left figure shows a cactus, in which the edges outside the cycles are highlighted. In the central drawing the same cactus, but already with tightened ribs. In it, not only two edges disappeared, but also became two peaks smaller. And finally, the right figure shows a cactus, to which we have added another triangle - three new edges and two vertices have appeared. As a result, the number of vertices before and after the operation did not change, and the number of edges increased.

Thus, the maximum number of edges in a cactus is achieved when it consists entirely of triangles and, perhaps, one edge that does not lie on any cycle. Such a cactus can be constructed by successively adding extreme triangle blocks, starting either with $$$K_3$either with $$$K_2$depending on parity $$$n$. ( $$$K_n$- full graph on $$$n$vertices.) When adding each block, two vertices and three edges are added, from which the assertion required in the problem immediately follows.