An important condition for the correctness of the constructed sketch is the consistency of the imposed restrictions. If less restrictions are imposed than required, some parameters cannot be unambiguously determined, therefore they can vary in a certain range of values. In such cases, it is said that the drawing has degrees of freedom (Degrees Of Freedom; DOF) . The analysis of degrees of freedom allows the design engineer to impose only necessary and sufficient number of restrictions, not allowing the system of equations to be overdetermined (overconstrained) , and not allowing to leave any degree of freedom without the imposed restrictions.
Part 1: Introduction
Part 2: Sketch
Part 3: Degrees of freedom and constraint equations
Part 4: "The ways of the Solver are inscrutable" or "Newton's Wormholes"

Redefining the system of equations is dangerous because a solution to such a system can be found, and this will not cause visible problems until the engineer changes the value of one of the conflicting constraints. In this case, there is a contradiction between the restrictions, and the system of equations becomes inconsistent , which means that it has no solutions. Without analyzing the degrees of freedom, it will be difficult to find conflicting constraints, since the drawings may contain hundreds of constraints.

When the number of constraints imposed is less than what is required to determine the values ​​of all unknown parameters, the system is called underconstraint . When designing parts such a case is dangerous and can lead to problems. For example, a design engineer can change the value of one constraint, and then return that value back. In the case of a fully defined drawing, these actions will work as a change-cancel, but in the case of an incomplete constraint, the values ​​of the free parameters may change.

Equations

To determine the relationship between the parameters of the drawing, you must specify them in the form of equations. Let's see what the basic equations look like, through which most of the constraints are given.

POINTS_COINCIDENT

Limit the coincidence of two points: just equalize their coordinates. Such an equation can be solved by the substitution method, eliminating two parameters from one of the points from consideration, replacing their references with the parameters of the coinciding point, and after solving the whole system, do the reverse substitution. This restriction removes 2 degrees of freedom.

HORIZONTAL / VERTICAL

Restrictions horizontal / vertical: here it is enough to equalize one of the coordinates of points. Restriction removes one degree of freedom.

PT_PT_DISTANCE

Limit the distance between points: it uses the Pythagorean theorem. Restriction removes one degree of freedom.

!

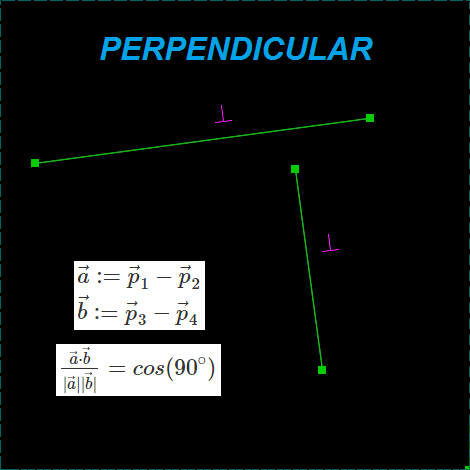
PERPENDICULAR

The perpendicularity of lines: the scalar product property is used to be proportional to the cosine of the angle between the vectors. Restriction removes one degree of freedom.

ANGLE

Limiting the angle between straight lines: all the same equation is used. Restriction removes one degree of freedom.

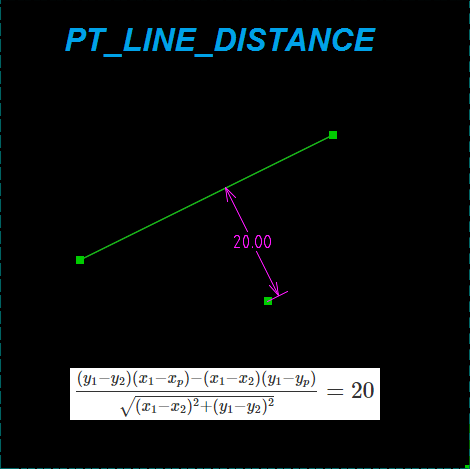
PT_LINE_DISTANCE

The limitation of the distance from the point to the line is written through the pseudoscalar (oblique) product and its property is used:

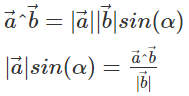
Where 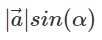and is the desired height.

Restriction removes one degree of freedom.

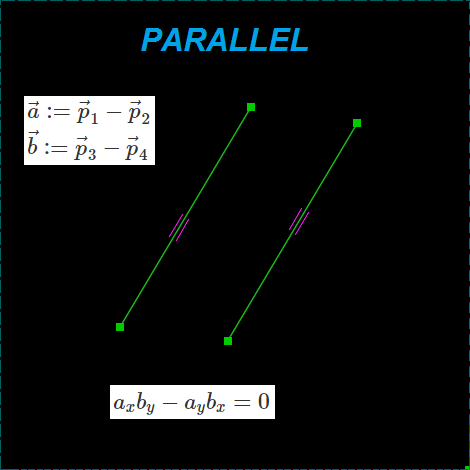
PARALLEL

The restriction of parallelism is also based on a pseudoscalar (skew) product. Here, the fact that sin (0) = 0 is used. To be honest, it would be necessary to divide the left side of the equation by the product of the modules of vectors, but historically the equation in SolveSpace is written this way. Since the zero result of the skew product leads to the equality to zero of the lengths of the vectors, the segments all the time tend to decrease. This does not interfere much if the length of the vectors is limited.

Conclusion

All other two-dimensional constraints are based on the above equations. In the next part we will get acquainted with the method of numerical solution of systems of equations, namely with Newton's method.

Part 1: Introduction
Part 2: Sketch
Part 3: Degrees of freedom and constraint equations
Part 4: "The ways of the Solver are inscrutable" or "Newton's Wormholes"