Recursive Moving Average Filter

Yes, dear reader, this also happens, and can be tasty and healthy!

As you probably already know, dear reader, there are two ways to build digital filters. These are recursive filters, they are also filters with infinite impulse response (IIR), and transversal filters, they are also filters with finite impulse response (FIR). The simplest and most widely used FIR filter is the “moving average filter”. The result of filtering such a filter is the arithmetic average of the last N samples of the input signal.
')


Or, in expanded form, for N = 4:



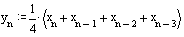
The function in C implements the moving average filter:

#define N (4) int filter(int a) { static int m[N]; static int n; m[n]=a; n=(n+1)%N; a=0; for(int j=0;j<N;j++){a=a+m[j];} return a/N; } 

The complex transfer coefficient of the moving average filter, normalized with respect to the sampling frequency, is defined as the Fourier transform of the impulse response:



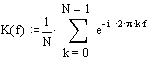
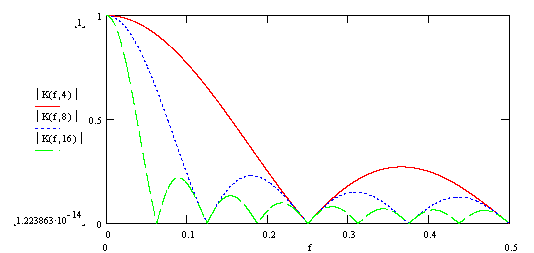
The graph of the amplitude-frequency characteristic (AFC), normalized to the sampling frequency, for different values ​​of the filter length (N = 4; 8; 16), is shown in the figure:



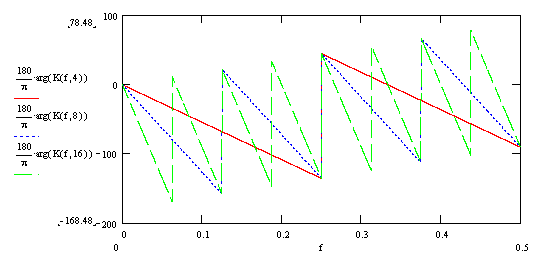
Accordingly, the graph of the phase-frequency characteristics (phase response):



This filter has found wide application in signal processing, in part because of its simplicity, but its most important feature is the linear phase-frequency characteristic, and, accordingly, the signal lag time constant throughout the frequency band. This filter transforms the amplitude spectrum of the signal, without affecting the phase, which makes it convenient to use in control systems. The moving average filter, due to its linear transient response, is widely used for linear interpolation, signal resampling, etc.

The main drawback of the moving average filter is the computational complexity proportional to the length of the filter N. To solve this problem, there is a recursive moving average filter. That is, a filter that has the same characteristics as a classic moving average filter, but implemented by a recursive scheme. These types of filters are widely known in narrow circles, and are called: recursive filters with linear phase response [Introduction to digital filtering. Under. ed. Bogner R. M: 1976] or CIC filters [ DspLib ]. There is a scientific school of prof. Turulina I.I. [ RSL ], engaged in the study of such filters.

Let us show a method for constructing a recursive moving average filter using the example of a filter with a length of N = 4. Subsequently, it will not be difficult to generalize the results to an arbitrary length of the filter.

As noted above, the value of the nth sample of the signal at the output of the filter can be defined as:



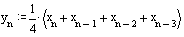
And the value of the previous ((n-1) -th) reference:



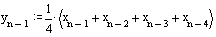
We subtract the second expression from the first expression, as a result we get:



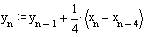
It is easy to figure out that with an arbitrary length of the filter N, the equation will be written in the following form:

(one)

Based on the above equation, you can write the filter code in the C language, but first we will check our calculations. Let us find the frequency characteristics of the recursive moving average filter, for which we perform the Z-transform of the filter equation. I want to remind the dear reader that in order to perform the Z-transformation, it is necessary to replace the variables (x _n , y _n ) with their Z-maps (X, Y), each decrease in the index of a variable by one corresponds to the multiplication Z ^-1 .



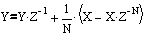
Solve the resulting equation for the Y / X filter ratio



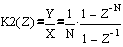
We move from the Z-domain to the frequency domain, replacing 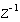on 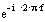and we get the complex transfer ratio: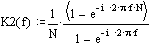



We construct a graph of the module of the complex transmission coefficient (frequency response of the filter), for various values ​​of N = 4,8,16:



As well as the argument of the complex transfer coefficient (filter phase response):



As can be seen from the graphs, the frequency characteristics of the classic moving average filter and the recursive moving average filter are completely the same.

Let us turn to the implementation of the filter. With the direct implementation of the filter equation (1) in terms of integer arithmetic, some difficulties are possible. When performing the division by N in integer arithmetic there is a loss of significant digits, which leads to nonlinear distortion of the signal at the output of the filter. To solve these difficulties, it is necessary to eliminate the division operation from the recurrent filter equation. Why multiply both sides of the filter equation (1) by N.



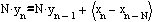
In the resulting expression, perform the substitution:




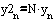
As a result, the filter equation (1) is converted into a system of equations:




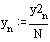
Based on the system of filter equations, we write the code that implements the filter in C.

 #define N (4) int filter(int x) { static int n; static int m[N]; static int y; y=y+(xm[n]); m[n]=x; n=(n+1)%N; return y/N; } 

It should be noted that fans of the “perfect code” can impose restrictive requirements on the filter length N. With a filter length equal to powers of two (2,4,8,16 ...), you can replace the division operation (/) with an arithmetic shift (>>), the remainder of the division operation (%) is a bit-wise conjunction (&).

Conclusion

Dear reader, the purpose of this publication is not so much to acquaint you with the recursive moving average filter, it may very well be that you know very well about it. The purpose of this publication is to acquaint you, dear reader, with some practical methods of analysis and synthesis of digital filters. See how simple we are from a transversal filter to a recursive filter, and the Z-transform is not as scary as it is painted. I also hope that the method of increasing the accuracy of calculating recurrent expressions in terms of integer arithmetic will be useful to you.

Successes to you, dear reader!