Spectral analysis of signals from non-linear links of ACS in Python

Objective

In my article [1], the harmonic linearization method is considered for the study of control systems containing nonlinear elements.

This method can be used in the case when the linear part of the system is a low-pass filter, i.e. filters out all harmonic components arising at the output of a nonlinear element, except for the first harmonic [2]. Therefore, a logical continuation of my first article will be a harmonic analysis of the considered nonlinear elements. In addition, you need to consider a hardware alternative to the harmonic linearization method.

Analysis Method and Program Code

Let a non-linear element receive a pure sine wave signal. By the method of decomposition into a discrete Fourier series, we obtain its spectrum.
')

#!/usr/bin/env python #coding=utf8 from numpy import array, arange, abs as np_abs from numpy.fft import rfft, rfftfreq from math import sin, pi import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' FD = 250000# ,    N = 2500#  , N/FD  F=250.0#    w=(2.*pi*F/FD)#   A=3.0#  B=0.5#  #      F  N sin_sig = array([A*sin(w*t) for t in range(N)])#  plt.plot(arange(N)/float(FD), sin_sig, 'r') plt.xlabel(', .') plt.ylabel(' ') plt.title('  ') plt.grid(True) plt.show() spectr_sin = rfft(sin_sig )#   rfft   plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sin)/N) #  plt.xlabel(', ') plt.ylabel(' ') plt.title('  ') plt.grid(True) plt.show() 

Get the signal and the spectrum of the signal from the output of the nonlinear element with "saturation".

 #    c «»  A*sin(w*t)  abs()>abs(B) sinp_sig =array([A*sin(w*t) if abs(A*sin(w*t))<B else A*sin(w*t)*B/abs(A*sin(w*t)) for t in range(N)]) plt.plot(arange(N)/float(FD), sinp_sig, 'r')#  plt.xlabel(', .') plt.ylabel(' ') plt.title('  c ') plt.grid(True) plt.show() spectr_sinp = rfft(sinp_sig ) plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sinp)/N)#  plt.xlabel(', ') plt.ylabel(' ') plt.title('   ') plt.grid(True) plt.show() 

To account for the sign of restriction B, the following code is used - A * sin (w * t) * B / abs (A * sin (w * t)).

We obtain the type of signal and the spectrum of the nonlinear element with the transition amplitude to zero.

 #    «c   »  A*sin(w*t)  abs()=abs(B) sinn_sig = array([A*sin(w*t) if abs(A*sin(w*t))<B else 0 for t in range(N)]) plt.plot(arange(N)/float(FD), sinn_sig, 'r') plt.xlabel(', .') plt.ylabel(' ') plt.title('  c ') plt.grid(True) plt.show() spectr_sinn = rfft(sinn_sig ) plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sinn)/N)#  plt.xlabel(', ') plt.ylabel('    ') plt.title('   ') plt.grid(True) plt.show() 

results

The signal at the input and output of nonlinear elements.







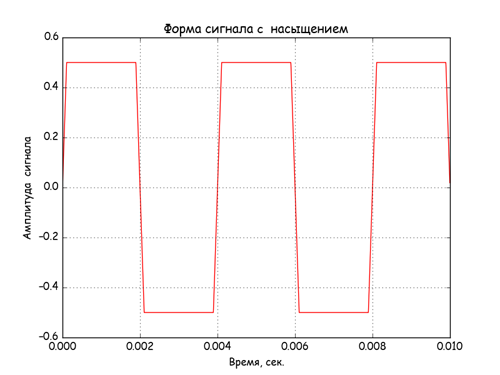
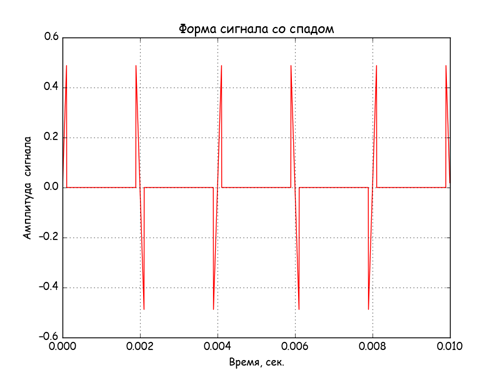
Spectra of signals at the output of nonlinear elements.





A non-linear element with a decay signal generates a large number of high-frequency harmonics. To filter the signal at the output of nonlinear elements, you can apply a digital low-pass filter, described in detail in [3]. To study the possibilities of digital filtering of signals of nonlinear elements in the program code [3], the following changes were made.

 A=1.0 B=0.4 test_n = 2560 # -    test_f = 200 #        test_period_count = 10.0 # -    test_t = numpy.linspace(0.0, test_period_count/test_f, test_n) #   sin(wt),    test_base_signal = array([A*sin(2*pi*test_f* i) for i in test_t ]) test_signal =array([A*sin(2*pi*test_f* i) if abs(sin(2*pi*test_f* i))<B else 0 for i in test_t ]) #test_signal=array([A*sin(2*pi*test_f* i) if abs(A*sin(2*pi*test_f* i))<B else A*sin(2*pi*test_f* i)*B/abs(A*sin(2*pi*test_f* i)) for i in test_t ])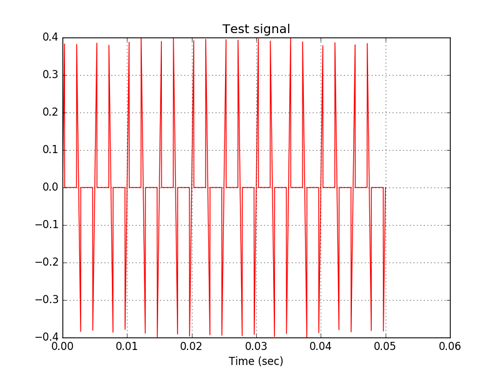 

The signal spectrum at the output of the filter.

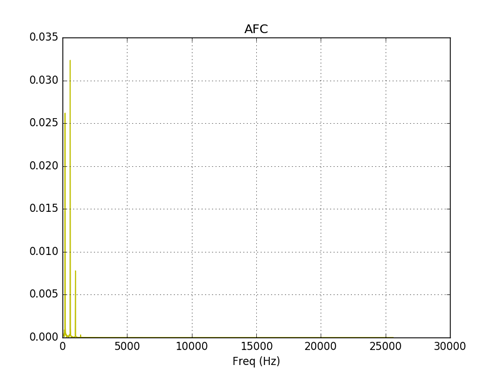
Conclusion

You can solve the problem of using nonlinear elements using a microprocessor in hardware, but you need to match the signal levels, as well as the DAC and ADC.

Links

1. The method of harmonic linearization means of Python
2. The method of harmonic linearization
3. Digital filter