FPGA image rotation

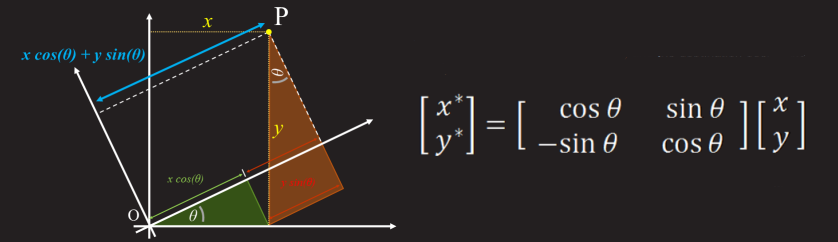
Half a year ago, I came across this video here .

The first thought was that it was very cool and I could never do that again. Time passed, articles were read, methods were studied, and I looked for examples of how to implement this, but to my chagrin, nothing concrete was found on the network. Once I stumbled upon the calculations of trigonometric functions using the CORDIC algorithms, I decided to try creating my own image rotator on the FPGA.

CORDIC

So, CORDIC is an abbreviation for CO ordinate R otation D Igital C omputer.
')
It is a powerful tool for calculating hyperbolic and trigonometric functions. Most CORDIC algorithms work in a sequential approximation method and are not very difficult to implement in both high-level programming languages ​​and HDL. I will not focus on the math method, the reader can read it on the network or on the links below.

In free access, I came across this implementation of the CORDIC algorithm in verilog. This core works in 2 modes: Rotate and Vector . Rotate mode is suitable for our purposes. It allows you to calculate the values ​​of the functions sin and cos from a given angle in radians or degrees. The library can be configured both in the pipeline and in the combination version. For our purposes, the pipeline is suitable, it has the largest Fmax . It will produce sine and cosine values ​​with a delay of 16 cycles.

In the RTL Viewer-e CORDIC module is displayed consisting of 16 blocks of the same type:


Each of which accepts input from the previous one and outputs connected to the inputs of the next. It looks like this:



The library core works only in the first quadrant, and this means that we will have to calculate the remaining three by subtracting pi / 2 and changing the sign.

The approach I have chosen is not very correct. The quality of the rotated image leaves much to be desired. This is due to the calculation of coordinates on the fly, without the use of additional data buffering and sequential calculation of coordinates for several passes, as is done in Shear .

The first instance of our rotator is the block for calculating the quadrant and the angle of rotation. The rotation angle is incremented by each new frame by 1 degree. Upon reaching an angle of 90 degrees, the quadrant changes to the next one in turn, and the angle is either reset to zero or decremented by 1 degree each new frame.

It looks like this:

always @(posedge clk) begin if (!nRst) begin cordic_angle <= 17'd0; cordic_quadrant <= 2'd0; rotator_state <= 2'd0; end else begin if (frame_changed) begin case (rotator_state) 2'd0: begin if (cordic_angle[15:8] == 8'd89) begin cordic_quadrant <= cordic_quadrant + 1'b1; rotator_state <= 2'd1; end else cordic_angle[15:8] <= cordic_angle[15:8] + 1'b1; end 2'd1: begin if (cordic_angle[15:8] == 8'd1) begin cordic_quadrant <= cordic_quadrant + 1'b1; rotator_state <= 2'd0; end else cordic_angle[15:8] <= cordic_angle[15:8] - 1'b1; end default: rotator_state <= 2'd0; endcase end end end 

Next, the angle value is fed to the CORDIC module, which calculates the values ​​of sin and cos.

 cordic CORDIC( .clk(clk), .rst(~nRst), .x_i(17'd19896), .y_i(16'd0), .theta_i(cordic_angle), .x_o(COS), .y_o(SIN), .theta_o(), .valid_in(), .valid_out() ); 

Further, it is not difficult to guess that the calculation of the coordinates of each subsequent pixel will be made using the formula:

x '= cos (angle) * x - sin (angle) * y;
y '= sin (angle) * x + cos (angle) * y;



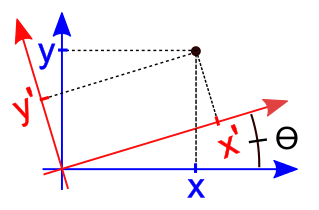
If you leave everything in this form, then the rotation will be centered at the origin. This rotation does not suit us, we need the image to rotate around its axis with the center in the middle of the image. To do this, we need to conduct calculations relative to the center of the image.

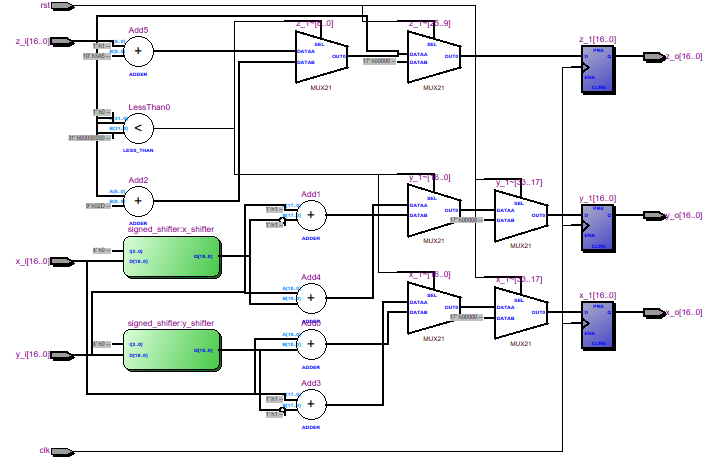
 parameter PRECISION = 15; parameter OUTPUT = 12; parameter INPUT = 12; parameter OUT_SIZE = PRECISION + OUTPUT; parameter BUS_MSB = OUT_SIZE + 2; wire [15:0] res_x = RES_X - 1'b1; wire [15:0] res_y = RES_Y - 1'b1; assign dx = {1'b0, RES_X[11:1]}; assign dy = {1'b0, RES_Y[11:1]}; always @(posedge clk) begin delta_x <= dx << PRECISION; delta_y <= dy << PRECISION; nd 

Next, we calculate the values ​​cos (angle) * x, sin (angle) * x, cos (angle) * y, sin (angle) * y.
You can calculate it like this:

 always @(posedge clk) begin mult_xcos <= (xi - dx) * COS; mult_xsin <= (xi - dx) * SIN; mult_ycos <= (yi - dy) * COS; mult_ysin <= (yi - dy) * SIN; end 

But I decided to use megafunctions lpm_mult . Their use significantly increases Fmax .

 reg signed [BUS_MSB: 0] tmp_x, tmp_y, mult_xsin, mult_xcos, mult_ysin, mult_ycos; reg signed [BUS_MSB: 0] delta_x = 0, delta_y = 0; wire signed [11:0] dx, dy; reg signed [BUS_MSB: 0] mxsin, mxcos, mysin, mycos; reg signed [11:0] ddx, ddy; always @(posedge clk) begin ddx <= xi - dx; ddy <= yi - dy; end wire signed [BUS_MSB-1: 0] mult_xcos1; wire signed [BUS_MSB-1: 0] mult_xsin1; wire signed [BUS_MSB-1: 0] mult_ycos1; wire signed [BUS_MSB-1: 0] mult_ysin1; lpm_mult M1(.clock(clk), .dataa(COS), .datab(ddx), .result(mult_xcos1)); defparam M1.lpm_widtha = 17; defparam M1.lpm_widthb = 12; defparam M1.lpm_pipeline = 1; defparam M1.lpm_representation = "SIGNED"; lpm_mult M2(.clock(clk), .dataa(SIN), .datab(ddx), .result(mult_xsin1)); defparam M2.lpm_widtha = 17; defparam M2.lpm_widthb = 12; defparam M2.lpm_pipeline = 1; defparam M2.lpm_representation = "SIGNED"; lpm_mult M3(.clock(clk), .dataa(COS), .datab(ddy), .result(mult_ycos1)); defparam M3.lpm_widtha = 17; defparam M3.lpm_widthb = 12; defparam M3.lpm_pipeline = 1; defparam M3.lpm_representation = "SIGNED"; lpm_mult M4(.clock(clk), .dataa(SIN), .datab(ddy), .result(mult_ysin1)); defparam M4.lpm_widtha = 17; defparam M4.lpm_widthb = 12; defparam M4.lpm_pipeline = 1; defparam M4.lpm_representation = "SIGNED"; 

After multiplication, we obtain products whose sign we need to change in each of the following quadrants:

 always @(posedge clk) begin mxcos <= mult_xcos1; mxsin <= mult_xsin1; mycos <= mult_ycos1; mysin <= mult_ysin1; case (cordic_quadrant) 2'd0: begin mxsin <= -mult_xsin1; end 2'd1: begin mxcos <= -mult_xcos1; mxsin <= -mult_xsin1; mycos <= -mult_ycos1; end 2'd2: begin mxcos <= -mult_xcos1; mysin <= -mult_ysin1; mycos <= -mult_ycos1; end 2'd3: begin mysin <= -mult_ysin1; end endcase end 

Now it remains for the small - to calculate the pixel coordinates themselves:

 /* I II III IV + + + - - - - - + - + + + - - + */ always @(posedge clk) begin tmp_x <= delta_x + mxcos + mysin; tmp_y <= delta_y + mycos + mxsin; end wire [15:0] xo = tmp_x[BUS_MSB] ? 12'd0: tmp_x[OUT_SIZE-1:PRECISION]; wire [15:0] yo = tmp_y[BUS_MSB] ? 12'd0: tmp_y[OUT_SIZE-1:PRECISION]; 

We cut the pixels that go beyond the image:

 wire [11:0] xo_t = (xo[11:0] > res_x[11:0]) ? 12'd0 : xo[11:0]; wire [11:0] yo_t = (yo[11:0] > res_y[11:0]) ? 12'd0 : yo[11:0]; 

And his address in memory:

 //addr_out <= yo[11:0] * RES_X + xo[11:0]; 

And again we use lpm_mult:

 reg [11:0] xo_r, yo_r; always @(posedge clk) begin xo_r <= xo_t; yo_r <= yo_t; end wire [28:0] result; lpm_mult M5(.clock(clk), .dataa(RES_X[11:0]), .datab(yo_r[11:0]), .result(result)); defparam M5.lpm_widtha = 12; defparam M5.lpm_widthb = 12; defparam M5.lpm_pipeline = 1; defparam M5.lpm_representation = "UNSIGNED"; always @(posedge clk) addr_out <= result[22:0] + xo_r[11:0]; 

That's all!

Method problems

As I mentioned above, this approach has many drawbacks. Because of the calculation error, holes appear in the output image; the larger the angle of rotation, the larger the holes. This also happens by the fact that the size of the new image is larger than that of the original. This effect will be aliasing and there are methods of dealing with it, for example, the median filter reviewed in my previous article .

Before each subsequent frame it would not hurt to clean the memory from the previous frame so that the new image is obtained on a clean background, but it takes time and you have to skip one frame.

The only advantage of the method is the ease of implementation and processing speed, since coordinates are calculated on-the-fly.

That's what came out of it

Related Links

→ CORDIC in Russian
→ CORDIC for dummies
→ CORDIC FAQ

Quartus Project Archive

→ Link to Yandex disk.