Probability of data loss in large clusters
This article uses MathJax for rendering mathematical formulas. Javascript must be enabled for MathJax to work.
Many distributed storage systems (including Cassandra, Riak, HDFS, MongoDB, Kafka, ...) use replication for data integrity. They are usually deployed in a “ just a bunch of disks” configuration (Just a bunch of disks, JBOD) —that is, without any RAID for failover. If one of the disks in the node fails, then the data of this disk is simply lost. To prevent irretrievable data loss, the DBMS stores a copy (replica) of data somewhere on disks in another node.
The most common replication factor is 3, which means that the database stores three copies of each piece of data on different disks connected to three different computers. The explanation for this is approximately the following: disks fail rarely. If the disk is out of order, then there is time to replace it, and at this time you have two more copies from which you can recover data to a new disk. The risk of failure of the second disk, while you restore the first one, is low enough, and the probability of death of all three disks at the same time is so small that it is more likely to die from an asteroid hit.
Let us estimate on a napkin: if the probability of failure of one disk in a certain period of time is 0.1% (to choose an arbitrary number), then the probability of failure of two disks is (0.001) 2 = 10 -6 , and the probability of failure of three disks is (0.001 ) 3 = 10 -9 , or one in a billion. These calculations suggest that disk failures occur independently of each other - which in reality is not always true, for example, disks from the same batch from one manufacturer may have similar defects. But for our approximate calculations will come down.
')
For now common sense prevails. It sounds reasonable, but unfortunately for many storage systems this does not work. In the article I will show why.
If your database cluster really consists of only three machines, then the probability of simultaneous failure of all three is really very small (except for correlated failures, such as a fire in the data center). However, if you switch to larger clusters, the probabilities change. The more nodes and disks in your cluster, the greater the likelihood of data loss.
This is a counterintuitive idea. “Of course,” you think, “each piece of data is still replicated on three disks. The probability of a disk failure does not depend on the cluster size. So why does cluster size matter? ”But I calculated the probabilities and drew a graph that looks like this:
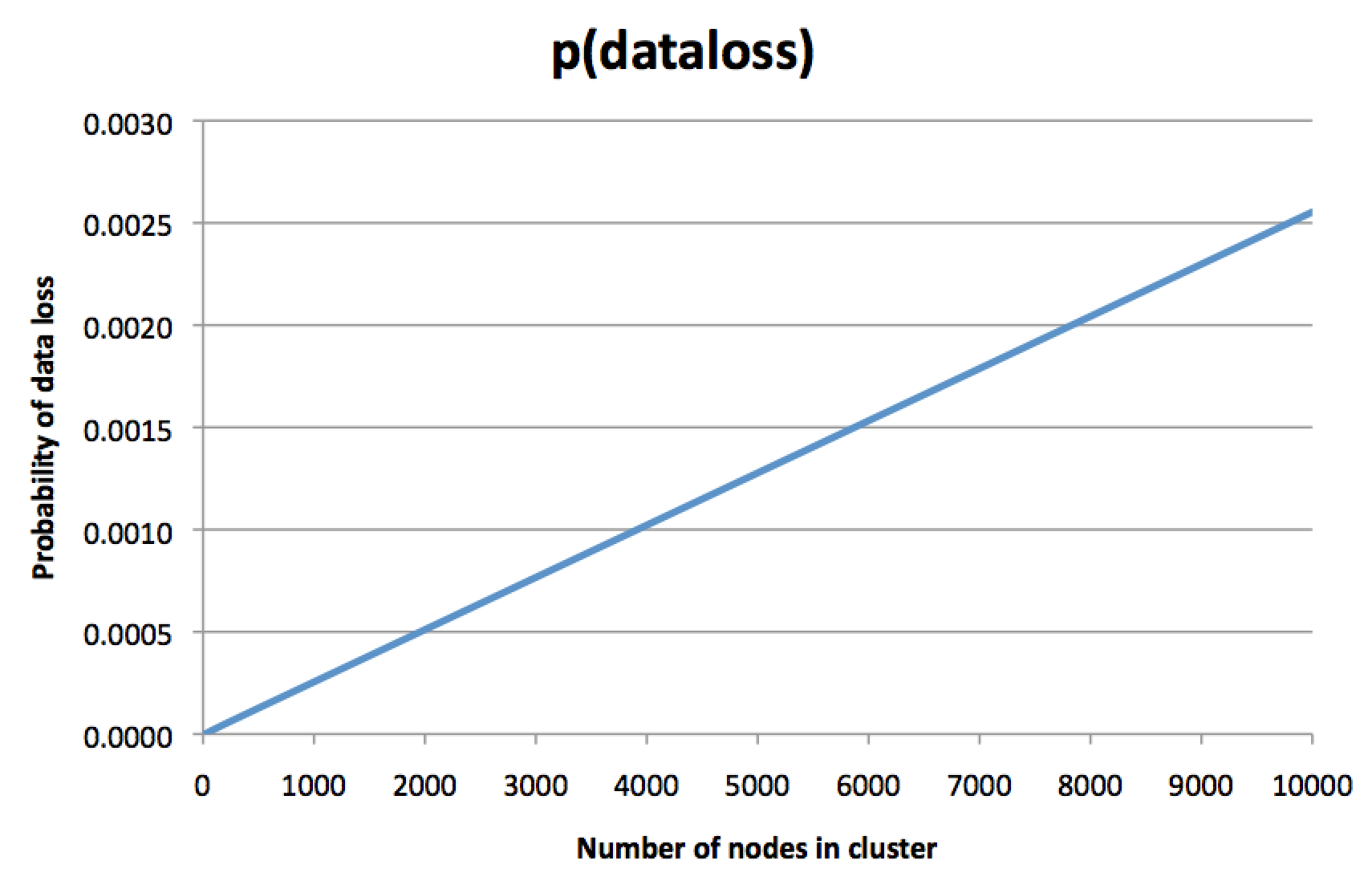
For clarity, not the probability of failure of one node is indicated here, but the probability of irreversible loss of three replicas of some piece of data, so restoring from a backup (if you have one) will remain the only way to recover data. The larger the cluster, the more likely the loss of data. Probably, you did not expect this when you decided to pay for the replication factor 3.
In this graph, the y-axis is slightly arbitrary and depends on many assumptions, but the very direction of the graph is frightening. If we assume that a node has a 0.1% failure rate for a certain period of time, the graph shows that in a cluster of 8000 nodes, the chance of irreversible loss of all three replicas for some piece of data (for the same period of time) is about 0.2%. Yes, you read it correctly: the risk of losing all three copies of the data is almost twice as high as the risk of losing one node! What then is the meaning of replication?
Intuitively, this graph can be interpreted as follows: in a cluster of 8000 nodes, almost certainly several nodes are always dead at each moment of time. This is normal and not a problem: a certain level of failures and replacement of nodes was assumed as part of routine maintenance. But if you are unlucky, then there is a piece of data for which all three replicas were included in the number of those nodes that are now dead - and if this happened, then your data is lost forever. Lost data makes up only a small part of the entire data set in a cluster, but this is still bad news, because when using replication factor 3 you usually think “I don’t want to lose data at all” rather than “I don’t care about occasional loss of a small amount of data there are few of them. ” Maybe this particular piece of lost data is really important information.
The probability that all three replicas belong to the number of dead nodes is crucially dependent on the algorithm that the system uses to distribute data among replicas. The graph at the top is calculated with the assumption that the data is divided into sections (shards), and each section is stored on three randomly selected nodes (or pseudo-randomly with a hash function). This is a case of sequential hashing , which is used in Cassandra and Riak, among others (as far as I know). I'm not sure how the replica assignment works in other systems, so I will be grateful for the hints of those who know the features of the various storage systems.
Let me show you how I calculated the top graph using a probabilistic model of a replicated database.
Suppose that the probability of losing an individual node is . We ignore the time in this model, and just look at the probability of failure in some arbitrary period of time. For example, it may assume that - This is the probability of a node failing on a certain day, which makes sense if it takes about one day to replace the node and restore the lost data to new disks. For simplicity, I will not distinguish between a node failure and a disk failure , but I will take into account only irreversible failures (ignoring failures when the node returns to operation after a reboot).
Let be will be the number of nodes in the cluster. Then the probability that of the node has failed (assuming that the failures are independent of each other) corresponds to the binomial distribution :
Member - this is the probability that node failed member - the probability that the remaining remained in service, and - is the number of different ways to choose of nod. interpreted as the number of combinations of by . This binomial coefficient is calculated as:
Let be will be a replication factor (usually ). Assuming that of node failed, what is the probability that a particular partition has all your replicas on failed nodes?
Well, in a system with sequential hashing, each partition is assigned to the nodes in an independent and random (or pseudo-random) manner. For this section there is different ways to assign replicas of nodes, and all of these assignments can happen with the same probability. Moreover, there is different ways to choose replicas of failed nodes are ways in which all replicas can be assigned to failed nodes. Now let's calculate the part of the assignments that leads to the failure of all replicas:
(The vertical bar after “partition lost” means “under condition” and indicates a conditional probability : the probability is given under the assumption that node failed).
So, here is the chance that all replicas of one particular partition are lost. What about cluster with sections? If one or more partitions are lost, we lose data. Therefore, in order not to lose data, it is necessary that all sections were not lost:
Cassandra and Riak refer to sections as vnodes, but this is the same. In general, the number of sections does not depend on the number of nodes . In the case of Cassandra, there is usually a fixed number of sections on the node ; default (set by the
Having collected everything in one place, we can now calculate the probability of losing one or more sections in a cluster of size with replication factor . If the number of failures less than the replication factor, then we can be sure that no data is lost. Therefore, you should add probabilities for all possible values by the number of failures. with :
This is a slightly excessive, but it seems to me an accurate assessment. And if you substitute , and and check the values from 3 to 10,000, then get a graph at the top. I wrote a small Ruby program for this calculation.
You can get a simpler approximation using the union boundary :
Even if the failure of one section is not independent of the failure of another section, this approximation is still applicable. And it seems that it quite closely corresponds to the exact result: on the graph, the probability of data loss looks like a straight line, proportional to the number of nodes.
The approximation says that this probability is proportional to the number of partitions, which is the same based on a fixed number of 256 partitions per node.
Moreover, if we substitute the number of 10,000 nodes in the approximation, we get which closely matches the output from the Ruby program.
Is this a problem in practice? I do not know. Basically, I think this is an interesting counterintuitive phenomenon. I heard rumors that this led to real data loss in companies with large clusters of databases, but I didn’t see the problem being documented somewhere. If you are aware of discussions on this topic, please show me.
Calculations show that to reduce the likelihood of data loss, reduce the number of partitions or increase the replication factor. Using more replicas costs money, so this is not the ideal solution for large clusters that are already expensive. However, changing the number of sections represents an interesting compromise. Cassandra initially used one partition per node, but a few years ago switched to 256 sections per node to achieve better load balancing and more efficient rebalancing. The reverse side, as can be seen from the calculations, was a much higher probability of losing at least one of the sections.
I think it is possible to develop an algorithm for assigning replicas, in which the probability of data loss does not grow with the cluster size or at least does not grow so fast, but where at the same time the properties of a good load distribution and balance recovery are preserved. This would be an interesting area for further research. In this context, my colleague Stefan noticed that the expected rate of data loss remains unchanged in a cluster of a certain size, regardless of the replica assignment algorithm — in other words, you can choose between a high probability of losing small amounts of data and a low probability of losing large amounts of data! Do you think the second option is better?
You need really large clusters before this effect really manifests itself, but clusters of thousands of nodes are used in different large companies, so it would be interesting to hear people with experience on this scale. If the probability of irreversible data loss in a cluster of 10,000 nodes is indeed 0.25% per day, this means a 60% chance of data loss per year. This is much more than the chance of “one in a billion” to die-from an asteroid, which I mentioned at the beginning.
Are architects of distributed data systems aware of the problem? If I understand correctly, here something should be considered when designing replication schemes. Perhaps this post will draw attention to the fact that just having three replicas does not make you feel safe.
Many distributed storage systems (including Cassandra, Riak, HDFS, MongoDB, Kafka, ...) use replication for data integrity. They are usually deployed in a “ just a bunch of disks” configuration (Just a bunch of disks, JBOD) —that is, without any RAID for failover. If one of the disks in the node fails, then the data of this disk is simply lost. To prevent irretrievable data loss, the DBMS stores a copy (replica) of data somewhere on disks in another node.
The most common replication factor is 3, which means that the database stores three copies of each piece of data on different disks connected to three different computers. The explanation for this is approximately the following: disks fail rarely. If the disk is out of order, then there is time to replace it, and at this time you have two more copies from which you can recover data to a new disk. The risk of failure of the second disk, while you restore the first one, is low enough, and the probability of death of all three disks at the same time is so small that it is more likely to die from an asteroid hit.
Let us estimate on a napkin: if the probability of failure of one disk in a certain period of time is 0.1% (to choose an arbitrary number), then the probability of failure of two disks is (0.001) 2 = 10 -6 , and the probability of failure of three disks is (0.001 ) 3 = 10 -9 , or one in a billion. These calculations suggest that disk failures occur independently of each other - which in reality is not always true, for example, disks from the same batch from one manufacturer may have similar defects. But for our approximate calculations will come down.
')
For now common sense prevails. It sounds reasonable, but unfortunately for many storage systems this does not work. In the article I will show why.
So easy to lose data, la la laaa
If your database cluster really consists of only three machines, then the probability of simultaneous failure of all three is really very small (except for correlated failures, such as a fire in the data center). However, if you switch to larger clusters, the probabilities change. The more nodes and disks in your cluster, the greater the likelihood of data loss.
This is a counterintuitive idea. “Of course,” you think, “each piece of data is still replicated on three disks. The probability of a disk failure does not depend on the cluster size. So why does cluster size matter? ”But I calculated the probabilities and drew a graph that looks like this:

For clarity, not the probability of failure of one node is indicated here, but the probability of irreversible loss of three replicas of some piece of data, so restoring from a backup (if you have one) will remain the only way to recover data. The larger the cluster, the more likely the loss of data. Probably, you did not expect this when you decided to pay for the replication factor 3.
In this graph, the y-axis is slightly arbitrary and depends on many assumptions, but the very direction of the graph is frightening. If we assume that a node has a 0.1% failure rate for a certain period of time, the graph shows that in a cluster of 8000 nodes, the chance of irreversible loss of all three replicas for some piece of data (for the same period of time) is about 0.2%. Yes, you read it correctly: the risk of losing all three copies of the data is almost twice as high as the risk of losing one node! What then is the meaning of replication?
Intuitively, this graph can be interpreted as follows: in a cluster of 8000 nodes, almost certainly several nodes are always dead at each moment of time. This is normal and not a problem: a certain level of failures and replacement of nodes was assumed as part of routine maintenance. But if you are unlucky, then there is a piece of data for which all three replicas were included in the number of those nodes that are now dead - and if this happened, then your data is lost forever. Lost data makes up only a small part of the entire data set in a cluster, but this is still bad news, because when using replication factor 3 you usually think “I don’t want to lose data at all” rather than “I don’t care about occasional loss of a small amount of data there are few of them. ” Maybe this particular piece of lost data is really important information.
The probability that all three replicas belong to the number of dead nodes is crucially dependent on the algorithm that the system uses to distribute data among replicas. The graph at the top is calculated with the assumption that the data is divided into sections (shards), and each section is stored on three randomly selected nodes (or pseudo-randomly with a hash function). This is a case of sequential hashing , which is used in Cassandra and Riak, among others (as far as I know). I'm not sure how the replica assignment works in other systems, so I will be grateful for the hints of those who know the features of the various storage systems.
Calculate the probability of data loss
Let me show you how I calculated the top graph using a probabilistic model of a replicated database.
Suppose that the probability of losing an individual node is . We ignore the time in this model, and just look at the probability of failure in some arbitrary period of time. For example, it may assume that - This is the probability of a node failing on a certain day, which makes sense if it takes about one day to replace the node and restore the lost data to new disks. For simplicity, I will not distinguish between a node failure and a disk failure , but I will take into account only irreversible failures (ignoring failures when the node returns to operation after a reboot).
Let be will be the number of nodes in the cluster. Then the probability that of the node has failed (assuming that the failures are independent of each other) corresponds to the binomial distribution :
Member - this is the probability that node failed member - the probability that the remaining remained in service, and - is the number of different ways to choose of nod. interpreted as the number of combinations of by . This binomial coefficient is calculated as:
Let be will be a replication factor (usually ). Assuming that of node failed, what is the probability that a particular partition has all your replicas on failed nodes?
Well, in a system with sequential hashing, each partition is assigned to the nodes in an independent and random (or pseudo-random) manner. For this section there is different ways to assign replicas of nodes, and all of these assignments can happen with the same probability. Moreover, there is different ways to choose replicas of failed nodes are ways in which all replicas can be assigned to failed nodes. Now let's calculate the part of the assignments that leads to the failure of all replicas:
(The vertical bar after “partition lost” means “under condition” and indicates a conditional probability : the probability is given under the assumption that node failed).
So, here is the chance that all replicas of one particular partition are lost. What about cluster with sections? If one or more partitions are lost, we lose data. Therefore, in order not to lose data, it is necessary that all sections were not lost:
Cassandra and Riak refer to sections as vnodes, but this is the same. In general, the number of sections does not depend on the number of nodes . In the case of Cassandra, there is usually a fixed number of sections on the node ; default (set by the
num_tokens parameter), and this is another assumption that I made for the graph above. In Riak, the number of partitions is fixed when creating a cluster , but usually the more nodes - the more partitions.Having collected everything in one place, we can now calculate the probability of losing one or more sections in a cluster of size with replication factor . If the number of failures less than the replication factor, then we can be sure that no data is lost. Therefore, you should add probabilities for all possible values by the number of failures. with :
This is a slightly excessive, but it seems to me an accurate assessment. And if you substitute , and and check the values from 3 to 10,000, then get a graph at the top. I wrote a small Ruby program for this calculation.
You can get a simpler approximation using the union boundary :
Even if the failure of one section is not independent of the failure of another section, this approximation is still applicable. And it seems that it quite closely corresponds to the exact result: on the graph, the probability of data loss looks like a straight line, proportional to the number of nodes.
The approximation says that this probability is proportional to the number of partitions, which is the same based on a fixed number of 256 partitions per node.
Moreover, if we substitute the number of 10,000 nodes in the approximation, we get which closely matches the output from the Ruby program.
But in practice ...?
Is this a problem in practice? I do not know. Basically, I think this is an interesting counterintuitive phenomenon. I heard rumors that this led to real data loss in companies with large clusters of databases, but I didn’t see the problem being documented somewhere. If you are aware of discussions on this topic, please show me.
Calculations show that to reduce the likelihood of data loss, reduce the number of partitions or increase the replication factor. Using more replicas costs money, so this is not the ideal solution for large clusters that are already expensive. However, changing the number of sections represents an interesting compromise. Cassandra initially used one partition per node, but a few years ago switched to 256 sections per node to achieve better load balancing and more efficient rebalancing. The reverse side, as can be seen from the calculations, was a much higher probability of losing at least one of the sections.
I think it is possible to develop an algorithm for assigning replicas, in which the probability of data loss does not grow with the cluster size or at least does not grow so fast, but where at the same time the properties of a good load distribution and balance recovery are preserved. This would be an interesting area for further research. In this context, my colleague Stefan noticed that the expected rate of data loss remains unchanged in a cluster of a certain size, regardless of the replica assignment algorithm — in other words, you can choose between a high probability of losing small amounts of data and a low probability of losing large amounts of data! Do you think the second option is better?
You need really large clusters before this effect really manifests itself, but clusters of thousands of nodes are used in different large companies, so it would be interesting to hear people with experience on this scale. If the probability of irreversible data loss in a cluster of 10,000 nodes is indeed 0.25% per day, this means a 60% chance of data loss per year. This is much more than the chance of “one in a billion” to die-from an asteroid, which I mentioned at the beginning.
Are architects of distributed data systems aware of the problem? If I understand correctly, here something should be considered when designing replication schemes. Perhaps this post will draw attention to the fact that just having three replicas does not make you feel safe.
Source: https://habr.com/ru/post/325216/
All Articles