Recommender systems in online education. Adaptive learning
Less than six months, as we complete a series of articles on adaptive learning on Stepik! And, no, it's gone ... But I am glad to finally present to your attention the final article on why adaptive learning is needed at all, how it is implemented at Stepik and what’s more, chess is here.

Introduction
Once we decided to tell on Habré how the system of adaptive recommendations on Stepik.org is arranged. The first two articles of this cycle were written in the hot summer months after my bachelor’s degree in mathematics at St. Petersburg State University, the first was generally about recommender systems in online education, the second we looked under the hood and told us about the architecture of our recommender system. The third part, in which we finally get to the adaptive recommendations, was written poorly, largely because this part of the platform is changing very quickly. But now I am ready to publish it.
Why do we need adaptability?
When they talk about the benefits of online learning, they often mention mass character. Indeed, it is difficult to compare the bandwidth of a full-time course at a university, even if it is streaming, and a massive online course that has virtually no limits for scaling - the difference in the size of the audience will be orders of magnitude.
But this feature is also a disadvantage of online education: in the case of classes in the classroom, the teacher can adjust his lectures to students: conduct a survey at the beginning of the semester, follow the lessons, do everyone understand the material, even communicate with individual students personally, if they they have not learned or, on the contrary, want to delve more into some topics. Of course, in the case of a massive online course, the teacher’s resources for such interaction are not enough, and the students find themselves in the strict framework of a linearly structured course without being able to analyze complex tasks in more detail or skip simple ones.
However, there are ways to implement something similar in automatic (mass) mode. These methods can be divided into three main groups:
- Differentiated learning. The easiest way to fine-tune the material to the student’s level of knowledge: the teacher creates several fixed learning trajectories of different complexity in advance, and the student chooses a suitable one for himself and then learns it in the usual, linear mode. For example, a series of textbooks for different levels of language skills.

- Personalized learning. In this case, the trajectory is built in the learning process, depending on the results of the student in the intermediate tests. The rules about when to test and what to advise to study further with different results, the teacher sets in advance. Something similar to a decision tree is obtained, according to which students will go differently depending on their success, but the tree itself must be thought out and created by the teacher.
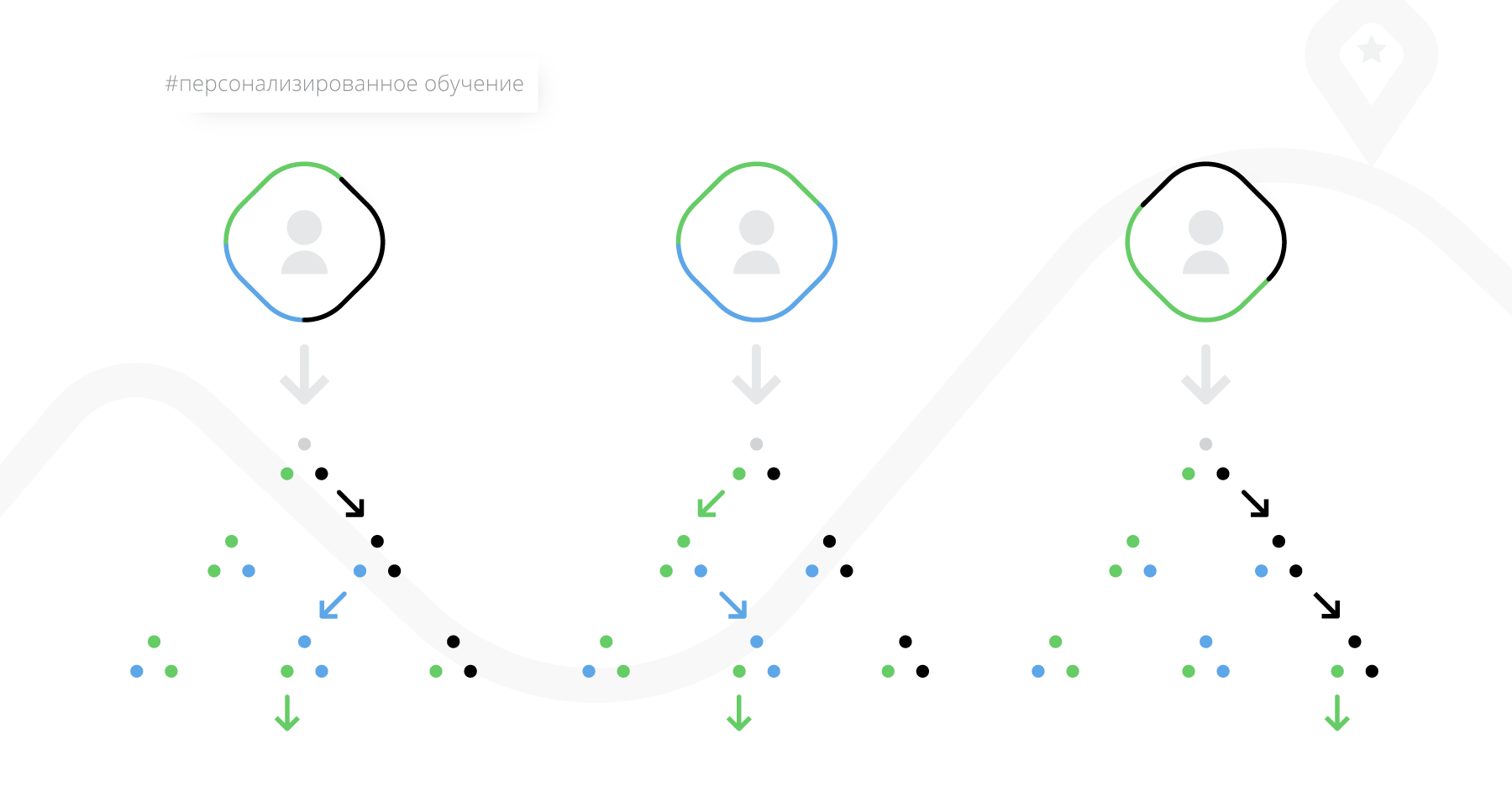
- Adaptive learning. The most interesting in terms of algorithms group. The trajectory is also built in the learning process, but does not require an initial markup from the teacher, but uses as much information as possible about how the student studies the material and how this material was studied before it. Further in article about it it will be told in more detail.
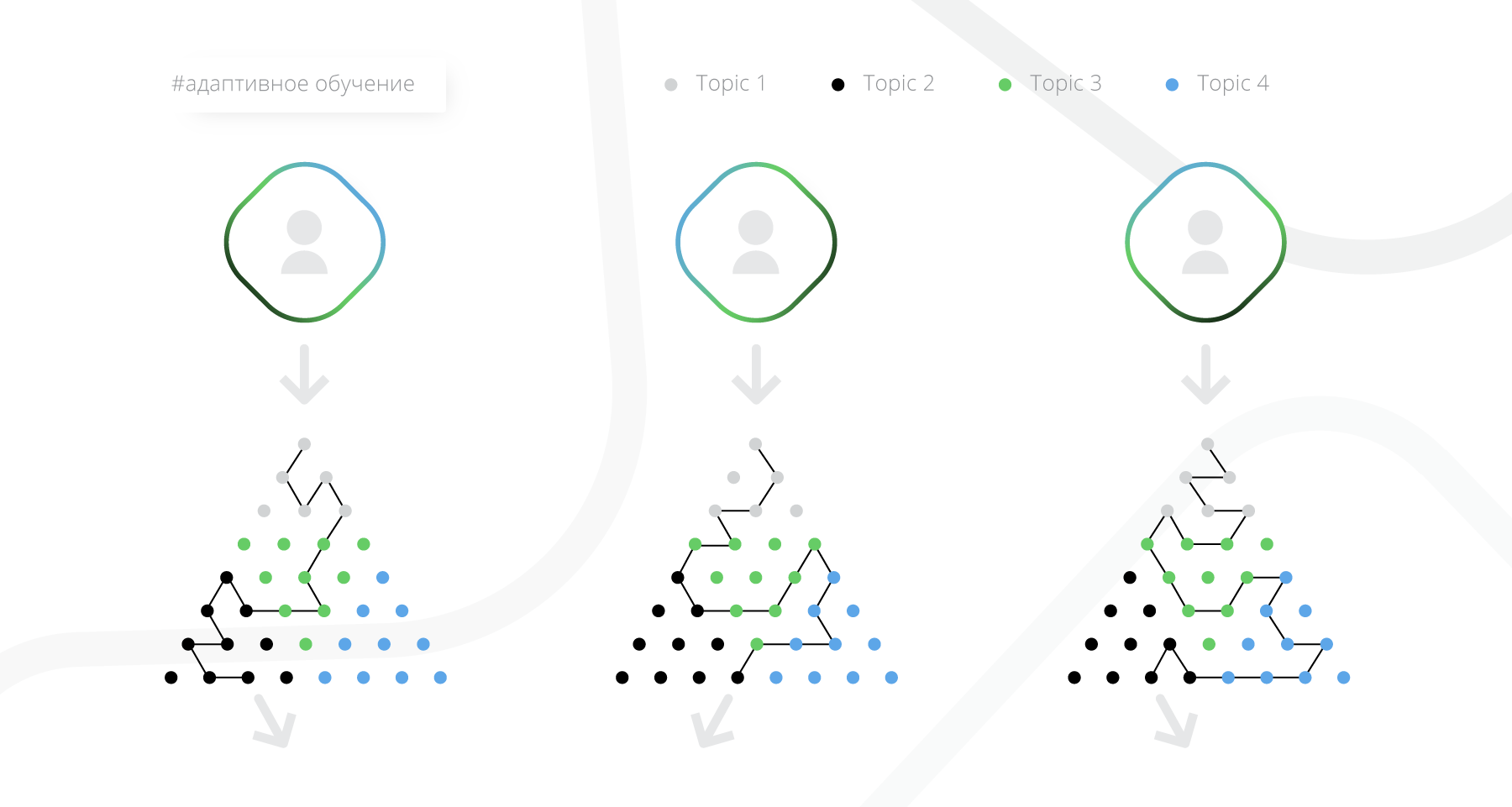
Adaptive learning mechanisms
Adaptive learning in Stepik is made in the form of a recommendation system, which advises the user what kind of lesson he should learn next, depending on his previous actions. So far, recommendations are made within the materials of the chosen course (for example, a Python simulator ), but in the near future, recommendations on an arbitrary topic (for example, C ++ or integrals) will also be available. In the future, any topic can be explored in adaptive mode.
For a registered user, to start learning in adaptive mode, simply click the “Learn” button in the adaptive course (it will become available after enrolling in the course).
Having received the material recommended for training (lesson), the user can respond to it in one of three ways:
- pass a lesson (solve problems in it),
- mark the lesson as too simple
- mark a lesson as too complicated.
After receiving the reaction, information about the user's knowledge and the lesson’s complexity is updated, and the user receives a new recommendation.
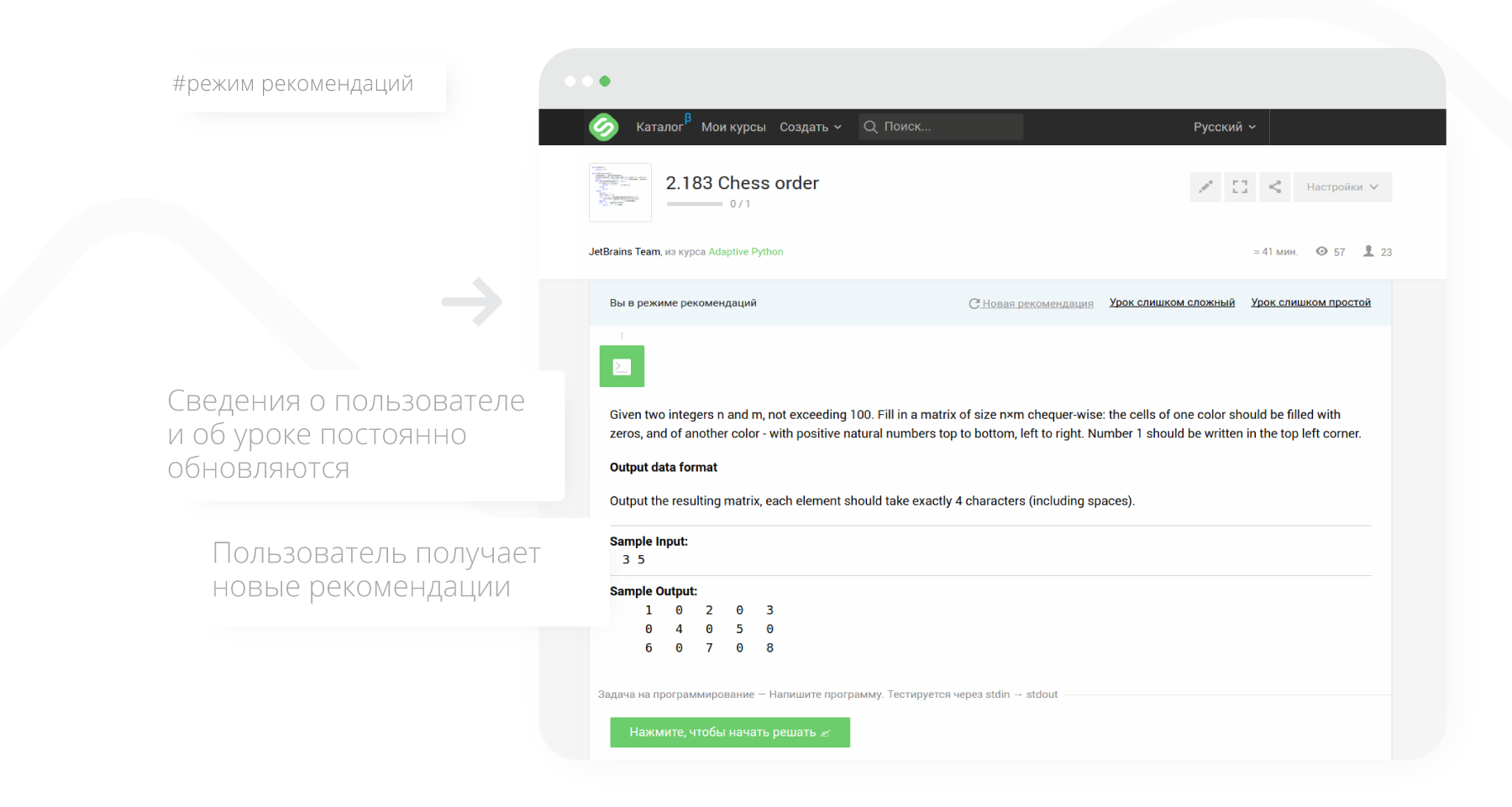
For adaptive recommendations, there are two methods (“handlers”): based on complexity and based on dependencies between topics (for more information on handlers, see the second article of the cycle ).
Under the hood of recommendations based on complexity are two ideas:
- Item Response Theory . This psychometric paradigm with a name that cannot be translated into Russian can be formulated very simply: the probability that a student will solve a problem is expressed as a certain function of the parameters of the student and the task. As parameters, you can use, for example, a somehow calculated level of user knowledge and complexity of the task, as well as how confident we are about these values.
- Elo chess rating. The model for assessing the rating of chess players, developed by Arpad Elo in the 1960s, works as follows: each new player is assigned a default rating (for example, zero), and then after each game, the ratings of both players are updated. To do this, we first calculate the expectation of the result of the game for each of the players ( in case of losing player A, - in case of victory, - draws), and then the ratings are updated depending on the difference between the predicted result of the game and the actual.
Formula to predict the result ,
for rating update ,
Where , - ratings of players A and B, - updated player rating A, - the actual result of the game for player A. Ratio characterizes our confidence in rating rating: if we still know little about a player, his rating should change quickly, but when it comes to an experienced master, one game, far from prediction, should not greatly change the rating.
As a result of the merging of these two ideas, we obtain the following model of the system. We consider users and lessons as “players”, the user’s reaction to the lesson’s recommendation as the result of a “game”, and we predict this result based on some parameters of the student and the lesson. We took the main features of this model from a scientific article about Maths Garden , a service for studying arithmetic for children. For the recommendation we select such a lesson, the probability of deciding which is close to optimal for the user.
In addition to the complexity of the lessons, we also want to take into account content marking with themes. We use the knowledge graph from Wikidata , and enable the lesson authors to tag them with two types of topics:
- the topics to which this lesson relates (which are explained in it),
- topics whose knowledge is necessary to understand this lesson.
For example, in case a user has marked a lesson as too complex, we can advise him to study the topics that are necessary for this lesson.
Metrics
The main metrics for assessing the quality of adaptive recommendations are, firstly, the proportion of decided lessons in the number of recommended (essentially retention), and secondly, the difference between the predicted outcome of the decision and the real one (from a model based on a chess rating).
The share of solved lessons speaks more about how helpful and appropriate in complexity users find the recommendations. We calculate this metric regularly on the basis of the results of the last 7 days, and since the end of last year it has grown from 60 to 80 percent.
The second metric, the prediction error, rather characterizes the accuracy of the internal machinery of the adaptive system. At the same time, it is more difficult to interpret, because changing models to predict the user's reaction and to assess the actual user behavior, we can get significant changes in this metric, which are unlikely to show whether the model has become better or worse compared to the previous version. Because we estimate the error, we now also differently.
For example, if before the values predicted_score and real_score were in the interval , and in the new version - in , the absolute values of the error will increase dramatically, but this will not mean that you need to urgently roll back. Of course, the example is exaggerated, but such reasons for the change in the error must be taken into account when analyzing the metrics.
As I wrote, these two metrics are basic, but not exhaustive. We also monitor the state of the system by the number of requests for recommendations (on the order of several thousand per week), by the moving average of prediction errors over several days (helps to identify a tendency to improve or worsen, smoothing the peaks), by the processing time of the request for a new recommendation (well there is something to strive for :) ).
We also conduct A / B testing to compare the work of different models. Then, in addition to the above metrics for daily monitoring, dashboards can be extended with specific metrics for a specific experiment. However, the decision on which model to leave is usually taken on the basis of basic metrics.
Adaptive Project History
- March 1, 2016 - the first prototype of adaptive recommendations appeared in Stepik (which in those days was also called Stepic)
- March 21, 2016 - the beginning of beta testing (Russian language problem book on Python)
- August 11, 2016 - integration of an adaptive system into PyCharm Edu 3 , a tool for learning Python from JetBrains
- September 2016 - the peak of user activity due to the fact that for attaining a certain level of “adaptive” knowledge in Python, a discount was given to programming training in the online program of the Computer Science Center and the Academic University. Fixed some funny bugs.
- December 2016 - March 2017 - competition for the creation of responsive content , which we have already written in detail on Habré .
The table below lists the main adaptive courses on Stepik and some information about their use.
| Course | Lessons | Students | Reactions to lessons |
|---|---|---|---|
| Adaptive Python | 382 | 1874 | 22904 |
| Python Adaptive Simulator | 55 | 2298 | 20546 |
| Pokemon! Gotta Catch 'Em All | 101 | 243 | 7661 |
| Adaptive GMAT Data Sufficiency Problems | 265 | 29 | 94 |
| Traffic Rules 2017 | 800 | 560 | 17649 |
Conclusion
In this article, I talked about the general features of the system of adaptive recommendations on the Stepik platform. Much remains behind the frame: how we predict the result of the student’s decision of the material, how we assess the real behavior, and also how we update the assessment of user knowledge and lesson complexity. Perhaps once on Habrahabr articles and about it, but now these parts of the system are changing faster than they can manage to describe.
However, I hope you were interested in reading this article. I will be glad to answer your questions in the comments or in personal messages.
')
Source: https://habr.com/ru/post/325206/
All Articles