Technocup: results of the final round and task analysis

On March 5, the final round of the Technoclub took place - a programming contest for schoolchildren. This year, 3000 people took part in it, 400 of whom went to the final. We invite you to take a look at the final results and the analysis of tasks:
A. Andrew and socks
B. The meeting place cannot be changed
C. Andryusha and colorful balls
D. Innokenty and the football league
E. Underground laboratory
F. Axel and Marston in Beatland
G. Andrew and the living barriers
H. Buses and Intranet
What is Technocup? This is a programming contest for students in grades 8-11, organized by the Mail.Ru Group together with the MGTU. Bauman and MIPT. It consists of three stages: trial (online), qualifying (online) and final (in-person).
Introductory rounds - online rounds for exploring the Codeforces platform. They are invited to solve two simple tasks to understand the system. Such rounds are held before each qualifying round. Their results do not affect the final ranking in the competition grid.
Qualifying rounds - online rounds on the Codeforces platform. According to the results, the best programmers reach the final. At such rounds it is proposed to solve six problems. To get to the final stage, you must pass the selection of at least one of these rounds.
The final round is the internal stage of the Olympiad. It takes place in Moscow in March 2017 on the basis of MIPT and MSTU. Bauman. Participants are invited to solve problems on computers on the Codeforces platform.
Rewarding In 2017, the winners and prize-winners of Tekhnokubka receive, when they enroll in universities, the benefits of a third-level Olympiad, special conditions for admission to the Moscow Institute of Physics and Technology and the Moscow State Technical University. Bauman.
All participants in the intramural stage receive memorable prizes. Usually these are championship t-shirts. For the first three places there is also a valuable prize in the form of Apple equipment, and the winner is waiting for Technocup. The winners are awarded at the Mail.Ru Group office, where they can chat with the developers and see their jobs.

Tehnokubka winners 2017
In 2017, Alexandra Drozdova, Moscow, 11th grade student of SSC Moscow State University, won second place a year earlier, won the Technocup. On the second line in the list of leaders was Arthur Petukhovsky, Vitebsk, and on the third - Vladimir Romanov, Moscow. Full results can be found here . Congratulations to the winners!

Analysis of the tasks of the final round
The participants of the final were offered to solve 8 problems in 3 hours. The top three managed to cope with a family of them. Another 17 people overcame 6 tasks, and 32 people coped with 5 tasks.

A. Andrew and socks
Time limit per test - 2 seconds
Memory limit per test - 256 megabytes
Input - Standard Input
Output - Standard Output
Andryusha is a very neat and tidy boy, so he always keeps order in his room. In particular, he is very careful about putting his things in the closet.
Today, he faced a difficult task - to put socks in the cabinet. Andryusha has n different pairs of socks, which were originally bagged. Pairs of socks are numbered from 1 to n . Andrew wants to remove the socks in the closet in pairs. To do this, he one by one pulls out the socks from the bag, and for each pulled out sock it looks to see if he already took out a pair of it. If not, which means that the pair of current sock is still in the bag, then Andryusha puts the current sock on the table in front of him. Otherwise, he removes the current sock and his pair in the closet.
Andrew is very attentive, so he remembered the order in which he got his socks out of the bag. Now he wondered, and what was the maximum number of socks at the same time lying on the table in front of him? Help Andryusha to answer this question.
Input data
The first line contains a single integer n (1 ≤ n ≤ 10 5 ) - the number of pairs of socks.
The second line contains space-separated 2 n numbers x 1 , x 2 , ..., x 2 n (1 ≤ x i ≤ n ), which describe the order in which Andryusha took his socks out of the bag. Namely, the number x i means that the i -th in order Andryusha got a sock from the pair x i .
It is guaranteed that Andryusha got exactly two socks from each pair.
Output
In a single line print one number - the maximum number of socks that have ever been on the table in front of Andrew.
Examples
Input data
one
eleven
Output
one
Input data
3
2 1 1 3 2 3
Output
2
Note
In the first example of the condition, Andryusha takes a sock out of the bag from the first pair and puts it on the table. Then he pulls out the next sock, which is also from the first pair, so he immediately takes both socks and puts them in the closet. Thus, a maximum of one sock lay on the table.
Consider what happens in the second example:
- At first there is nothing on the table, Andryusha gets a sock out of the pair number 2.
- On the table lies a sock (2). Andrew pulls out a sock from a pair of number 1 and puts it on the table.
- On the table are socks (1, 2). Andrew pulls out a sock from a pair of number 1, but such a sock is already on the table. Therefore, Andryusha removes both socks in the closet.
- On the table lies a sock (2). Andrew pulls out a sock from a pair of number 3 and puts it on the table.
- Socks are on the table (2, 3). Andryusha pulls out a sock from pair number 2, but such a sock is already on the table. Therefore, Andryusha removes both socks in the closet.
- On the table lies a sock (3). Andrew pulls out a sock from a pair of number 3, but such a sock is already on the table. Therefore, Andryusha removes both socks in the closet.
Thus, on the table at a time lay a maximum of two socks.
Simple task to implement. We will keep in the array whether the sock of each type is on the table, we will also store the number of socks and the largest value of this number. Now we will process the socks one by one and update all the necessary values.
Difficulty: O ( n ) time and memory.
B. The meeting place cannot be changed
Time limit per test - 5 seconds
Memory limit per test - 256 megabytes
Input - Standard Input
Output - Standard Output
The main street in Baytsiti has the appearance of a long straight line from south to north. For convenience of orientation on a straight line, the coordinates are entered, measured in meters from the southernmost house towards the north.
In some points of the street there are now n friends, and the i- th of them is located at the point with the coordinate x i meters and can move with a maximum speed of v i meters per second in either of two directions along the street - to the south or to the north.
You have the task to determine the minimum time during which all n friends can meet at one point on the main street. Note that the point where friends will meet is not required to have an integer coordinate.
Input data
The first line contains a single integer n (2 ≤ n ≤ 60 000) - the number of friends.
The second line contains n integers x 1 , x 2 , ..., x n (1 ≤ x i ≤ 10 9 ) - the current coordinates of friends in meters.
The third line contains n integers v 1 , v 2 , ..., v n (1 ≤ v i ≤ 10 9 ) - the maximum speeds of friends in meters per second.
Output
Print the minimum time (in seconds) for which all n people can meet at one point.
Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6 . Formally, let your answer be a , and the jury's answer b . Your answer will be considered correct if .
Examples
Input data
3
7 1 3
1 2 1
Output
2.000000000000
Input data
four
5 10 3 2
2 3 2 4
Output
1.400000000000
Note
In the first example, all friends can meet at point 5 in 2 seconds. For this, the first friend must go all the time with his maximum speed to the south, and the second and third must go with their maximum speeds to the north.
We use the binary search for the answer. Inside a binary search, you need to check whether all friends can meet in t seconds. During this time, the i- th friend can be at any point of the segment [ x i - tv i , x i + tv i ]. For a meeting to be possible, some point must belong to all these segments, that is, their intersection must be non-empty.
A convenient way to intersect a set of segments [ l 1 , r 1 ], ..., [ l n , r n ] is to calculate L = max l i and R = min r i . If L ≤ R , then [ L , R ] is the desired intersection, otherwise the intersection is empty.
Complexity: time and O (n) memory. Here ε is the required relative error.
C. Andryusha and colorful balls
Time limit per test - 2 seconds
Memory limit per test - 256 megabytes
Input - Standard Input
Output - Standard Output
Andryusha walks through the city park every day since his childhood. The tracks and glades of the park all the time seemed to him too identical, and once he decided to decorate them and make them diverse.
The park consists of n glades, which are interconnected (n - 1) by two-way lanes, and from each glade you can walk along the paths to any other.
Andrew decided to hang one colored ball on each clearing. The colors of the balls are given by positive integers, starting from 1. To make the park more diverse, Andryusha decided to choose the colors of the balls in a special way. Namely, he wants to hang the balls so that for any three pair of different glades a , b and c such that a and b are connected by a track, and b and c are connected by a track, the colors of the balls on these fields are pairwise different.
In order not to spend a lot of money on the purchase of balls, Andryusha wants to use as few different colors as possible. Since Andryusha is not very good at programming, he asks you to help him solve this problem.
Input data
The first line contains a single integer n (3 ≤ n ≤ 2 • 10 5 ) - the number of glades in the park.
In each of the following ( n - 1) lines there are two integers x and y (1 ≤ x , y ≤ n ) - the numbers of the two meadows connected by the next track.
It is guaranteed that from any clearing you can get to any other paths.
Output
In the first line print a single integer k - the minimum number of colors that Andryusha needs to use.
In the second line print n integers, the i -th of which is equal to the color of the ball to be hung on the i- th clearing. Each of the numbers must be in the range from 1 to k .
Examples
Input data
3
2 3
13
Output
3
1 3 2
Input data
five
2 3
5 3
4 3
13
Output
five
1 3 2 5 4
Input data
five
2 1
3 2
4 3
5 4
Output
3
1 2 3 1 2
Note
In the first example, the condition of the park consists of three glades, which are connected in series: 1 → 3 → 2. This means that the colors of the balls on each meadow should be pairwise different.
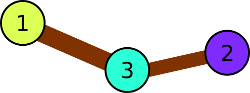
Illustration to the first example
In the second example in the park you can find the following triples of meadows connected in series:
- 1 → 3 → 2
- 1 → 3 → 4
- 1 → 3 → 5
- 2 → 3 → 4
- 2 → 3 → 5
- 4 → 3 → 5
From here we see that each pair of meadows lies in some kind of triplet, which means that the colors of the balls on all the glades should be different in pairs.

Illustration to the second example
In the third example there are the following triples:
- 1 → 2 → 3
- 2 → 3 → 4
- 3 → 4 → 5
This means that one or two colors is not enough, and for three colors the answer exists and is given in the example.
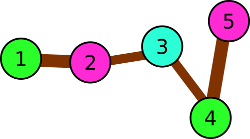
Illustration for the third example
If the vertex v has degree d , then the answer is at least d + 1. Indeed, any two neighbors v lie on a common path of length 3 passing through v . In addition, v lies on a common path of three vertices with any of its neighbors (possibly using non-neighbors). This means that v and all its neighbors must have pairs of different colors.
We show that this estimate is the best. Construct the coloring of the tree in D + 1 color, where D is the maximum degree of the vertex. We hang a tree by any vertex, after which we color the root and all its sons in colors 1, 2, and so on. The remaining vertices are colored according to the following rule: if the vertex v has the color x , and its parent has the color y , then the children v receive consecutive colors starting from 1 and skipping the colors x and y . It is easy to see that colors with numbers greater than D + 1 will never be needed.
From the point of view of implementation, this procedure is a usual detour in depth.
Difficulty: O ( n ) time and memory.
D. Innokenty and the football league
Time limit per test - 2 seconds
Memory limit per test - 256 megabytes
Input - Standard Input
Output - Standard Output
Innokenty is the president of the newly established football league in Byteland. The first task that he faces is to ensure the broadcast of all league matches on television. As you may know, during a football match, abbreviated names of teams and current scores are displayed on the screen. Of course, it will be strange if the abbreviated names of the clubs of the opponents match, so Innokentiy should figure out how to reduce the name of each of the league’s clubs to three letters so that all the teams of the league have different names.
The name of each club consists of two words: the name of the team and the city where the club is located, for example, “DINAMO BYTECITY”. Innocent does not want to distort the name, so he wants to choose an abbreviated name for each of the clubs in such a way that:
1) either the abbreviated name of the club coincided with the first three letters of the team name, for example, for the above command it is “DIN”,
2) either the first two letters of the abbreviated name of the club coincided with the first two letters of the team name, and the third with the first letter of the city of the team. For example, for the above command this is “DIB”.
In addition, if for some command x the second version of the name is chosen, then there should not be a command that has the first version of the abbreviated name, which coincides with the first version of the command name x . For example, if the abbreviated name of the above command is “DIB”, then no command that has the first version of the abbreviated name chosen should have the abbreviated name “DIN”. It is possible that some team will receive the name "DIN", where "DI" is the first two letters of the team name, and "N" is the first letter of the city. Of course, no two teams should have the same abbreviated name.
Help Innocent choose a short name for each of the teams. If this is not possible, report it. If there are several possible answers, Innocent will suit any of them. If for a certain team both versions of the abbreviated name are the same, then Innocent will still formally assume that only one of these options is chosen.
Input data
The first line contains a single integer n (1 ≤ n ≤ 1000) - the number of football clubs in the league.
Each of the next n lines contains two words - the name of the team and the name of the city of the next club. Both the name of the team and the name of the city consist of capital letters of the Latin alphabet and have a length of not less than 3 and not more than 20.
Output
If you choose abbreviated names that meet the requirements of Innocent, it is impossible to output a single line "NO".
Otherwise, print on the first line "YES". Then output n lines, in each line print the abbreviated name of the next club. Output the clubs in the order in which they are given in the input data.
If there are several possible answers, output any.
Examples
Input data
2
DINAMO BYTECITY
FOOTBALL MOSCOW
Output
YES
DIN
FOO
Input data
2
DINAMO BYTECITY
DINAMO BITECITY
Output
NO
Input data
3
PLAYFOOTBALL MOSCOW
PLAYVOLLEYBALL SPB
GOGO TECHNOCUP
Output
YES
PLM
Pls
Gog
Input data
3
ABC DEF
ABC EFG
ABD OOO
Output
YES
ABD
ABE
Abo
Note
In the first example, you can choose the first name option for both teams.
In the second example, it is impossible to choose names, since according to the condition it is impossible for one team to choose the first variant of the name, and for the second one to choose the second variant of the name, if the first variants of the names of these commands coincide.
In the third example, you can select the second name options for the first two teams, and the first option is for the third team.
In the fourth example, notice that it is permitted that the selected name of some command x matches the first version of the name y , if the first version of the name x does not match the first version of the name y .
We will denote a i and b i the first and second options for the name of the i-th club, respectively.
If all a i are different, we can use all of them as names. Otherwise, suppose that a i = a j for some clubs i and j , then they cannot be used simultaneously. In addition, to choose, for example, a i and b j in such a situation is also prohibited by the condition. It turns out that we have to choose b i and b j as names.
If now for some other club k we have a k = b i , then we should choose b k as its name. Such chain dependencies can be processed by any bypass algorithm. If at some point we are obliged to use the same names, then there is no solution, otherwise after resolving all the conflicts we will get the right solution.
Difficulty: O (n) time and memory with accurate implementation (in these limitations it was not necessary).
E. Underground laboratory
Time limit per test - 1 second
Memory limit per test - 256 megabytes
Input - Standard Input
Output - Standard Output
In a huge underground laboratory, the evil Umbrella Corporation creates clones for its terrible experiments. Once the company cloned a boy named Andryusha, who was smarter than his peers. Andrew realized that something was going on around the wrong. He raised clones to fight against the corporation, and they began to look for a way out of the laboratory. The company had no choice but to launch the process of self-destruction of the underground complex.
The laboratory is a connected graph of n vertices and m edges. In some vertices of this graph, k clones of Andryusha begin to search for a way out of the laboratory. In the process of searching, every second they go along the edge to the next vertex, and at each vertex there can be as many clones as you like. Each clone can stop and stop searching at some point in time, but it must start them, that is, visit at least one vertex. Moreover, the output can be in an arbitrary place in the laboratory, so the clones must bypass the entire graph, that is, each vertex of the graph must be visited at least one clone at least once.
The time of the clones is limited, and each of them can bypass no more rooms before the lab explodes.
Your task is to place the clones on the vertices of the graph and for each clone to bring the way in which he must bypass the graph. Moreover, the number of vertices in each path should be no more. .
Input data
The first line contains three integers n , m and k (1 ≤ n ≤ 2 • 10 5 , n - 1 ≤ m ≤ 2 • 10 5 , 1 ≤ k ≤ n ) - the number of vertices in the graph, the number of edges in the graph and number of clones.
Each of the next m lines contains two integers x i and y i (1 ≤ x i , y i ≤ n ) - the numbers of two vertices connected by the next edge. The graph may contain loops and multiple edges.
It is guaranteed that the graph is connected.
Output
Print k lines. At the beginning of the i- th line output an integer c i ( ) - the number of vertices that the i- th clone will visit, and then output c i integers - the numbers of the vertices that he will visit, in the order of their visit. Derive a vertex every time a clone visits her, even if he has visited it before.
It is guaranteed that the answer exists.
Examples
Input data
3 2 1
2 1
3 1
Output
3 2 1 3
Input data
5 4 2
12
13
14
15
Output
3 2 1 3
3 4 1 5
Note
In the first test there is only 1 clone, he visits the vertices in the order (2, 1, 3), which fits into the restriction of 6 visited vertices.
In the second test, there are 2 clones, they visit the vertices in the order (2, 1, 3) and (4, 1, 5), which fit into the limit of 5 visited vertices.
We will launch a deeper in depth from any vertex of the graph and write out the Eulerian detour - the order in which the detour visits the vertices, and the vertex v is written out every time the detour enters it, in particular, after each recursive call made from v . Note that the Eulerian round contains 2 n - 1 entries and is the correct answer for k = 1. For the general case of k , we cut the Eulerian round into k parts of size no more than ⌈ 2 n / k , and output these parts in response. Note that by the condition in each part there must be at least one vertex, therefore, it is necessary to add any vertex to the empty parts of the constructed answer.
Difficulty: O ( n + m ) time and memory.
F. Axel and Marston in Beatland
Time limit per test - 5 seconds
Memory limit per test - 256 megabytes
Input - Standard Input
Output - Standard Output
Two friends, Axel and Marston travel together around Bitlandia. There are n cities in Bitlandia, some pairs of which are connected by unidirectional roads. The roads in Beatland are pedestrian and cycling. In Bitlandia, there may be several roads between each pair of cities, and there are even roads from the city to it. However, no two roads in Bitland can have the same beginning, end and type at the same time.
Friends are in city 1 and want to draw up a travel route. Axel likes walking, and Marston prefers the bike. To make the route varied and interesting for each of the friends, they choose the order of alternation of the types of roads covered as follows:
- The route begins with a pedestrian road.
- Let the known beginning of the route be written as a string s of the letters P (pedestrian road) and B (bicycle road). Then a line is added to route s
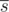 where
where  means the string s , in which the type of each road is replaced by the opposite (all pedestrian roads are cycling, and vice versa).
means the string s , in which the type of each road is replaced by the opposite (all pedestrian roads are cycling, and vice versa).
The first few steps of building a route will look like this: P, PVPVVPP, PVVPVPVVVVVPVPVVPPVPVVP, and so on.
Further, friends begin to move in city 1 along the roads of Bitlandia, each time choosing the type of the next road in accordance with the next symbol of the route. If it is not possible to choose a suitable road, the friends end their journey and fly home.
Help your friends determine the longest possible duration of their journey if they follow the constructed sequence of road types. If friends can find a path consisting of more than 10 18 roads, output -1 instead of the length.
Input data
The first line contains two integers n and m (1 ≤ n ≤ 500, 0 ≤ m ≤ 2 n 2 ) - the number of cities and roads in Bitlandia, respectively. The following m lines describe the roads. The i- th of these lines contains three integers v i , u i and t i (1 ≤ v i , u i ≤ n , 0 ≤ t i ≤ 1), where v i and u i are the numbers of the cities that are the beginning and the end of the i- th road, and t i specifies the type of the i -th road (0 - pedestrian road, 1 - bicycle road). It is guaranteed that for each pair of different numbers i , j , such that 1 i , j ≤ m , either v i v v j , or u i ≠ u j , or t i t j .
Output
If the friends can find a suitable path of length strictly greater than 10 18 , print the single number -1. Otherwise, print the maximum length of a suitable path, that is, the greatest number of roads that friends can go.
Examples
Input data
2 2
1 2 0
2 2 1
Output
3
Input data
2 3
1 2 0
2 2 1
2 2 0
Output
-one
Note
In the first example, the path of length 3 can be obtained by passing once along road 1 from city 1 to city 2, and then twice along road 2 from city 2 to it.
In the second example, we can get a path of arbitrarily long length, first passing along road 1, and then choosing road 2 or 3, depending on the next type of road.
We will denote by A i the binary string, obtained by i repetitions of inversion and attribution, for example, A 0 = 0, A 1 = 01, etc. Also denote 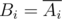 . By definition
. By definition 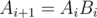 and
and 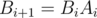 .
.
We calculate the matrices P k and Q k , the elements of P k / Q k ( v , u ) are equal to 1 for pairs of vertices v , u , such that from v to u there is a path corresponding to the line A k / B k . The matrices P 0 and Q 0 are obviously just adjacency matrices with 0 and 1 edges, respectively. Further, we note that P k + 1 ( v , u ) = 1 if and only if for some vertex w P k ( v , w ) = Q k ( w , u ) = 1 is fulfilled, and a similar criterion works for Q k + 1 ( v , u ). Thus, we can calculate P k + 1 and Q k + 1 using P k and Q k in O ( n 3 ) time (in fact, the recalculation consists in multiplying the bit matrices: 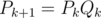 ,
,  ).
).
Now with the help of P k and Q k we find the answer. We will store the current maximal answer L , and the set of vertices S reachable from vertex 1 along some correct path of length L. We will iterate k in descending order from some value of k 0 , and check whether L can be increased by 2 k . After the L position, the next 2 k characters form the string A k or B k , depending on the parity of the number of ones in the bit record L. Let S ' be the set of vertices reachable from S along the path corresponding to Ak / Bk . If S 'is non-empty, increase L by 2 k , and assign S = S' , otherwise, we will not do anything. In the end, L will be the maximum path length if it is less than 2 k 0.
Take k 0 = 60, because we are not interested in the exact value of the answer, if it is greater than 2 60 . It turned out a solution in time  , . ,
, . , 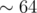 .
.
: 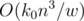
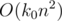 ,
, 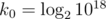 , w = 64 — .
, w = 64 — .
G.
— 4
— 256
—
—
. , , . w , 1 w , h , 1 h .
, . n , i - u i , l i r i . , . , , .
. , - . , , . , , . , - , . .

,
, , . , , . , i , , s i ( , u i + s i ), , . , , ( h + 1).
, . , . , 10 9 + 7.
h , w n (1 ≤ h ≤ 10 9 , 2 ≤ w ≤ 10 5 , 0 ≤ n ≤ 10 5 ) — , .
n . i - u i , l i , r i , s i (1 ≤ u i ≤ h , 1 ≤ l i ≤ r i ≤ w , 1 ≤ s i ≤ 10 9 ) — , i - . , , , . , , , , u i .
— 10 9 + 7.
10 5 1
3 2 3 10
7
10 5 2
3 1 3 10
5 3 5 10
sixteen
10 5 2
3 1 3 7
5 3 5 10
14
10 15 4
7 3 9 5
6 4 10 1
1 1 4 10
4 11 11 20
53
: , , — . 7.
2, 2, 4, 4, 4 .
1, 1, 4, 4, 4 . , , , , .
2, 2, 6, 6, 6, 6, 6, 6, 6, 1, 2, 1, 1, 1, 1 . , , .
1: . i - , y u i ≤ y ≤ u i + s i . x , .
, . ,  ; , . , , x , . , ( ) ; , ( , ).
; , . , , x , . , ( ) ; , ( , ). 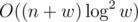 (
( std::set ).
2: , . - , . .
[ l , r ]. [ l , r ] , ( ) . w , . , [ l , r ], ( ). , . .
, O ( n + w ) , 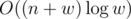 .
.
H.
— 10
— 256
—
—
In the town 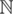 , , . m , ( ).
, , . m , ( ).
. T — , . 1 0, 2 — T / m , — 2 T / m , ..; , m ( m - 1) T / m . , ( , ) .
. D , D .
, . , , . 1 2, 2 3, .., , m 1.
, , D , .
n m (2 ≤ n , m ≤ 10 5 ) — .
n . x i , y i ( - 1000 ≤ x i , y i ≤ 1000) — .
, ( , ) . , . .
— . , 10 - 6 .
4 2
0 0
0 1
1 1
ten
1.000000000
2 2
0 0
ten
0.000000000
1 . , 0.5 1, D = 1.
, 0.5 (0.5, 0), D = 0.

,
. , , 1 2, 2 3, ..., n 1 x .
p ( t ) — 1 ( 0) t . t , || p ( t + T / m ) - p ( t )|| ≤ x , || a - b || a b . t , t , t + T / m , ..., t + ( m - 1) T / m , x .
p ( t + T / m ) - p ( t ) , , p ( t ) p ( t + T / m ). , p ( t + T / m ) - p ( t ) , . , - , O ( n ), O ( n ) .
t x . , . q = p ( t + T / m ) - p ( t ) || q || ≤ x , q . , , , . , . , q , .
, p ( t ), p ( t + T / m ), .. , [0, T ] m «» , . t — , m . — .
: 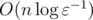 , ε — .
, ε — .
')
Source: https://habr.com/ru/post/325052/
All Articles