Java implementation of a hashed binary tree
One friend of mine likes to say (I don’t know if these are his words or he took them somewhere) that programmers go for two reasons: if you want to become a hacker or if you want to write games. My second case. Always interested in the development of games, and the part that is responsible for artificial intelligence in games. I spent a lot of time studying path finding algorithms. Implementing the next version of the A * algorithm in Java, I ran into an interesting situation related to the TreeSet and TreeMap collections.
Just want to introduce two concepts that I will use throughout the article: a search for equality and a search for comparison . I’ll search for equality in a search in a collection where the equals and hashCode methods are used to compare elements. Search by comparison or search based on the comparison I will call the search for an element in the collection, where the compare and compareTo methods are used to compare the elements.
The A * algorithm uses two collections to store waypoints: an open list and a closed list . The point of the path, roughly speaking, has three important attributes for us: the X coordinate, the Y coordinate, and the value of the metric function — F. For a closed list, only two addition and search operations are needed. With the open list, everything is somewhat more complicated. With an open list, in addition to the operations of adding and searching for an element, you must also find the smallest point by the value of the metric function.
For a closed list, choose HashSet, everything is obvious, for add and search operations, it is great, unless of course you have written a good hash function. There are difficulties with choosing a collection for an open list. If you select HashSet , as well as for the closed list, we get the best asymptotics for insert, search and delete operations - O (1), but the minimum search will be performed for O (n). When choosing a TreeSet or TreeMap, we will have O (log (n)) to insert and search, but to find and delete the minimum we will have the same O (log (n)). You can see the asymptotics of various collections here .
')
Another important detail associated with TreeMap and TreeSet is that all operations with these collections use comparisons. Thus, if we are interested in the search taking into account the coordinates of the points, then to find the minimum we use the value of the metric function, and this will lead to the fact that the operation may not be performed for the point at which this value was changed. Moreover, when inserting new values, we can get an incorrectly constructed tree: if we consider points with identical coordinates equal and take this into account in the comparator, then the insertion of a new value into the tree will not occur.
It makes sense to use a collection based on a binary tree, since elements are not added to the open list as often, while the search for the minimum element by the value of the metric function is performed at each iteration of the search algorithm. This is due to the fact that adding to an open list depends on the presence of a similar (by coordinates) element in a closed list, which grows over time and there are more and more points in it - the more points in a closed list, the less likely it is to add an element to an open list. list. But I would also like to have the advantages of the HashSet collection.
I decided to generalize the problem. Let some data structure be defined in which there is a set of fields. Let also some fields define the equivalence relation of two elements of a given structure, while other fields define order relations (in other words, the equals and hashCode methods use one object field, and the compare and compareTo methods use others).
Objective: to implement a data structure in which the operation of searching for an element based on equality is performed with the asymptotics O (1), and the insertion and deletion operations worked taking into account operations and comparison and equality, and built a binary tree so that the smallest element would be the root .
Since for my purposes I need to store the points in the open list, taking into account their coordinates, I can uniquely determine the hash function based on the size of the permeability map so that there are no collisions in it, so I decided in the collection to set the maximum number of elements .
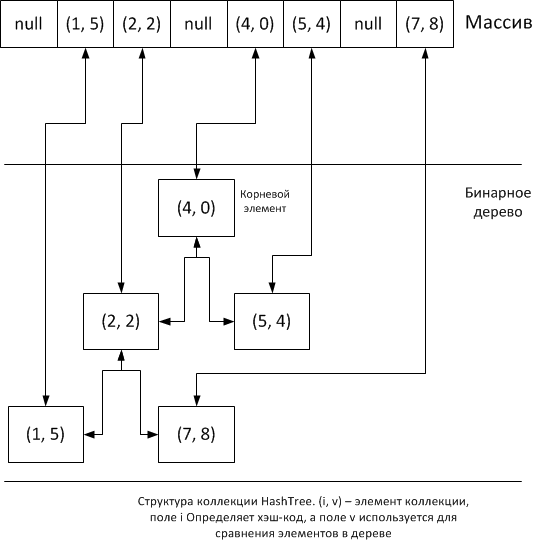
The idea is very simple: we will place the elements of the collection into an array on the basis of hashing, and immediately place the same elements in a binary tree. We need an inner class for packing items into tree nodes:
Type V defines a collection element, it must extend the Comparable class so that you can perform a comparison to build a tree.
In a class, in addition to pointers to the left and right descendant, there is a pointer to the ancestor. This is done to optimize the process of removing an item from the tree - having the progenitor of the item to be deleted can be excluded from the tree-by-root removal algorithm, you can use an array of items to search. A field named k contains the number of nodes in the subtree if they are not consecutively increasing nodes along the left descendant.
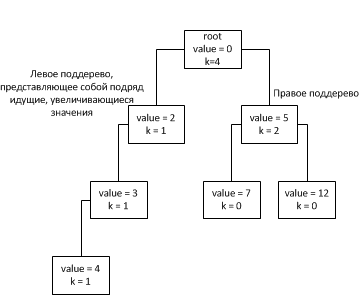
Inside the collection there should be a pointer to the root of the tree and an array of collection elements where null is stored in empty cells, and in the filled instances of the Node class, where the value of the added element (or more precisely, the value of the pointer to the object instance) will be stored in the data field:
Like type V, type E defines a collection element. By default, the collection is empty, so the pointer to the root element is null and the array is also filled with null values. An abstract class with the abstract getElementHash method that allows you to override the hash code calculation.
Now to the methods. AddElement method:
In the method we get the hash code of the added element. Create a new tree node with a new element as data and add it to the tree and to the array, where the hash code defines the index in the array. The insertion of an element into an array has the asymptotics O (1), the insertion into the tree is O (log (n)), the total asymptotics is O (log (n)).
RemoveElement method:
Here, using the hash code of the element to be deleted, the tree node to be deleted is extracted from the array. Using the ancestor of the node to be deleted, we perform the removal of the element, during which we have to cause subtree binding 2 times, each of the operations in the worst case has asymptotics - O (log (n)). As a result, the method has the asymptotics O (log (n)).
The connectNodes method performs the join of both a single node and a subtree. Moreover, the binding occurs with the use of comparison. Thus, at the top of the tree is always the smallest element.
ConnectNodes method:
The connectNodes method should be given special attention. Adding a new element is performed using this method in relation to the root and the new element. We assume that the tree is not empty:
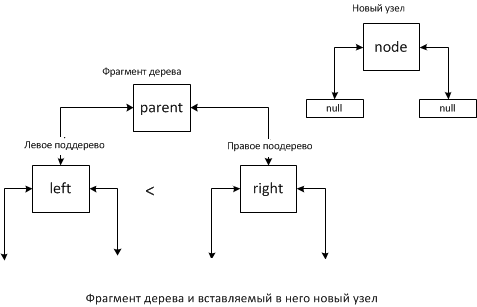
Perhaps 4 cases:
Case 1.
In this situation, parent becomes the left descendant of the new element, if parent is the root of the tree, then the new, added element will be the new root.
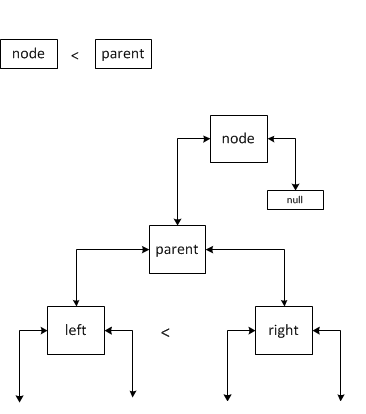
Case 2.
There are two possible options: the right descendant is defined and the right descendant is not defined. If the left descendant is not defined, then we consider that the left descendant has more significance the new node. In both situations, the new element becomes the left descendant of parent, and the left (which was the left descendant before adding) becomes the right descendant. However, in the second case, you must attach the old right descendant right to the new right descendant left. Joining left to right will occur according to the same rules as in the cases described.

Case 3.
In this case, either a transition is performed on the left subtree and a new node is added to it, if there are fewer nodes in it than in the right subtree, or the right subtree is replaced by the inserted node and the right subtree is added to it.
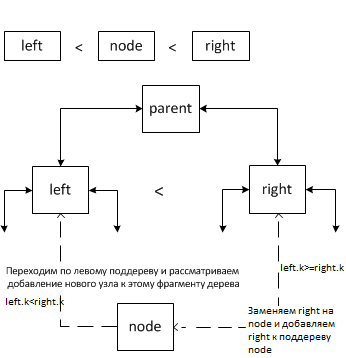
Case 4.
In this case, a transition is performed on the subtree in which there are the least nodes. The number of nodes accumulates in the k field.
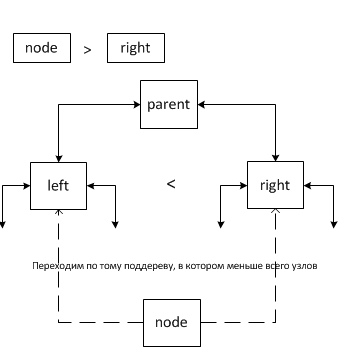
Now we estimate the asymptotics of the connectNodes method. In the best case, when nodes without descendants are added to the tree in decreasing order, the asymptotics will be equal to O (1), since in this case put the new element in the place of the progenitor. If we are talking about tying a node with descendants and a smaller one than the progenitor, then we will need to go through the node's subtree. For case 2 in paragraph a), the asymptotics is O (1), and in point b) one must again go through the subtree of the inserted node.
Note that the field k at the nodes increases for all cases except the 1st, this is done to fill the tree symmetrically, but not violating the increasing order in the left subtree if it meets.
To assess the difficulty of walking through a tree, it is enough to estimate its height. The height of the tree will be the desired asymptotics. A separate issue is the presence of a length sequence on the left subtree. Considering the presence of such subtrees, in the worst case, the asymptotic behavior of the binding can be considered as the asymptotic behavior of the binding to the subtree that we want to bind, and at best, as O (1) (2 case).
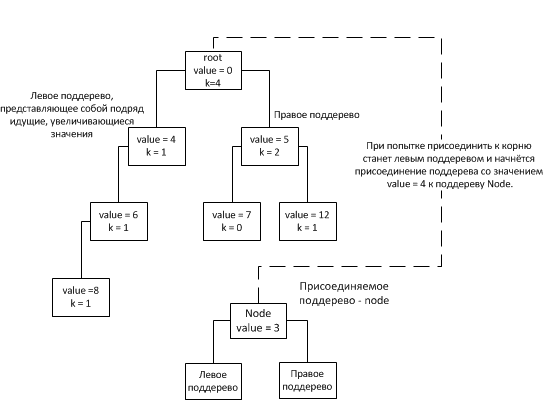
Since when we connect nodes we deal with nodes inside a tree, it means that the height of any subtree can be considered as not exceeding the height of the tree itself. Thus, estimating the height of the entire binary tree, we obtain the asymptotics of the connectNodes method. Due to the fact that the selection of a subtree for insertion is chosen based on the node's k field (in which the subtree size is stored, except for successive increasing nodes, they are counted as one node), the tree tends to fill its next level only after filling the previous one (excluding, of course, the above case 1). Thus, the tree will look like:
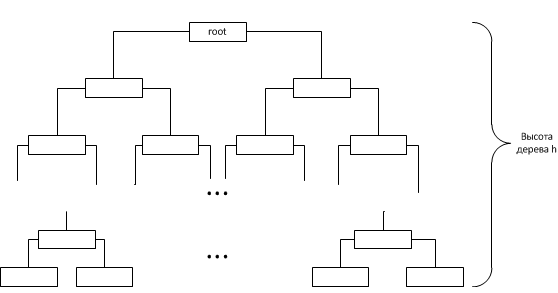
Thus, if n is the number of nodes in the tree, then . From which it follows that the height of the tree . It follows that the asymptotics of the connectNodes method is O (log (n)).
You can search for an element not in the tree, but in an array based on the hash code, so the search operation has the asymptotics O (1). And since the tree is organized as a binary, the minimum element is always at the root of the comparison and the asymptotics of the minimum search - O (1). I note that the removal of the minimum element has the asymptotic behavior of O (log (n)), since during the removal it is required to reorganize the tree, starting from the root using the connectNodes method.
At first glance, the operation of deleting the minimum element in the implemented collection has a worse asymptotics than the HashSet collection, but do not forget that before removing the minimum element, you must first find it, and this requires performing operations with the asymptotics O (n). Thus, the final asymptotics of the operation of deleting the minimum element in the HashSet collection will be O (n).
Checking the presence of an element in the collection, as mentioned above, is performed on the basis of checking for an array element null by its index determined by the hash code of the element. Verification is performed with the contains method and has the asymptotics O (1):
Also, based on the hash code, an equality search is performed with the same asymptotics using the getElement method:
The realized collection is not without flaws. It requires more memory, it needs a hash function without collisions, and to implement the iteration of the elements, it is necessary to implement a tree walk, which is also not fun, but this collection is intended for other purposes. The main advantage is the ability to search for elements of the same type according to different criteria with the best asymptotics. As applied to my task, it was a search for equality based on the coordinates and a search for the minimum element based on a comparison of the values of the metric function.
In the end, I’ll give the results of testing the collection for speed compared to the LinkedHashMap , TreeSet and HashSet collections. All collections were filled with 1000 values of type Integer and, with the collections filled, the following operations were performed:
The test results are shown in the table:
As a result, we have more than 2 times the speed of the HashTree collection compared to LinkedHashMap and 1.27 times faster than the TreeSet (there is no sense in considering HashSet at all). The checks were performed on a machine with 4GB of RAM and an AMD Phenom (tm) II X4 940 processor, the OS is 32-bit Windows7 Professional.
Just want to introduce two concepts that I will use throughout the article: a search for equality and a search for comparison . I’ll search for equality in a search in a collection where the equals and hashCode methods are used to compare elements. Search by comparison or search based on the comparison I will call the search for an element in the collection, where the compare and compareTo methods are used to compare the elements.
The A * algorithm uses two collections to store waypoints: an open list and a closed list . The point of the path, roughly speaking, has three important attributes for us: the X coordinate, the Y coordinate, and the value of the metric function — F. For a closed list, only two addition and search operations are needed. With the open list, everything is somewhat more complicated. With an open list, in addition to the operations of adding and searching for an element, you must also find the smallest point by the value of the metric function.
For a closed list, choose HashSet, everything is obvious, for add and search operations, it is great, unless of course you have written a good hash function. There are difficulties with choosing a collection for an open list. If you select HashSet , as well as for the closed list, we get the best asymptotics for insert, search and delete operations - O (1), but the minimum search will be performed for O (n). When choosing a TreeSet or TreeMap, we will have O (log (n)) to insert and search, but to find and delete the minimum we will have the same O (log (n)). You can see the asymptotics of various collections here .
')
Another important detail associated with TreeMap and TreeSet is that all operations with these collections use comparisons. Thus, if we are interested in the search taking into account the coordinates of the points, then to find the minimum we use the value of the metric function, and this will lead to the fact that the operation may not be performed for the point at which this value was changed. Moreover, when inserting new values, we can get an incorrectly constructed tree: if we consider points with identical coordinates equal and take this into account in the comparator, then the insertion of a new value into the tree will not occur.
It makes sense to use a collection based on a binary tree, since elements are not added to the open list as often, while the search for the minimum element by the value of the metric function is performed at each iteration of the search algorithm. This is due to the fact that adding to an open list depends on the presence of a similar (by coordinates) element in a closed list, which grows over time and there are more and more points in it - the more points in a closed list, the less likely it is to add an element to an open list. list. But I would also like to have the advantages of the HashSet collection.
I decided to generalize the problem. Let some data structure be defined in which there is a set of fields. Let also some fields define the equivalence relation of two elements of a given structure, while other fields define order relations (in other words, the equals and hashCode methods use one object field, and the compare and compareTo methods use others).
Objective: to implement a data structure in which the operation of searching for an element based on equality is performed with the asymptotics O (1), and the insertion and deletion operations worked taking into account operations and comparison and equality, and built a binary tree so that the smallest element would be the root .
Since for my purposes I need to store the points in the open list, taking into account their coordinates, I can uniquely determine the hash function based on the size of the permeability map so that there are no collisions in it, so I decided in the collection to set the maximum number of elements .

The idea is very simple: we will place the elements of the collection into an array on the basis of hashing, and immediately place the same elements in a binary tree. We need an inner class for packing items into tree nodes:
private static class Node<V extends Comparable<V>> { private Node parent; private Node left; private Node right; private int k = 0; private final V data; public Node(V data) { this.data = data; this.parent = null; this.left = null; this.right = null; } } Type V defines a collection element, it must extend the Comparable class so that you can perform a comparison to build a tree.
In a class, in addition to pointers to the left and right descendant, there is a pointer to the ancestor. This is done to optimize the process of removing an item from the tree - having the progenitor of the item to be deleted can be excluded from the tree-by-root removal algorithm, you can use an array of items to search. A field named k contains the number of nodes in the subtree if they are not consecutively increasing nodes along the left descendant.

Inside the collection there should be a pointer to the root of the tree and an array of collection elements where null is stored in empty cells, and in the filled instances of the Node class, where the value of the added element (or more precisely, the value of the pointer to the object instance) will be stored in the data field:
public abstract class HashTree<E extends Comparable<E>> { private Node root = null; private Node[] nodes; public HashTree(int capacity) { this.nodes = new Node[capacity]; } public abstract int getElementHash(E element); … } Like type V, type E defines a collection element. By default, the collection is empty, so the pointer to the root element is null and the array is also filled with null values. An abstract class with the abstract getElementHash method that allows you to override the hash code calculation.
Now to the methods. AddElement method:
public void addElement(E element) { int index = getElementHash(element); if (nodes[index] != null) { return; } Node<E> node = new Node<>(element); nodes[index] = node; this.root = connectNodes(this.root, node); } In the method we get the hash code of the added element. Create a new tree node with a new element as data and add it to the tree and to the array, where the hash code defines the index in the array. The insertion of an element into an array has the asymptotics O (1), the insertion into the tree is O (log (n)), the total asymptotics is O (log (n)).
RemoveElement method:
public E removeElement(E element) { int index = getElementHash(element); Node node = nodes[index]; if (node == null) { return null; } nodes[index] = null; E data = (E) node.data; Node l = getElemInArray(node.left); Node r = getElemInArray(node.right); if (l != null) { l.parent = null; } if (r != null) { r.parent = null; } l = connectNodes(l, r); if (node.parent == null) { this.root = l; if (this.root != null) { this.root.parent = null; } return data; } int p = getElementHash((E) node.parent.data); if (nodes[p] != null) {// , // , if (nodes[p].left == node) { nodes[p].left = null; } if (nodes[p].right == node) { nodes[p].right = null; } } connectNodes(nodes[p], l); return data; } Here, using the hash code of the element to be deleted, the tree node to be deleted is extracted from the array. Using the ancestor of the node to be deleted, we perform the removal of the element, during which we have to cause subtree binding 2 times, each of the operations in the worst case has asymptotics - O (log (n)). As a result, the method has the asymptotics O (log (n)).
The connectNodes method performs the join of both a single node and a subtree. Moreover, the binding occurs with the use of comparison. Thus, at the top of the tree is always the smallest element.
ConnectNodes method:
private Node connectNodes(Node parent, Node node) { if (node == null) { return parent; } if (parent == null) { return node; } else { if (compare(node, parent) < 0) { return connectNodes(node, parent); } Node cur = parent; Node n = node; while (cur != null) { if (cur.left == null) { cur.left = n; n.parent = cur; cur.k++; break; } if (cur.right == null) { if (compare(n, cur.left) <= 0) { cur.right = cur.left; cur.left = n; n.parent = cur; cur.k++; break; } else { cur.right = n; n.parent = cur; cur.k++; break; } } if (compare(n, cur.left) <= 0) { Node tmp = cur.left; cur.left = n; n.parent = cur; cur.k++; cur = n; n = tmp; continue; } if (compare(n, cur.right) < 0 && compare(n, cur.left) > 0) { cur.k++; if (cur.right.k < cur.left.k) { Node tmp = cur.right; cur.right = n; n.parent = cur; cur = n; n = tmp; } else { cur = cur.left; } continue; } if (compare(n, cur.left) > 0) { cur.k++; cur = cur.left.k < cur.right.k ? cur.left : cur.right; } } return parent; } The connectNodes method should be given special attention. Adding a new element is performed using this method in relation to the root and the new element. We assume that the tree is not empty:

Perhaps 4 cases:
- new element is smaller than the root;
- A new element is smaller than the left child;
- A new element is larger than the left child, but smaller than the right element.
- new item more right descendant.
Case 1.
In this situation, parent becomes the left descendant of the new element, if parent is the root of the tree, then the new, added element will be the new root.

Case 2.
There are two possible options: the right descendant is defined and the right descendant is not defined. If the left descendant is not defined, then we consider that the left descendant has more significance the new node. In both situations, the new element becomes the left descendant of parent, and the left (which was the left descendant before adding) becomes the right descendant. However, in the second case, you must attach the old right descendant right to the new right descendant left. Joining left to right will occur according to the same rules as in the cases described.

Case 3.
In this case, either a transition is performed on the left subtree and a new node is added to it, if there are fewer nodes in it than in the right subtree, or the right subtree is replaced by the inserted node and the right subtree is added to it.

Case 4.
In this case, a transition is performed on the subtree in which there are the least nodes. The number of nodes accumulates in the k field.

Now we estimate the asymptotics of the connectNodes method. In the best case, when nodes without descendants are added to the tree in decreasing order, the asymptotics will be equal to O (1), since in this case put the new element in the place of the progenitor. If we are talking about tying a node with descendants and a smaller one than the progenitor, then we will need to go through the node's subtree. For case 2 in paragraph a), the asymptotics is O (1), and in point b) one must again go through the subtree of the inserted node.
Note that the field k at the nodes increases for all cases except the 1st, this is done to fill the tree symmetrically, but not violating the increasing order in the left subtree if it meets.
To assess the difficulty of walking through a tree, it is enough to estimate its height. The height of the tree will be the desired asymptotics. A separate issue is the presence of a length sequence on the left subtree. Considering the presence of such subtrees, in the worst case, the asymptotic behavior of the binding can be considered as the asymptotic behavior of the binding to the subtree that we want to bind, and at best, as O (1) (2 case).

Since when we connect nodes we deal with nodes inside a tree, it means that the height of any subtree can be considered as not exceeding the height of the tree itself. Thus, estimating the height of the entire binary tree, we obtain the asymptotics of the connectNodes method. Due to the fact that the selection of a subtree for insertion is chosen based on the node's k field (in which the subtree size is stored, except for successive increasing nodes, they are counted as one node), the tree tends to fill its next level only after filling the previous one (excluding, of course, the above case 1). Thus, the tree will look like:

Thus, if n is the number of nodes in the tree, then . From which it follows that the height of the tree . It follows that the asymptotics of the connectNodes method is O (log (n)).
You can search for an element not in the tree, but in an array based on the hash code, so the search operation has the asymptotics O (1). And since the tree is organized as a binary, the minimum element is always at the root of the comparison and the asymptotics of the minimum search - O (1). I note that the removal of the minimum element has the asymptotic behavior of O (log (n)), since during the removal it is required to reorganize the tree, starting from the root using the connectNodes method.
At first glance, the operation of deleting the minimum element in the implemented collection has a worse asymptotics than the HashSet collection, but do not forget that before removing the minimum element, you must first find it, and this requires performing operations with the asymptotics O (n). Thus, the final asymptotics of the operation of deleting the minimum element in the HashSet collection will be O (n).
Checking the presence of an element in the collection, as mentioned above, is performed on the basis of checking for an array element null by its index determined by the hash code of the element. Verification is performed with the contains method and has the asymptotics O (1):
public boolean contains(E element) { int index = getElementHash(element); return nodes[index] != null; } Also, based on the hash code, an equality search is performed with the same asymptotics using the getElement method:
public E getElement(E element) { return (E) nodes[getElementHash(element)].data; } The realized collection is not without flaws. It requires more memory, it needs a hash function without collisions, and to implement the iteration of the elements, it is necessary to implement a tree walk, which is also not fun, but this collection is intended for other purposes. The main advantage is the ability to search for elements of the same type according to different criteria with the best asymptotics. As applied to my task, it was a search for equality based on the coordinates and a search for the minimum element based on a comparison of the values of the metric function.
In the end, I’ll give the results of testing the collection for speed compared to the LinkedHashMap , TreeSet and HashSet collections. All collections were filled with 1000 values of type Integer and, with the collections filled, the following operations were performed:
- placing a new item in the collection;
- checking for the presence in the collection of an element with a specified value (the check was performed twice for an element that was in the collection and for an element that was not in the collection);
- search and delete is minimal by comparing the item;
- deletion added in item 1 of the item.
The test results are shown in the table:
| Collection | Number of repetitions | Time spent |
|---|---|---|
| LinkedHashMap | 10,000,000 | 1985 ± 90 ms |
| Treeset | 10,000,000 | 1190 ± 25 ms |
| Hashset | 1,000,000 | 4350 ± 100 ms |
| Hashtree | 10,000,000 | 935 ± 25 ms |
As a result, we have more than 2 times the speed of the HashTree collection compared to LinkedHashMap and 1.27 times faster than the TreeSet (there is no sense in considering HashSet at all). The checks were performed on a machine with 4GB of RAM and an AMD Phenom (tm) II X4 940 processor, the OS is 32-bit Windows7 Professional.
Source: https://habr.com/ru/post/324988/
All Articles