Geekly Articles each Day
📜 ⬆️ ⬇️

Calculation of the correcting FIR filter on the FPGA



Hello! I was encouraged to write this article by speaking at seminars on digital signal processing, where students have always focused their interest in the method of calculating corrective FIR filters, despite the fact that I touched on this topic superficially and for the most part told about it in introductory features. If the public wants to get secret knowledge, then why not share it. In this article I will try to present in an accessible form an algorithm for calculating corrective FIR filters, which is necessary for equalizing the frequency response in the passband after the CIC filter links in the problems of decimation and interpolation of signals. In particular, consider the design of filters on modern FPGAs Xilinx. As usual, at the end of the article there will be a link to useful scripts for calculating various filters and getting a file of filter-corrector coefficients.

It is assumed that the reader is familiar with the basics of digital signal processing and has an understanding of CIC and FIR filters. Let's get started

Introduction


As is known, CIC filters are often used in problems of decimation and interpolation of signals, because they have one very important property - ease of implementation , which makes this class of filters cheap to perform. A special feature of CIC filters is the absence of multiplication operations for calculating the response at the filter output. CIC filters are applied everywhere, where work at several or different speeds is required, that is, in those tasks where decimation and interpolation of the data stream is required. Let me remind you that decimation refers to the process of lowering the signal sampling rate (reducing the data rate), and interpolation is the process of increasing the signal sampling rate (increasing the data rate). The CIC filter is an integral part of the DDC (Digital Down Converter) and DUC (Digital Up Converter) nodes.
')

The frequency response of the CIC filter is equivalent to the frequency response of the low-pass filter (LPF). The shape of the frequency response and the position of the zeros of the characteristics are influenced by some filter parameters: order- N , the decimation / interpolation coefficient — R , the delay value in the differentiating link — M. And it is precisely in the influence of these parameters on the FK that the main drawback of CIC filters lies. For large orders of the filter N and the values ​​of the decimation / interpolation coefficient R, the resulting spectrum in the passband deteriorates significantly, namely, the shape of the main lobe of the frequency response is distorted. For many multi-frequency and wideband signal processing tasks, it is necessary to have the most uniform and rectangular spectrum in the passband. But if you look at the graph of the frequency response of the CIC filter, then we see a sharply decreasing curve in the passband. Such unevenness is unacceptable and leads to the loss of energy of the useful signal and the distortion of its shape. In this regard, the urgent task of aligning the frequency response of CIC filters in the passband while minimizing interference in the attenuation band.

Formulation of the problem


Let there be a CIC filter for which the order of N and the rate of change of the sampling rate R are given . The delay value, if it is not a moving average filter, is in practice M = 1 or 2 and is determined by the registers at the nodes of the DSP48 FPGAs multipliers (regardless of the vendor, Altera or Xilinx). It is necessary to calculate the correction filter to equalize the frequency response after the signal passes through the CIC link of the filter.

Decision


The correction filter is easiest to do on the basis of the FIR filter. To calculate this filter, it is necessary to determine its parameters in advance:


The order is NFIR. This parameter defines the "quality" of the frequency response of the filter. The developer of DSP on the FPGA is constantly faced with the task of choosing the optimal order of the filter, because the greater the order is, the better in terms of frequency properties, but the more FPGA chip resources need to be spent to implement this filter. The optimal values ​​of the order of the filter-corrector are in the range from 32 to 128. In some tasks, the value of the order of the filter may be higher and reach the number 256, but in practice it does not make sense, and I have not seen such long filter-correctors. The correction filter should be small and not affect the computing resources that are needed to implement more complex things. The order of the filter for this implementation is better to set an even number and a multiple of a power of two, if we are talking about applying a FPGA-based filter, but this requirement is optional .

By effective bandwidth Fr, I mean the value of the relative normalized cutoff frequency after decimation or interpolation. For problems of decimation, it is calculated using the formula Fr = Fo / R , where Fo is the parameter of the normalized frequency (for example, from 0.1 to 0.5), and R is the decimation coefficient. The value of Fo determines the filter bandwidth. It should be noted that when Fr = 0.5, the order of the filter must be odd so that the zero frequency response of the filter-corrector does not fall into the band of the useful signal. For other values ​​of Fr, the filter order can be any. This is due to the peculiarities of calculating the FIR2 embedded function in Matlab CAD software.

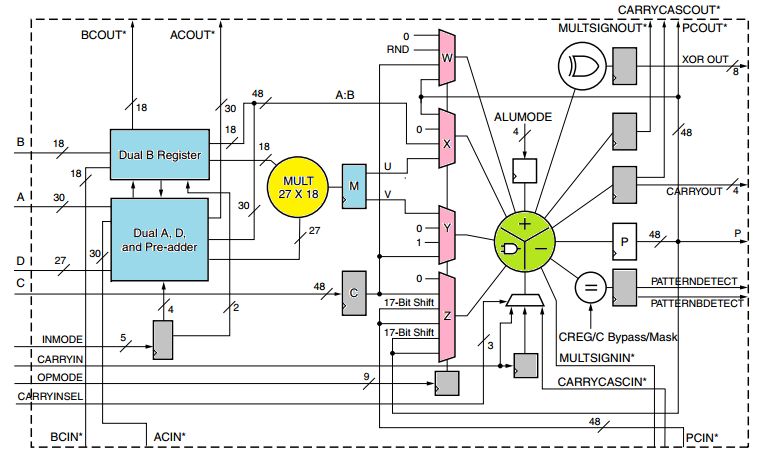
The width of the coefficients for the described algorithm determines the non-uniformity of the frequency response in the passband and the barrier line. In practice, the width of the coefficients is set from 16 to 27 bits, which is associated with the peculiarities of the DSP48 node of modern FPGAs. For practical purposes, it is enough to set the bit width of the coefficients equal to 16-18 bits and this will adequately ensure the required uniformity of the frequency response. For high-order filters (for example, N = 256), the bit width of 18 bits is insufficient and quantization effects begin to appear, in particular in the obstacle band. Therefore, for high-order filters, it is necessary to increase the width of the coefficients, since the structure of the DSP48 processing nodes in the FPGA allows for this (see fig. Of the DSP48 node).



Window filtering allows smoothing the pulsations of the resulting frequency response in the passband after applying the filter-corrector. The window function is superimposed on the impulse response of the calculated FIR filter (mathematically this is a convolution of the spectra). Based on personal experience, I note that the Kaiser function is the best version of the window function. Using one parameter BETA, you can change the frequency response of the filter for the desired task. The Kaiser function is calculated using the modified Bessel functions of zero order I0 , but in many standard packages it is built-in ( Matlab, GNU Octave, MathCAD ). Physically, the BETA parameter determines the fraction of energy concentrated within the main lobe of the spectrum. The larger the BETA parameter, the more concentrated the energy and the wider the main lobe, but the lower the side lobes level. For practical purposes, the parameter BETA = 3-11.

I will not give a detailed method for calculating the FIR filter, you can read about it in my previous article . There is nothing complicated - you need to get the FIR filter coefficients in any convenient way. This can be done using MathCAD, GNU Octave, Matlab (FDATool utility), ScopeFIR application, LabView program, or write your own calculation methodology based on known algorithms.

Algorithm


We describe the algorithm for calculating the corrective FIR filter. Below, Matlab script code inserts will be used to better understand the implementation process.

Step 1: set the initial parameters of the CIC filter -

R = 8; % Decimation factor N = 4; % Number of stages M = 1; % Differential delay (only 1)

Step 2: we set the parameters of the FIR filter (coefficient width, order, window) and the normalized cutoff frequency of the frequency response -

 NFIR = 128; % Filter order, must be odd when Fo = 0.5 ! Bc = 16; % Coef. Bit-width Fo = 0.3; % Normalized Cutoff: 0.2 < Fo < 0.5; BETA = 8; % BETA parameter for Kaiser window (if IS_WIND = 'Y')

Step 3: Select the step of "discretization" of vectors to calculate the characteristics. In accordance with this step, we create the required arrays of numbers. We calculate the CIC filter using a well-known formula and translate the result into decibels.

 HCIC = (R^-N*abs(1*M*sin(pi*M*R*ff) ./ sin(pi*ff)).^N); HCICdb = 20 * log10(abs(HCIC));

Step 4: In accordance with the effective bandwidth parameter Fo, we divide the frequency sample vector into two parts: fp is the frequency vector in the passband, fs is the frequency vector in the attenuation band. We calculate the ideal characteristic of the compensating filter with the cut-off frequency Fo / R according to the following formula:


where f - samples of the normalized frequency in the bandwidth range from 0 to Fo / R. The remaining counts are zero.

 % Calculate ideal response Mp = ones(1, length(fp)); % Pass band response; Mp(1) = 1 Mp(2:end) = abs(M * R * sin(pi*fp(2:end)/R) ./ sin(pi*M*fp(2:end))).^(N); Mf = [Mp zeros(1, length(fs))];

The type of the obtained characteristic is shown in the figure below:


Step 5: According to the ideal frequency response, we calculate the impulse response of the FIR compensating filter with the specified parameters (weight window, if any, coefficient width and filter order).

The type of the impulse response of the filter-corrector (the calculation is performed using the built-in function FIR2 , and the window function is calculated through the function FIR1 ):


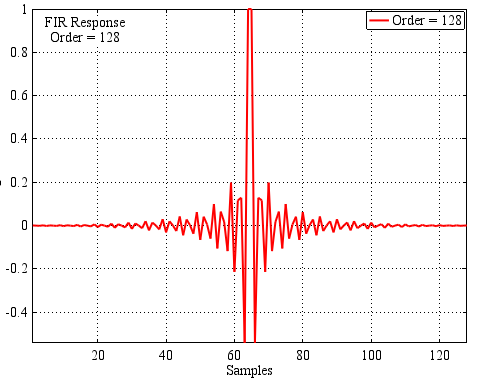
Source code for the calculation of their correction filter:

 % Calculate FIR hFIR = fir2(NFIR-1, f, Mf); % Filter length NFIR hFIR = hFIR / max(hFIR); % Double coefficients hCOE = round(hFIR*(2^(Bc-1)-1)); % Fixed point coefficients % Windowed FIR (Kaiser with BETA) if (IS_WIND == 'Y') WIND = kaiser(NFIR, BETA); % KAISER WINDOW IS USED! hWIND = fir1(NFIR-1, Fo/R, 'low', WIND); hNEW = hCOE .* hWIND;% conv2(hCOE,Hwind); hCOE = hNEW; end

At this point, the filter calculation ends. The result is a file of filter coefficients in a user-friendly form. As you can see, there is nothing complicated and the whole process is divided into 4-5 stages:


It should be noted that for downsampling schemes (decimation task), compensating filters are usually placed after CIC filters. For the tasks of increasing the sampling rate (interpolation), compensating filters are up to CIC filters. This arrangement of filters is best suited from the point of view of the amount of crystal resources occupied, since the corrective FIR filter in this case operates at a lower frequency (after decimation or before interpolation).

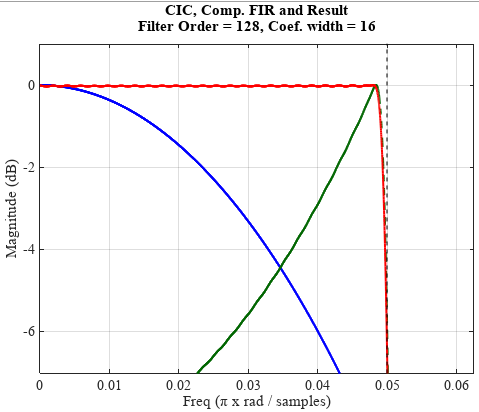
The following figure shows the frequency response of the CIC and FIR filters and the resulting frequency response after compensation with the following parameters:




As can be seen, the frequency response of the CIC filter is compensated, and the resulting frequency response visually has sufficient squareness (red curve).

Uneven frequency response in the passband


Unfortunately, the alignment of the frequency response does not end there. Increase the graph within the bandwidth. In the following graph you can see small beats in the band.


Why is that? The uneven frequency response in the passband is the higher, the greater the order of the CIC filter N. The decimation / interpolation coefficient R does not affect the non-uniformity. Also, non-uniformity is affected by the order of the compensating FIR filter. The smaller the filter order, the greater the unevenness. But the greater the order of the filter, the greater the frequency of "beats" in the passband. For this reason, for practical purposes, NFIR> 128 high-order compensating filters are not used! The effective band also makes a minor contribution: the smaller the strip being leveled, the smaller the unevenness.

To combat beats are used window functions, which I mentioned earlier. Let's see how the graph looks at an enlarged scale without window filtering and using the Kaiser function ( BETA = 8 ). The remaining parameters remain unchanged.



As you can see, window filtering allows you to smooth out the beats in the passband, making the graph of the resulting frequency response smooth.

The second way to improve the properties of the frequency response is to divide the processing into several stages. For example, decimation is carried out not in one stage, but with the help of several links to lower the sampling frequency: R = R1 * R2 * ... Rn .

In order to save FPGA resources in some tasks it is possible to combine corrective and formative FIR filters. To do this, multiply their impulse responses or perform convolution of the spectra.

Result


For the convenience of calculating the filter-corrector, an m-script was written, which allows to get the result in visual form. The script can output the coefficients data in one of several popular formats, but if you wish, you can add and modify it to fit your goals.



To run the script, you need a CAD system Matlab or GNU Octave (I debugged in the latter). Next, the resulting coefficient file is loaded in * .COE format, into the Xilinx Core Generator, where a compensating FIR filter is implemented.



Schematic view of the FIR filter in the Xilinx Vivado environment (post-synthesis tab):



Alternative method


Another method for calculating corrective filters was suggested by my colleague - Antonov A.E. He wrote an interactive application that, step by step in manual mode, selects the required unevenness of the frequency response of the filter and unloads the coefficients for further work. The proposed program, c_koeff.exe, is designed to adjust the FIR filter coefficients behind the system of two CIC filters to compensate for the uneven frequency response of the entire system in the passband introduced by the CIC filters. It is assumed that the FIR filter coefficients are obtained in the FDATool environment of the MATLAB package and specified as a C-header file. The program is written in C ++ Builder. To display the calculated coefficients of the compensated FIR filter and its frequency response, an ISVI 6 or higher version program is used, which was developed by CJSC InSys and distributed free of charge . In order not to violate the rules of the resource, I will not advertise the achievements of the company and the features of the application software.

The result of the program is shown in the following figure. By iterating the parameter Np , we obtain the spectral function of the compensating filter. In the ISVI application, you can also observe the impulse response of the filter.


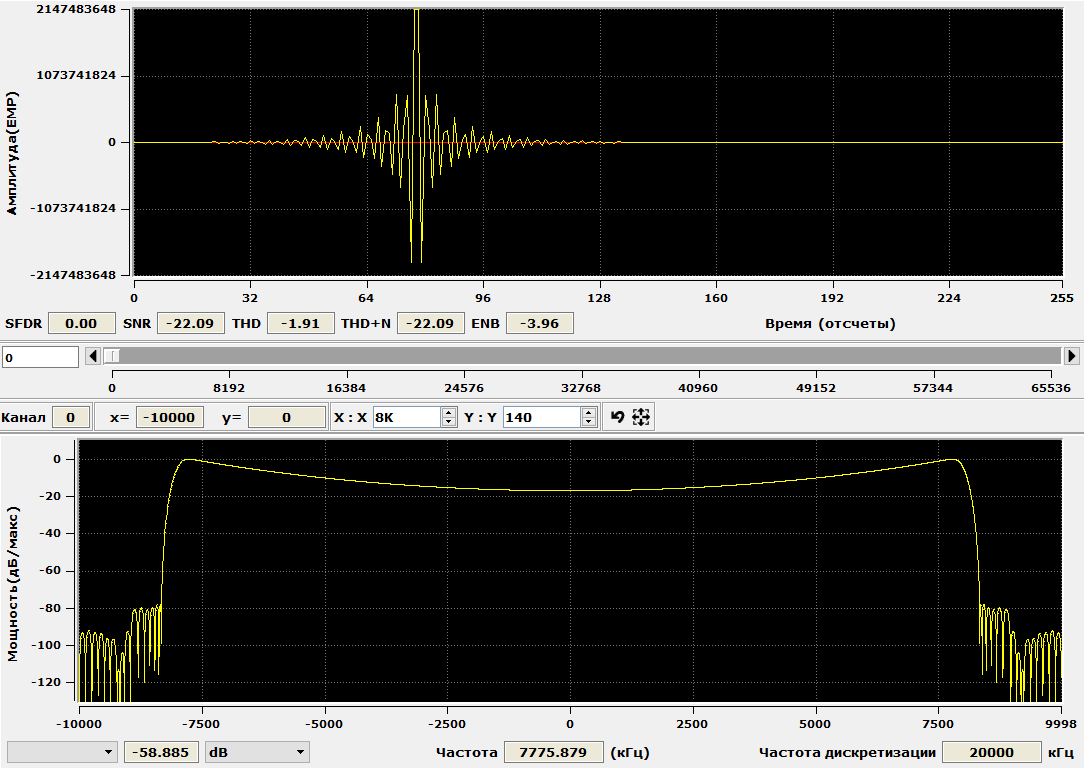
The application description is in the word-file among the sources on github (link below).

Source



Literature



Thanks for attention!

Source: https://habr.com/ru/post/324986/

More articles:


All Articles