Introduction to cryptography and encryption, part one. Lecture in Yandex
To understand the materials about the infrastructure of public keys, network security and HTTPS, you need to know the basics of cryptographic theory. One of the fastest ways to study them is to watch or give a lecture by Vladimir ivlad Ivanov. Vladimir is a well-known specialist in networks and their protection systems. He worked for a long time in Yandex, was one of the leaders of our operating department.
We publish this lecture for the first time along with the transcript. Let's start with the first part. Under the cut you will find the text and part of the slides.
I once read lectures on a crypt at MSU, and they took me half a year. I will try to tell you everything in two and a half hours. Never did it. Here we try.
')
Who understands what is DES? AES? Tls? Binominal mapping?
We will try to speak in general terms, because it is difficult and deep to disassemble will not work: there is little time and basic training must be quite large. We will operate with general concepts, rather superficially.
We will talk about what cryptographic primitives are, simple things from which you can later build more complex things, protocols.
We will talk about three primitives: symmetric encryption, message authentication, and asymmetric encryption. From them grows a lot of protocols.
Today we will try to talk a little bit about how keys are made. In general, let's talk about how to send a secure message using the crypto primitives that we have from one user to another.
When people talk about crypt in general, there are several fundamental principles. One of them is the Kirkoffs principle, which says that open source is very important in cryptography. More specifically, it gives a general knowledge of the protocol structure. The meaning is very simple: cryptographic algorithms that are used in a particular system should not be a secret to ensure its stability. Ideally, it is necessary to build systems so that their cryptographic side is completely known to the attacker and the only secret is the cryptographic key that is used in this system.
Modern and commercially available encryption systems — all or nearly all or the best of them — are built from components whose design and operation are well known. The only secret thing about them is the encryption key. There is only one significant exception known to me - a set of secret cryptographic protocols for all sorts of government organizations. In the USA, this is called the NSA suite B, and in Russia it is all sorts of strange, secret encryption algorithms that are used to a certain extent by military and government agencies.
I would not say that such algorithms are of great benefit to them, except that it is approximately like atomic physics. You can try on understanding the design of the protocol to understand the direction of thought of the people who developed it, and somehow overtake the other side. I don’t know how relevant such a principle is by today's standards, but people who know more about it than me do just that.
In every commercial protocol you come across, the situation is different. They use an open system everywhere, everyone adheres to this principle.
The first cryptographic primitive is symmetric ciphers.
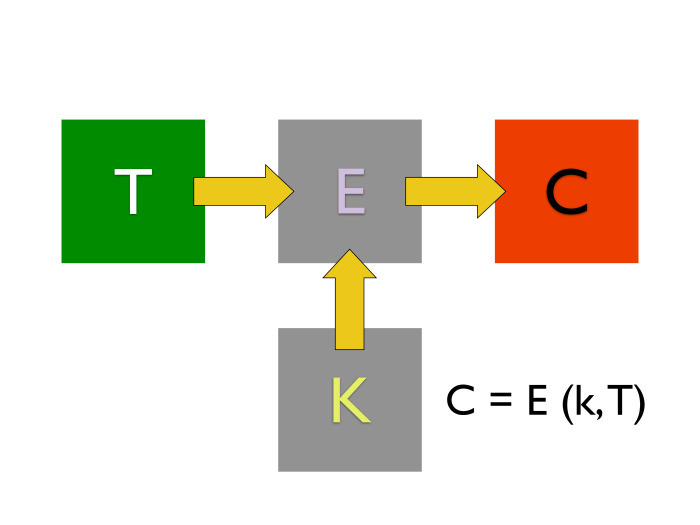
They are very simple. We have some kind of algorithm, at the input of which the plaintext goes and something called the key, some value. The output is an encrypted message. When we want to decrypt it, it is important that we take the same encryption key. And, applying it to another algorithm, the decryption algorithm, we get our plaintext back from the ciphertext.
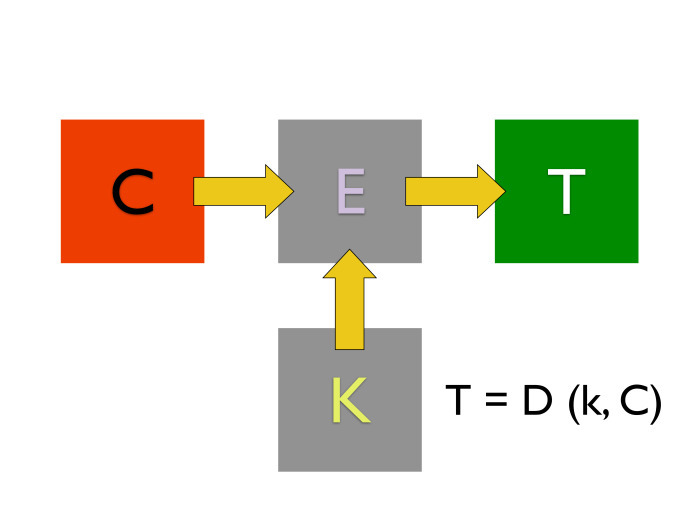
What are the important nuances here? In most common symmetric encryption algorithms that can be encountered, the size of the ciphertext is always equal to the size of the plaintext. Modern encryption algorithms operate on key sizes. The size of the keys is measured in bits. Modern size - from 128 to 256 bits for symmetric encryption algorithms. The rest, including the size of the block, we'll talk later.

Historically, in the conditional 4th century BC, there were two methods for the design of ciphers: substitution and permutation ciphers. Substitution ciphers are an algorithm, where in those days they replaced one letter of a message with another one according to some principle. A simple substitution cipher is according to the table: we take a table where it is written that we change A to I, B to U, etc. Then we encrypt this table, decipher it from it.
How do you think, in terms of key size, how complex is the algorithm? How many key options are there? The order factorial of the length of the alphabet. We take the table. How do we build it? Suppose there is a table of 26 characters. We can replace the letter A with any of them, the letter B with any of the remaining 25, C with any of the remaining 24 ... We get 26 * 25 * 24 * ... - that is, the factorial from 26. The factorial of the dimension of the alphabet.
If you take log 2 26 !, it will be a lot. I think you will definitely get around 100 bits of the key length, or even more. It turned out that from the point of view of the formal presentation of strength, the indicated encryption algorithm is quite good. 100 bits is acceptable. In this case, everyone, probably, in childhood or adolescence, when faced with encodings, saw that such algorithms are decrypted trivially. There are no problems with decoding.
For a long time there were all sorts of substitution algorithms in different constructions. One of them, even more primitive, is Caesar's cipher, where the table is formed not by random permutation of characters, but by a shift of three characters: A changes to D, B to E, etc. very easy: unlike tabular substitution, in the key of Caesar there are only 25 variants with 26 letters in the alphabet - not counting the trivial encryption of itself. And it is just possible to sort it out. There is some complexity here.
Why is the table substitution cipher so simple? Where does the problem arise from which we can easily, without even knowing anything about cryptography, decipher the table substitution? The point is frequency analysis. There are the most common letters - some kind of AND or E. Their prevalence is high, vowels are found much more often than consonants, and there are negative pairs that are never found in natural languages - something like b. I even gave students the task to make an automatic substitution cipher decoder, and, in principle, many coped.
What is the problem? It is necessary to distort the statistics of the distribution of letters, so that the common letters are not so shone in the encrypted text. The obvious way: let's encrypt the most common letters not in one character, but in five different, for example. If the letter is found on average five times more often, then let's take turns - first we will encrypt the first character, then the second, the third, and so on. Next, we will have a mapping of letters not 1 to 1, but, conditionally, 26 to 50. Statistics, therefore, will be violated. Before us is the first example of a polyalphabet cipher that somehow worked. However, there are quite a few problems with it, and most importantly, it is very inconvenient to work with the table.
We came up with the following: let's not encrypt with such tables, but try to take Caesar's cipher and change the shift for each next letter. The result is a Vigenere cipher.
Take as a key the word Vasya. Take the message MASHA. We engage Caesar's cipher, but counting from these letters. For example, B is the third letter in the alphabet. We must move the corresponding letter in the plaintext into three letters. M moves in P. A in A. Sh - by 16, by skipping the letter A, we obtain, conditionally, D. I will move A to I. FALL.
What is convenient in the resulting cipher? There were two identical letters, but as a result they were encrypted into different ones. This is great because it blurs statistics. The method worked well, until somewhere in the XIX century, literally recently against the background of the history of cryptography, they did not figure out how to break it. If you look at a message of several dozen words, and the key is rather short, the whole construction looks like several Caesar ciphers. We say: OK, let's look at every fourth letter — first, fifth, ninth — as Caesar's cipher. And we will look for statistical laws among them. We will find them. Then take the second, sixth, tenth, and so on. Find again. This will restore the key. The only problem is to understand how long it is. It is not very difficult, well, how long can it be? Well, 4, well, 10 characters. Going through 6 options from 4 to 10 is not very difficult. A simple attack - it was available without computers, just at the expense of a pen and a sheet of paper.
How to make an unbreakable cipher out of this thing? Take the key text size. A character named Claude Shannon in the twentieth century, in 1946, wrote the classic first work on cryptography as a section of mathematics, where he formulated a theorem. The key length is equal to the length of the message — it used XOR instead of adding modulo the length of the alphabet, but in this situation it is not very important. The key is generated randomly, is a sequence of random bits, and the output will also result in a random sequence of bits. Theorem: if we have such a key, then such a construction is absolutely stable. The proof is not very complicated, but now I will not talk about him.
It is important that you can create an unbreakable cipher, but it has flaws. First, the key must be completely random. Secondly, it should never be reused. Third, the key length must be equal to the message length. Why can not I use the same key to encrypt different messages? Because, having intercepted this key next time, it will be possible to decrypt all messages? Not. Will Caesar's cipher appear in the first characters? Not really understood. It seems not.
Take two messages: MASHA, encrypted with the VASYA key, and another word that also had the VASY key, FAITH. We get something like this: ZEZHYA. Fold the two received messages, and so that the two keys are mutually deleted. As a result, we obtain only the difference between a meaningful ciphertext and a meaningful ciphertext. On the XOR, this is done more conveniently than on addition along the length of the alphabet, but there is practically no difference.
If we get the difference between two meaningful ciphertexts, then further, as a rule, it becomes much easier, since natural language texts have high redundancy. Often we can guess what is happening, making different assumptions, hypotheses. And most importantly, each correct hypothesis will reveal to us a piece of the key, and therefore pieces of two ciphertexts. Something like this. Therefore bad.
In addition to the substitution ciphers, there were also permutation ciphers. With them, too, everything is quite simple. We take the message of VASIAI, write it into a block of some length, for example, a BID, and read the result in the same way.
God knows what a thing. How to break it is also understandable - let's look through all possible permutations. There are not many of them here. We take the length of the block, select and restore.
As the next iteration, the following method was chosen: let's take the same thing, and from the top we will write some key - SIMON. Rearrange the columns so that the letters are in alphabetical order. As a result, we obtain a new permutation by key. It is already much better than the old one, since the number of permutations is much larger and it is not always easy to pick it up.
Each modern cipher in one way or another is based on these two principles - substitution and permutation. Now their use is much more complicated, but the basic principles themselves remain the same.

If we talk about modern ciphers, they are divided into two categories: flow and block. The stream cipher is designed in such a way that it actually represents a random number generator, the output of which we add modulo 2, “Xori,” with our ciphertext, as I can see on the slide. I said earlier: if the length of the resulting keystream — the key itself — is absolutely random, never reused, and its length is equal to the length of the message, then we have an absolutely strong cipher that cannot be broken.
The question arises: how to generate a random, long and eternal Key for such a cipher? How do stream ciphers work at all? In fact, they are a random number generator based on some initial value. The initial value is the cipher key, the answer.
There is one amusing exception to this story - the cipher block. This is a real spy story about real espionage. Some people who need absolutely stable communication generate random numbers — for example, by literally throwing a die or literally pulling the balls out of the drum, like in a lotto. Create two sheets where these random numbers are printed. One sheet is given to the recipient, and the second is left at the sender. If they want to chat, they use this stream of random numbers as a key stream. No, the story is not taken from the very distant past. I have a real radio interception from October 15, 2014: 7 2 6, 7 2 6, 7 2 6. This is a call sign. 4 8 3, 4 8 3, 4 8 3. This is a cipher block number. 5 0, 5 0, 5 0. This is the number of words. 8 4 4 7 9 8 4 4 7 9 2 0 5 1 4 2 0 5 1 4, etc. 50 such numerical groups. I don’t know where, somewhere in Russia, there was a man with a pen and a pencil at an ordinary radio receiver and wrote down these numbers. Writing them down, he took out a similar thing, folded them modulo 10, and received his message. In other words, it really works, and such a message cannot be cracked. If really random random numbers were actually generated and he subsequently burned a piece of paper with a key, then there is no way to hack it, absolutely.
But there are quite a few problems. The first is how to generate really good random numbers. The world around us is deterministic, and if we are talking about computers, they are fully determined.
Secondly, delivering keys of this size ... if we are talking about the transfer of messages from 55 digital groups, then it is not very difficult to do this, but transferring several gigabytes of text is already a serious problem. Therefore, we need some algorithms that, in essence, generate pseudo-random numbers based on some small initial value and which could be used as such streaming algorithms.
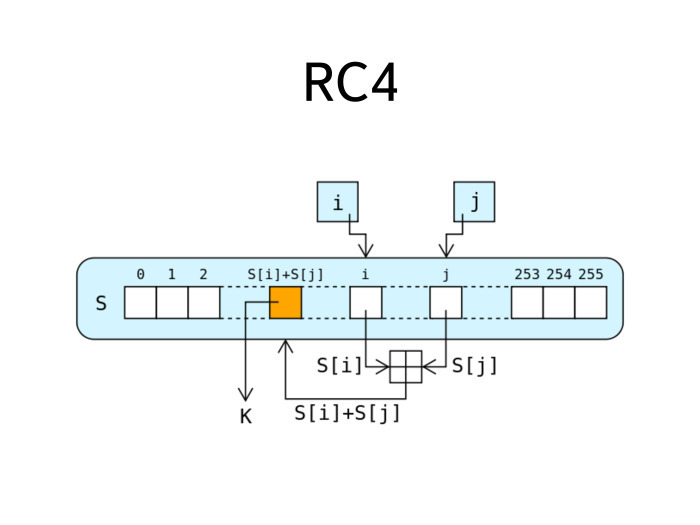
The most historically common algorithm of this kind is called RC4. It was developed by Ron Rivest about 25 years ago and was actively used for a very long time, it was the most common algorithm for TLS, all its various options, including HTTPS. But lately RC4 has begun to show its age. For him, there are a number of attacks. It is actively used in WEP. There was one good lecture by Anton , a story that shows: the poor use of a decent encryption algorithm even by today's standards leads to compromising the whole system.
RC4 is made easy. The slide describes his work entirely. There is an internal byte state of 256 bytes. At each step of this state there are two numbers, two pointers to different bytes in the state. And at each step there is an addition between these numbers - they are placed in some place of the state. The byte received from there is the next byte in the numerical sequence. Rotating this knob in this way, performing a similar action at each step, we get every next byte. We can get the next byte of a numeric sequence forever, in a stream.
The big advantage of RC4 is that it is entirely intrabyte, which means that its software implementation runs fairly quickly - much faster, at times, if not tens of times faster than the DES code that was comparable to it at about the same time as it. Therefore, RC4 and received such a distribution. For a long time he was a commercial secret of RSA, but then, somewhere around the 90s, some people anonymously published the sources of his device on the cypherpunks mailing list. As a result, a lot of drama arose, there were cries, they say, how is it that some indecent people stole the intellectual property of RSA and published it. RSA began to threaten all patents, all sorts of legal prosecutions. To avoid them, all implementations of the algorithm that are in the open source are called not RC4, but ARC4 or ARCFOUR. And - alleged. This is a cipher, which on all test cases coincides with RC4, but technically it is not like them.
If you are configuring some SSH or OpenSSL, you will not find any mention of RC4 in it, but you will find ARC4 or something like that. A simple construction, it is already old, there are attacks on it now, and it is not highly recommended for use.
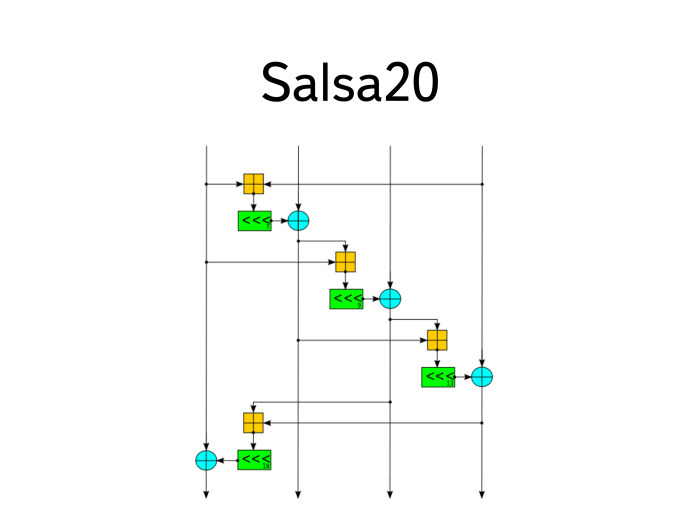
There have been several attempts to replace him. Probably, in my biased opinion, the Salsa20 cipher and several of its followers from Dan Bershtein, a character well-known in narrow circles, became the most successful. The linuxoid is commonly known as the author of qmail.
Salsa20 is more complex than DES. His block diagram is complicated, but he has several interesting and cool features. For a start, it is always executed in a finite time, each round, which is important for protection against timing attacks. These are such attacks, where the attacker observes the behavior of the encryption system, feeding it different ciphertexts or different keys behind this black box. And, understanding the changes in response time or in the power consumption of the system, he can draw conclusions about exactly what processes took place inside. If you think that the attack is highly contrived, it is not. Attacks of this kind on smart cards are very widespread - very convenient, since the attacker has full access to the box. The only thing that he, as a rule, cannot do in it is to read the key itself. It is difficult, and he can do everything else - to send different messages there and try to decipher them.
Salsa20 is designed so that it is always performed in constant constant time. : , 2 32, 32- . Salsa20 , RC4. — cipher suite TLS, Salsa20, — . eSTREAM . , Salsa — . -. , — , — cipher suite TLS Salsa20. .
, . , , 2 64 . . , , .
? , , . , . — . , , . .
, , , 10 , 1 , 10 . .
Salsa , , . 20 . 20 — 512 .
— 8 . 256-, 8 — 250 251 . , , . . , , .
. , . , .
? : , Salsa, , , . . .
, — .
, . . , - .
. -. , , — . , , .
— , 128 . , , 128 256 , . — , : 128 256 , .
— DES AES. DES , RC4. DES — 64 , — 56 . IBM . IBM , 128 . , 124 192 .
DES , . 64 56 .
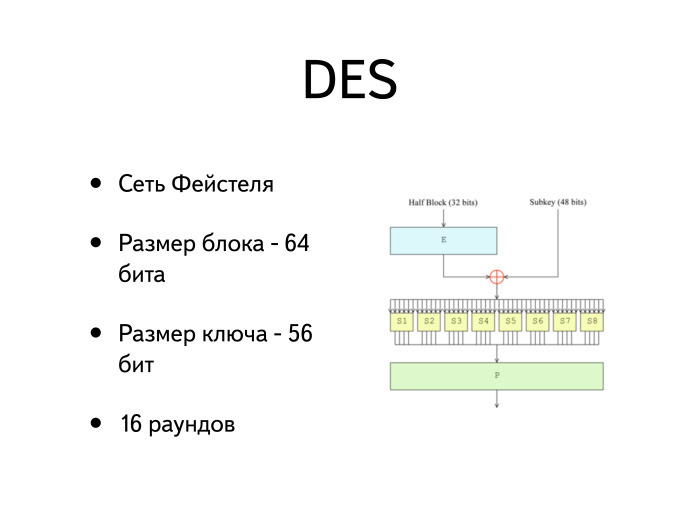
20 . — , , , . DES , , .
. . , . , 56 .
DES? , . . , , : . . , . .
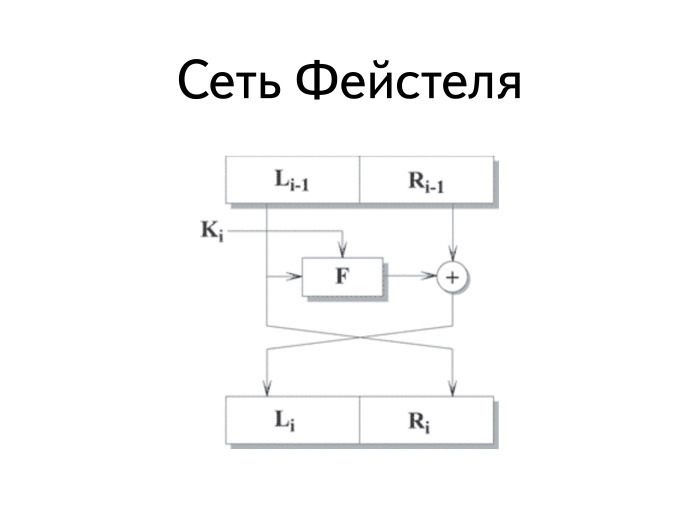
. : F . , . .
: , . , .
? 30 , . , .
— , 16 . 16 16 , F.
— - . : 32 , , 32 . 32 , 48: , .
, — 48 , 48- .
, S- . , 48 32 .
, P. 32 . , .
S-: 6 4. , , XOR . S- , DES . , , . DES : .
S-, . , . , 10 , DES , — . : — , , 0 1 — , . , 0 1 . , DES, , , . : , 10 , , .
S- . , : S-. , .
56 — , . . ?
: . Triple DES. : , . .
, . , k1 k2 k3, . , DES . , .
, 56 . — k1 k2. 56 + 56 = 112 . 112 — . , 100 . , 112 ?
DES 16 . 16 . 16 . — . , k3, , k1 k2.
. - , . , 2 56 . - . 2 56 — — k1 k2, .
— 112 , 57, . , . — , : k1, k2, k3. Triple DES. -. DES — , : , — .
Triple DES DES. .
DES? . TLS, cipher suite TLS, Triple DES DES. , . .
, , . , , . , , PIN, — . , PIN, PIN-. — , DES. , , Triple DES, DES.
DES , , . , NIST, : . AES.
DES digital encrypted standard. AES — advanced encrypted standard. AES — 128 , 64. . AES — 128, 192 256 . AES , , . 128 10 , 256 — 14.
, . — .
DES, AES . . AES , DES. 128- , 10 10 . , DES, .
. — .
AES 4 4. — . 16 128 . AES .
— .
, . 4 4. , 1 , — 2 , — 3, .
. . , . .
, — XOR . .
, . :
, . .
4 10 , 128- 128- .
AES? , , DES. AES . AES DES , AES , .
, Intel AMD, AES , . — AES . DES , , 1-2 , 10- AES- .
. 128 64 128 64 .
, , 16 ?
, , — , , , , .
, , 16 . ECB — electronic code boot, 16 AES 8 DES .
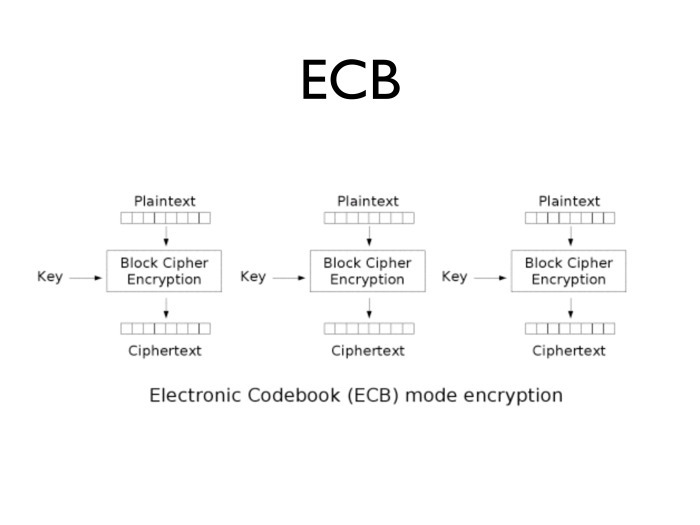
, , .

, ECB. , , , . What is the problem? , . , — .
- , , — , . CBC.
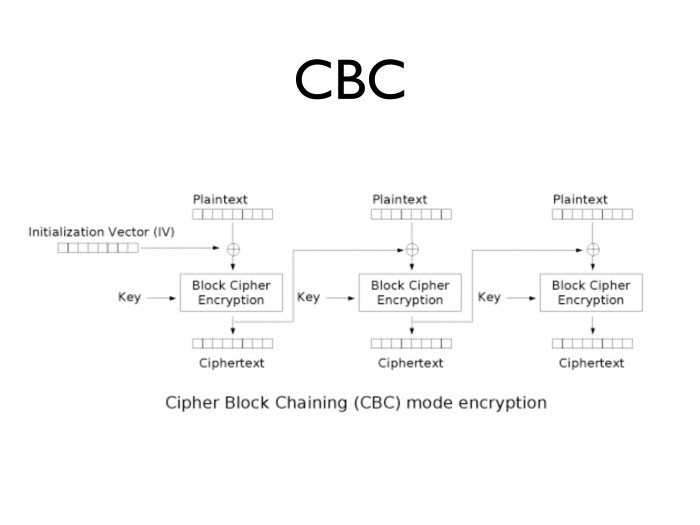
, , . . .
, 2 . — . 2 . — . 2 . . : .
, , , , . . .
CBC .
. : , , DES. DES , DES 64 . , 64 ? 1/(2 64 ). ? .
We publish this lecture for the first time along with the transcript. Let's start with the first part. Under the cut you will find the text and part of the slides.
I once read lectures on a crypt at MSU, and they took me half a year. I will try to tell you everything in two and a half hours. Never did it. Here we try.
')
Who understands what is DES? AES? Tls? Binominal mapping?
We will try to speak in general terms, because it is difficult and deep to disassemble will not work: there is little time and basic training must be quite large. We will operate with general concepts, rather superficially.
We will talk about what cryptographic primitives are, simple things from which you can later build more complex things, protocols.
We will talk about three primitives: symmetric encryption, message authentication, and asymmetric encryption. From them grows a lot of protocols.
Today we will try to talk a little bit about how keys are made. In general, let's talk about how to send a secure message using the crypto primitives that we have from one user to another.
When people talk about crypt in general, there are several fundamental principles. One of them is the Kirkoffs principle, which says that open source is very important in cryptography. More specifically, it gives a general knowledge of the protocol structure. The meaning is very simple: cryptographic algorithms that are used in a particular system should not be a secret to ensure its stability. Ideally, it is necessary to build systems so that their cryptographic side is completely known to the attacker and the only secret is the cryptographic key that is used in this system.
Modern and commercially available encryption systems — all or nearly all or the best of them — are built from components whose design and operation are well known. The only secret thing about them is the encryption key. There is only one significant exception known to me - a set of secret cryptographic protocols for all sorts of government organizations. In the USA, this is called the NSA suite B, and in Russia it is all sorts of strange, secret encryption algorithms that are used to a certain extent by military and government agencies.
I would not say that such algorithms are of great benefit to them, except that it is approximately like atomic physics. You can try on understanding the design of the protocol to understand the direction of thought of the people who developed it, and somehow overtake the other side. I don’t know how relevant such a principle is by today's standards, but people who know more about it than me do just that.
In every commercial protocol you come across, the situation is different. They use an open system everywhere, everyone adheres to this principle.
The first cryptographic primitive is symmetric ciphers.

They are very simple. We have some kind of algorithm, at the input of which the plaintext goes and something called the key, some value. The output is an encrypted message. When we want to decrypt it, it is important that we take the same encryption key. And, applying it to another algorithm, the decryption algorithm, we get our plaintext back from the ciphertext.

What are the important nuances here? In most common symmetric encryption algorithms that can be encountered, the size of the ciphertext is always equal to the size of the plaintext. Modern encryption algorithms operate on key sizes. The size of the keys is measured in bits. Modern size - from 128 to 256 bits for symmetric encryption algorithms. The rest, including the size of the block, we'll talk later.

Historically, in the conditional 4th century BC, there were two methods for the design of ciphers: substitution and permutation ciphers. Substitution ciphers are an algorithm, where in those days they replaced one letter of a message with another one according to some principle. A simple substitution cipher is according to the table: we take a table where it is written that we change A to I, B to U, etc. Then we encrypt this table, decipher it from it.
How do you think, in terms of key size, how complex is the algorithm? How many key options are there? The order factorial of the length of the alphabet. We take the table. How do we build it? Suppose there is a table of 26 characters. We can replace the letter A with any of them, the letter B with any of the remaining 25, C with any of the remaining 24 ... We get 26 * 25 * 24 * ... - that is, the factorial from 26. The factorial of the dimension of the alphabet.
If you take log 2 26 !, it will be a lot. I think you will definitely get around 100 bits of the key length, or even more. It turned out that from the point of view of the formal presentation of strength, the indicated encryption algorithm is quite good. 100 bits is acceptable. In this case, everyone, probably, in childhood or adolescence, when faced with encodings, saw that such algorithms are decrypted trivially. There are no problems with decoding.
For a long time there were all sorts of substitution algorithms in different constructions. One of them, even more primitive, is Caesar's cipher, where the table is formed not by random permutation of characters, but by a shift of three characters: A changes to D, B to E, etc. very easy: unlike tabular substitution, in the key of Caesar there are only 25 variants with 26 letters in the alphabet - not counting the trivial encryption of itself. And it is just possible to sort it out. There is some complexity here.
Why is the table substitution cipher so simple? Where does the problem arise from which we can easily, without even knowing anything about cryptography, decipher the table substitution? The point is frequency analysis. There are the most common letters - some kind of AND or E. Their prevalence is high, vowels are found much more often than consonants, and there are negative pairs that are never found in natural languages - something like b. I even gave students the task to make an automatic substitution cipher decoder, and, in principle, many coped.
What is the problem? It is necessary to distort the statistics of the distribution of letters, so that the common letters are not so shone in the encrypted text. The obvious way: let's encrypt the most common letters not in one character, but in five different, for example. If the letter is found on average five times more often, then let's take turns - first we will encrypt the first character, then the second, the third, and so on. Next, we will have a mapping of letters not 1 to 1, but, conditionally, 26 to 50. Statistics, therefore, will be violated. Before us is the first example of a polyalphabet cipher that somehow worked. However, there are quite a few problems with it, and most importantly, it is very inconvenient to work with the table.
We came up with the following: let's not encrypt with such tables, but try to take Caesar's cipher and change the shift for each next letter. The result is a Vigenere cipher.
Take as a key the word Vasya. Take the message MASHA. We engage Caesar's cipher, but counting from these letters. For example, B is the third letter in the alphabet. We must move the corresponding letter in the plaintext into three letters. M moves in P. A in A. Sh - by 16, by skipping the letter A, we obtain, conditionally, D. I will move A to I. FALL.
What is convenient in the resulting cipher? There were two identical letters, but as a result they were encrypted into different ones. This is great because it blurs statistics. The method worked well, until somewhere in the XIX century, literally recently against the background of the history of cryptography, they did not figure out how to break it. If you look at a message of several dozen words, and the key is rather short, the whole construction looks like several Caesar ciphers. We say: OK, let's look at every fourth letter — first, fifth, ninth — as Caesar's cipher. And we will look for statistical laws among them. We will find them. Then take the second, sixth, tenth, and so on. Find again. This will restore the key. The only problem is to understand how long it is. It is not very difficult, well, how long can it be? Well, 4, well, 10 characters. Going through 6 options from 4 to 10 is not very difficult. A simple attack - it was available without computers, just at the expense of a pen and a sheet of paper.
How to make an unbreakable cipher out of this thing? Take the key text size. A character named Claude Shannon in the twentieth century, in 1946, wrote the classic first work on cryptography as a section of mathematics, where he formulated a theorem. The key length is equal to the length of the message — it used XOR instead of adding modulo the length of the alphabet, but in this situation it is not very important. The key is generated randomly, is a sequence of random bits, and the output will also result in a random sequence of bits. Theorem: if we have such a key, then such a construction is absolutely stable. The proof is not very complicated, but now I will not talk about him.
It is important that you can create an unbreakable cipher, but it has flaws. First, the key must be completely random. Secondly, it should never be reused. Third, the key length must be equal to the message length. Why can not I use the same key to encrypt different messages? Because, having intercepted this key next time, it will be possible to decrypt all messages? Not. Will Caesar's cipher appear in the first characters? Not really understood. It seems not.
Take two messages: MASHA, encrypted with the VASYA key, and another word that also had the VASY key, FAITH. We get something like this: ZEZHYA. Fold the two received messages, and so that the two keys are mutually deleted. As a result, we obtain only the difference between a meaningful ciphertext and a meaningful ciphertext. On the XOR, this is done more conveniently than on addition along the length of the alphabet, but there is practically no difference.
If we get the difference between two meaningful ciphertexts, then further, as a rule, it becomes much easier, since natural language texts have high redundancy. Often we can guess what is happening, making different assumptions, hypotheses. And most importantly, each correct hypothesis will reveal to us a piece of the key, and therefore pieces of two ciphertexts. Something like this. Therefore bad.
In addition to the substitution ciphers, there were also permutation ciphers. With them, too, everything is quite simple. We take the message of VASIAI, write it into a block of some length, for example, a BID, and read the result in the same way.
God knows what a thing. How to break it is also understandable - let's look through all possible permutations. There are not many of them here. We take the length of the block, select and restore.
As the next iteration, the following method was chosen: let's take the same thing, and from the top we will write some key - SIMON. Rearrange the columns so that the letters are in alphabetical order. As a result, we obtain a new permutation by key. It is already much better than the old one, since the number of permutations is much larger and it is not always easy to pick it up.
Each modern cipher in one way or another is based on these two principles - substitution and permutation. Now their use is much more complicated, but the basic principles themselves remain the same.

If we talk about modern ciphers, they are divided into two categories: flow and block. The stream cipher is designed in such a way that it actually represents a random number generator, the output of which we add modulo 2, “Xori,” with our ciphertext, as I can see on the slide. I said earlier: if the length of the resulting keystream — the key itself — is absolutely random, never reused, and its length is equal to the length of the message, then we have an absolutely strong cipher that cannot be broken.
The question arises: how to generate a random, long and eternal Key for such a cipher? How do stream ciphers work at all? In fact, they are a random number generator based on some initial value. The initial value is the cipher key, the answer.
There is one amusing exception to this story - the cipher block. This is a real spy story about real espionage. Some people who need absolutely stable communication generate random numbers — for example, by literally throwing a die or literally pulling the balls out of the drum, like in a lotto. Create two sheets where these random numbers are printed. One sheet is given to the recipient, and the second is left at the sender. If they want to chat, they use this stream of random numbers as a key stream. No, the story is not taken from the very distant past. I have a real radio interception from October 15, 2014: 7 2 6, 7 2 6, 7 2 6. This is a call sign. 4 8 3, 4 8 3, 4 8 3. This is a cipher block number. 5 0, 5 0, 5 0. This is the number of words. 8 4 4 7 9 8 4 4 7 9 2 0 5 1 4 2 0 5 1 4, etc. 50 such numerical groups. I don’t know where, somewhere in Russia, there was a man with a pen and a pencil at an ordinary radio receiver and wrote down these numbers. Writing them down, he took out a similar thing, folded them modulo 10, and received his message. In other words, it really works, and such a message cannot be cracked. If really random random numbers were actually generated and he subsequently burned a piece of paper with a key, then there is no way to hack it, absolutely.
But there are quite a few problems. The first is how to generate really good random numbers. The world around us is deterministic, and if we are talking about computers, they are fully determined.
Secondly, delivering keys of this size ... if we are talking about the transfer of messages from 55 digital groups, then it is not very difficult to do this, but transferring several gigabytes of text is already a serious problem. Therefore, we need some algorithms that, in essence, generate pseudo-random numbers based on some small initial value and which could be used as such streaming algorithms.

The most historically common algorithm of this kind is called RC4. It was developed by Ron Rivest about 25 years ago and was actively used for a very long time, it was the most common algorithm for TLS, all its various options, including HTTPS. But lately RC4 has begun to show its age. For him, there are a number of attacks. It is actively used in WEP. There was one good lecture by Anton , a story that shows: the poor use of a decent encryption algorithm even by today's standards leads to compromising the whole system.
RC4 is made easy. The slide describes his work entirely. There is an internal byte state of 256 bytes. At each step of this state there are two numbers, two pointers to different bytes in the state. And at each step there is an addition between these numbers - they are placed in some place of the state. The byte received from there is the next byte in the numerical sequence. Rotating this knob in this way, performing a similar action at each step, we get every next byte. We can get the next byte of a numeric sequence forever, in a stream.
The big advantage of RC4 is that it is entirely intrabyte, which means that its software implementation runs fairly quickly - much faster, at times, if not tens of times faster than the DES code that was comparable to it at about the same time as it. Therefore, RC4 and received such a distribution. For a long time he was a commercial secret of RSA, but then, somewhere around the 90s, some people anonymously published the sources of his device on the cypherpunks mailing list. As a result, a lot of drama arose, there were cries, they say, how is it that some indecent people stole the intellectual property of RSA and published it. RSA began to threaten all patents, all sorts of legal prosecutions. To avoid them, all implementations of the algorithm that are in the open source are called not RC4, but ARC4 or ARCFOUR. And - alleged. This is a cipher, which on all test cases coincides with RC4, but technically it is not like them.
If you are configuring some SSH or OpenSSL, you will not find any mention of RC4 in it, but you will find ARC4 or something like that. A simple construction, it is already old, there are attacks on it now, and it is not highly recommended for use.

There have been several attempts to replace him. Probably, in my biased opinion, the Salsa20 cipher and several of its followers from Dan Bershtein, a character well-known in narrow circles, became the most successful. The linuxoid is commonly known as the author of qmail.
Salsa20 is more complex than DES. His block diagram is complicated, but he has several interesting and cool features. For a start, it is always executed in a finite time, each round, which is important for protection against timing attacks. These are such attacks, where the attacker observes the behavior of the encryption system, feeding it different ciphertexts or different keys behind this black box. And, understanding the changes in response time or in the power consumption of the system, he can draw conclusions about exactly what processes took place inside. If you think that the attack is highly contrived, it is not. Attacks of this kind on smart cards are very widespread - very convenient, since the attacker has full access to the box. The only thing that he, as a rule, cannot do in it is to read the key itself. It is difficult, and he can do everything else - to send different messages there and try to decipher them.
Salsa20 is designed so that it is always performed in constant constant time. : , 2 32, 32- . Salsa20 , RC4. — cipher suite TLS, Salsa20, — . eSTREAM . , Salsa — . -. , — , — cipher suite TLS Salsa20. .
, . , , 2 64 . . , , .
? , , . , . — . , , . .
, , , 10 , 1 , 10 . .
Salsa , , . 20 . 20 — 512 .
— 8 . 256-, 8 — 250 251 . , , . . , , .
. , . , .
? : , Salsa, , , . . .
, — .
, . . , - .
. -. , , — . , , .
— , 128 . , , 128 256 , . — , : 128 256 , .
— DES AES. DES , RC4. DES — 64 , — 56 . IBM . IBM , 128 . , 124 192 .
DES , . 64 56 .

20 . — , , , . DES , , .
. . , . , 56 .
DES? , . . , , : . . , . .

. : F . , . .
: , . , .
? 30 , . , .
— , 16 . 16 16 , F.
— - . : 32 , , 32 . 32 , 48: , .
, — 48 , 48- .
, S- . , 48 32 .
, P. 32 . , .
S-: 6 4. , , XOR . S- , DES . , , . DES : .
S-, . , . , 10 , DES , — . : — , , 0 1 — , . , 0 1 . , DES, , , . : , 10 , , .
S- . , : S-. , .
56 — , . . ?
: . Triple DES. : , . .
, . , k1 k2 k3, . , DES . , .
, 56 . — k1 k2. 56 + 56 = 112 . 112 — . , 100 . , 112 ?
DES 16 . 16 . 16 . — . , k3, , k1 k2.
. - , . , 2 56 . - . 2 56 — — k1 k2, .
— 112 , 57, . , . — , : k1, k2, k3. Triple DES. -. DES — , : , — .
Triple DES DES. .
DES? . TLS, cipher suite TLS, Triple DES DES. , . .
, , . , , . , , PIN, — . , PIN, PIN-. — , DES. , , Triple DES, DES.
DES , , . , NIST, : . AES.
DES digital encrypted standard. AES — advanced encrypted standard. AES — 128 , 64. . AES — 128, 192 256 . AES , , . 128 10 , 256 — 14.
, . — .
DES, AES . . AES , DES. 128- , 10 10 . , DES, .
. — .
AES 4 4. — . 16 128 . AES .
— .
, . 4 4. , 1 , — 2 , — 3, .
. . , . .
, — XOR . .
, . :
, . .
4 10 , 128- 128- .
AES? , , DES. AES . AES DES , AES , .
, Intel AMD, AES , . — AES . DES , , 1-2 , 10- AES- .
. 128 64 128 64 .
, , 16 ?
, , — , , , , .
, , 16 . ECB — electronic code boot, 16 AES 8 DES .

, , .

, ECB. , , , . What is the problem? , . , — .
- , , — , . CBC.

, , . . .
, 2 . — . 2 . — . 2 . . : .
, , , , . . .
CBC .
. : , , DES. DES , DES 64 . , 64 ? 1/(2 64 ). ? .
Source: https://habr.com/ru/post/324866/
All Articles